MOMENT KURTOSIS DAN SKEWNESS Misalkan X 1 X

MOMENT, KURTOSIS DAN SKEWNESS Misalkan X 1, X 2, . . . , Xn merupakan nilai dari variabel X. Kuantitas: disebut moment ke r dari X. Untuk r =1, menjadi rerata aritmatika. Moment ke r disekitar rerata Diperhatikan m 1=0 dan m 2= s 2 variansi. didefisikan sbg:

CONTOH: Tentukan moment pertama, kedua, ketiga dan kempat dari 2, 3, 7, 8, 10. PENYELESAIAN: a. moment pertama: b. moment kedua: c. moment ketiga: d. moment kempat:

Moment di sekitar A. dimana adalah deviasi X thd A. CONTOH: Diberikan data 2, 3, 7, 8, 10. Empat moment pertama di sekitar 4 adalah:

MOMENT DATA KELOMPOK Misalkan X 1, X 2, . . . , Xn terjadi dengan frekuensi f 1, f 2, . . . , f n.

HUBUNGAN ANTAR MOMENT Misalkan mr moment disekitar titik sebarang dan mr’ moment di sekitar rerata maka berlaku hb: Bukti: lihat prob. 5. 5. METODA KODING:

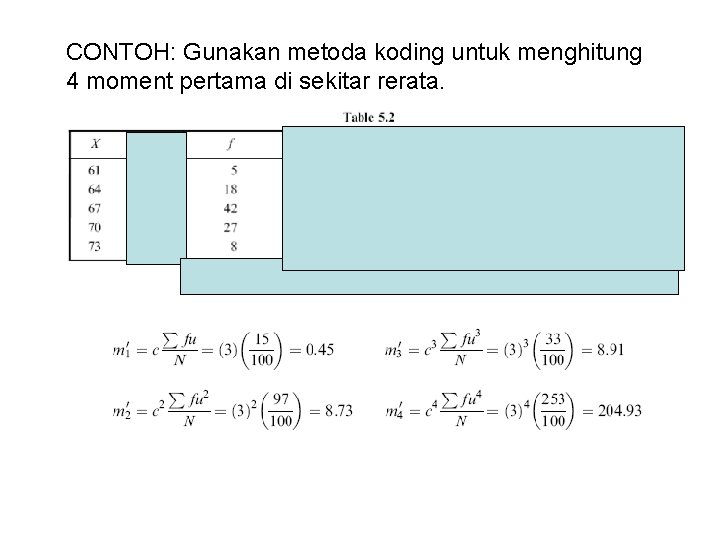
CONTOH: Gunakan metoda koding untuk menghitung 4 moment pertama di sekitar rerata.

Dengan menggunakan hb antar moment diperoleh:

SKEWNESS Skewness: ukuran ketidaksimetrisan (kemen-cengan) distribusi. Distribusi yang ekor kurvanya lebih panjang kekanan disebut menceng kekanan atau positive skewness. Begitu juga sebaliknya.

KOEF. SKEWNESS • Koef. Pearson I: • Koef. Pearson II: Diperhatikan bila distribusinya normal maka koefisien skewness bernilai nol. Koefisien skewness lainnya: • koef. kuartil skewness: • koef. skewness 10 -90% percentile: • koef. moment skewness:

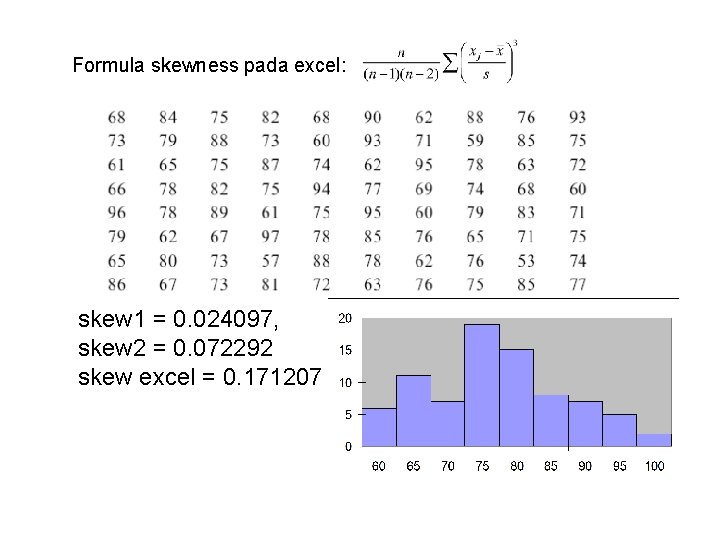
Formula skewness pada excel: skew 1 = 0. 024097, skew 2 = 0. 072292 skew excel = 0. 171207

KURTOSIS • Ukuran kelancipan distribusi data dimana distribusi normal sbg pembanding. • Macam-macam ukuran kurtosis: – koef. moment kurtosis: – kurtosis thd kuartil dan percentil: – pada excel: – kurtosis positif distribusi lancip – kurtosis negatif distribusi tumpul