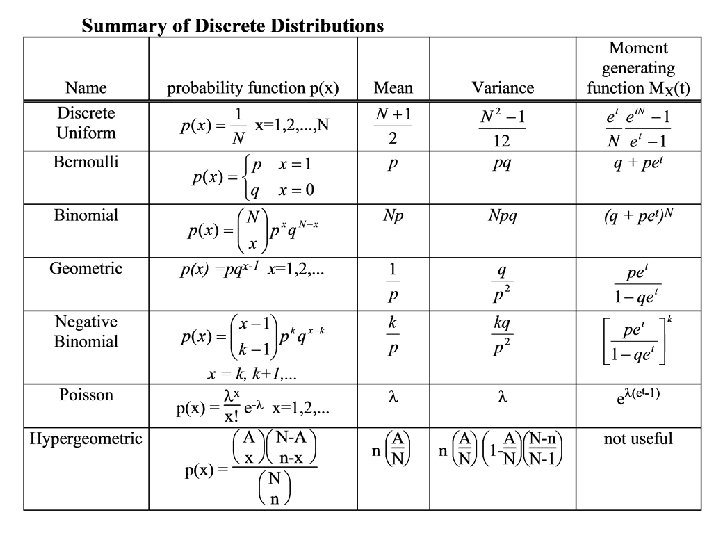
Moment Generating Functions Continuous Distributions The Uniform distribution

Moment Generating Functions

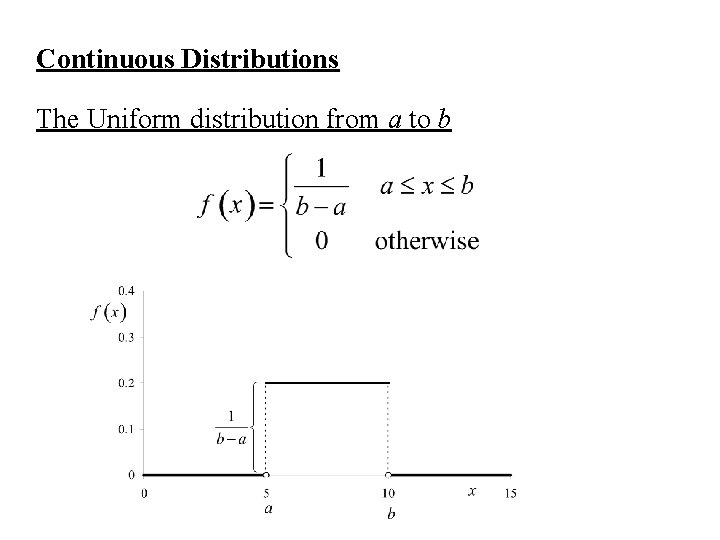
Continuous Distributions The Uniform distribution from a to b

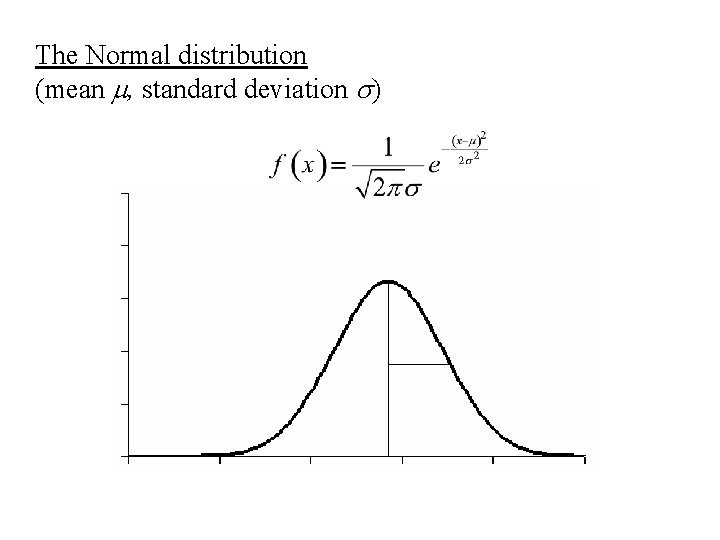
The Normal distribution (mean m, standard deviation s)

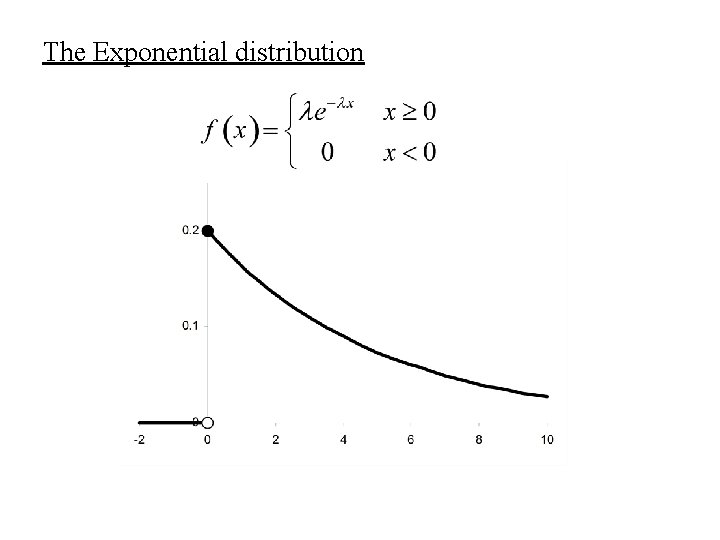
The Exponential distribution

Weibull distribution with parameters a and b.

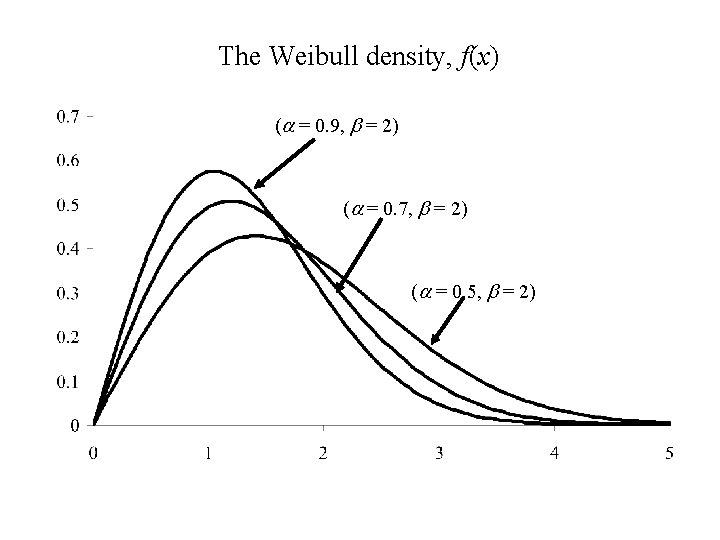
The Weibull density, f(x) (a = 0. 9, b = 2) (a = 0. 7, b = 2) (a = 0. 5, b = 2)

The Gamma distribution Let the continuous random variable X have density function: Then X is said to have a Gamma distribution with parameters a and l.

Expectation of functions of Random Variables

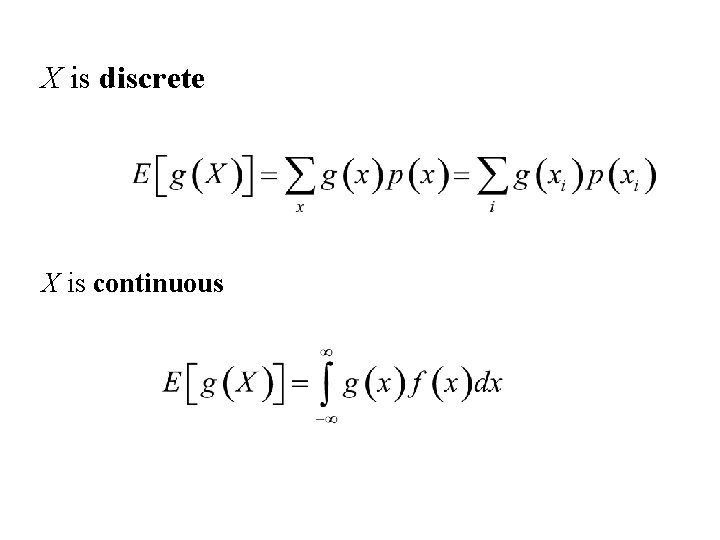
X is discrete X is continuous

Moments of Random Variables

The kth moment of X.

the kth central moment of X where m = m 1 = E(X) = the first moment of X.

Rules for expectation

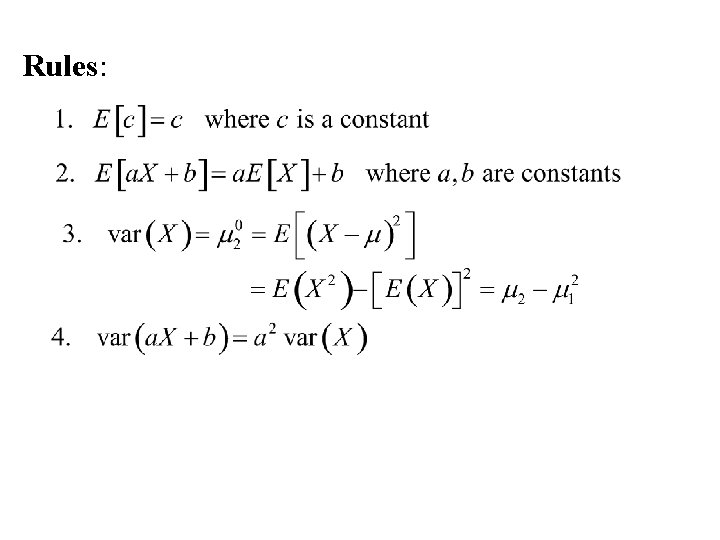
Rules:

Moment generating functions

Moment Generating function of a R. V. X

Examples 1. The Binomial distribution (parameters p, n)

2. The Poisson distribution (parameter l) The moment generating function of X , m. X(t) is:

3. The Exponential distribution (parameter l) The moment generating function of X , m. X(t) is:

4. The Standard Normal distribution (m = 0, s = 1) The moment generating function of X , m. X(t) is:

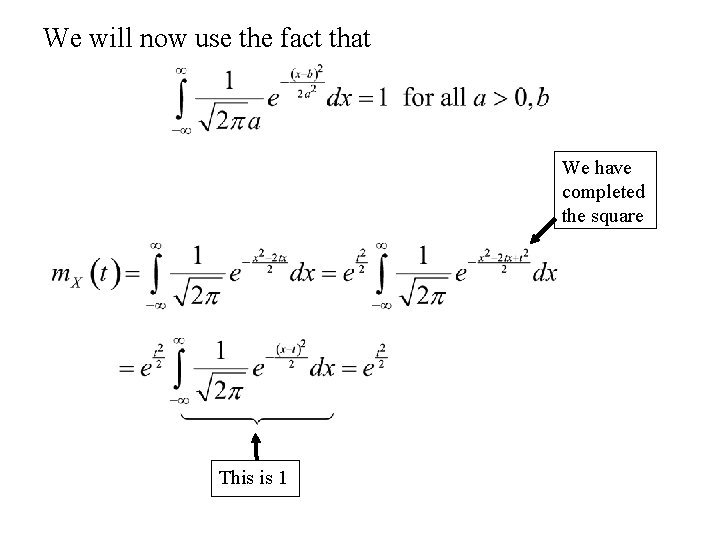
We will now use the fact that We have completed the square This is 1

4. The Gamma distribution (parameters a, l) The moment generating function of X , m. X(t) is:

We use the fact Equal to 1

Properties of Moment Generating Functions

1. m. X(0) = 1 Note: the moment generating functions of the following distributions satisfy the property m. X(0) = 1

We use the expansion of the exponential function:

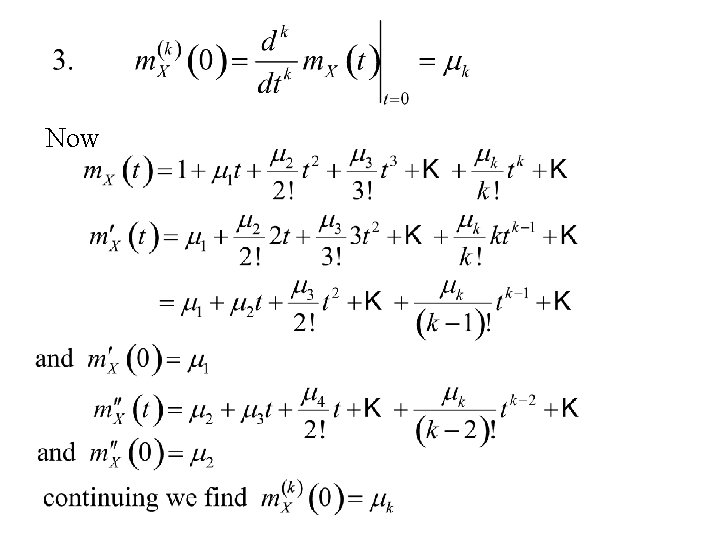
Now

Property 3 is very useful in determining the moments of a random variable X. Examples

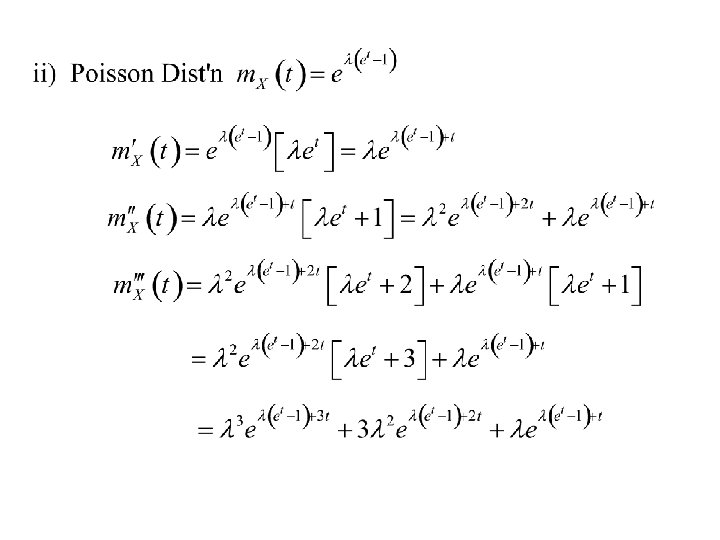
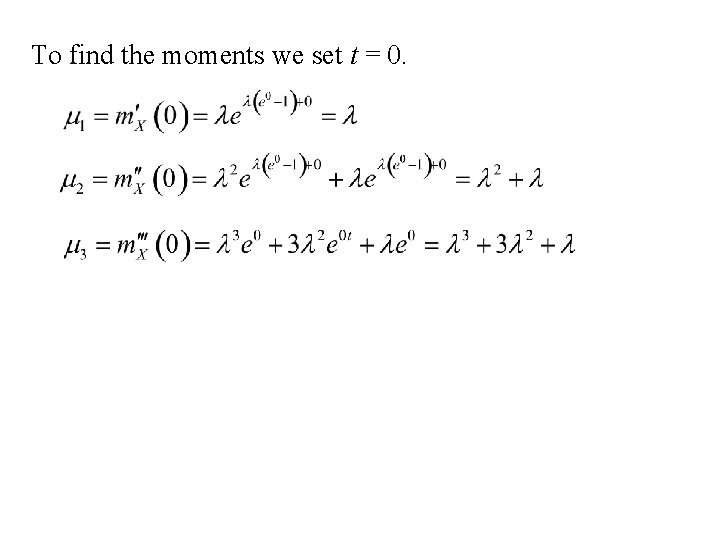
To find the moments we set t = 0.

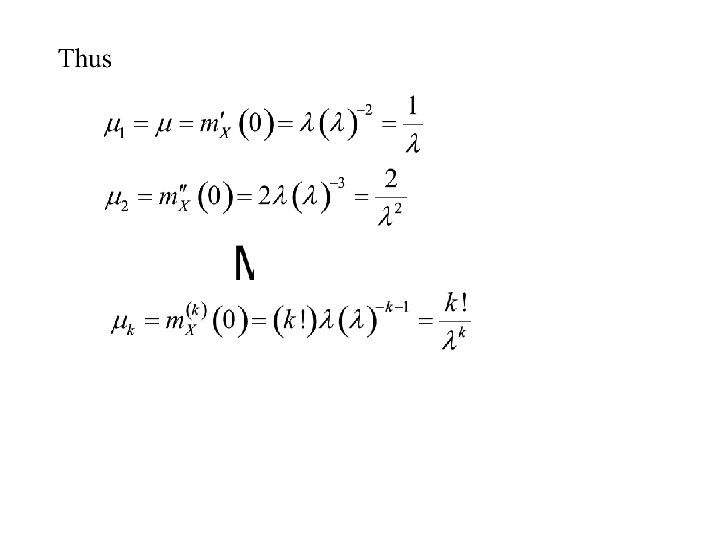
The moments for the exponential distribution can be calculated in an alternative way. This is note by expanding m. X(t) in powers of t and equating the coefficients of tk to the coefficients in: Equating the coefficients of tk we get:

The moments for the standard normal distribution We use the expansion of eu. We now equate the coefficients tk in:

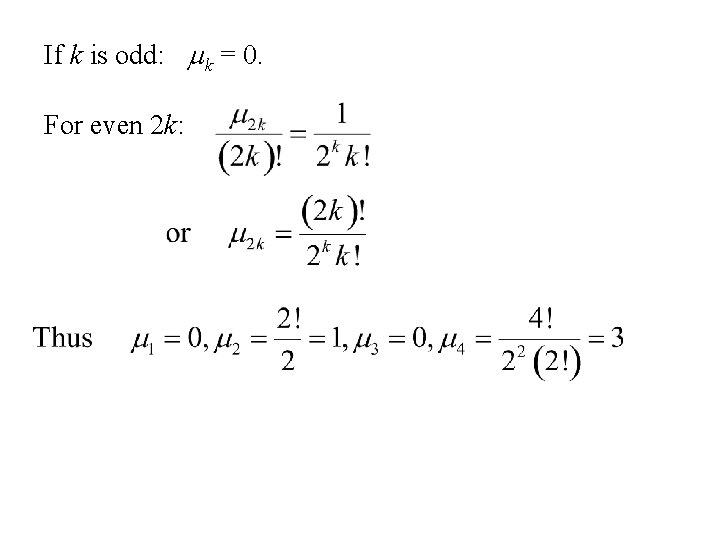
If k is odd: mk = 0. For even 2 k:

Summary Moments Moment generating functions

Moments of Random Variables The moment generating function

Examples 1. The Binomial distribution (parameters p, n) 2. The Poisson distribution (parameter l)

3. The Exponential distribution (parameter l) 4. The Standard Normal distribution (m = 0, s = 1)

5. The Gamma distribution (parameters a, l) 6. The Chi-square distribution (degrees of freedom n) (a = n/2, l = 1/2)

Properties of Moment Generating Functions 1. m. X(0) = 1

The log of Moment Generating Functions Let l. X (t) = ln m. X(t) = the log of the moment generating function

Thus l. X (t) = ln m. X(t) is very useful for calculating the mean and variance of a random variable

Examples 1. The Binomial distribution (parameters p, n)

2. The Poisson distribution (parameter l)

3. The Exponential distribution (parameter l)

4. The Standard Normal distribution (m = 0, s = 1)

5. The Gamma distribution (parameters a, l)

6. The Chi-square distribution (degrees of freedom n)

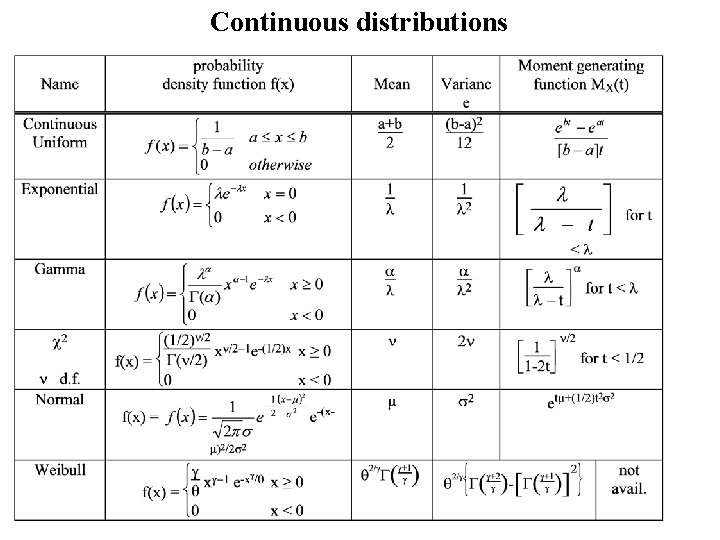
Continuous distributions