Molecular Symmetry Revision Symmetry operation motion of molecule

























- Slides: 37

Molecular Symmetry Revision Symmetry operation motion of molecule which leaves it indistinguishable from before. Symmetry element plane, line (axis) or point (centre) about which symmetry operation is performed. Point group quantitative measure of amount of symmetry possessed by a molecule.

Types of Symmetry Operation/Element (symbol) Operation (symbol) Axis of rotation (Cn) Rotation by m ´ (360/n)° (Cnm) Plane of symmetry (s) Reflection in plane (s) Centre of symmetry (i) Inversion at centre (i) Rotation/reflection axis (Sn) Rotation by m ´ (360/n)° followed by m ´ reflection in perpendicular plane (Snm) Identity (do nothing) (E) (None) Note – main axis drawn vertical by convention. Plane containing main axis = sv (vertical plane). Plane perpendicular to main axis = sh (horizontal plane). Sometimes two different types of vertical plane differentiated as sv and sd (dihedral plane) – examples and explanation later. If no rotation axis symbol is simply s.

Assignment of Molecules to Point Groups Step 1 Look for Cn axis – if found go to Step 2. Otherwise look for (i) plane of symmetry ® Cs (ii) centre of inversion ® Ci (iii) only identity ® C 1 Step 2 Look for n. C 2 ^ to Cn – if found go to Step 3. Otherwise look for. (i) sh ® Cnh (ii) n ´ sv ® Cnv (iii) no s ® Cn Step 3 Look for (i) (iii) sh n ´ sv no s ® Dnh ® Dnd ® Dn 'Special' Groups (i) Linear molecules – with no centre of symmetry C¥v - with centre of symmetry D¥h (ii) Tetrahedral molecules: Td (iii) Octahedral molecules: Oh

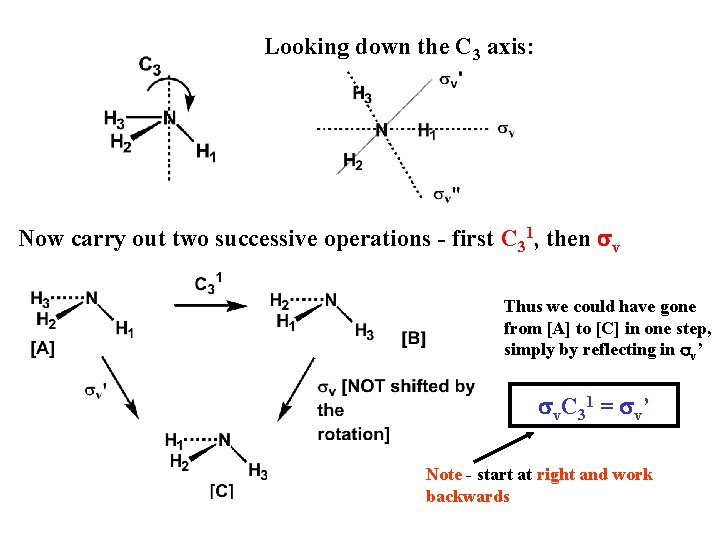
Effects of carrying out successive symmetry operations Definition: MULTIPLICATION of symmetry operations = sequential operation Simple examples of multiplication of symmetry operations: C 41 ´ C 41 = C 42 = C 21 ´ C 21 = C 22 = s ´ s = i ´ i = E What if we want to multiply together (i. e. perform successively) different symmetry operations? Take as an example the ammonia molecule, NH 3:

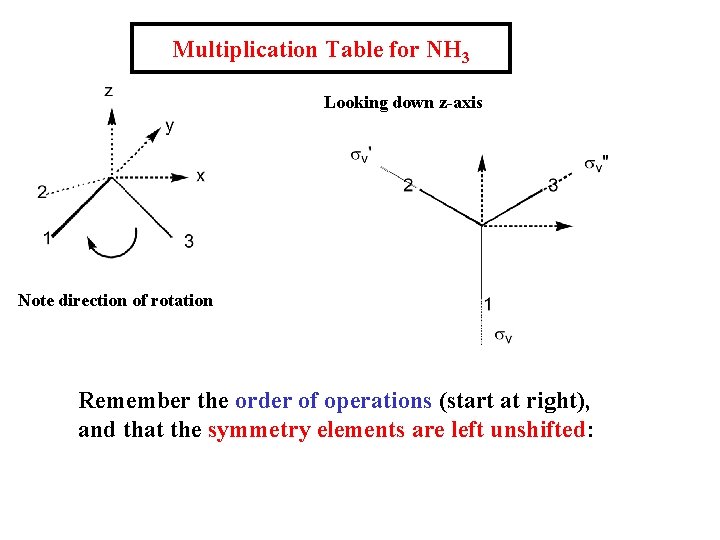
Looking down the C 3 axis: Now carry out two successive operations - first C 31, then sv Thus we could have gone from [A] to [C] in one step, simply by reflecting in sv’ sv. C 31 = sv’ Note - start at right and work backwards

The final result of carrying out successively (multiplying) two or more symmetry operations is always equivalent to a single symmetry operation characteristic of the molecule

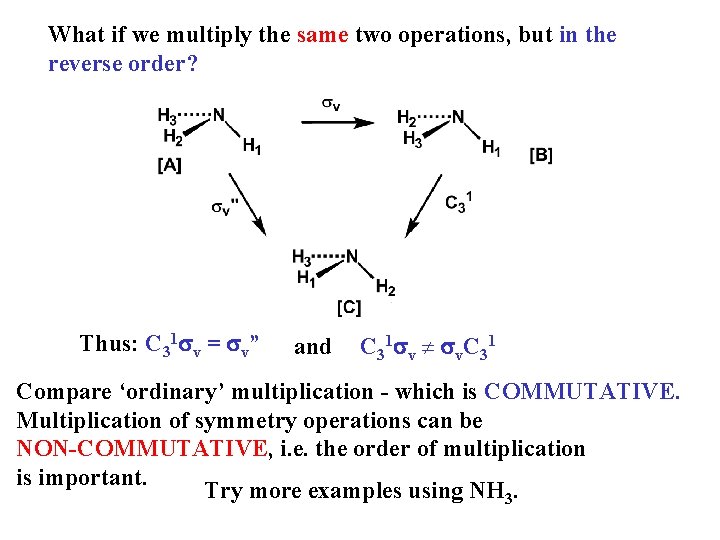
What if we multiply the same two operations, but in the reverse order? Thus: C 31 sv = sv” and C 31 sv ¹ sv. C 31 Compare ‘ordinary’ multiplication - which is COMMUTATIVE. Multiplication of symmetry operations can be NON-COMMUTATIVE, i. e. the order of multiplication is important. Try more examples using NH 3.

INVERSE OPERATIONS If any object has a symmetry operation A, then it must have another one, B, such that: AB = BA = E i. e. carrying out second exactly undoes the effects of the first. B is said to be the INVERSE of A, and is given the symbol A-1. Therefore: A A-1 = A-1 A = E For reflections and inversions, simply repeating the operation returns everything to its original place, i. e. s 2 = E and i 2 = E Thus a reflection or inversion is its own inverse, and s = s-1 and i = i-1

Not so simple for rotations. How do we get back to the original position? For C 31 (rotation by 120 o) we can get back by a further rotation by 240 o (C 32) C 32 C 31 = E = C 31 C 32 In general: and: Cnn-1 Cn 1 = E = Cn 1 Cnn-m Cnm = E = Cnm Cnn-m We can therefore say that Cnn-1 = Cn-1 etc.

For improper rotations (rotation/reflections) the position is similar, but Snn = E only when n is even, while Sn 2 n = E when n is odd. Therefore Snn-1 Sn 1 = E = Sn 1 Snn-1 when n is even Sn 2 n-1 Sn 1 = E = Sn 1 Sn 2 n-1 when n is odd Final (trivial) example: EE = E, therefore E = E-1 Hence - all symmetry operations possess inverses Why is this important?

We are going to use the symmetry properties of molecules to solve problems in spectroscopy, bonding theory etc. This will use a branch of maths called GROUP THEORY We need to show that collections of symmetry operations do constitute mathematical groups

BASIC PROPERTIES OF A GROUP Any collection of objects (A, B, C, D, …. ) is a group if it obeys the following four rules: (1) (2) (3) (4) One element combines with all of the others and leaves them unchanged. This is the IDENTITY (E) for which AE = EA = A for all members of the group. Every element must possess an INVERSE (X), such that AX = XA = E. We have just seen that this is true for symmetry operations. Any combination of two or more elements in the collection must be equivalent to a single element which is also a member of the collection, AB = C. Shown earlier to be true for symmetry operations. Although multiplication need not be COMMUTATIVE, it must be ASSOCIATIVE, i. e. A(BC) = (AB)C. This can also be proved to be true for symmetry operations. We have seen that multiplication of symmetry operations is often non-commutative.

Therefore, for any molecule, its collection of symmetry operations constitutes a GROUP

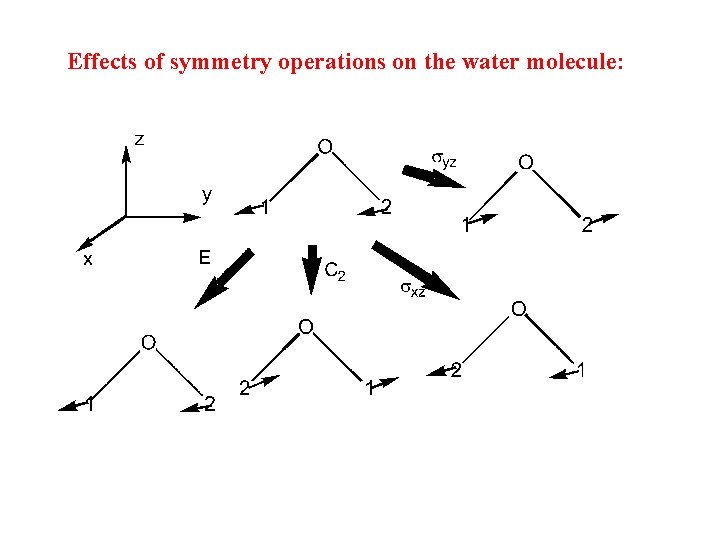
Effects of symmetry operations on the water molecule:

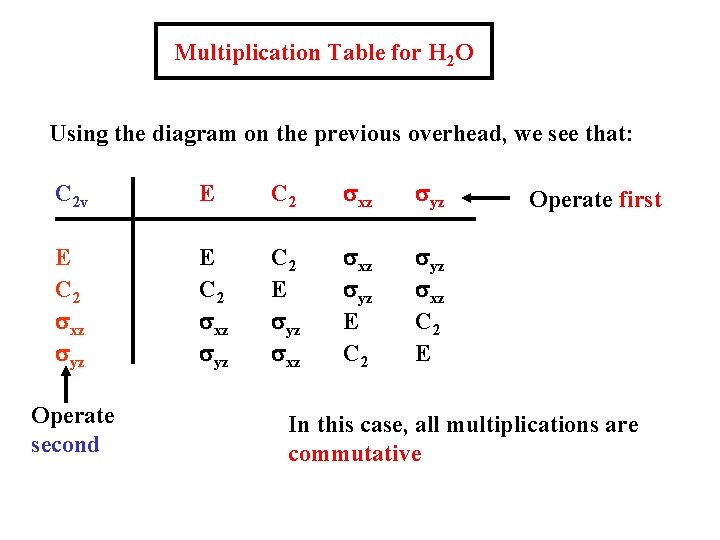
Multiplication Table for H 2 O Using the diagram on the previous overhead, we see that: C 2 v E C 2 sxz syz C 2 E syz sxz syz E C 2 syz sxz C 2 E Operate second Operate first In this case, all multiplications are commutative

Multiplication Table for NH 3 Looking down z-axis Note direction of rotation Remember the order of operations (start at right), and that the symmetry elements are left unshifted:

C 3 v E C 31 C 32 sv s v' s v” E C 31 C 32 sv s v' s v" E C 31 C 32 sv C 31 C 32 E sv' C 32 E C 31 sv" sv s v" s v' E s v' sv s v" C 31 s v" s v' sv C 32 etc. The completion of this table is left to you - see Tutorial Problem sheet. Note that the multiplications are often non-commutative - as seen earlier.

Classes of symmetry operations Use the C 3 v multiplication table. Carry out multiplication C 32 sv. C 31 - remember that C 32 is the INVERSE of C 31, so that this could be written as C 3 -1 sv. C 31. Use multiplication table to show that C 32 sv. C 31 = C 32 sv’ = sv” Now carry out similar multiplications X-1 sv. X (where X = any symmetry operation of C 3 v).

We find that the answer is always sv, sv’ or sv”. This is also true if the ‘central’ operation is sv’ or sv” The answer is never E, C 31 or C 32. To summarise these results: in the point group C 3 v, the operations sv, sv’ and sv” are in the same CLASS. Similarly X-1 EX = E for all X in group, and X-1 C 31 X or X-1 C 32 X = C 31 or C 32 for all X in group. Hence, in the point group C 3 v, the 6 symmetry operations can be grouped into 3 classes: E C 31, C 32 sv, sv’ , sv” The importance of this will be revealed later!

Representations of Groups Drawing diagrams to show effects of symmetry operations on molecules is too cumbersome. Need numerical representation of these effects. One way to obtain such representations is by attaching one or more VECTORS to the molecule. The effects of symmetry operations on these can be expressed numerically.

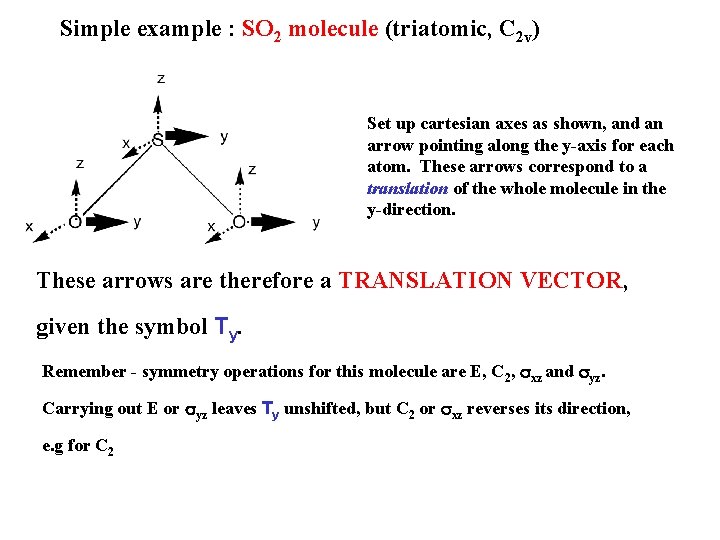
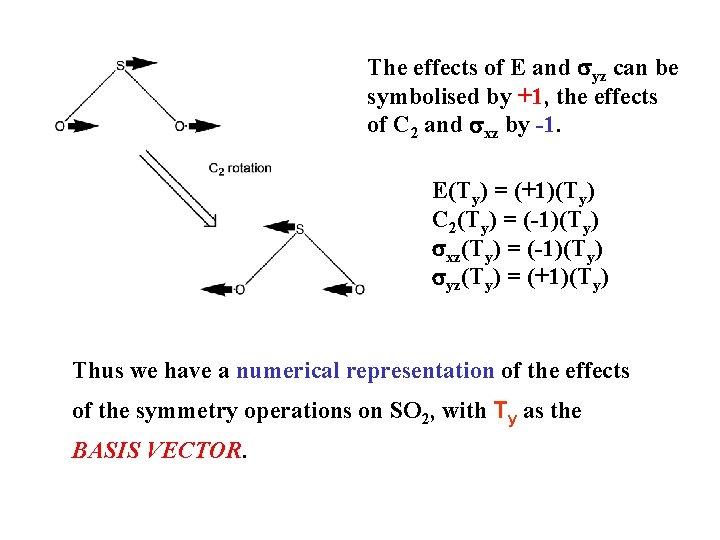
Simple example : SO 2 molecule (triatomic, C 2 v) Set up cartesian axes as shown, and an arrow pointing along the y-axis for each atom. These arrows correspond to a translation of the whole molecule in the y-direction. These arrows are therefore a TRANSLATION VECTOR, given the symbol Ty. Remember - symmetry operations for this molecule are E, C 2, sxz and syz. Carrying out E or syz leaves Ty unshifted, but C 2 or sxz reverses its direction, e. g for C 2

The effects of E and syz can be symbolised by +1, the effects of C 2 and sxz by -1. E(Ty) = (+1)(Ty) C 2(Ty) = (-1)(Ty) sxz(Ty) = (-1)(Ty) syz(Ty) = (+1)(Ty) Thus we have a numerical representation of the effects of the symmetry operations on SO 2, with Ty as the BASIS VECTOR.

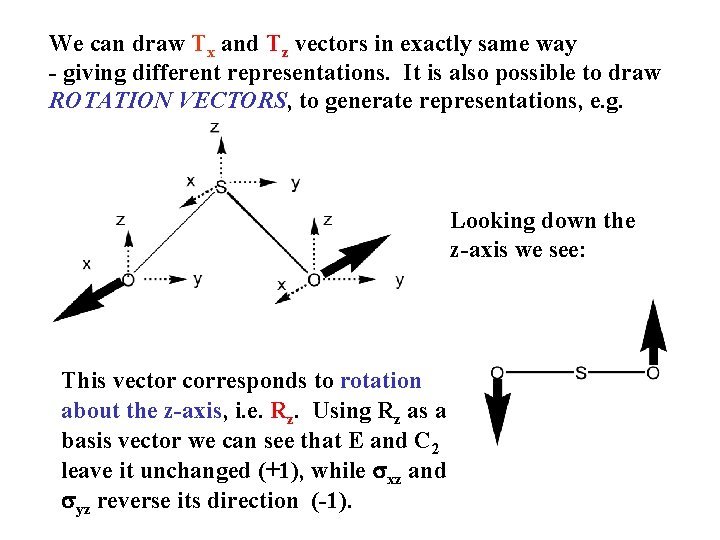
We can draw Tx and Tz vectors in exactly same way - giving different representations. It is also possible to draw ROTATION VECTORS, to generate representations, e. g. Looking down the z-axis we see: This vector corresponds to rotation about the z-axis, i. e. Rz. Using Rz as a basis vector we can see that E and C 2 leave it unchanged (+1), while sxz and syz reverse its direction (-1).

Similar vectors for rotation about the x and y axes (Rx and Ry) can be drawn, and we can summarise the representations produced by the 6 translation and rotation vectors : C 2 v E C 2 sxz syz +1 +1 +1 -1 -1 +1 -1 -1 +1 Tz Rz Tx, Ry Ty, Rx How can we prove that each of these is a true (faithful) representation of the group? The requirement for this is that the multiplication properties of the components of the representation should mirror exactly the operations that they are said to represent.

The representation must reproduce the multiplication table From C 2 v multiplication table we know that sxz syz = C 2 Consider the corresponding relationships in our representations of C 2 v: Tz representation : (+1) = (+1) Rz representation : (-1) = (+1) Tx/Ry representation : (+1)(-1) = (-1) Ty/Rx representation : (-1)(+1) = (-1) In each case, the numbers representing the two reflections multiply to give the number representing C 2 - just like the operations themselves.

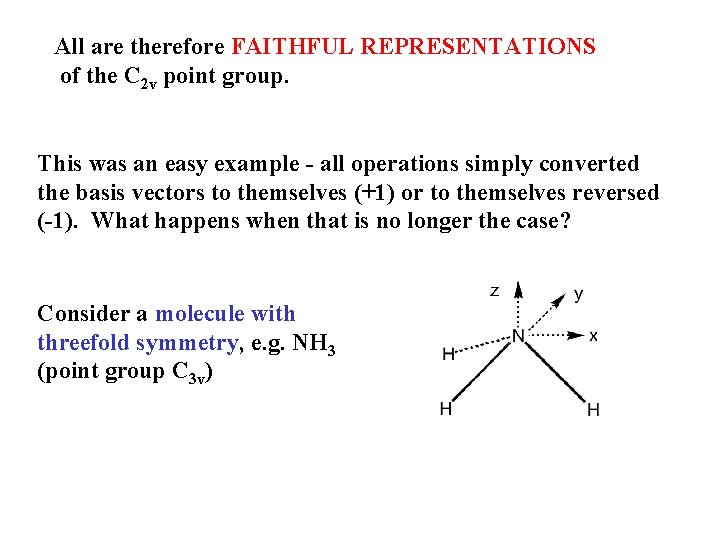
All are therefore FAITHFUL REPRESENTATIONS of the C 2 v point group. This was an easy example - all operations simply converted the basis vectors to themselves (+1) or to themselves reversed (-1). What happens when that is no longer the case? Consider a molecule with threefold symmetry, e. g. NH 3 (point group C 3 v)

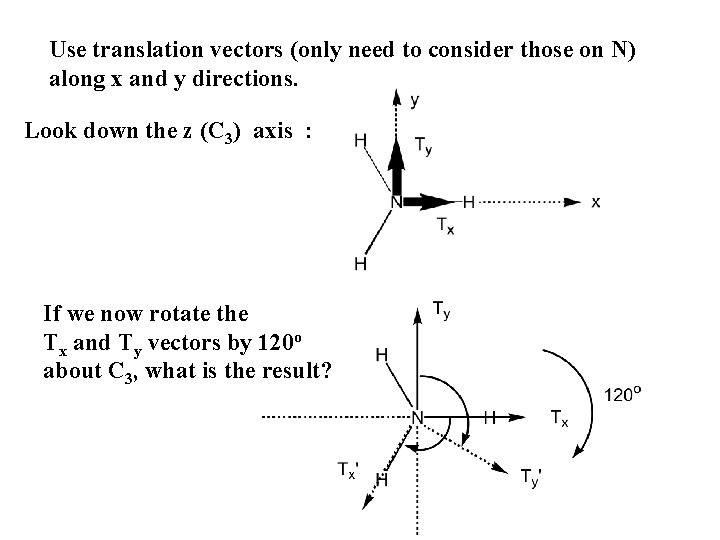
Use translation vectors (only need to consider those on N) along x and y directions. Look down the z (C 3) axis : If we now rotate the Tx and Ty vectors by 120 o about C 3, what is the result?

What is the relationship between the "new" vectors, Tx' and Ty'. and the "old" vectors, Tx and Ty? This can be expressed by a simple trigonometric relationship (i. e. determine the components of new vectors along directions of old). Components of "new" vectors in directions of 'old' vectors : Tx' = (cos 120 o)Tx - (sin 120 o)Ty Ty' = (sin 120 o)Tx + (cos 120 o)Ty Inserting the numerical values: Tx' = -(1/2)Tx - (Ö 3/2)Ty Ty' = +(Ö 3/2)Tx - (1/2)Ty Because symmetry operations of C 3 v mix Tx and Ty together, they cannot be separated.

These equations can be written more conveniently in terms of MATRICES : We now need a digression to explain what matrices are, and how we can multiply them together.

MATRICES For more details - see "Group Theory for Chemists" Chapter 3. Matrices are arrays of numbers (rectangular or square). Their multiplication properties are as follows: XY = Z When the matrices are written out in full we have the arrangement shown on the next slide.

ROW where: COLUMN Notes: 1. No. of columns in X = No. of rows in Y 2. If X is n x p, and Y is p x m, then Z is n x m 3. Summarise process as multiplying ith row of X by kth column of Y to give zik.

For each symmetry operation of C 3 v, we can write out an equivalent matrix equation. Each time there is a 2 x 2 TRANSFORMATION MATRIX which transforms Tx and Ty into a new pair of They are as follows: vectors.

It is also possible to draw out rotation vectors Rx and Ry, and it can be shown that they transform in exactly the same way as do Tx and Ty (i. e. same set of transformation vectors). N. B. Not easy to visualise Rx and Ry!

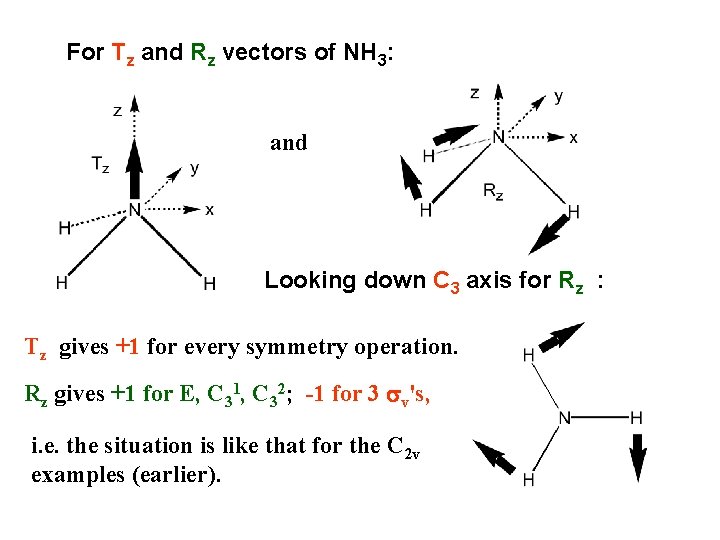
For Tz and Rz vectors of NH 3: and Looking down C 3 axis for Rz : Tz gives +1 for every symmetry operation. Rz gives +1 for E, C 31, C 32; -1 for 3 sv's, i. e. the situation is like that for the C 2 v examples (earlier).

We can summarise the transformation matrices for all of the T and R vectors for NH 3 Note that 1 vector gives 1 x 1 matrix, i. e. a number, 2 vectors give 2 x 2 matrices.

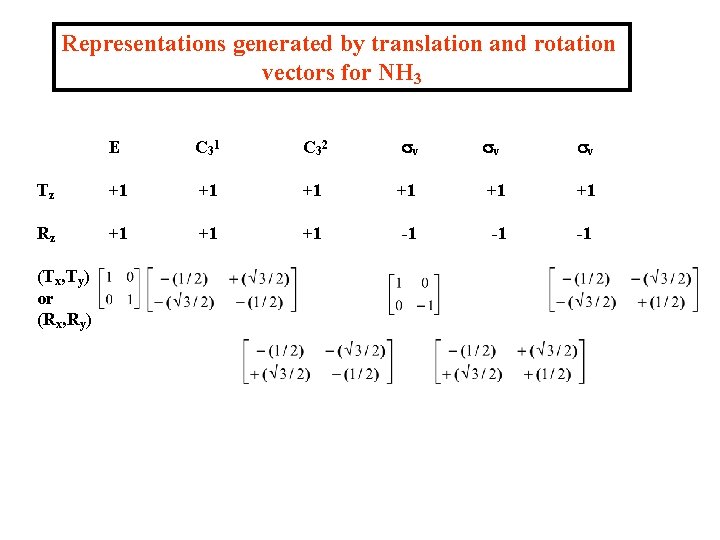
Representations generated by translation and rotation vectors for NH 3 E C 3 1 C 3 2 sv sv sv Tz +1 +1 +1 Rz +1 +1 +1 -1 -1 -1 (Tx, Ty) or (Rx, Ry)

In each case the set of 1 x 1 (=numbers) or 2 x 2 transformation matrices is a REPRESENTATION of C 3 v - easy to show for Tz and Rz; for others we can show that the matrices multiply in the same way as the operations themselves. Thus - can use translation or rotation vectors for any molecules to generate representations. BASIS VECTORS ® REPRESENTATIONS
 Passive sentence
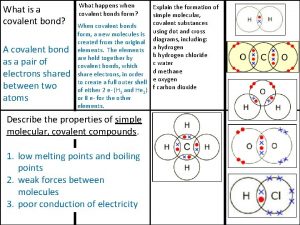
Passive sentence Covalent bond melting point
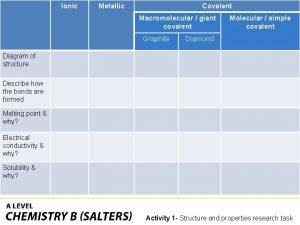
Covalent bond melting point Ionic covalent metallic
Ionic covalent metallic Giant molecular structure vs simple molecular structure
Giant molecular structure vs simple molecular structure Range of motion types
Range of motion types What is the formula of simple harmonic motion
What is the formula of simple harmonic motion An object in motion stays in motion
An object in motion stays in motion Chapter 2 section 1 describing motion answer key
Chapter 2 section 1 describing motion answer key Measuring motion
Measuring motion Section 1 describing motion worksheet answer key
Section 1 describing motion worksheet answer key Chapter 1 lesson 2 describing motion answer key
Chapter 1 lesson 2 describing motion answer key Motion section 1 describing motion
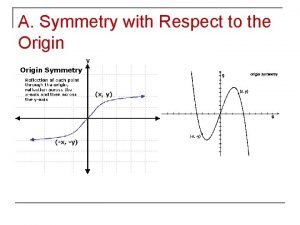
Motion section 1 describing motion Respect to origin
Respect to origin Symmetry in nature ppt
Symmetry in nature ppt Enzymes are composed of what organic molecule
Enzymes are composed of what organic molecule Are water molecules polar
Are water molecules polar Moles formual
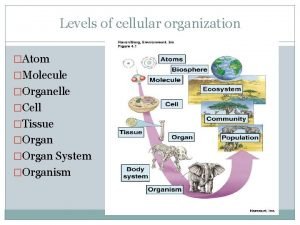
Moles formual Molecule organelle cell
Molecule organelle cell Nucleotide structure labeled
Nucleotide structure labeled Molecular shapes polar or nonpolar
Molecular shapes polar or nonpolar Organelle organization
Organelle organization What is atomicity
What is atomicity Water molecule evaporation
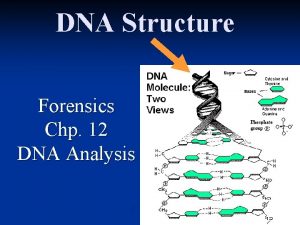
Water molecule evaporation Dna molecule two views
Dna molecule two views Ikatan hidrogen
Ikatan hidrogen Phosphodiester bond
Phosphodiester bond What is the difference between molecule and compound
What is the difference between molecule and compound Compound vs molecule
Compound vs molecule A chemists shorthand way of representing chemical reaction.
A chemists shorthand way of representing chemical reaction. Describe the polar characteristics of a water molecule.
Describe the polar characteristics of a water molecule. Compound vs molecule
Compound vs molecule Formula?
Formula? Ligand signaling molecule
Ligand signaling molecule Flour molecule
Flour molecule Where are neurotransmitters produced
Where are neurotransmitters produced Carbohydrate organic compound
Carbohydrate organic compound Cell tissue
Cell tissue What are the weakest attractions between molecules
What are the weakest attractions between molecules