Molecular orbitals for polyatomic systems The Hckel approximation

Molecular orbitals for polyatomic systems The Hückel approximation Here, we investigate conjugated molecules in which there is an alternation of single and double bonds along a chain of carbon atoms. In the Hückel approach, the orbitals are treated separately from the orbitals, the latter form a rigid framework that determine the general shape of the molecule. All C are considered similar only one type of coulomb integral for the C 2 p atomic orbitals involved in the molecular orbitals spread over the molecule. A. The secular determinant The molecular orbitals are expressed as linear combinations of C 2 pz atomic orbitals (LCAO), which are perpendicular to the molecular plane. Ethene, CH 2=CH 2: =c. AA + c. BB, where A and B are the C 2 pz orbitals of each carbon atoms. Butadiene, CH 2=CH-CH=CH 2: =c. AA + c. BB+cc. C + c. DD The coefficients can be optimized by the same procedure described before: express the total energy E as a function of the ci and then minimize the E with respect to those coefficients ci. Inject the energy solutions in the secular equations and extract the coefficients minimizing E.

Energy in the LCAO approach (1) Numerator: 1 is a Coulomb integral: it is related to the energy of the e- when it occupies atome 1. ( < 0) is a Resonance integral: it is zero if the orbital don’t overlap. (at Re, <0) (1) Denominator: (1) is the overlap integral related to the overlap of the 2 AO

Let’s find the “zeros” or roots of the polynomial vs. c. A and c. B We want the c. A minimizing E, we then impose: We want the c. B minimizing E, we then impose: Secular equations In order to have a solution, other than the simple solution c. A= c. B= 0, we must have: Secular determinant should be zero The 2 roots give the energies of the bonding and antibonding molecular orbitals formed from the AOs

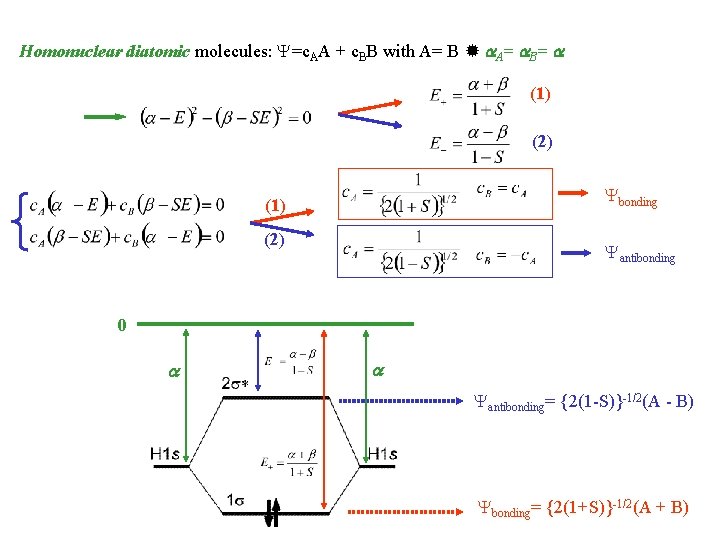
Homonuclear diatomic molecules: =c. AA + c. BB with A= B= (1) (2) bonding (1) (2) antibonding 0 antibonding= {2(1 -S)}-1/2(A - B) bonding= {2(1+S)}-1/2(A + B)

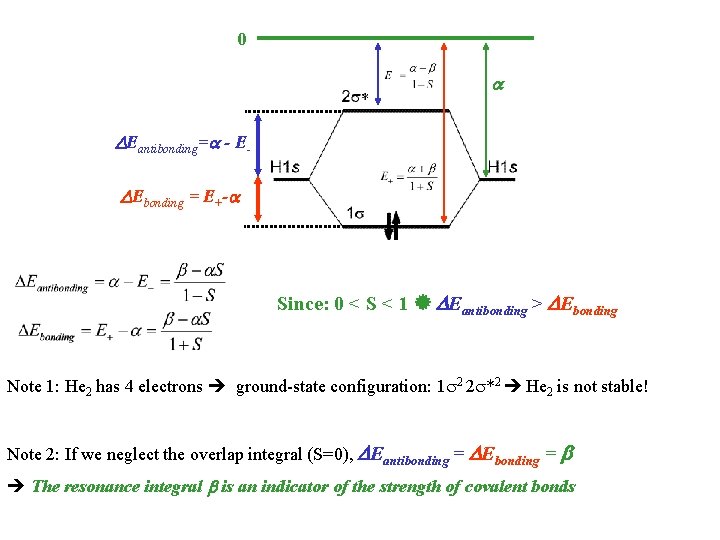
0 Eantibonding= - E Ebonding = E+- Since: 0 < S < 1 Eantibonding > Ebonding Note 1: He 2 has 4 electrons ground-state configuration: 1 2 2 *2 He 2 is not stable! Note 2: If we neglect the overlap integral (S=0), Eantibonding = Ebonding = The resonance integral is an indicator of the strength of covalent bonds

Following these methods and since A= B= , we obtain those secular determinants: Ethene, CH 2=CH 2: Butadiene, CH 2=CH-CH=CH 2: i i+2 Hückel approximation: 1) All overlap integrals Sij= 0 (i 2 pz i+1 j). 2) All resonance integrals between non-neighbors, i, i+n=0 with n 2 3) All resonance integrals between neighbors are equal, i, i+1= i+1, i+2 = Severe approximation, but it allows us to calculate the general picture of the molecular orbital energy levels.

B. Ethene and frontier orbitals Within the Hückel approximation, the secular determinant becomes: E- = - energy of the Lowest Unoccupied Molecular Orbital (LUMO) E+ = + energy of the Highest Occupied Molecular Orbital (HOMO) LUMO= 2 * 2| | HOMO= 1 HOMO and LUMO are the frontier orbitals of a molecule. those are important orbitals because they are largely responsible for many chemical and optical properties of the molecule. Note: The energy needed to excite electronically the molecule, from the ground state 1 2 to the first excited state 1 1 2 *1 is provided roughly by 2| | ( is often around -0. 8 e. V) Chap 17

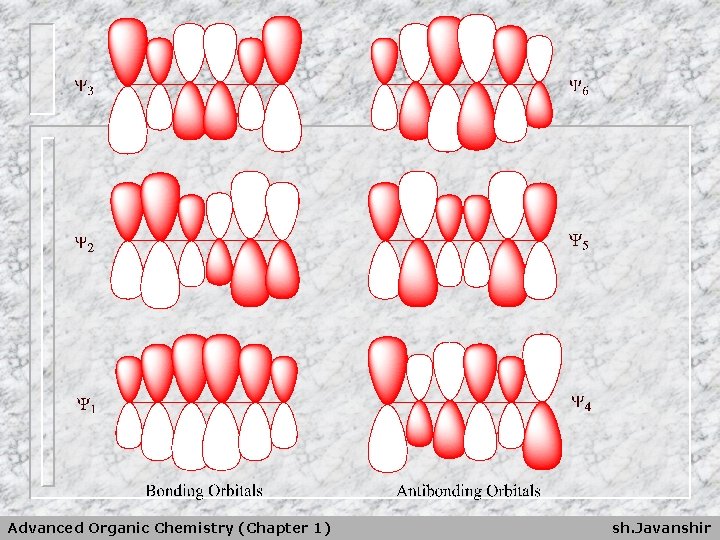
Butadiene and delocalization energy 4 th order polynomial 4 roots E There is 1 e- in each 2 pz orbital of the four carbon atoms 4 electrons to accommodate in the 4 -type molecular orbitals the ground state configuration is 1 2 2 2 3 nodes = E 4 The greater the number of internuclear nodes, the = E 3 LUMO= 3 * Butadiene C 4 H 6: total -electron binding energy, E is E = 2 E 1+2 E 2= 4 + 4. 48 with two -bonds 2 nodes = E 2 1 node HOMO= 1 0 node = E 1 Top view of the MOs higher the energy of the orbital Ethene C 2 H 4: E = 2 + 2 with one -bond Two ethene molecules give: E = 4 + 4 for two separated -bonds. The energy of the butadiene molecule with two bonds lies lower by 0. 48 (-36 k. J/mol) than the sum of two individual -bonds: this extra-stabilization of a conjugated system is called the “delocalization energy”

Energy Levels for Linear Polyenes : Coulomb Integral : Resonance Integral n: Number of Carbons j: Specified Carbon Number Advanced Organic Chemistry (Chapter 1) sh. Javanshir

n Orbital coefficients: are given by : ﺿﺮﺍیﺐ ﺍﺗﻤی - n - total number of atoms in the conjugated chain r - atom number ( i. e. 1, 2, …. , n ) j - quantum number, identifying the MO ( = 1, 2, …. , n ) Advanced Organic Chemistry (Chapter 1) sh. Javanshir

E = + m j n ﺗﺮﺍﺯﻫﺎی ﺍﻧﺮژی Note that the cosine function varies only between the limiting values of – 1 and +1. = ﺗﻌﺪﺍﺩ ﺍﺗﻢ ﻫﺎی کﺮﺑﻦ ﺣﻠﻘﻪ n Advanced Organic Chemistry (Chapter 1) sh. Javanshir

Energy Levels for 1, 3, 5 -Hexatriene Advanced Organic Chemistry (Chapter 1) sh. Javanshir

Delocalization Energy (DE) for 1, 3, 5 -Hexatriene with Respect to Localized System 6 Electrons fill three 1, 2, and 3 orbitals and therefore: Advanced Organic Chemistry (Chapter 1) sh. Javanshir

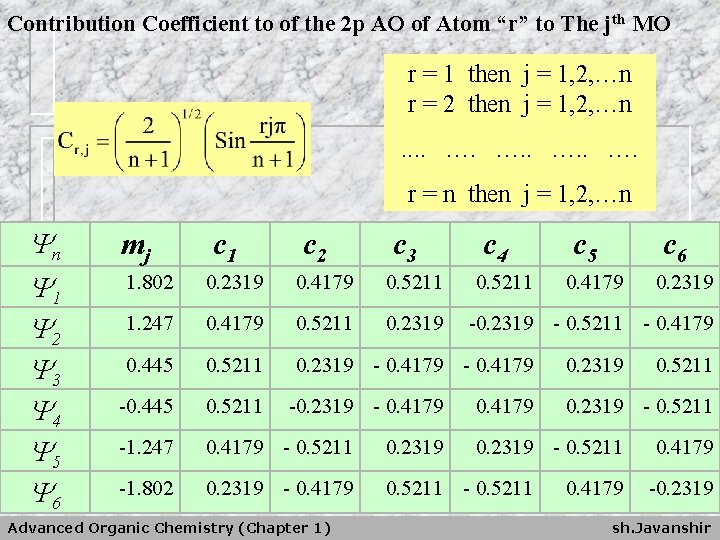
Contribution Coefficient to of the 2 p AO of Atom “r” to The jth MO r = 1 then j = 1, 2, …n r = 2 then j = 1, 2, …n. . …. …. r = n then j = 1, 2, …n Yn Y 1 Y 2 Y 3 Y 4 Y 5 Y 6 mj c 1 c 2 c 3 c 4 1. 802 0. 2319 0. 4179 0. 5211 1. 247 0. 4179 0. 5211 0. 2319 0. 445 0. 5211 0. 2319 - 0. 4179 -0. 445 0. 5211 -1. 247 0. 4179 - 0. 5211 0. 2319 -1. 802 0. 2319 - 0. 4179 0. 5211 -0. 2319 - 0. 4179 Advanced Organic Chemistry (Chapter 1) 0. 5211 c 5 c 6 0. 4179 0. 2319 - 0. 5211 - 0. 4179 0. 2319 0. 5211 0. 2319 - 0. 5211 0. 4179 -0. 2319 sh. Javanshir

Advanced Organic Chemistry (Chapter 1) sh. Javanshir

Energy Levels for Planar and Conjugated Cyclic Systems for n odd for n even Advanced Organic Chemistry (Chapter 1) sh. Javanshir

Frost Circles u Frost circle: a graphic method for determining the relative order of pi MOs in planar, fully conjugated monocyclic compounds • inscribe a polygon of the same number of sides as the ring to be examined such that one of the vertices is at the bottom of the ring • the relative energies of the MOs in the ring are given by where the vertices touch the circle u Those MOs • below the horizontal line through the center of the ring are bonding MOs • on the horizontal line are nonbonding MOs • above the horizontal line are antibonding MOs Advanced Organic Chemistry (Chapter 1) sh. Javanshir

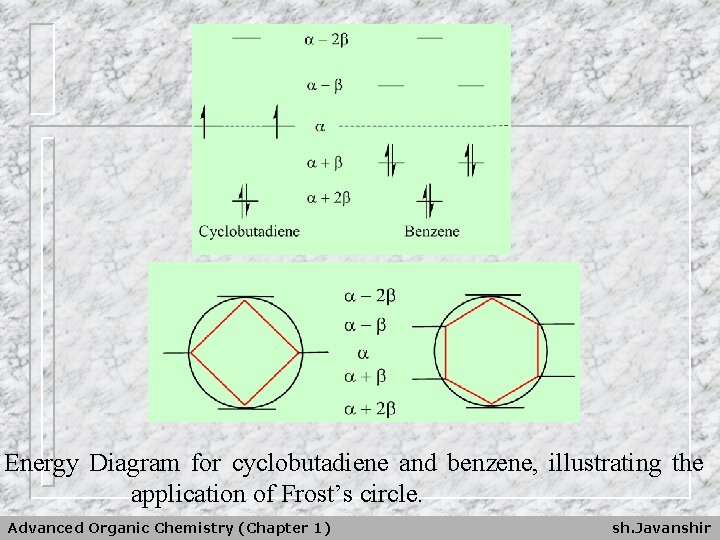
Energy Diagram for cyclobutadiene and benzene, illustrating the application of Frost’s circle. Advanced Organic Chemistry (Chapter 1) sh. Javanshir

1. Cyclobutadiene: a) Triplet Ground State b) Etotal = 4 +4 then DE = 0 2. Benzene: a) Singlet Ground State b) Etotal= 6 +8 then DE = 2 Advanced Organic Chemistry (Chapter 1) sh. Javanshir

Musulin-Frost diagrams: MO diagrams without the maths Graphical device for constructing MO energy diagrams: Frost & Musulin J. Chem. Phys. 1953, 21, 572 (DOI) & Zimmerman J. Am. Chem. Soc. 1966, 88, 1564 (DOI) HMO energy levels for cyclic polyene n = 3 to n = 8. Advanced Organic Chemistry (Chapter 1) sh. Javanshir

- - 0. 618 + 0. 618 + 2 Energy diagram for C 3 H 3 and C 5 H 5 systems. 1. C 3 H 3+ Cation: Etotal = 2 +4 then DE = 2 Etotal= 4 + 2 then DE = -2 3. C 5 H 5 Anion: Etotal = 6 +6. 472 then DE = 0. 472 4. C 5 H 5+ Cation: Etotal = 4 +5. 236 then DE = 1. 236 - 2. C 3 H 3 Anion: - Advanced Organic Chemistry (Chapter 1) sh. Javanshir

Applications of HMO calculations n delocalization energy (DE) total pi energy compared to that of a localized reference system n charge density for a given carbon atom, coefficient squared gives electron density in each MO Advanced Organic Chemistry (Chapter 1) sh. Javanshir