Molecular Orbitals Atomic orbitals interact to form molecular

Molecular Orbitals

Atomic orbitals interact to form molecular orbitals Electrons are placed in molecular orbitals following the same rules as for atomic orbitals In terms of approximate solutions to the Scrödinger equation Molecular Orbitals are linear combinations of atomic orbitals (LCAO) Y = caya + cbyb (for diatomic molecules) Interactions depend on the symmetry properties and the relative energies of the atomic orbitals

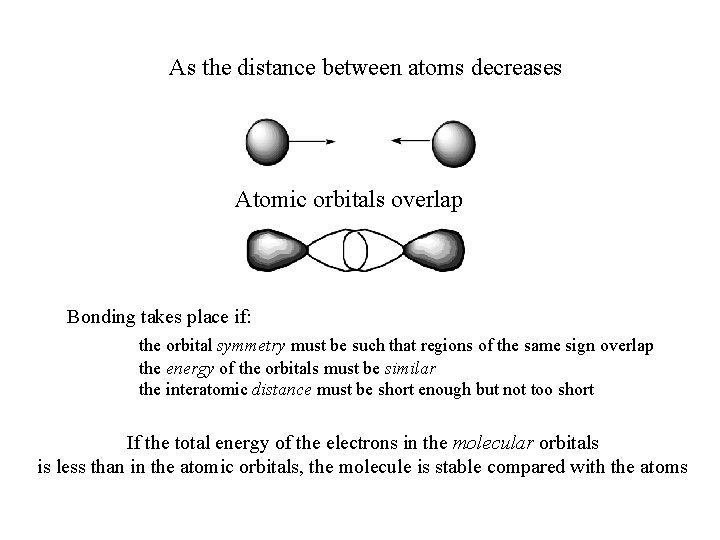
As the distance between atoms decreases Atomic orbitals overlap Bonding takes place if: the orbital symmetry must be such that regions of the same sign overlap the energy of the orbitals must be similar the interatomic distance must be short enough but not too short If the total energy of the electrons in the molecular orbitals is less than in the atomic orbitals, the molecule is stable compared with the atoms

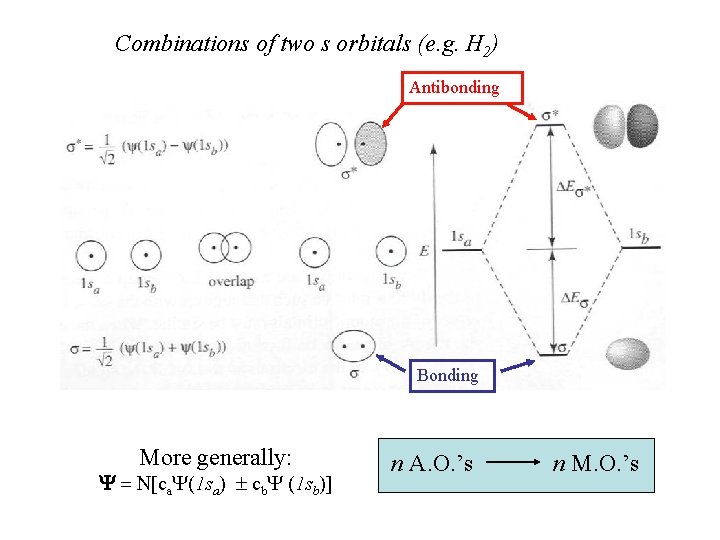
Combinations of two s orbitals (e. g. H 2) Antibonding Bonding More generally: Y = N[ca. Y(1 sa) ± cb. Y (1 sb)] n A. O. ’s n M. O. ’s

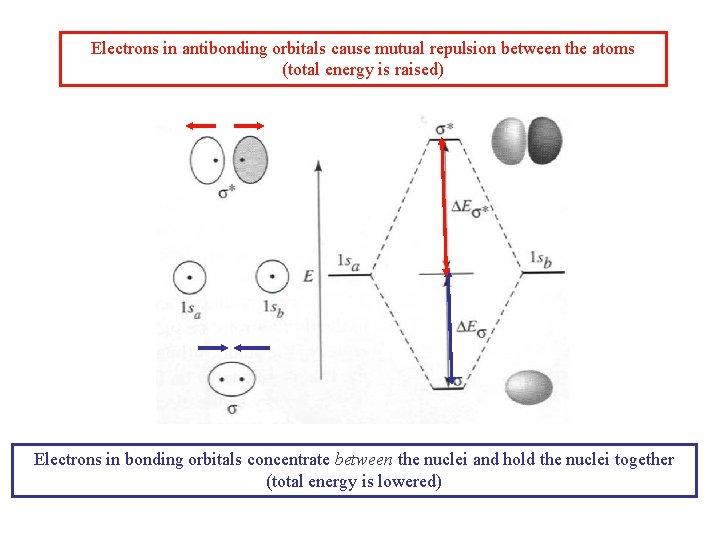
Electrons in antibonding orbitals cause mutual repulsion between the atoms (total energy is raised) Electrons in bonding orbitals concentrate between the nuclei and hold the nuclei together (total energy is lowered)

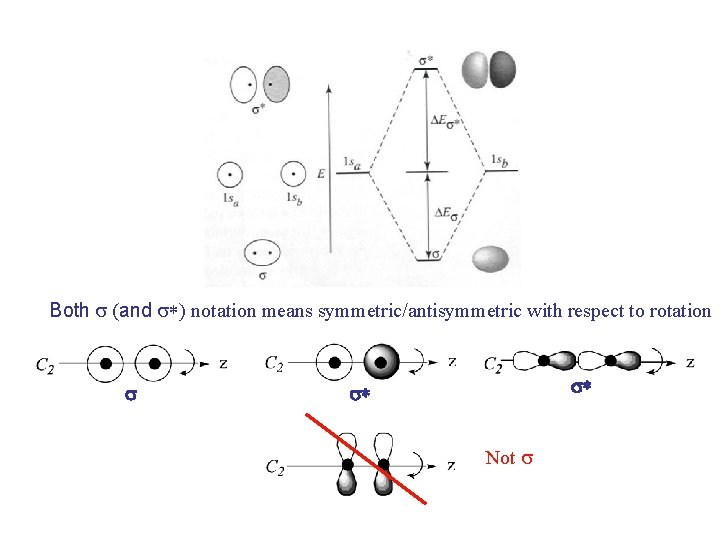
Both s (and s*) notation means symmetric/antisymmetric with respect to rotation s s* s* Not s

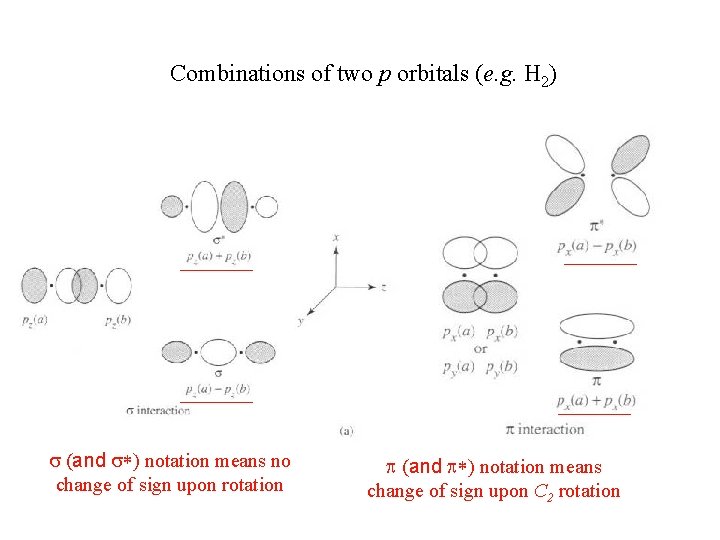
Combinations of two p orbitals (e. g. H 2) s (and s*) notation means no change of sign upon rotation p (and p*) notation means change of sign upon C 2 rotation

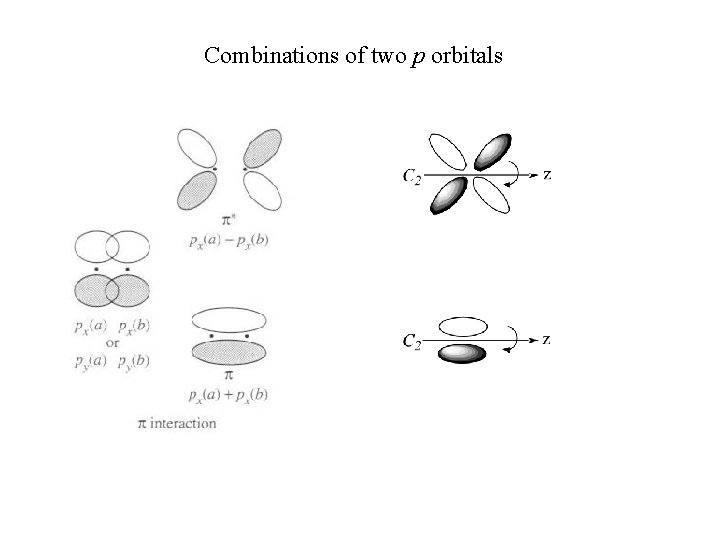
Combinations of two p orbitals

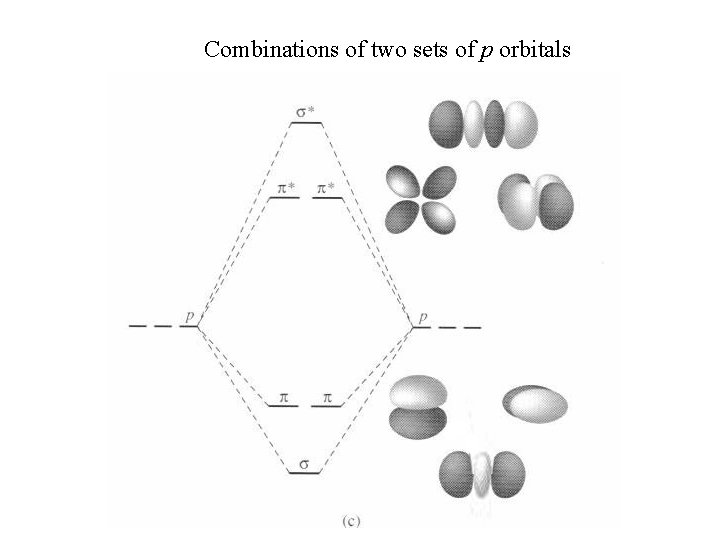
Combinations of two sets of p orbitals

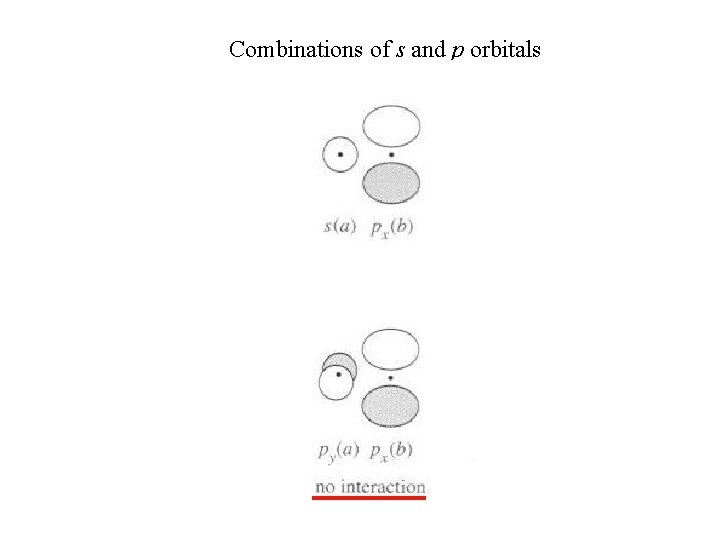
Combinations of s and p orbitals

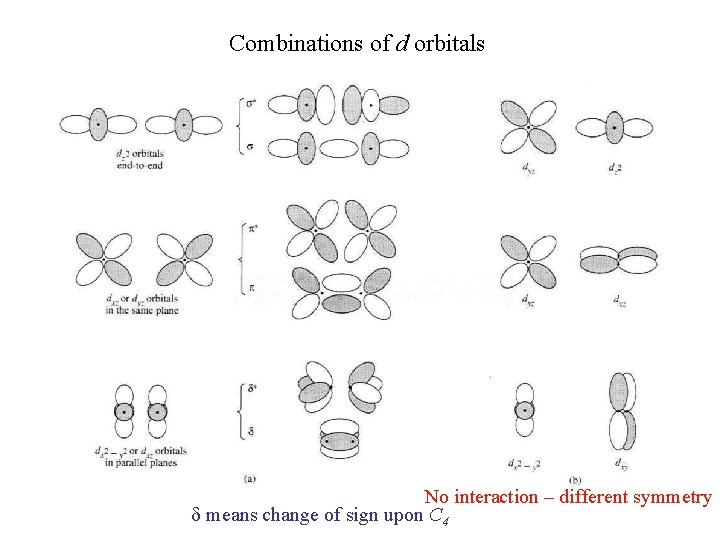
Combinations of d orbitals No interaction – different symmetry d means change of sign upon C 4

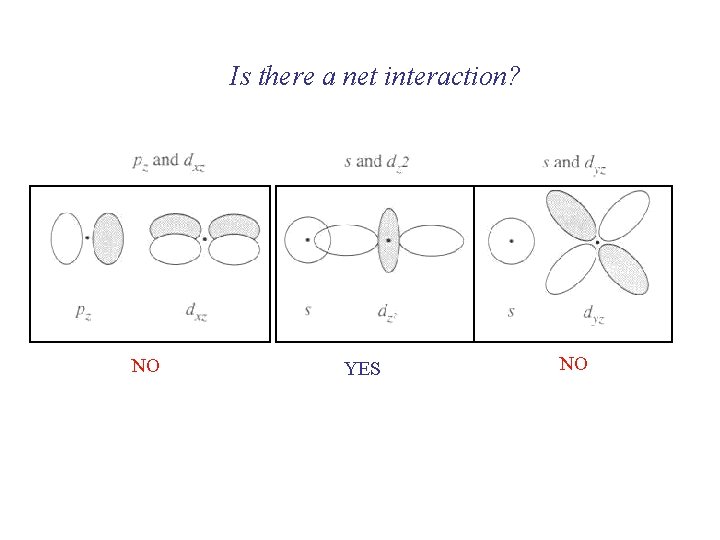
Is there a net interaction? NO YES NO

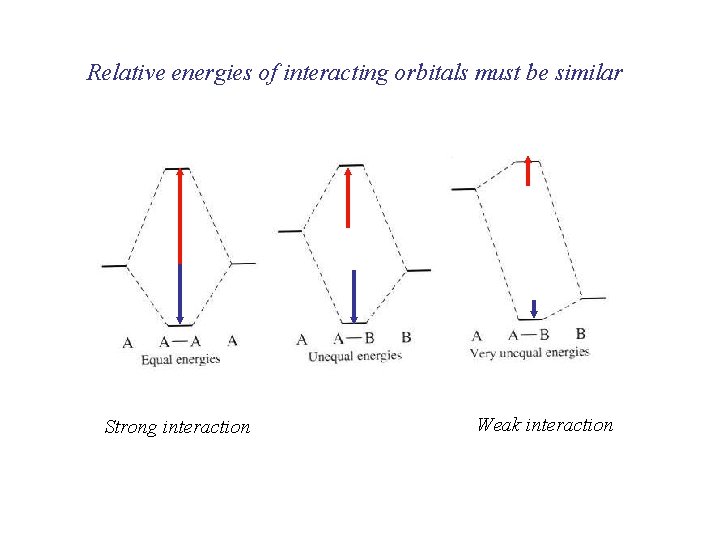
Relative energies of interacting orbitals must be similar Strong interaction Weak interaction

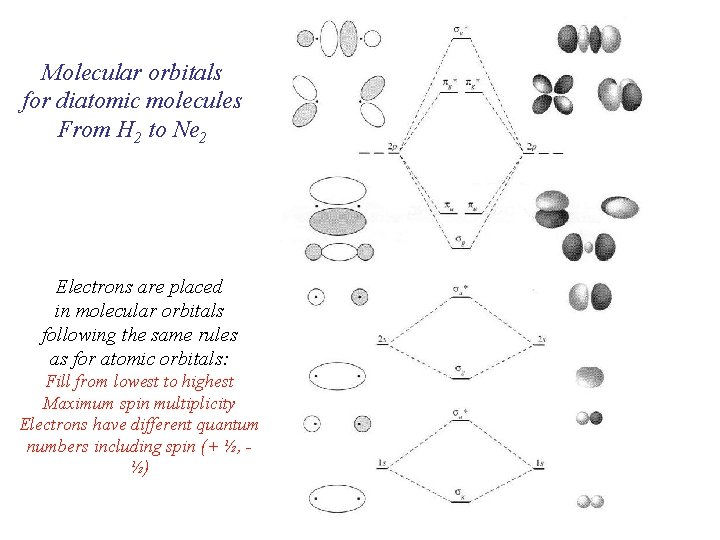
Molecular orbitals for diatomic molecules From H 2 to Ne 2 Electrons are placed in molecular orbitals following the same rules as for atomic orbitals: Fill from lowest to highest Maximum spin multiplicity Electrons have different quantum numbers including spin (+ ½, ½)

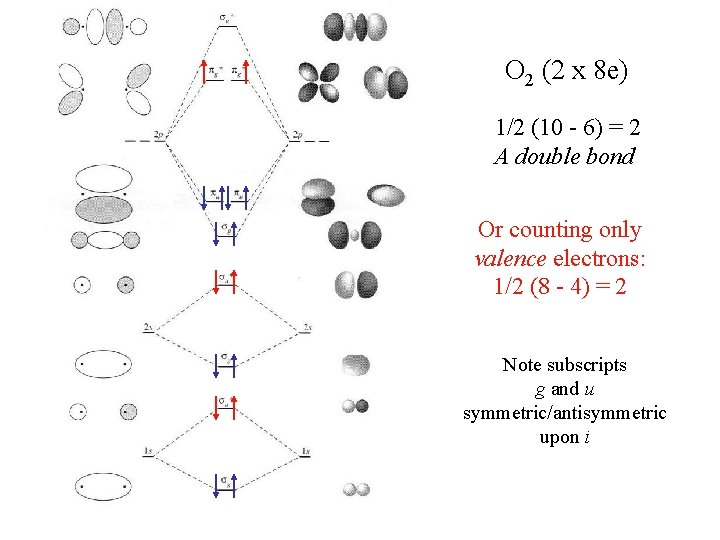
O 2 (2 x 8 e) 1/2 (10 - 6) = 2 A double bond Or counting only valence electrons: 1/2 (8 - 4) = 2 Note subscripts g and u symmetric/antisymmetric upon i

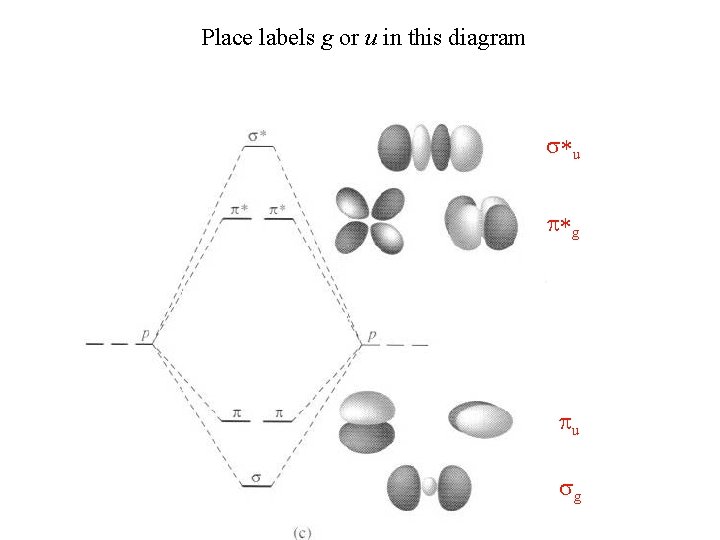
Place labels g or u in this diagram s*u p*g pu sg

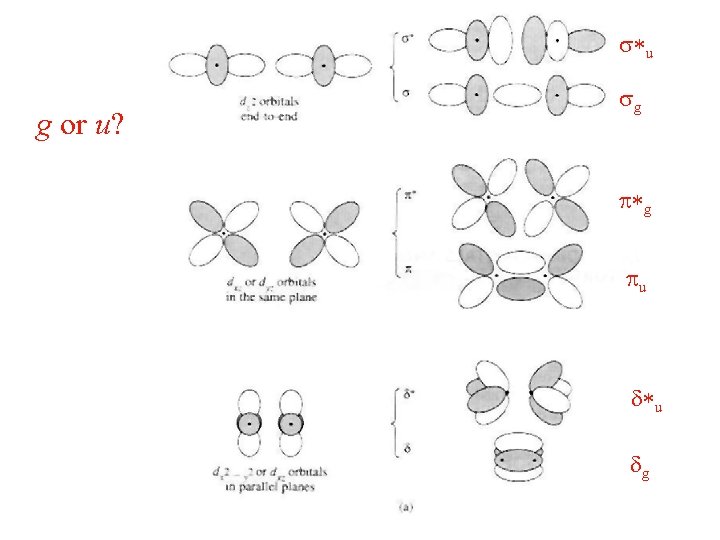
s*u g or u? sg p*g pu d*u dg

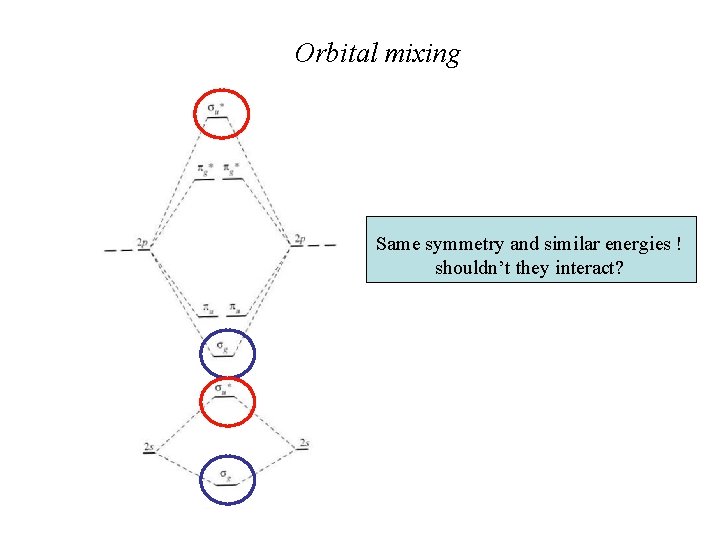
Orbital mixing Same symmetry and similar energies ! shouldn’t they interact?

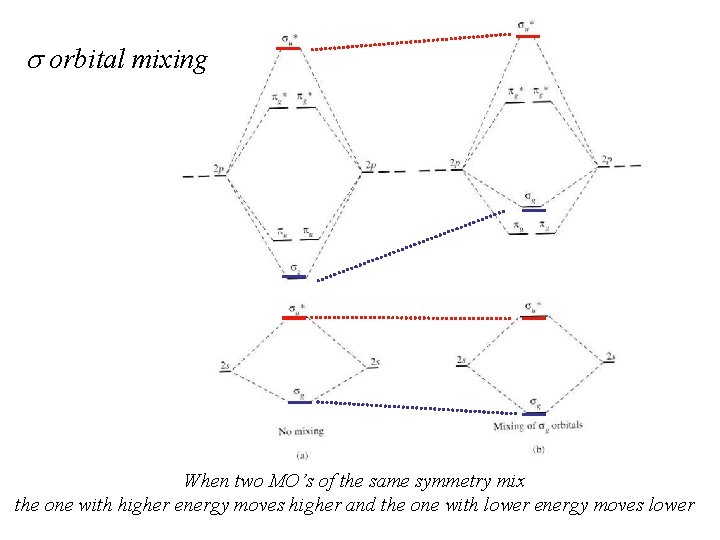
s orbital mixing When two MO’s of the same symmetry mix the one with higher energy moves higher and the one with lower energy moves lower

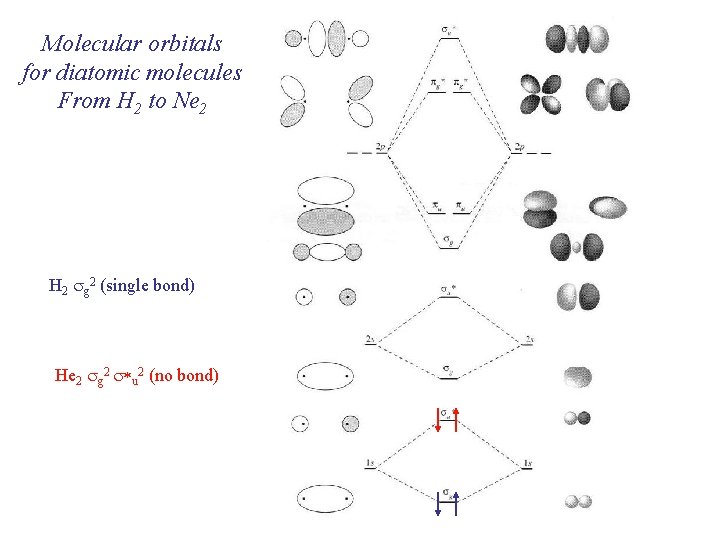
Molecular orbitals for diatomic molecules From H 2 to Ne 2 H 2 sg 2 (single bond) He 2 sg 2 s*u 2 (no bond)

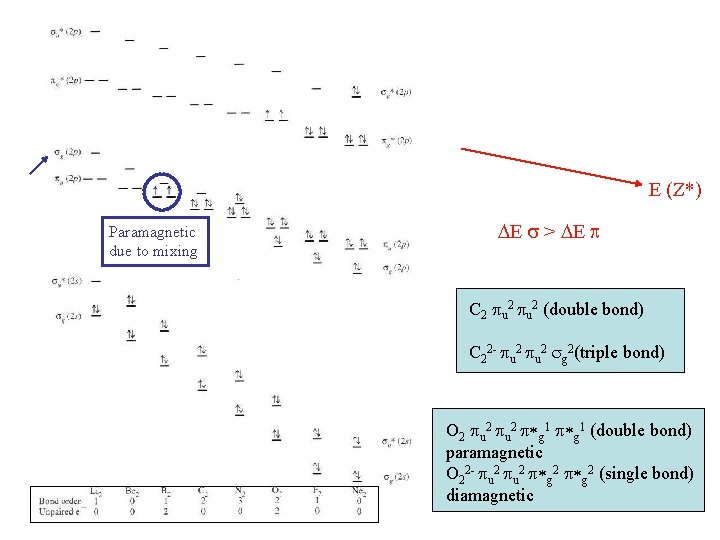
E (Z*) Paramagnetic due to mixing DE s > DE p C 2 pu 2 (double bond) C 22 - pu 2 sg 2(triple bond) O 2 pu 2 p*g 1 (double bond) paramagnetic O 22 - pu 2 p*g 2 (single bond) diamagnetic

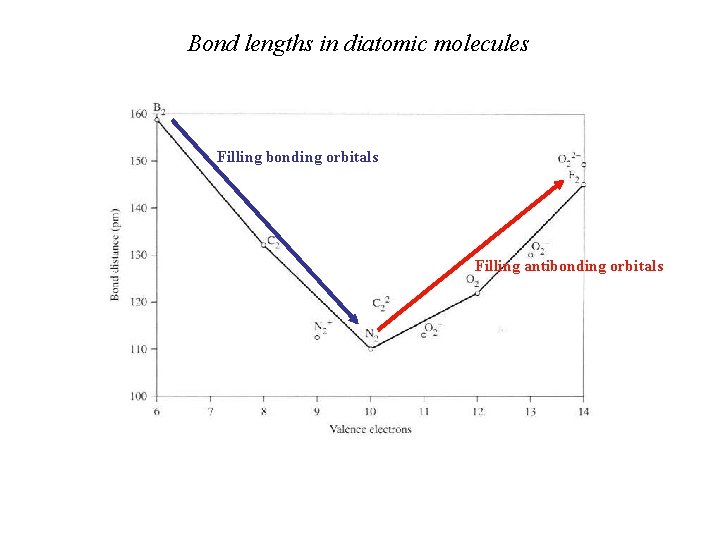
Bond lengths in diatomic molecules Filling bonding orbitals Filling antibonding orbitals

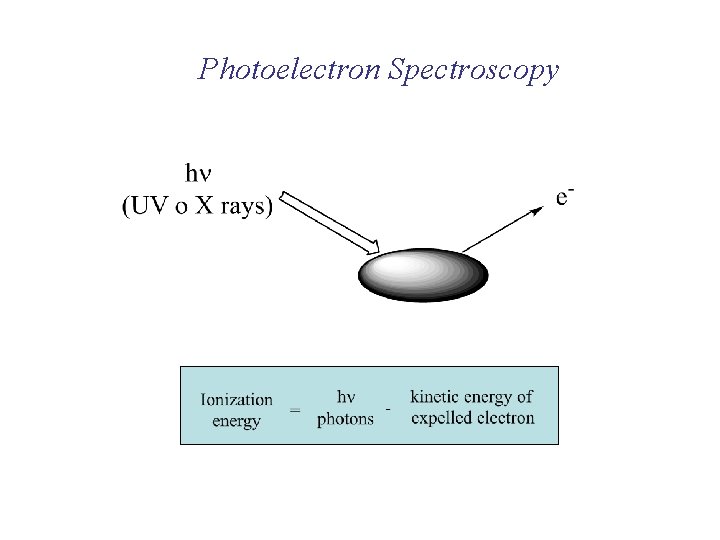
Photoelectron Spectroscopy

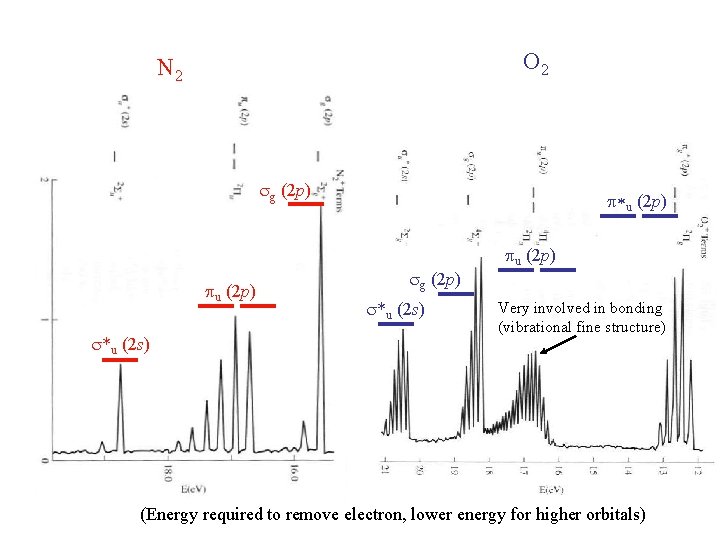
O 2 N 2 sg (2 p) pu (2 p) s*u (2 s) p*u (2 p) sg (2 p) s*u (2 s) pu (2 p) Very involved in bonding (vibrational fine structure) (Energy required to remove electron, lower energy for higher orbitals)

Simple Molecular Orbital Theory A molecular orbital, f, is expressed as a linear combination of atomic orbitals, holding two electrons. The multi-electron wavefunction and the multi-electron Hamiltonian are Where hi is the energy operator for electron i and involves only electron i

MO Theory - 2 Seek F such that Divide by F(1, 2, 3…) recognizing that hi works only on electron i. Since each term in the summation depends on the coordinates of a different electron then each term must equal a constant.

MO Theory - 3 Recall the expansion of a molecular orbital in terms of the atomic orbitals. Multiply by uk and integrate. Define These integrals are fixed numerical values. Substituting the expansion for f

MO Theory - 4 For k = 1 to AO These are the secular equations. The number of such equations is equal to the number of atomic orbitals, AO. There are AO equations with AO unknowns, the al. For there to be a nontrivial (all al equal to zero) solution to the set of secular equations then the determinant below must equal zero

MO Theory 6 Drastic assumptions can now be made. We will use the simple Huckle approximations. hi, i = a, if orbital i is on a carbon atom. Si, i = 1, normalized atomic orbitals hi, j = b, if atom i bonded to atom j, zero otherwise Expand the secular determinant into a polynomial of degree AO in e. Obtain the allowed values of e by finding the roots of the polynomial. Choose one particular value of e, substitute into the secular equations and obtain the coefficients of the atomic orbitals within the molecular orbital.

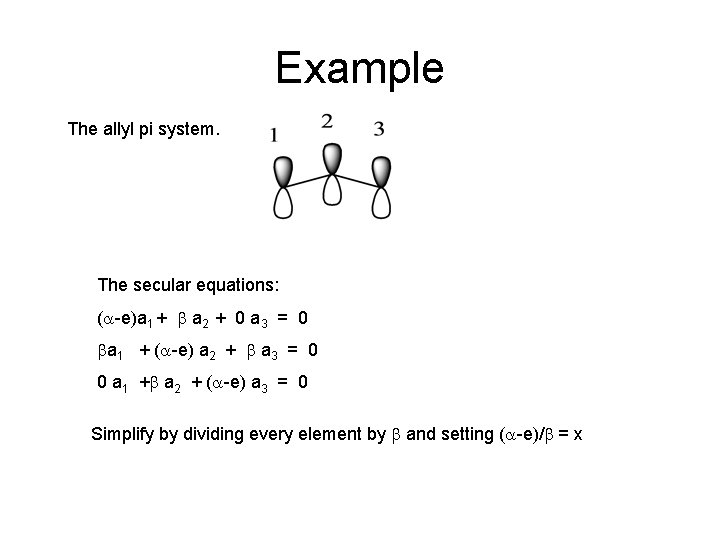
Example The allyl pi system. The secular equations: (a-e)a 1 + b a 2 + 0 a 3 = 0 ba 1 + (a-e) a 2 + b a 3 = 0 0 a 1 +b a 2 + (a-e) a 3 = 0 Simplify by dividing every element by b and setting (a-e)/b = x

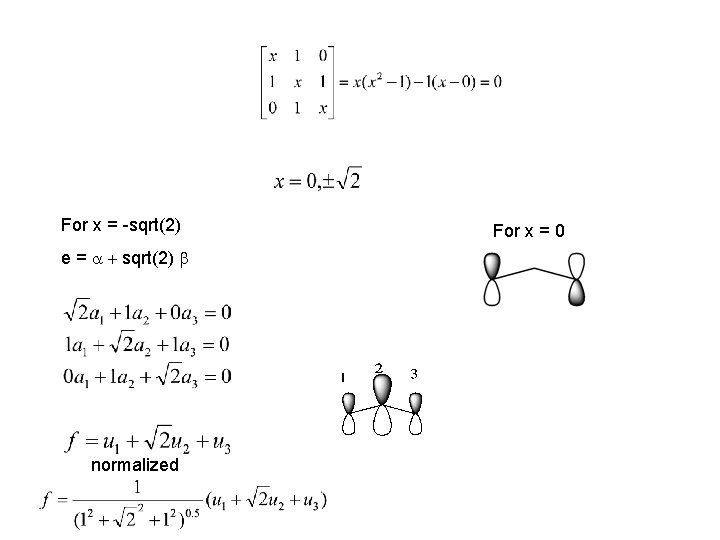
For x = -sqrt(2) e = a + sqrt(2) b normalized For x = 0

Verify that hf = ef

Perturbation Theory The Hamiltonian is divided into two parts: H 0 and H 1 H 0 is the Hamiltonian of for a known system for which we have the solutions: the energies, e 0, and the wavefunctions, f 0. H 0 f 0 = e 0 f 0 H 1 is a change to the system and the Hamiltonian which renders approximation desirable. The change to the energies and the wavefunctions are expressed as a summation.

Corrections Energy Zero order (no correction): ei 0 First Order correction: Wave functions corrections to f 0 i Zero order (no correction): f 0 i First order correction:

Example Pi system only: Perturbed system: allyl system Unperturbed system: ethylene + methyl radical

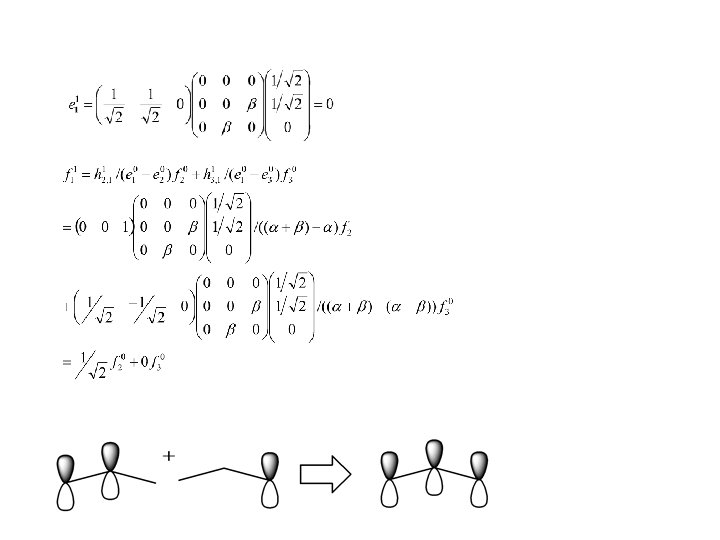
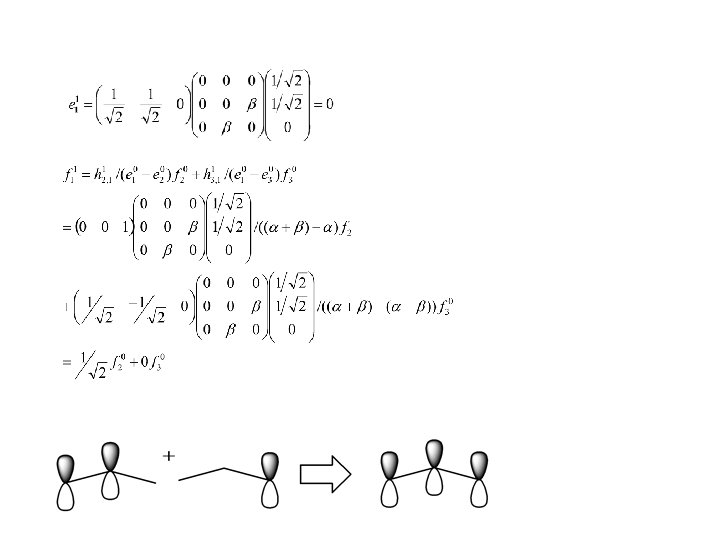
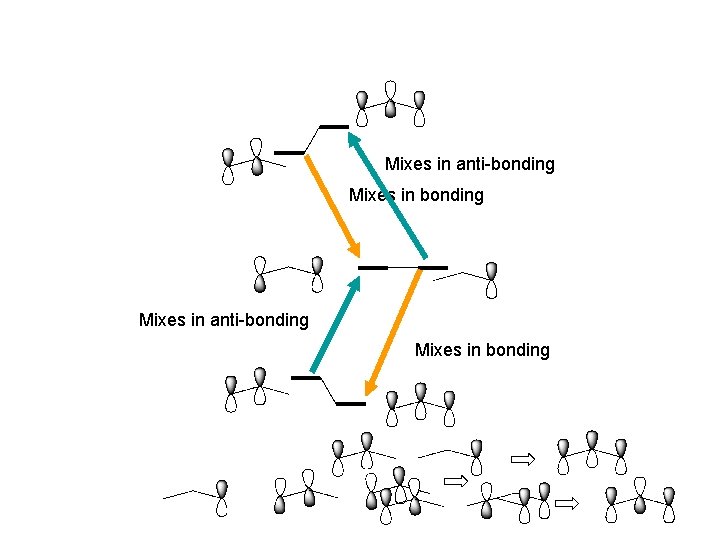
Mixes in anti-bonding Mixes in bonding

Projection Operator Algorithm of creating an object forming a basis for an irreducible rep from an arbitrary function. Where the projection operator results from using the symmetry operations multiplied by characters of the irreducible reps. j indicates the desired symmetry. lj is the dimension of the irreducible rep. Starting with the 1 s. A create a function of A 1 sym ¼(E 1 s. A + C 21 s. A + sv’ 1 s. A) = ½(1 s. A + 1 s. B)