Molecular Modeling The compendium of methods for mimicking

Molecular Modeling The compendium of methods for mimicking the behavior of molecules or molecular systems

Points for Consideration Remember • Molecular modeling forms a model of the real world • Thus we are studying the model, not the world • A model is valid as long as it reproduces the real world

Why Use Molecular Modeling? (and not deal directly with the real world? ) Fast, accurate and relatively cheap way to: • • • Study molecular properties Rationalize and interpret experimental results Make predictions for yet unstudied systems Study hypothetical systems Design new molecules And • Understand reactants probe ? products

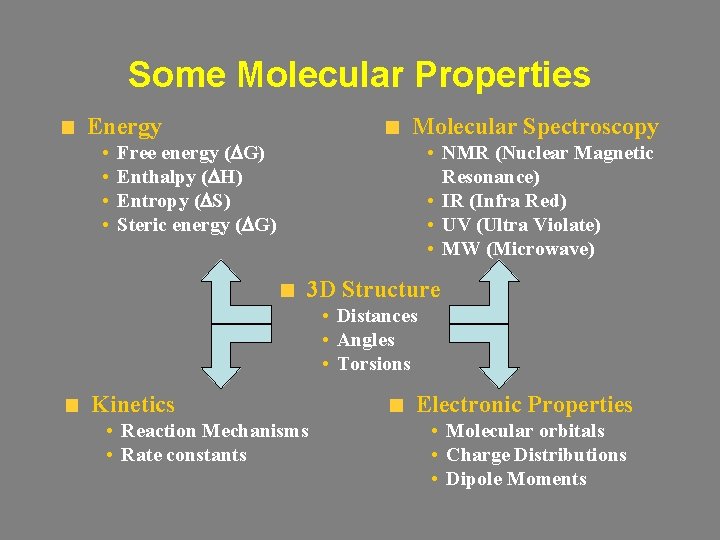
Some Molecular Properties Molecular Spectroscopy Energy • • • NMR (Nuclear Magnetic Resonance) • IR (Infra Red) • UV (Ultra Violate) • MW (Microwave) Free energy (DG) Enthalpy (DH) Entropy (DS) Steric energy (DG) 3 D Structure • Distances • Angles • Torsions Kinetics • Reaction Mechanisms • Rate constants Electronic Properties • Molecular orbitals • Charge Distributions • Dipole Moments

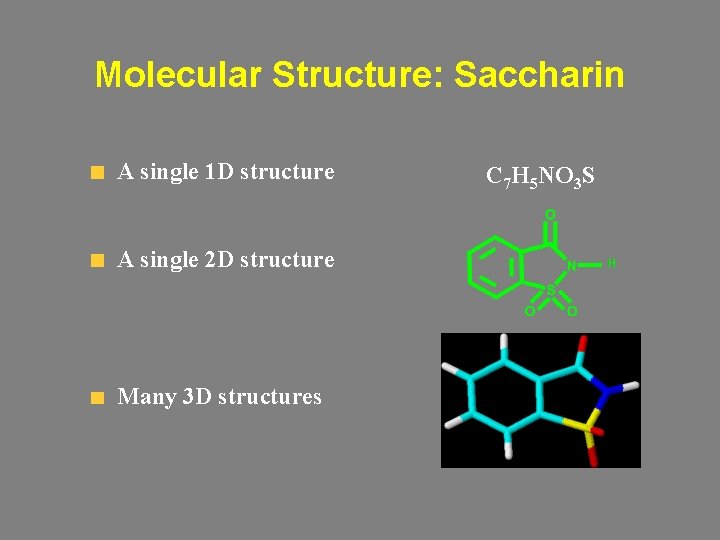
Molecular Structure: Saccharin A single 1 D structure A single 2 D structure Many 3 D structures C 7 H 5 NO 3 S

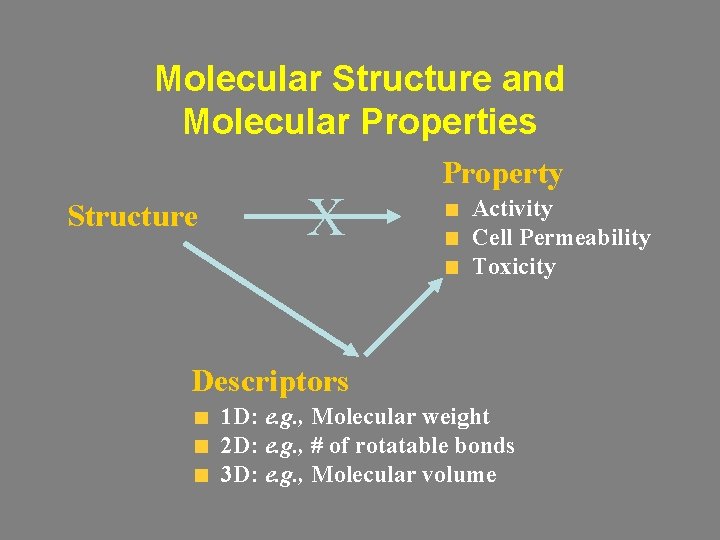
Molecular Structure and Molecular Properties Structure Property Activity Cell Permeability Toxicity Descriptors 1 D: e. g. , Molecular weight 2 D: e. g. , # of rotatable bonds 3 D: e. g. , Molecular volume

Molecular mechanics

Introduction to Force Fields

Molecular mechanics • Ball and spring description of molecules • Better representation of equilibrium geometries than plastic models • Able to compute relative strain energies • Cheap to compute • Lots of empirical parameters that have to be carefully tested and calibrated • Limited to equilibrium geometries • Does not take electronic interactions into account • No information on properties or reactivity • Cannot readily handle reactions involving the making and breaking of bonds

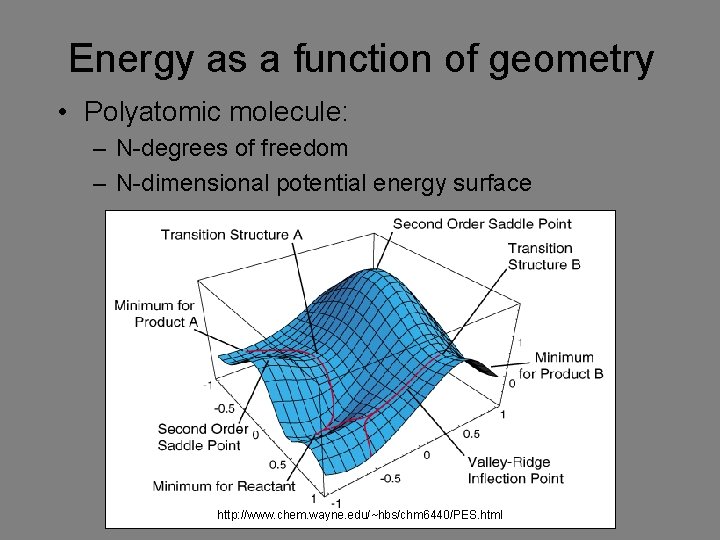
Energy as a function of geometry • Polyatomic molecule: – N-degrees of freedom – N-dimensional potential energy surface http: //www. chem. wayne. edu/~hbs/chm 6440/PES. html

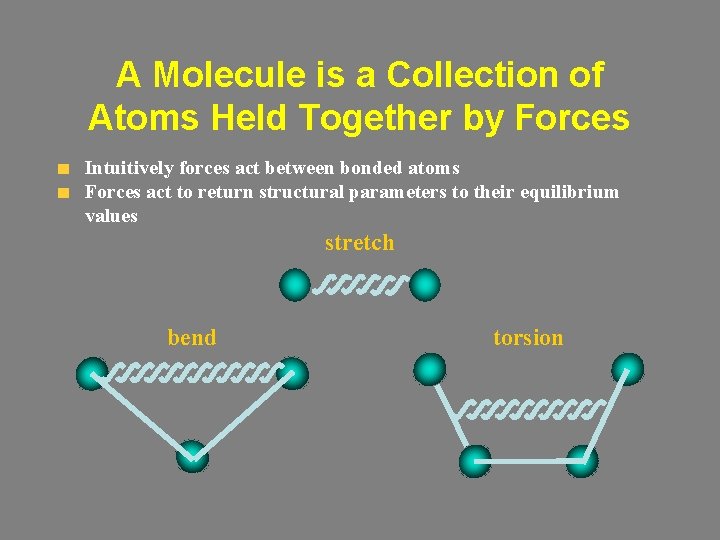
A Molecule is a Collection of Atoms Held Together by Forces Intuitively forces act between bonded atoms Forces act to return structural parameters to their equilibrium values stretch bend torsion

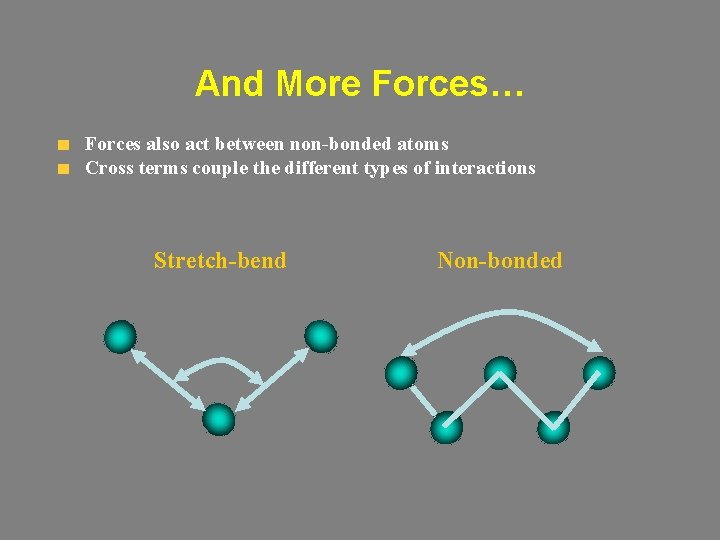
And More Forces… Forces also act between non-bonded atoms Cross terms couple the different types of interactions Stretch-bend Non-bonded

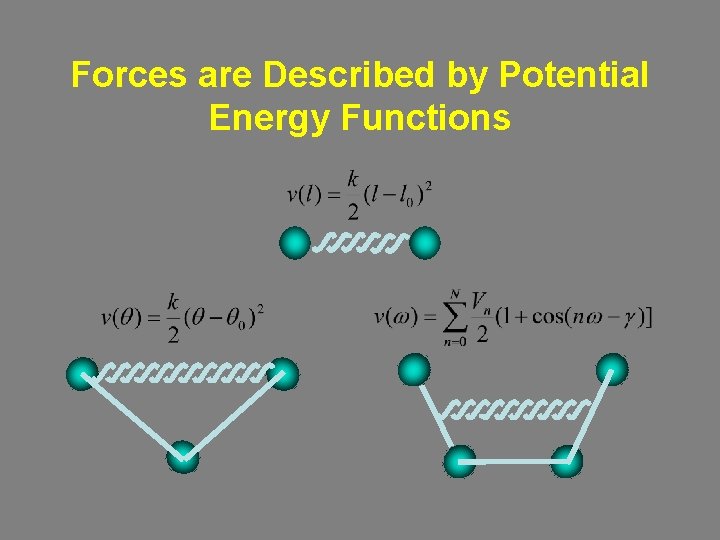
Forces are Described by Potential Energy Functions

And More Functions…

A Force Field is a Collection of Potential Energy Functions A force field is defined by the functional forms of the energy functions and by the values of their parameters.

Molecular Mechanics Energy (Steric Energy) is Calculated from the Force Field A molecular mechanics program will return an energy value for every conformation of the system. Steric energy is the energy of the system relative to a reference point. This reference point depends on the bonded interactions and is both force field dependent and molecule dependent. Thus, steric energy can only be used to compare the relative stabilities of different conformations of the same molecule and can not be used to compare the relative stabilities of different molecules. Further, all conformational energies must be calculated with the same force field.

Steric Energy = Estretch + Ebend + Etorsion + EVd. W + Eelectrostatic + Estretch-bend + Etorsion-stretch + … Estretch Ebend Etorsion EVd. W Eelectrostatic Estretch-bend Etorsion-stretch Stretch energy (over all bonds) Bending energy (over all angles) Torsional (dihedral) energy (over all dihedral angles) Van Der Waals energy (over all atom pairs > 1, 3) Electrostatic energy (over all charged atom pairs >1, 3) Stretch-bend energy Torsion-stretch energy EVd. W + Eelectrostatic are often referred to as non-bonded energies

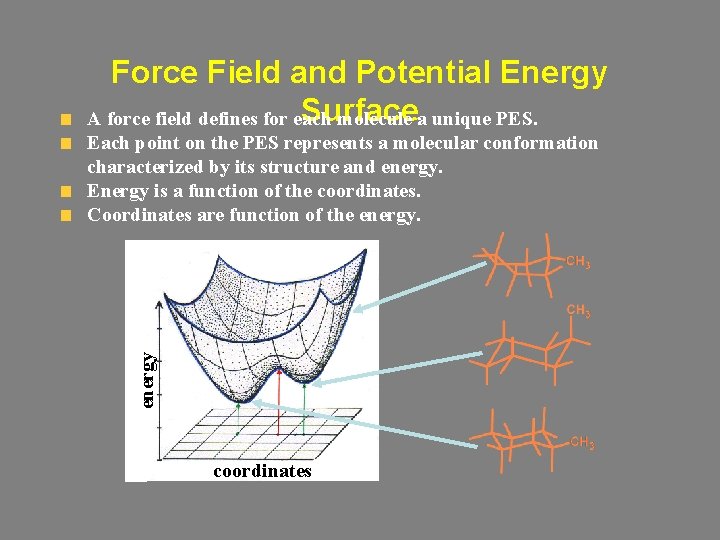
Force Field and Potential Energy Surface A force field defines for each molecule a unique PES. energy Each point on the PES represents a molecular conformation characterized by its structure and energy. Energy is a function of the coordinates. Coordinates are function of the energy. coordinates

Moving on (Sampling) the PES Each point on the PES is represents a molecular conformation characterized by its structure and energy. By sampling the PES we can derive molecular properties. Sampling energy minima only (energy minimization) will lead to molecular properties reflecting the enthalpy only. Sampling the entire PES (molecular simulations) will lead to molecular properties reflecting the free energy. In both cases, molecular properties will be derived from the PES.

Force Fields: General Features Force field definition • Functional form (usually a compromise between accuracy and ease of calculation. • Parameters (transferability assumed). Force fields are empirical • There is no “correct” form of a force field. • Force fields are evaluated based solely on their performance. Force field are parameterized for specific properties • Structural properties • Energy • Spectra

Force Fields: Atom Types In molecular mechanics atoms are given types - there are often several types for each element. Atom types depend on: • Atomic number (e. g. , C, N, O, H). • Hybridization (e. g. , SP 3, SP 2, SP). • Environment (e. g. , cyclopropane, cyclobutane). MM 2 type 2 C O C C MM 2 type 3 “Transferability” is assumed - for example that a C=O bond will behave more or less the same in all molecules.

A General Force Field Calculation Input • Atom Types • Starting geometry • Connectivity Energy minimization / geometry optimization Calculate molecular properties at final geometry Output • • Molecular structure Molecular energy Dipole moments etc.

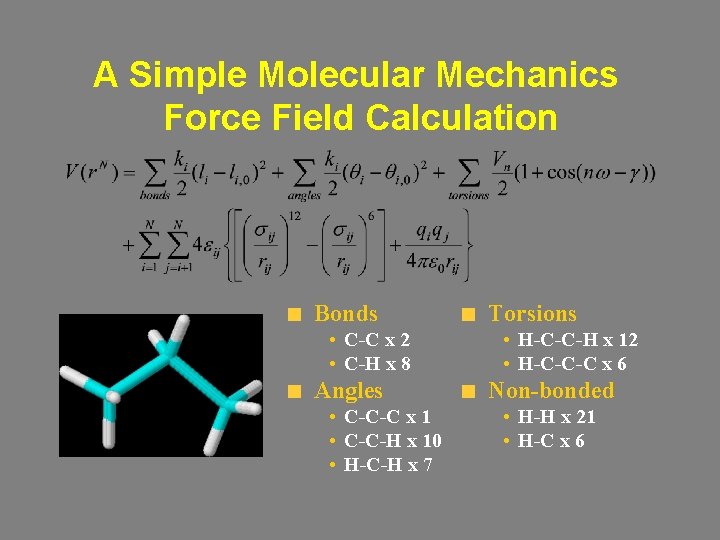
A Simple Molecular Mechanics Force Field Calculation Bonds • C-C x 2 • C-H x 8 Angles • C-C-C x 1 • C-C-H x 10 • H-C-H x 7 Torsions • H-C-C-H x 12 • H-C-C-C x 6 Non-bonded • H-H x 21 • H-C x 6

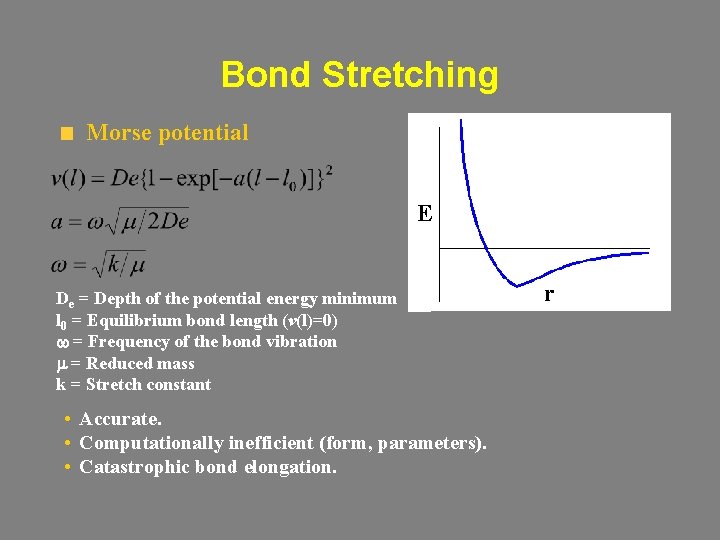
Bond Stretching Morse potential E De = Depth of the potential energy minimum l 0 = Equilibrium bond length (v(l)=0) w = Frequency of the bond vibration m = Reduced mass k = Stretch constant • Accurate. • Computationally inefficient (form, parameters). • Catastrophic bond elongation. r

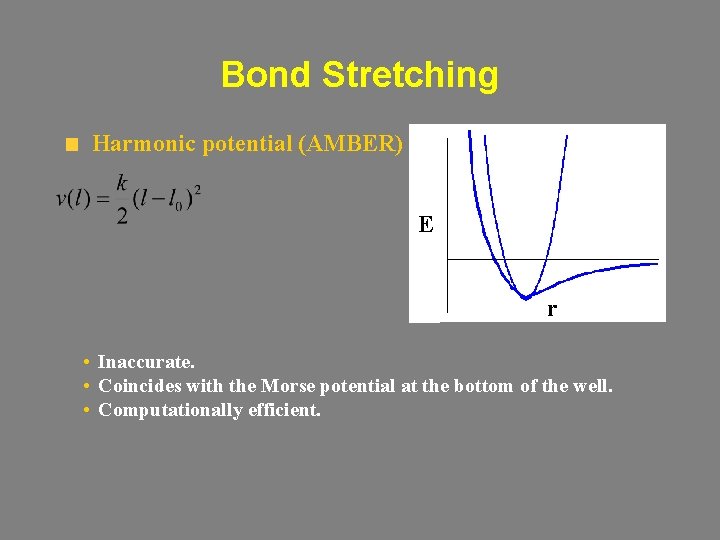
Bond Stretching Harmonic potential (AMBER) E r • Inaccurate. • Coincides with the Morse potential at the bottom of the well. • Computationally efficient.

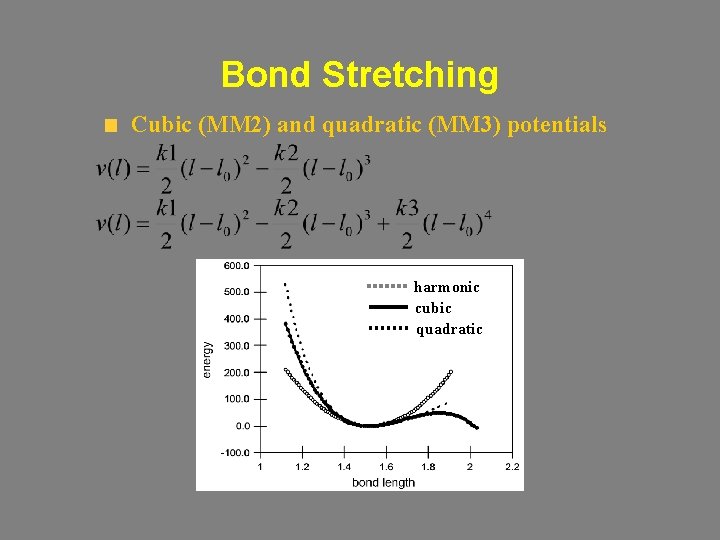
Bond Stretching Cubic (MM 2) and quadratic (MM 3) potentials harmonic cubic quadratic

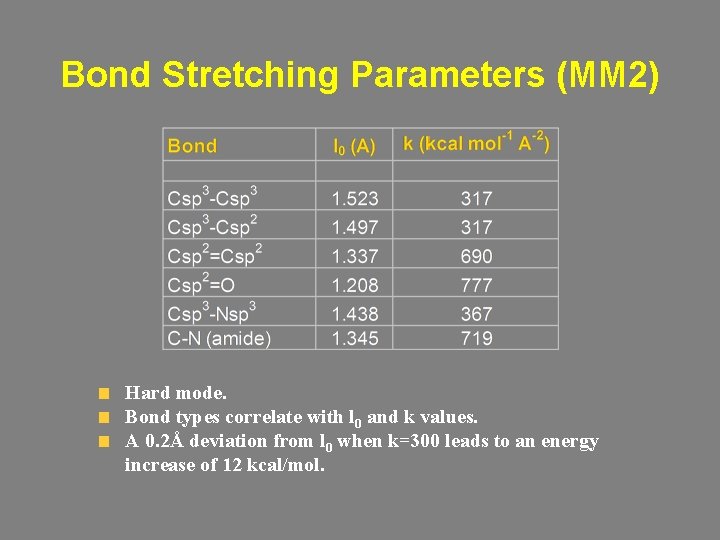
Bond Stretching Parameters (MM 2) Hard mode. Bond types correlate with l 0 and k values. A 0. 2Å deviation from l 0 when k=300 leads to an energy increase of 12 kcal/mol.

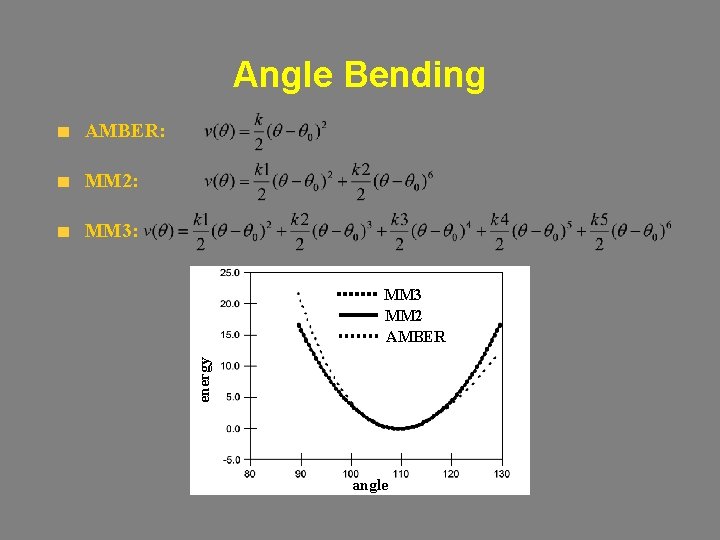
Angle Bending AMBER: MM 2: MM 3: energy MM 3 MM 2 AMBER angle

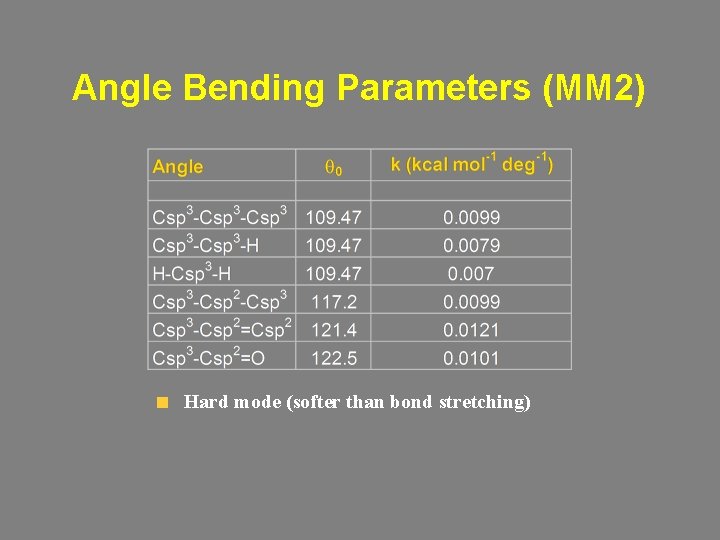
Angle Bending Parameters (MM 2) Hard mode (softer than bond stretching)

Torsional (Dihedral) Terms Reflect the existence of barriers to rotation around chemical bonds. Used to set the relative energies of the rotational minima and maxima. Together with the non-bonded terms are responsible for most of the structural and energetic changes (soft mode). Usually parameterized last. Soft mode.

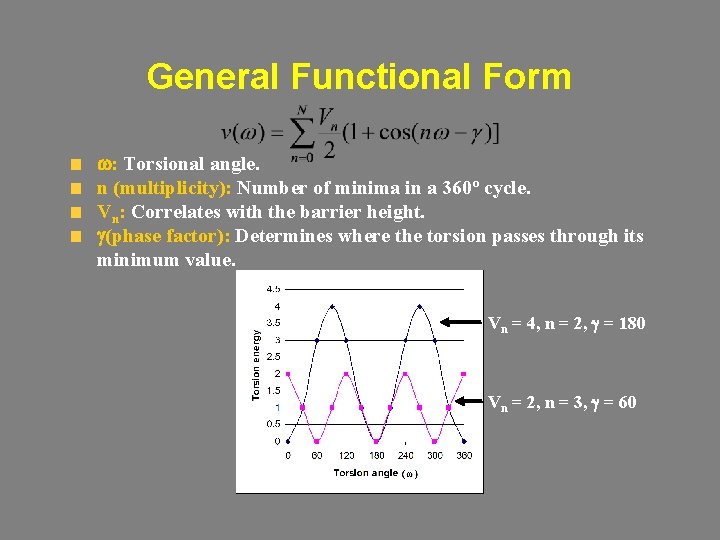
General Functional Form w: Torsional angle. n (multiplicity): Number of minima in a 360º cycle. Vn: Correlates with the barrier height. g(phase factor): Determines where the torsion passes through its minimum value. Vn = 4, n = 2, g = 180 Vn = 2, n = 3, g = 60

Functional Form: AMBER Preference to single terms. Usage of general torsional parameters (i. e. , torsional potential solely depends on the two central atoms of the torsion). • C-C-C-C = O-C-C-N = …

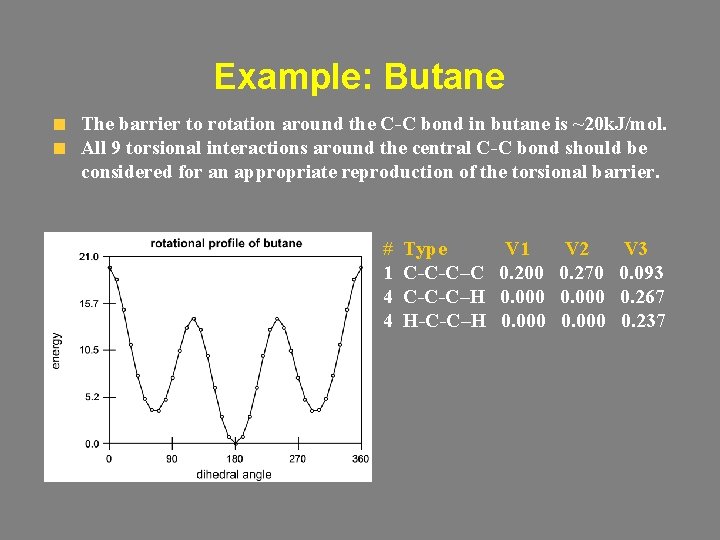
Example: Butane The barrier to rotation around the C-C bond in butane is ~20 k. J/mol. All 9 torsional interactions around the central C-C bond should be considered for an appropriate reproduction of the torsional barrier. # 1 4 4 Type C-C-C–C C-C-C–H H-C-C–H V 1 0. 200 0. 000 V 2 0. 270 0. 000 V 3 0. 093 0. 267 0. 237

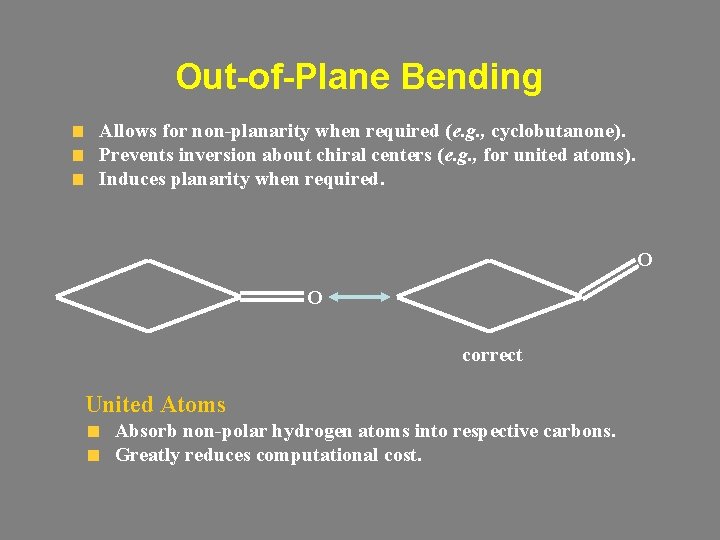
Out-of-Plane Bending Allows for non-planarity when required (e. g. , cyclobutanone). Prevents inversion about chiral centers (e. g. , for united atoms). Induces planarity when required. O O correct United Atoms Absorb non-polar hydrogen atoms into respective carbons. Greatly reduces computational cost.

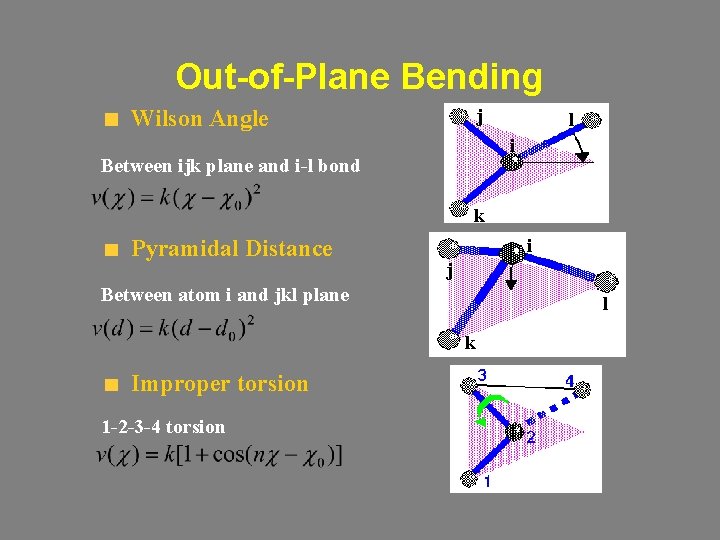
Out-of-Plane Bending j Wilson Angle l i Between ijk plane and i-l bond k Pyramidal Distance i j Between atom i and jkl plane l k Improper torsion 1 -2 -3 -4 torsion

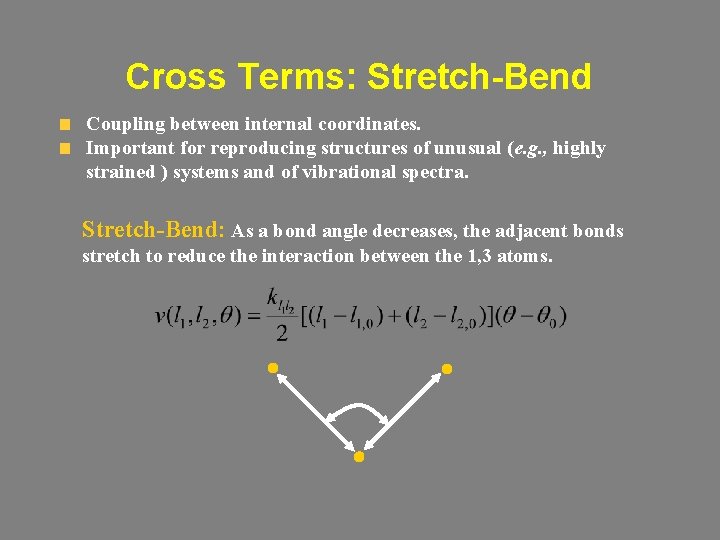
Cross Terms: Stretch-Bend Coupling between internal coordinates. Important for reproducing structures of unusual (e. g. , highly strained ) systems and of vibrational spectra. Stretch-Bend: As a bond angle decreases, the adjacent bonds stretch to reduce the interaction between the 1, 3 atoms.

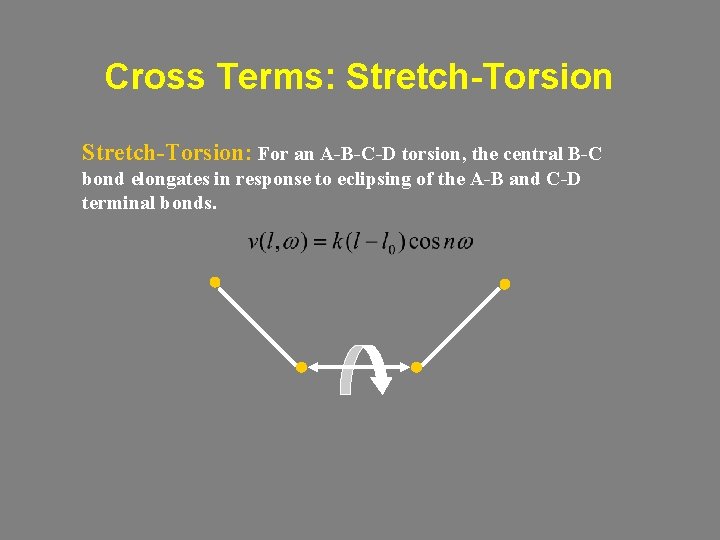
Cross Terms: Stretch-Torsion: For an A-B-C-D torsion, the central B-C bond elongates in response to eclipsing of the A-B and C-D terminal bonds.

Non-Bonded Interactions Operate within molecules and between molecules. Through space interactions. Modeled as a function of an inverse power of the distance. Soft mode. Divided into: • Electrostatic interactions. • Vd. W interactions.

Electrostatic Interactions qi, qj are point charges. Charge-charge interactions are long ranged (decay as r-1). When qi, qj are centered on the nuclei they are referred to as partial atomic charges. • Fit to known electric moments (e. g. , dipole, quadrupole etc. ) • Fit to thermodynamic properties. • Ab initio Calculations – Electrostatic potential

Rapid Methods for Calculating Atomic Charges Partial Equalization of Orbital Electronegativity (Gasteiger and Marsili) http: //www 2. chemie. uni-erlangen. de/software/petra/manual. pdf Electronegativity (Pauling): “The power of an atom to attract an electron to itself” Orbital electronegativity depends upon: • Valence state (e. g. , sp > sp 3). • Occupancy (e. g. , empty > single > double). • Charges in other orbitals. Electrons flow from the less electronegative atoms to the more electronegative atoms thereby equalizing the electronegativities.

Partial Equalization of Orbital Electronegativity For the dependency of orbital electronegativity on charge assume: Theoretically correct for orbitals but formally applied to atoms. Values of a, b and c were obtained for common elements in their usual valence states (e. g. , for atom types). Apply an interactive process: • Assign each atom its formal charge. • Calculate atomic electronegativities based on above assumption. • Calculate the electron charge transferred from atom A to the more electronegative atom B bonded to it by: Dumping factor Cation Electronegativity of the less electronegative atom

Solvent Dielectric Models e 0 = Dielectric constant of vacuum (1). For a given set of charges and distance, e 0 determines the strength of the electrostatic interactions. Solvent effect dampen the electrostatic interactions and so can be modeled by varying e 0: · eeff = e 0 er · er(protein interior) = 2 -4 · er(water) = 80

Solvent Dielectric Models: Distance Dependence Dielectric constant increases as a function of distance eeff Smooth increase in eeff form 1 to er as the distance increases distance eeff varies from 1 at zero separation to the bulk permitivity of the solvent at large separation. As the separation between the interacting atoms increases, more solvent can “penetrate” between them.

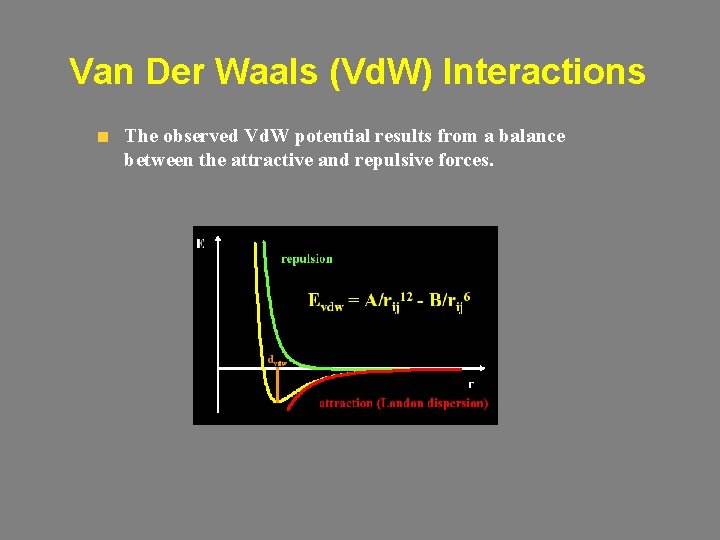
Van Der Waals (Vd. W) Interactions Electrostatic interactions can’t account for all non-bonded interactions within a system (e. g. , rare gases). Vd. W interactions: • Attractive (dispersive) contribution (London forces) – Instantaneous dipoles due to electron cloud fluctuations. – Decays as r 6. • Repulsive contribution – Nuclei repulsion. – At short distances (r < 1) rises as 1/r. – At large distances decays as exp(-2 r/a 0); a 0 the Bohr radius.

Van Der Waals (Vd. W) Interactions The observed Vd. W potential results from a balance between the attractive and repulsive forces.

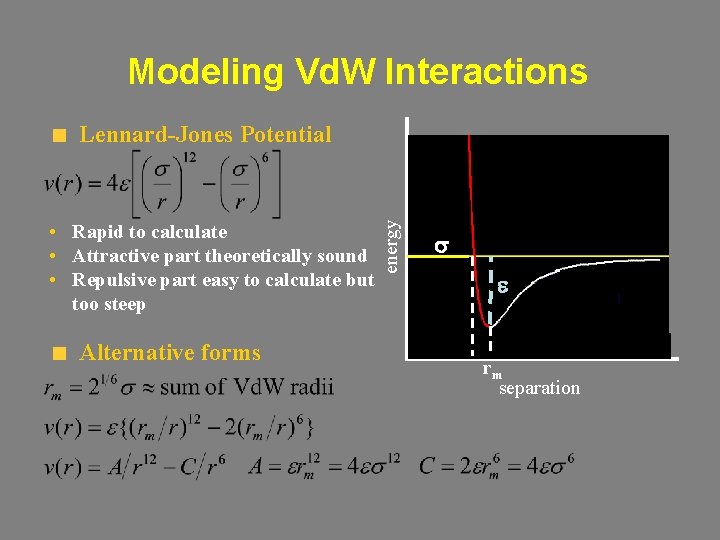
Modeling Vd. W Interactions • Rapid to calculate • Attractive part theoretically sound • Repulsive part easy to calculate but too steep Alternative forms energy Lennard-Jones Potential s e rm separation

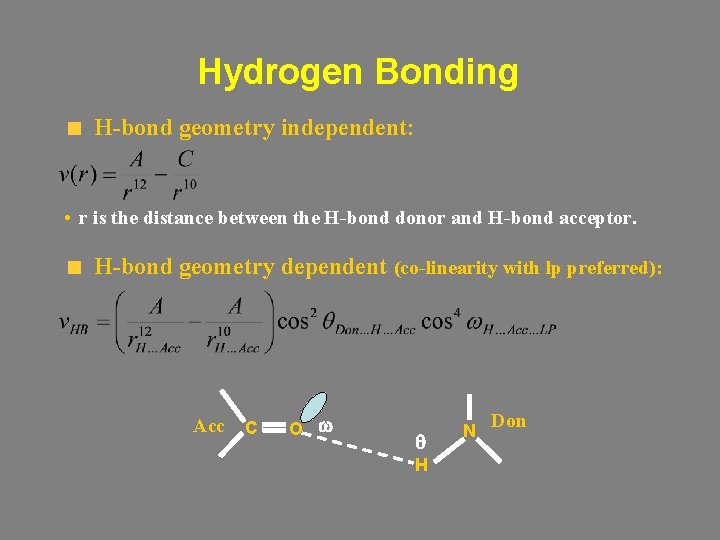
Hydrogen Bonding H-bond geometry independent: • r is the distance between the H-bond donor and H-bond acceptor. H-bond geometry dependent (co-linearity with lp preferred): Acc C O w q H N Don

Force Field Parameterization Choosing values for the parameters in the potential function equations to best reproduce experimental data. Parameterization techniques • Trial and error • Least square methods Types of parameters • • • Stretch: natural bond length (l 0) and force constants (k). Bend: natural bond angles (q 0) and force constants (k). Torsions: Vi’s. Vd. W: (e, Vd. W radii). Electrostatic: Partial atomic charges. Cross-terms: Cross term parameters.

Parameters - Quantity For N atom types require: • • N non-bonded parameters N*N stretch parameters N*N*N bend parameters N*N*N*N torsion parameters Example Macro. Model MM 2*: 39 atom types Stretch Bend Torsion Required 1521 58, 319 2, 313, 441 Actual 164 357 508

Parameters - Source A force field parameterized according to data from one source (e. g. , experimental gas phase, experimental solid phase, ab initio) will fit data from other sources only qualitatively. Experiment: geometries and non-bonded parameters • • X-Ray crystallography Electron diffraction Microwave spectroscopy Lattice energies Advantages • Real Disadvantages • Hard to obtain • Non-uniform • Limited availability

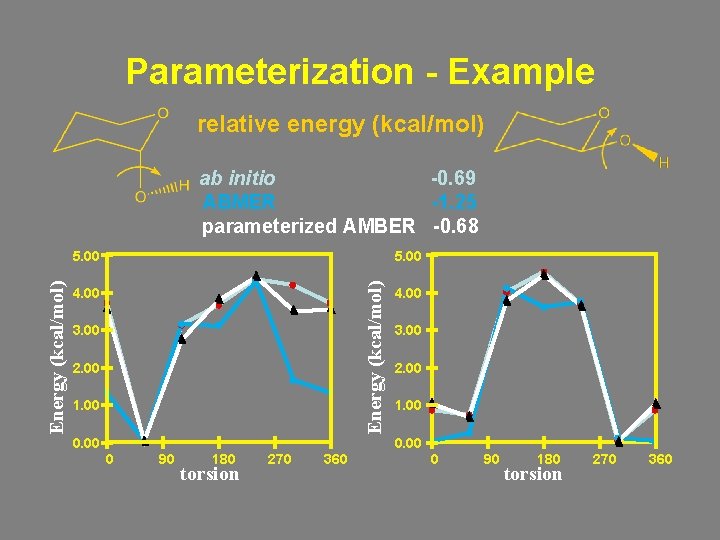
Parameterization - Example relative energy (kcal/mol) ab initio -0. 69 ABMER -1. 25 parameterized AMBER -0. 68 5. 00 Energy (kcal/mol) 5. 00 4. 00 3. 00 2. 00 1. 00 0 90 180 torsion 270 360

Transferability of Parameters Assumption: The same set of parameters can be used to model a related series of compounds: • Prediction • Missing parameters – Educated guess – Parameters derived from atomic properties (e. g. , UFF) • Reducing number of parameters – Generalized torsions (e. g. , depend only on two central atoms) – Generalized Vd. W parameters (same for SP, SP 2, SP 3) Above assumption breaks down for close interaction function groups: O X O O

Existing Force Fields AMBER (Assisted Model Building with Energy Refinement) • Parameterized specifically for proteins and nucleic acids. • Uses only 5 bonding and non-bonding terms along with a sophisticated electrostatic treatment. • No cross terms are included. • Results can be very good for proteins and nucleic acids, less so for other systems. CHARMM (Chemistry at Harvard Macromolecular Mechanics) • Originally devised for proteins and nucleic acids. • Now used for a range of macromolecules, molecular dynamics, solvation, crystal packing, vibrational analysis and QM/MM studies. • Uses 5 valence terms, one of which is electrostatic term. • Basis for other force fields (e. g. , MOIL).

Existing Force Fields GROMOS (Gronigen molecular simulation) • Popular for predicting the dynamical motion of molecules and bulk liquids. • Also used for modeling biomolecules. • Uses 5 valence terms, one of which is an electrostatic term. MM 1, 2, 3, 4 • General purpose force fields for (mono-functional) organic molecules. • MM 2 was parameterized for a lot of functional groups. • MM 3 is probably one of the most accurate ways of modeling hydrocarbons. • MM 4 is very new and little is known about its performance. • The force fields use 5 to 6 valence terms, one of which is an electrostatic term and one to nine cross terms.

Existing Force Fields MMFF (Merck Molecular Force Field) • General purpose force fields mainly for organic molecules. • MMFF 94 was originally designed for molecular dynamics simulations but is also widely used for geometry optimization. • Uses 5 valence terms, one of which is an electrostatic term and one cross term. • MMFF was parameterized based on high level ab initio calculations. OPLS (Optimized Potential for Liquid Simulations) • Designed for modeling bulk liquids. • Has been extensively used for modeling the molecular dynamics of biomolecules. • Uses 5 valence terms, one of which is an electrostatic term but no cross terms.

Existing Force Fields Tripos (SYBYL force field) • Designed for modeling organic and biomolecules. • Often used for Co. MFA analysis (QSAR method). • Uses 5 valence terms, one of which is an electrostatic term. MOMEC • A force field for describing transition metals coordination compounds. • Originally parameterized to use 4 valence terms but not an electrostatic term. • Metal-ligand interactions consist of bond stretch only. • Coordination sphere is maintained by non-bonding interactions between ligands. • Work reasonable well for octahedrally coordinated compounds.

Existing Force Fields UFF (Universal Force Field) • Designed for coverage of the entire periodic table. • All force field parameters are atomic based. • Parameters for specific interactions are derived from atomic parameters based on a series of mixing rules, thereby addressing the problem of parameter explosion. • Uses 4 valence terms but not an electrostatic term. YATI • Designed for the accurate representation of non-bonded interactions. • Most often used for modeling interactions between biomolecules and small substrate molecules.

Existing Force Fields CVFF (Consistent Valence Force Field) • Parameterized for small organic (amides, carboxylic acids, etc. ) crystals and gas phase structures. • Handles peptides, proteins, and a wide range of organic systems. • Primarily intended for studies of structures and binding energies, although it predicts vibrational frequencies and conformational energies reasonably well.

Existing Force Fields CFF, CFF 91, CFF 95 (Consistent Force Field) • Parameterized (based on quantum mechanics calculations and molecular simulations) for acetals, acids, alcohols, alkanes, alkenes, amides, amines, aromatics, esters, and ethers. • Useful for predicting: – Small molecules: gas-phase geometries, vibrational frequencies, conformational energies, torsion barriers, crystal structures. – Liquids: cohesive energy densities; for crystals: lattice parameters, RMS atomic coordinates, sublimation energies. – Macromolecules: protein crystal structures, polycarbonates and polysaccharides (CFF 91, 95).

Existing Force Fields Dreiding • Parameters derived by a rule based approach. • Good coverage of the periodic table. • Good coverage for organic, biological and main-group inorganic molecules. • Only moderately accurate for geometries, conformational energies, intermolecular binding energies, and crystal packing.

Energy Minimization

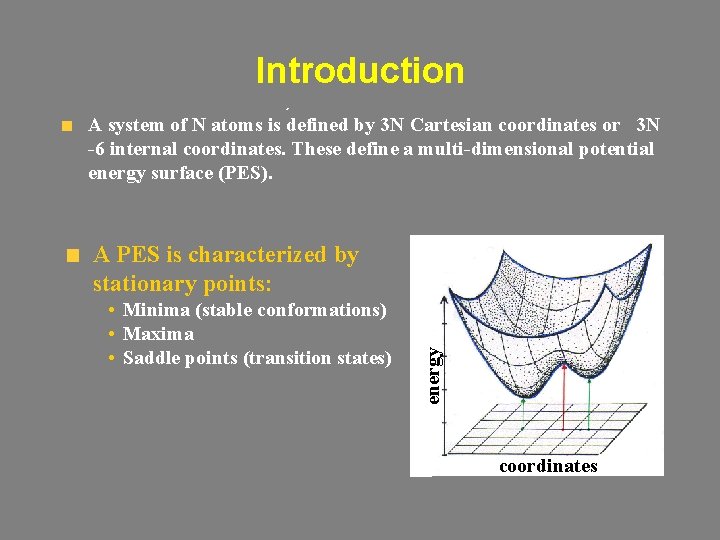
Introduction A system of N atoms is defined by 3 N Cartesian coordinates or 3 N -6 internal coordinates. These define a multi-dimensional potential energy surface (PES). • Minima (stable conformations) • Maxima • Saddle points (transition states) energy A PES is characterized by stationary points: coordinates

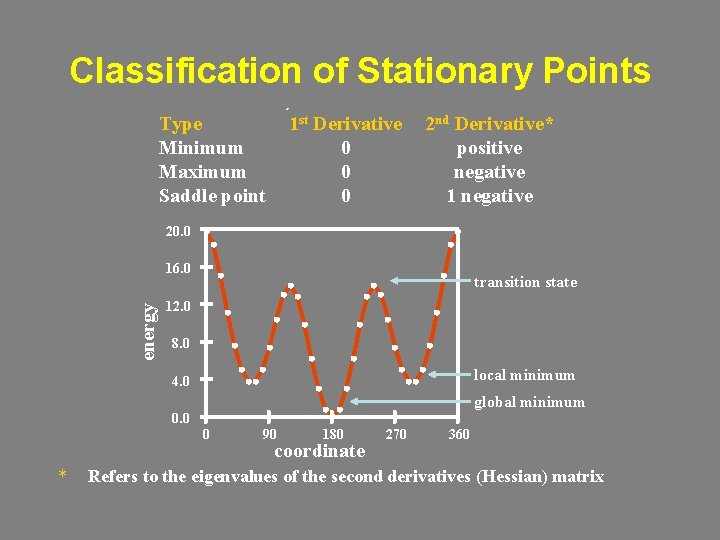
Classification of Stationary Points Type Minimum Maximum Saddle point 1 st Derivative 0 0 0 2 nd Derivative* positive negative 1 negative 20. 0 energy 16. 0 transition state 12. 0 8. 0 local minimum 4. 0 global minimum 0. 0 0 * 90 180 coordinate 270 360 Refers to the eigenvalues of the second derivatives (Hessian) matrix

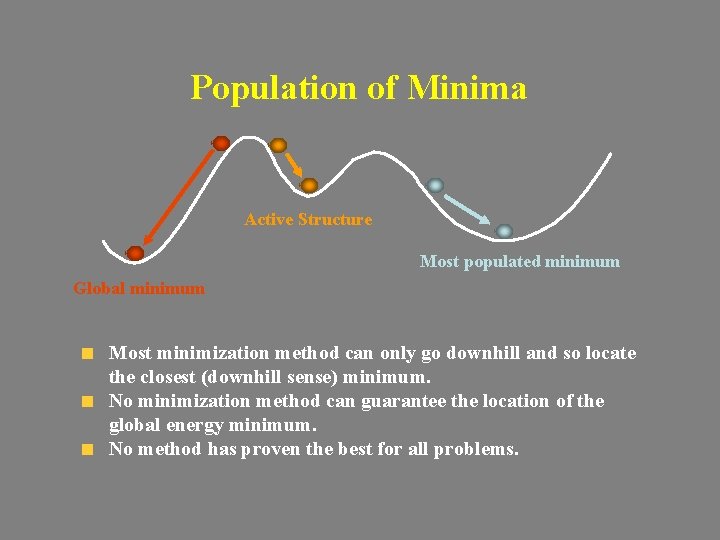
Population of Minima Active Structure Most populated minimum Global minimum Most minimization method can only go downhill and so locate the closest (downhill sense) minimum. No minimization method can guarantee the location of the global energy minimum. No method has proven the best for all problems.

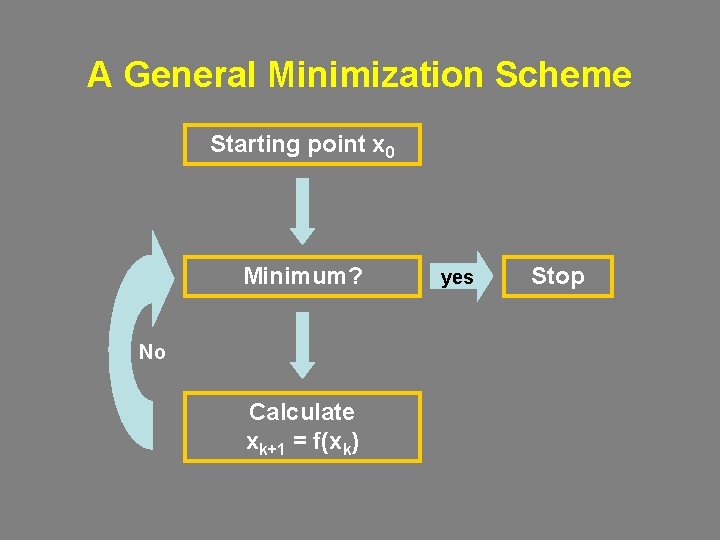
A General Minimization Scheme Starting point x 0 Minimum? No Calculate xk+1 = f(xk) yes Stop

Sequential Univariate Method For each coordinate: • Generate two new points (xi+dxi, xi+2 dxi) and calculate their energies. • Fit a parabola to xi (1), xi+dxi (2), xi+2 dxi (3) and locate its minimum (4). • Set the coordinate of xi to the parabola minimum. • When the change in all coordinates is small enough, stop. This method requires fewer function evaluations than the Simplex method but is still slow to converge.

Summary Simplex, Sequential Univariate (memory requirements scale as N) • Robust (i. e. , can be initiated from poor starting geometries). • Slow to converge even on quadratic surfaces. • Require many function evaluations (especially Simplex). Steepest Descent (memory requirements scale as 3 N) • Robust. • Convergence guaranteed on quadratic surfaces. • Slow to converge especially near the minimum. Conjugate gradient, Quasi NR (memory requirements scale as (3 N)2) • Converges in approximately N steps for N degrees of freedom. • Convergence guaranteed on quadratic surfaces. • Unstable away from the minimum (i. e. , when surface not quadratic). • CG is the method of choice for large systems. Newton-Raphson (memory requirements scale as (3 N)2) • Converges in one step on quadratic surfaces. • Unstable away from the minimum. • Computationally expensive.