Mole Conversions The mole is the basic SI

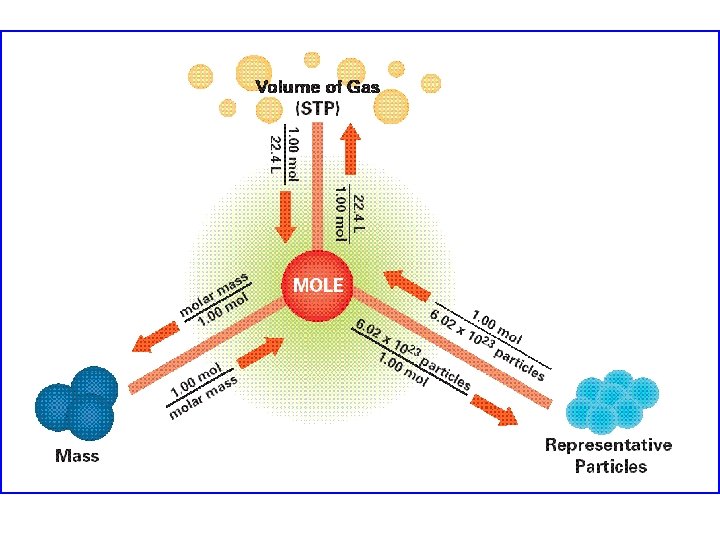
Mole Conversions The mole is the basic SI unit of quantity and is equal to 6. 02 × 1023 of anything. Here are the useful mole conversions used in chemistry… Particles (atoms, ion, molecules, etc): 1 mole = 6. 02 × 1023 particles Mass (grams, etc): 1 mole = molar mass (mass of 6. 02 × 1023 particles) Volume (liters, etc): 1 mole = 22. 4 L at STP (273 K and 101. 3 k. Pa) The molar mass and formula mass for a compound are found in the same manner…simply add up the mass contributed by each element in the compound (found by multiplying each element’s atomic mass by the number present). If you are referring to a single molecule or ion the mass is in amu’s and is the formula mass. If you are referring to one mole (6. 02 × 1023) of the molecule or ions then the mass is in grams and is the molar mass. Mole conversions follow basic dimensional analysis rules and are part of nearly all meaningful stoichiometric calculations.

Example 1 - Particles Determine the number of oxygen atoms in 3. 65 mol of oxygen gas (O 2).

Example 2 - Mass How many moles of iron(II) chloride (Fe. Cl 2) do I have if I mass out 45. 2 g of the substance?

Example 4 – Determine the mass of 55. 8 L of xenon dioxide gas at STP. Example 5 – Determine the number of iron atoms in 75 g of iron(III) oxide.

Basic Stoichiometry 1. Write the BCE for the chemical reaction. 2. Write down the given quantity and convert its quantity to moles if needed. 3. Use the mole ration from the BCE to covert from moles of the given material to moles of the sought material. 4. Convert the number of moles of the sought material to any other quantity desired using a mole conversion. 5. Does your answer make sense?

EXAMPLE 1 Determine the mass of sodium chloride that can be produced when 125. 2 L of chlorine gas at STP is reacted with excess sodium metal.

Limiting and Excess Reactants 1. Convert the known quantities to moles if required. 2. Divide each number of moles by the corresponding coefficient in the BCE to obtain the “reaction multiplier”. 3. The chemical species with the smallest “reaction multiplier” is the limiting reactant. 4. ALL OF THE LIMITING REACTANT IS CONSUMED AND ITS AMOUNT DETERMINES THE AMOUNTS OF ALL OTHER SPECIES USED OR PRODUCED!!! 5. The chemical species with the greatest “reaction multiplier” is the excess reactant. 6. SOME OF THE EXCESS REACTANT REMAINS AFTER THE REACTION IS COMPLETED!!

EXAMPLE 2 314. 2 L of nitrogen gas at STP is mixed with 80. 0 g of hydrogen gas in a reactor. This process, known as the Haber process, can be driven to completion by removal of the product (ammonia). Determine the limiting and excess reactants in this process.

EXAMPLE 2 314. 2 L of nitrogen gas at STP is mixed with 80. 0 g of hydrogen gas in a reactor. This process, known as the Haber process, can be driven to completion by removal of the product (ammonia). Determine the limiting and excess reactants in this process. Completes reaction more times, so is the EXCESS REACTANT Completes reaction fewer times, so is the LIMITING REACTANT

Theoretical and Percent Yields Theoretical Yields ONLY depend on the LIMITING REACTANT! Use basic stoichiometry from limiting reactant to desired product. Percent Yields are affected by many factors. They are calculated similarly to grades, where theoretical yield is considered 100%. These values can be less than, equal to, or greater than 100%

EXAMPLE 3 a 10. 5 g of lithium metal reacts with 25 g of red phosphorous (P 4) to create lithium phosphide. Determine the Percent yield of the process if 15 g of product is produced.

EXAMPLE 3 a (alternative method) 10. 5 g of lithium metal reacts with 25 g of red phosphorous (P 4) to create lithium phosphide. Determine the Percent yield of the process if 15 g of product is produced.

EXAMPLE 3 b 13. 6 g of hydrogen gas reacts with 200 g of chlorine gas to produce hydrogen chloride. Determine the mass of excess reactant remaining if the reaction produces the maximum amount of product possible.

EXAMPLE 3 b (another alternative) 13. 6 g of hydrogen gas reacts with 200 g of chlorine gas to produce hydrogen chloride. Determine the mass of excess reactant remaining if the reaction produces the maximum amount of product possible.