Moist Adiabatic Processes Prof Fred Remer University of

Moist Adiabatic Processes Prof. Fred Remer University of North Dakota

Moist Adiabatic Processes Parcel Theory l Dry Adiabatic Process l Moist Adiabatic Process l Saturated Adiabatic Process l Pseudo Adiabatic Process l Prof. Fred Remer University of North Dakota

Moist Adiabatic Processes l Reading – Hess l Section 4. 6 – pp 51 - 58 l Equivalent Temp. – pp 63 Prof. Fred Remer University of North Dakota

Moist Adiabatic Processes l Wallace & Hobbs – pp 84 – 87 l Tsonis – pp 103 – 116 l Bohren & Albrecht – pp 287 -291 Prof. Fred Remer University of North Dakota

Moist Adiabatic Process l Objectives – Be able to identify parcel theory assumptions – Be able to state the composition of air involved in dry adiabatic processes – Be able to perform calculations using Poisson’s Equation for dry air Prof. Fred Remer University of North Dakota

Moist Adiabatic Process l Objectives – Be able to state the composition of air involved in moist adiabatic processes – Be able to perform calculations using the equation for moist adiabatic processes Prof. Fred Remer University of North Dakota

Moist Adiabatic Process l Objectives – Be able to state the composition of an air parcel involved in saturated adiabatic processes – Be able to describe the heat transfer in a parcel of air during saturated adiabatic ascent Prof. Fred Remer University of North Dakota

Moist Adiabatic Process l Objectives – Be able to state the composition of an air parcel involved in pseudo adiabatic processes – Be able to describe the heat transfer in an air parcel during pseudo adiabatic ascent Prof. Fred Remer University of North Dakota

Moist Adiabatic Process l Objectives – Be able to state the definition of equivalent potential temperature – Be able to identify conserved properties for dry and pseudo adiabatic ascent – Be able to calculate equivalent potential temperature Prof. Fred Remer University of North Dakota

Moist Adiabatic Process l Let’s review dry adiabatic processes – Parcel Theory – Poisson’s Equation Prof. Fred Remer University of North Dakota

Parcel Theory l Assumptions – Thermally insulated from its environment – Temperature changes adiabatically – Always at the same pressure as the environment at that level Prof. Fred Remer University of North Dakota Te, P Tp, P w

Parcel Theory l Assumptions – Hydrostatic equilibrium – Moving slow enough that its kinetic energy is a negligible Prof. Fred Remer University of North Dakota Te, P Tp, P w

Parcel Theory l Types of Processes – Dry Adiabatic – Moist Adiabatic – Saturated Adiabatic – Pseudo Adiabatic Prof. Fred Remer University of North Dakota

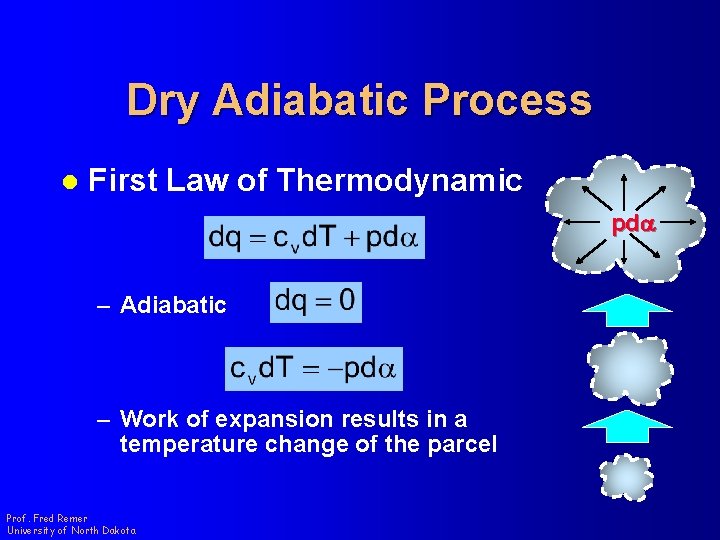
Dry Adiabatic Process l First Law of Thermodynamic pda – Adiabatic – Work of expansion results in a temperature change of the parcel Prof. Fred Remer University of North Dakota

Dry Adiabatic Process l Poisson’s Equation Prof. Fred Remer University of North Dakota

Dry Adiabatic Process l Potential Temperature Prof. Fred Remer University of North Dakota

Dry Adiabatic Process l Parcel Contains NO Moisture at All – No Water Vapor – No Liquid Water Prof. Fred Remer University of North Dakota Dry as a popcorn. . .

Dry Adiabatic Process Rising Parcel Cools at the Dry Adiabatic Lapse Rate l Potential Temperature is Constant in the Parcel l Prof. Fred Remer University of North Dakota q = const

Moist Adiabatic Process l Moist Adiabatic Process? – Dry adiabatic processes that involve water vapor Prof. Fred Remer University of North Dakota

Moist Adiabatic Process l Air is a Mixture – Dry Air l Oxygen, Nitrogen, Argon, Carbon Dioxide, etc. – Moisture l Prof. Fred Remer University of North Dakota Water Vapor

Moist Adiabatic Process Let’s look at a moist adiabatic process that involves only water vapor l Parcel Remains Unsaturated l Prof. Fred Remer University of North Dakota

Moist Adiabatic Process l Moist Adiabatic (Unsaturated) Ascent – Must include the contribution of water vapor to mixture – Adjust R/cp to account for water vapor Prof. Fred Remer University of North Dakota

Moist Adiabatic Process l Gas Constant for Mixture md = mass of dry air mv = mass of water vapor m = total mass of air Rd = Gas Constant of Dry Air Rv = Gas Constant of Water Vapor Prof. Fred Remer University of North Dakota

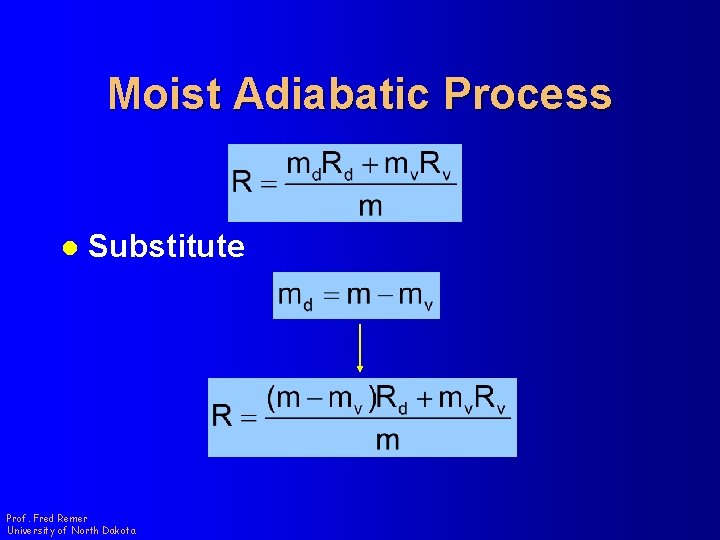
Moist Adiabatic Process l Substitute Prof. Fred Remer University of North Dakota

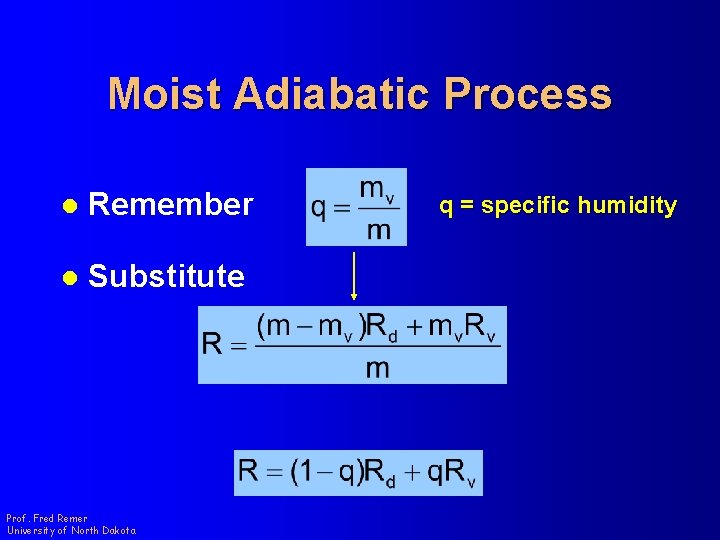
Moist Adiabatic Process l Remember l Substitute Prof. Fred Remer University of North Dakota q = specific humidity

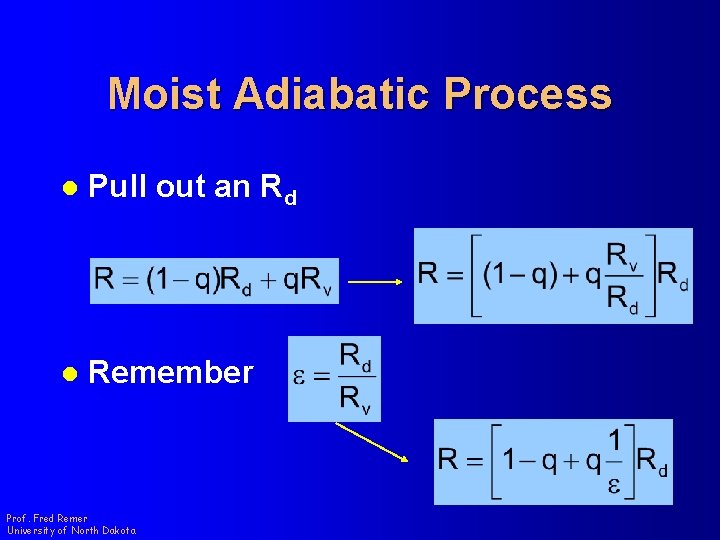
Moist Adiabatic Process l Pull out an Rd l Remember Prof. Fred Remer University of North Dakota

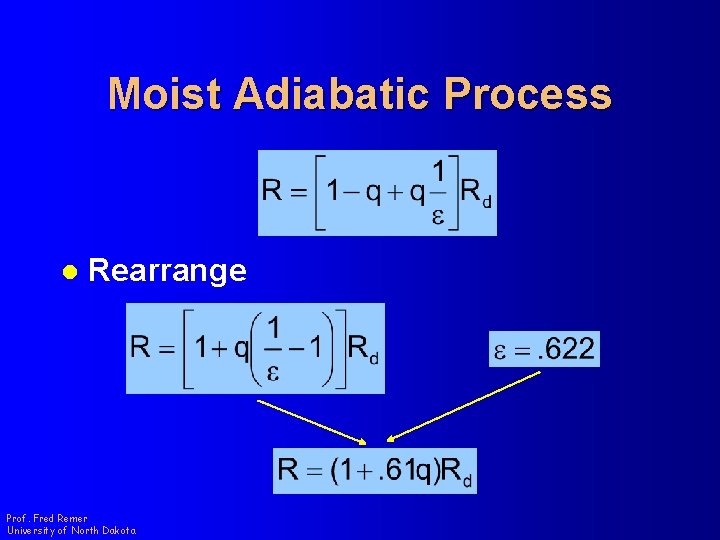
Moist Adiabatic Process l Rearrange Prof. Fred Remer University of North Dakota

Moist Adiabatic Process l Similarly, evaluate cp for the mixture – The heat absorbed to raise the temperature during an isobaric process Q = total heat qd = heat (per mass) of dry air md = mass of dry air qv = heat (per mass) of water vapor mv = mass of water vapor Prof. Fred Remer University of North Dakota

Moist Adiabatic Process l Remember l Substitute Prof. Fred Remer University of North Dakota

Moist Adiabatic Process l Divide by total mass (m) l Specific humidity (q) Prof. Fred Remer University of North Dakota

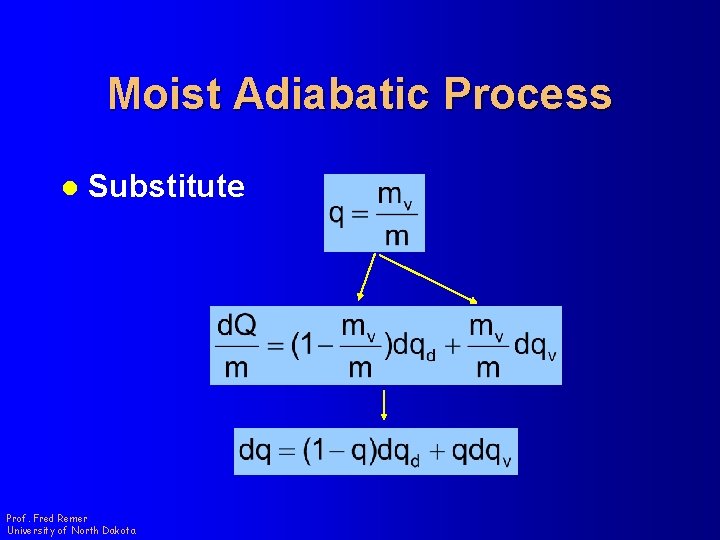
Moist Adiabatic Process l Substitute Prof. Fred Remer University of North Dakota

Moist Adiabatic Process l Divide by d. T l But … Prof. Fred Remer University of North Dakota cp = specific heat at constant pressure

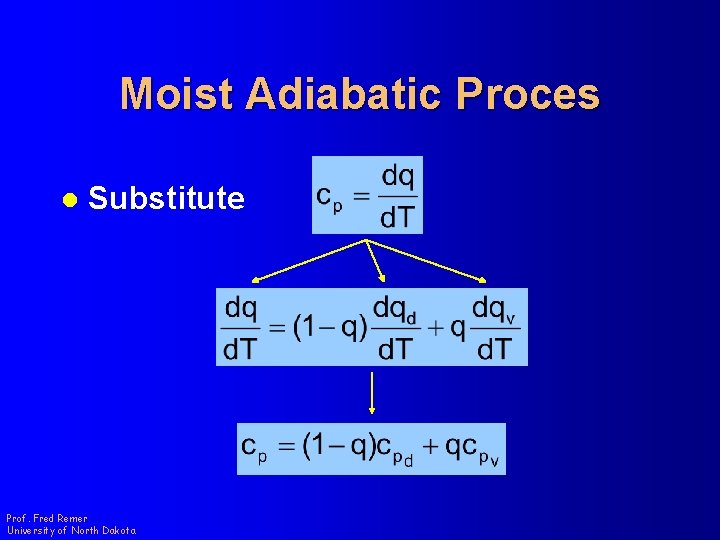
Moist Adiabatic Proces l Substitute Prof. Fred Remer University of North Dakota

Moist Adiabatic Process l Pull out cpd Prof. Fred Remer University of North Dakota

Moist Adiabatic Process l Rearrange Prof. Fred Remer University of North Dakota

Moist Adiabatic Process cpd = specific heat of dry air at constant pressure = 1004 J kg-1 K-1 cpv = specific heat of water vapor at constant pressure = 1870 J kg-1 K-1 Prof. Fred Remer University of North Dakota

Moist Adiabatic Process l Evaluate Prof. Fred Remer University of North Dakota

Moist Adiabatic Process l Now … let look at Poisson’s Equation Prof. Fred Remer University of North Dakota

Moist Adiabatic Process l Simplify using polynomial division Prof. Fred Remer University of North Dakota

Moist Adiabatic Process l Poisson’s Equation for moist, unsaturated air Prof. Fred Remer University of North Dakota

Moist Adiabatic Process l Potential Temperature for Moist, Unsaturated Air – Use 1000 mb As Reference Pressure Prof. Fred Remer University of North Dakota

Moist Adiabatic Process l Little difference between – Dry adiabatic process – Moist, unsaturated adiabatic process Prof. Fred Remer University of North Dakota

Moist Adiabatic Process l Rising Air Expands and Cools Adiabatically – Temperature Decreases – Mixing Ratio (w) is Constant l l Only depends on mass At Saturation – ws = w – Condensation – Latent Heat Release Prof. Fred Remer University of North Dakota w = ws T decr. w const.

Saturated Adiabatic Process l Now let’s consider condensation Prof. Fred Remer University of North Dakota

Saturated Adiabatic Process l Two Methods to Describe the Ascent – Saturated Adiabatic Process – Pseudoadiabatic Process Prof. Fred Remer University of North Dakota

Saturated Adiabatic Process l Latent Heat Release Will 1. Warm Air l Heterogeneous System – Dry Air – Water Vapor – Condensation Particles Prof. Fred Remer University of North Dakota

Saturated Adiabatic Process l Latent Heat Release 2. Do Work – Heating Causes Expansion Prof. Fred Remer University of North Dakota

Saturated Adiabatic Process Water Droplets Remain in Parcel l Latent Heat Remains within Parcel l Prof. Fred Remer University of North Dakota

Saturated Adiabatic Process Reversible l ‘Adiabatic’ l Isentropic l Prof. Fred Remer University of North Dakota

Saturated Adiabatic Process l Mass of System – Dry Air (md) l md Constant – Total Water (mt) Vapor (mv) l Liquid Water (mw) l m t= m t + m t Prof. Fred Remer University of North Dakota

Saturated Adiabatic Process l Condensation – Water Vapor to Liquid Water dmv Prof. Fred Remer University of North Dakota

Saturated Adiabatic Process l First Law of Thermodynamics l Latent Heat Release Prof. Fred Remer University of North Dakota

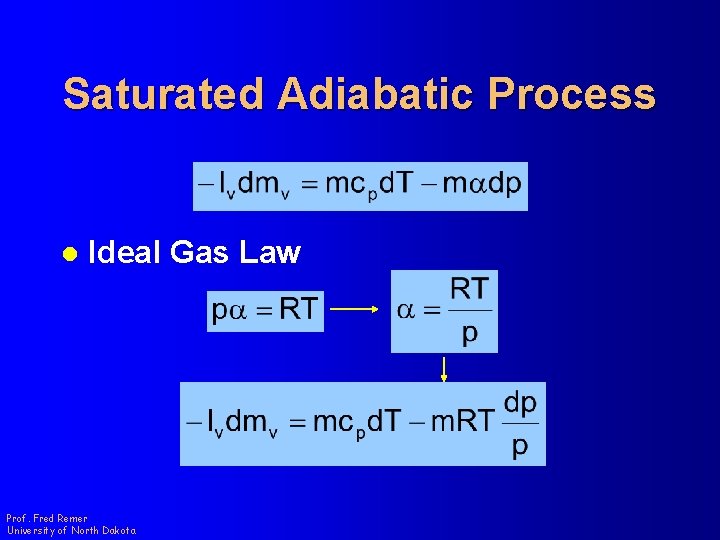
Saturated Adiabatic Process l Ideal Gas Law Prof. Fred Remer University of North Dakota

Saturated Adiabatic Process l Divide by T Prof. Fred Remer University of North Dakota

Saturated Adiabatic Process l Let’s evaluate cp, R and p l Specific Heat – Latent Heat Warms Dry Air l Water Vapor l Liquid Water l Prof. Fred Remer University of North Dakota

Saturated Adiabatic Process l Gas Constant – Dry Air – Water Vapor Prof. Fred Remer University of North Dakota

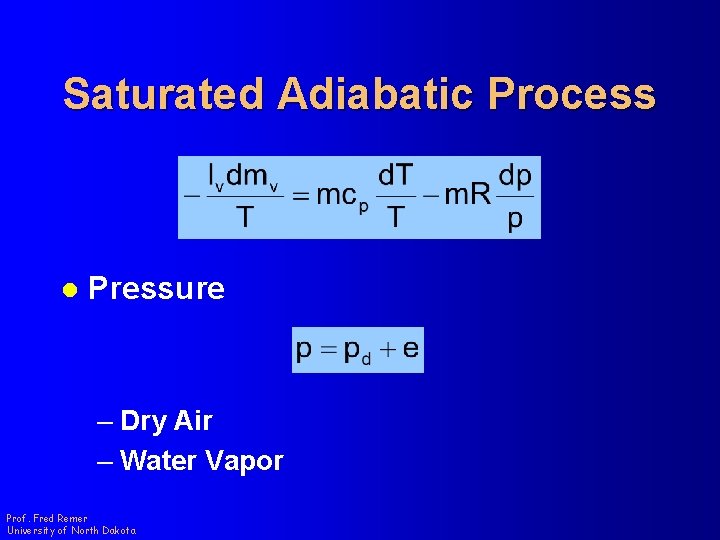
Saturated Adiabatic Process l Pressure – Dry Air – Water Vapor Prof. Fred Remer University of North Dakota

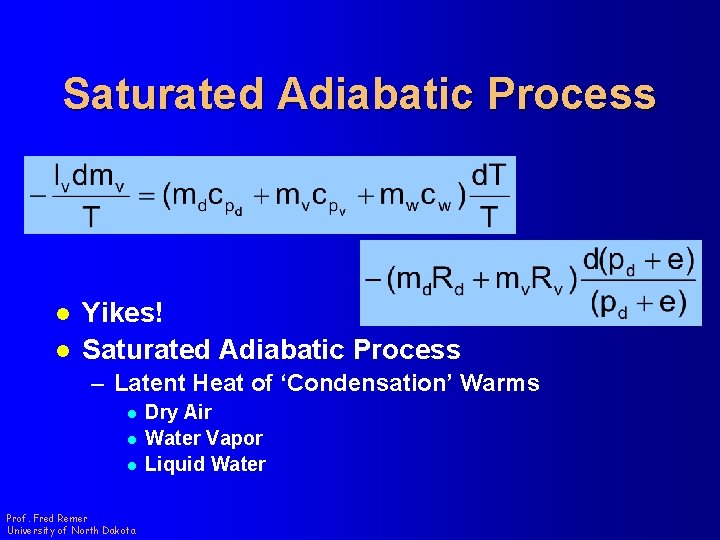
Saturated Adiabatic Process l l Yikes! Saturated Adiabatic Process – Latent Heat of ‘Condensation’ Warms l l l Prof. Fred Remer University of North Dakota Dry Air Water Vapor Liquid Water

Saturated Adiabatic Process l Assumptions – Difference Between Moist Adabatic and Dry Adiabatic Processes is Small Prof. Fred Remer University of North Dakota

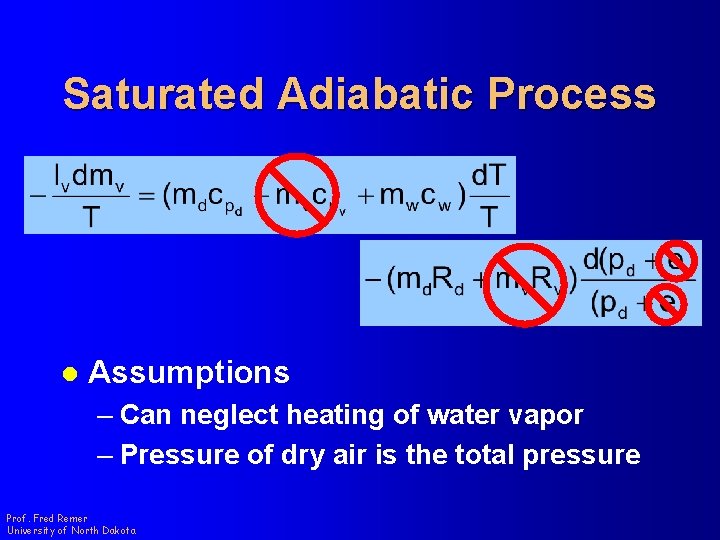
Saturated Adiabatic Process l Assumptions – Can neglect heating of water vapor – Pressure of dry air is the total pressure Prof. Fred Remer University of North Dakota

Saturated Adiabatic Process l Equation for Saturated Adiabatic Process – Ignore Heating of Water Vapor l Small Error – Liquid Water Remains with Rising Parcel Prof. Fred Remer University of North Dakota

Pseudoadiabatic Process Water Droplets Fall Out of Parcel l Latent Heat Remains within Parcel l Latent Heat Warms Only Dry Air l Prof. Fred Remer University of North Dakota

Pseudoadiabatic Process Irreversible l Pseudoadiabatic l Change in Entropy l Prof. Fred Remer University of North Dakota

Pseudoadiabatic Process l What does that do to our equation? – No water mass to heat! Prof. Fred Remer University of North Dakota

Pseudoadiabatic Process l Divide both sides by mass of dry air w = mixing ratio Prof. Fred Remer University of North Dakota

Pseudoadiabatic Process l Equation for pseudoadiabatic processes – Neglects heating of water vapor – Neglects heating of water mass – Latent heat release only warms dry air Prof. Fred Remer University of North Dakota

Pseudoadiabatic Process l Not a bad integration except for…. – Left hand side l lv = f(T) l w = f(T) Prof. Fred Remer University of North Dakota

Pseudoadiabatic Process l Assumptions – lv varies little with temperature (T) l Prof. Fred Remer University of North Dakota Valid assumption

Pseudoadiabatic Process l Assumptions – Which varies more during a pseudoadiabatic process? l dw or T? – Let’s evaluate! Prof. Fred Remer University of North Dakota

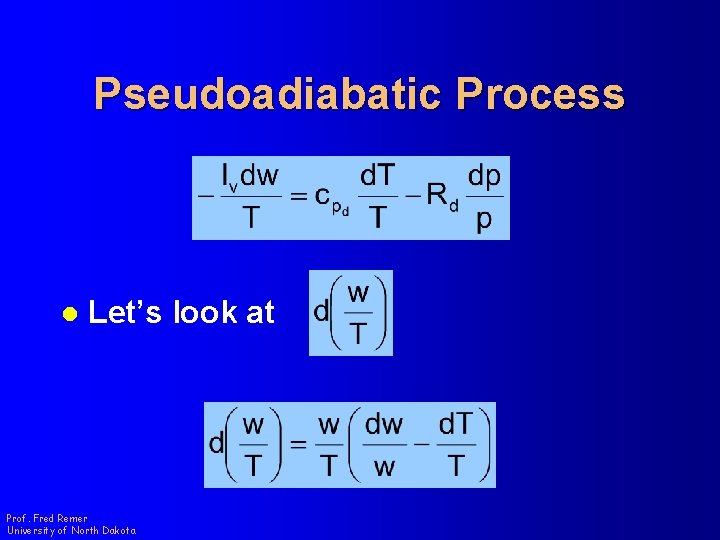
Pseudoadiabatic Process l Let’s look at Prof. Fred Remer University of North Dakota

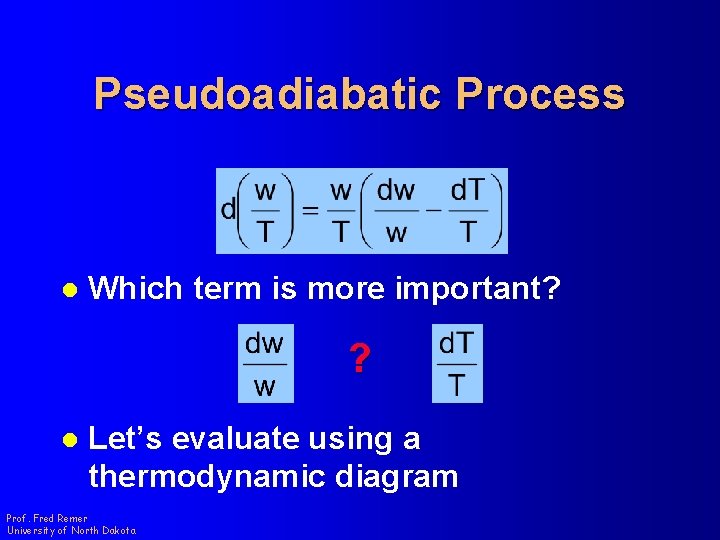
Pseudoadiabatic Process l Which term is more important? ? l Let’s evaluate using a thermodynamic diagram Prof. Fred Remer University of North Dakota

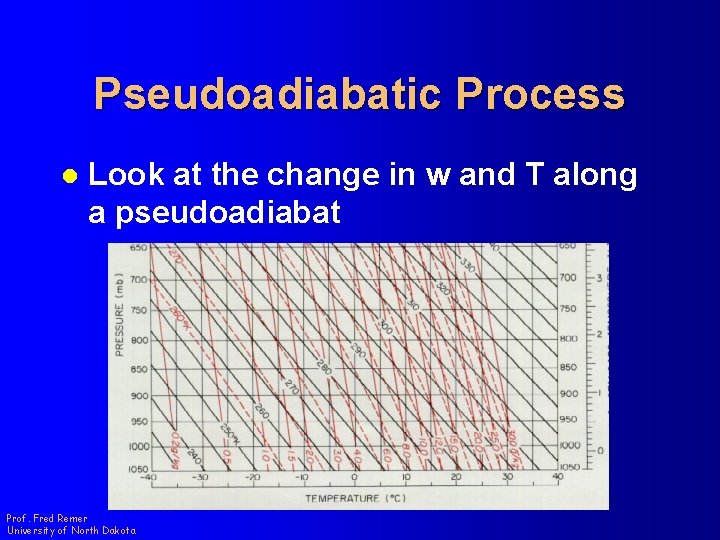
Pseudoadiabatic Process l Look at the change in w and T along a pseudoadiabat Prof. Fred Remer University of North Dakota

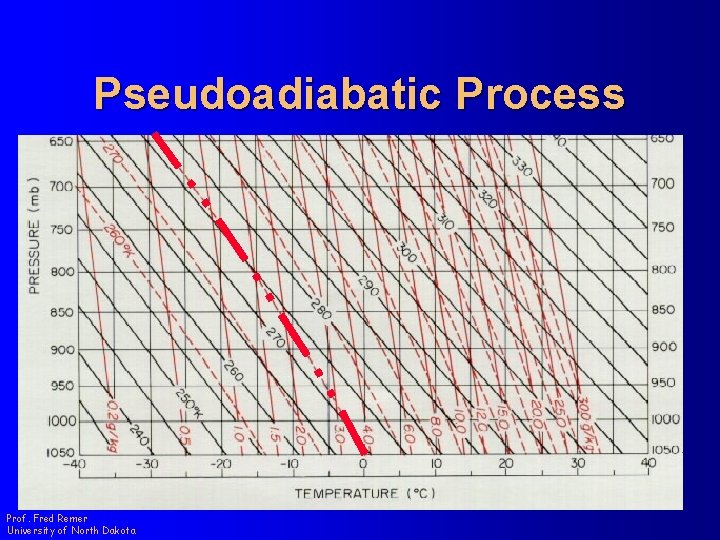
Pseudoadiabatic Process Prof. Fred Remer University of North Dakota

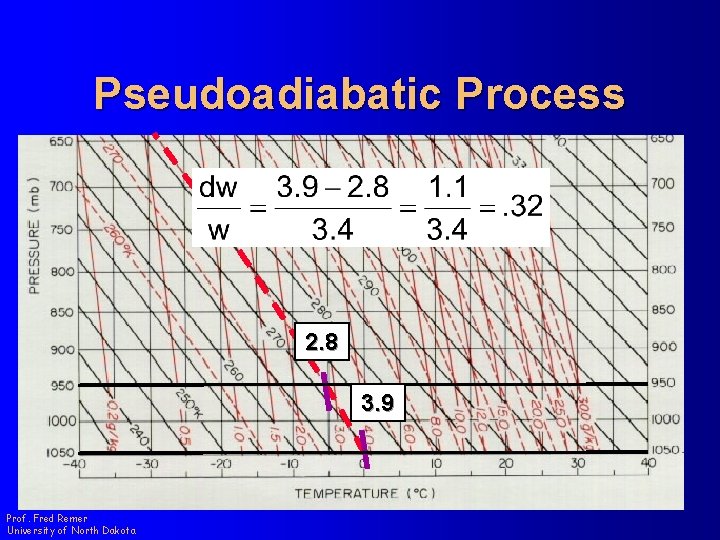
Pseudoadiabatic Process 2. 8 3. 9 Prof. Fred Remer University of North Dakota

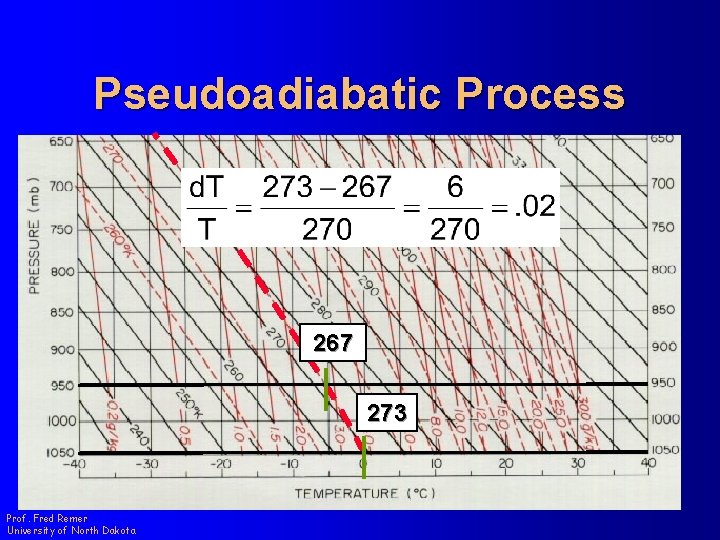
Pseudoadiabatic Process 267 273 Prof. Fred Remer University of North Dakota

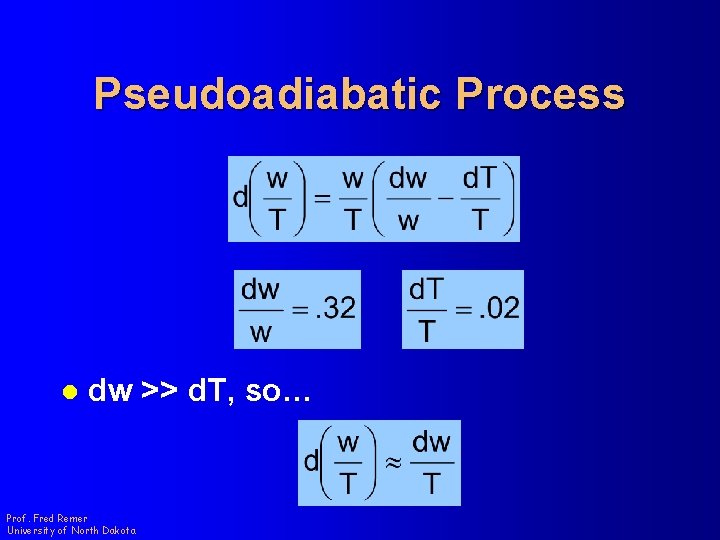
Pseudoadiabatic Process l dw >> d. T, so… Prof. Fred Remer University of North Dakota

Pseudoadiabatic Process l Plug back into the pseudoadiabatic equation Prof. Fred Remer University of North Dakota

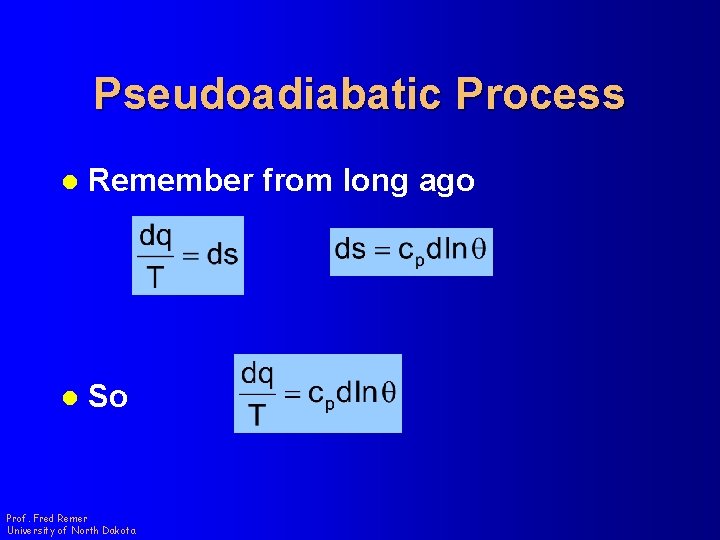
Pseudoadiabatic Process l Remember from long ago l So Prof. Fred Remer University of North Dakota

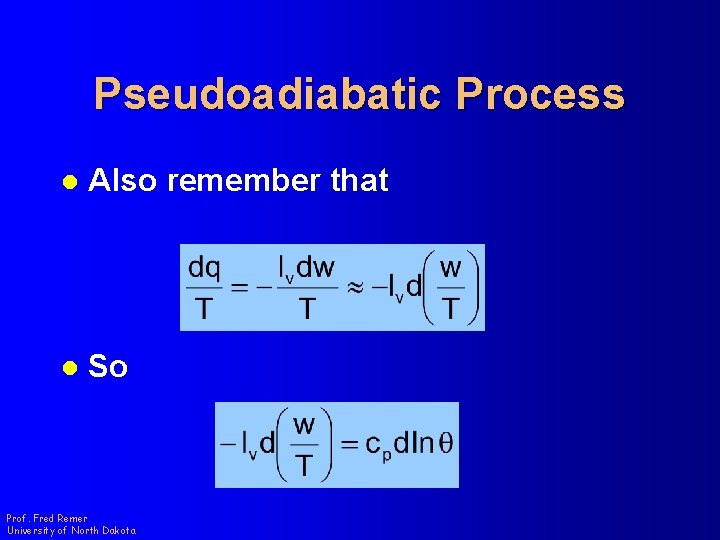
Pseudoadiabatic Process l Also remember that l So Prof. Fred Remer University of North Dakota

Pseudoadiabatic Process l Let’s integrate! ws = mixing ratio at q qe = potential temperature after all water vapor has condensed Prof. Fred Remer University of North Dakota

Pseudoadiabatic Process l Remember d. T is smaller than dw ws = mixing ratio at q qe = potential temperature after all water vapor has condensed Prof. Fred Remer University of North Dakota

Pseudoadiabatic Process l Integrate and evaluate the limits Prof. Fred Remer University of North Dakota

Pseudoadiabatic Process l Take the inverse natural logarithm Prof. Fred Remer University of North Dakota

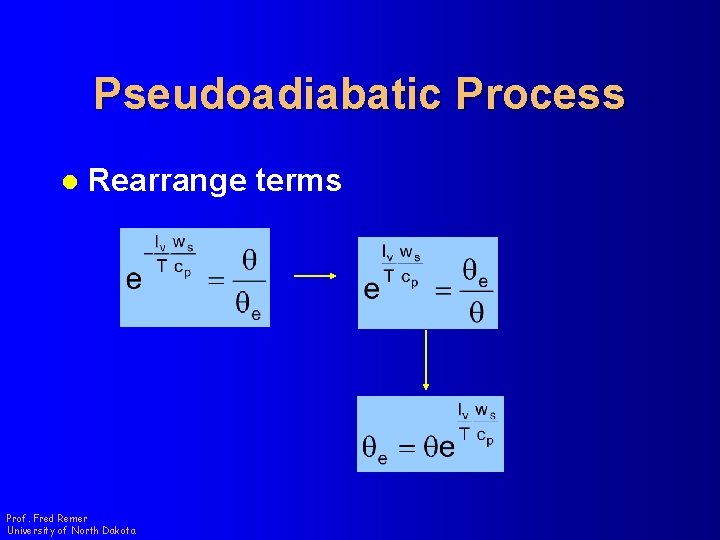
Pseudoadiabatic Process l Rearrange terms Prof. Fred Remer University of North Dakota

Equivalent Potential Temperature (qe ) l The potential temperature a parcel of air would have if all of its water vapor were condensed and the latent heat released warmed only the dry air. Prof. Fred Remer University of North Dakota

Equivalent Potential Temperature (qe ) ws = mixing ratio at once air has become saturated by adiabatic cooling or. . . mixing ratio at dew point Prof. Fred Remer University of North Dakota

Equivalent Potential Temperature (qe ) lv cp T q Prof. Fred Remer University of North Dakota = latent heat of vaporization = specific heat of dry air = temperature = potential temperature of air with temperature T and pressure p

Equivalent Potential Temperature (qe ) l A measure of the total energy of a parcel of air – Internal Energy – Energy from Latent Heat Prof. Fred Remer University of North Dakota

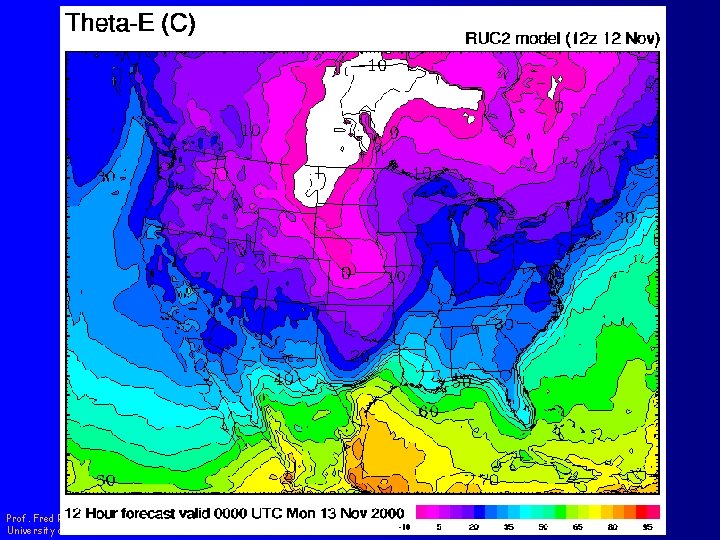
Equivalent Potential Temperature (qe ) Prof. Fred Remer University of North Dakota

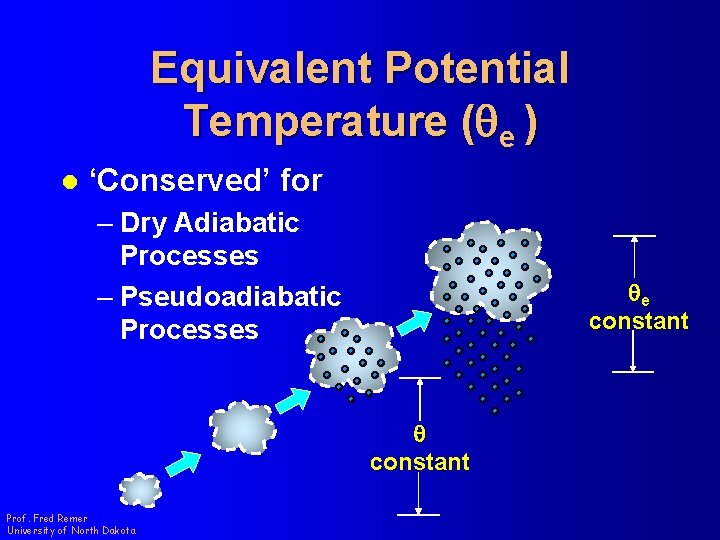
Equivalent Potential Temperature (qe ) l ‘Conserved’ for – Dry Adiabatic Processes – Pseudoadiabatic Processes qe constant q constant Prof. Fred Remer University of North Dakota

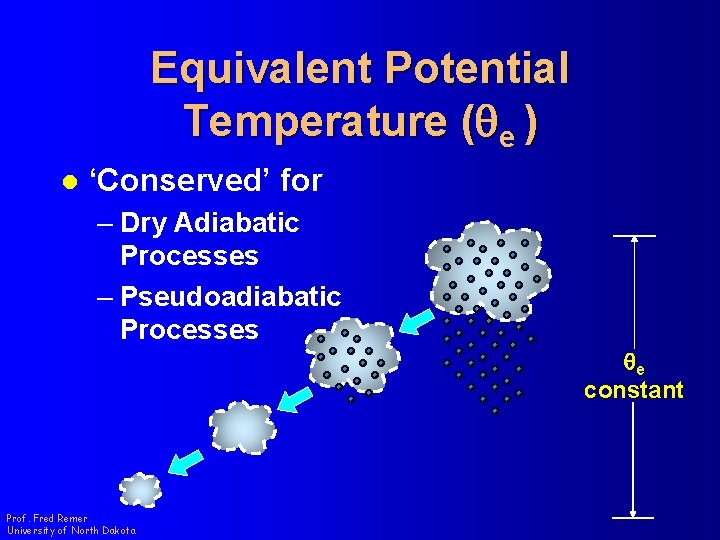
Equivalent Potential Temperature (qe ) l ‘Conserved’ for – Dry Adiabatic Processes – Pseudoadiabatic Processes Prof. Fred Remer University of North Dakota qe constant

Equivalent Potential Temperature (qe ) l As the air becomes drier (ws = 0), qe approaches q Prof. Fred Remer University of North Dakota

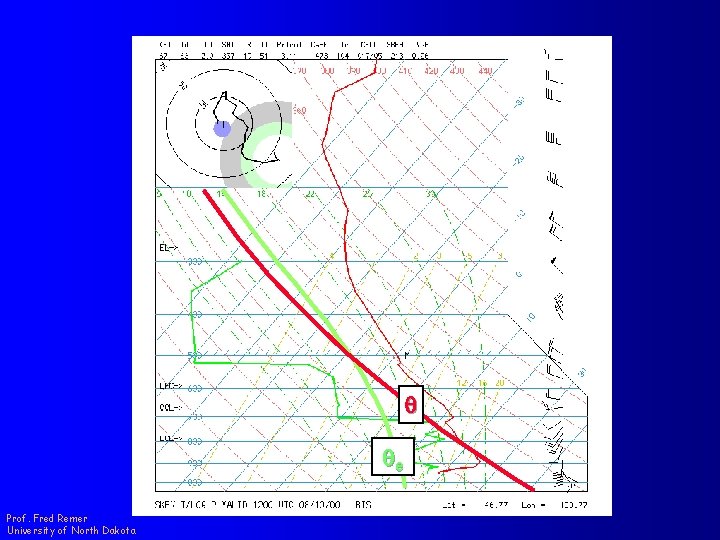
Equivalent Potential Temperature (qe ) q qe Prof. Fred Remer University of North Dakota

Review l Potential Temperature (q ) – The temperature a parcel of air would have if it were expanded or compressed adiabatically from its existing pressure and temperature to a standard pressure of 1000 mb. Prof. Fred Remer University of North Dakota

Review l Wet-Bulb Temperature (Tw) – The temperature to which air is cooled by evaporating water into it at constant pressure until the air is saturated Prof. Fred Remer University of North Dakota

Review l Wet Bulb Potential Temperature (qw ) – The wet bulb temperature the air would have if it were expanded or compressed adiabatically from its existing pressure and wet bulb temperature to a standard pressure of 1000 mb. Prof. Fred Remer University of North Dakota

Review l Virtual Temperature (Tv) – The temperature dry air must have in order to have the same density as moist air at the same pressure Prof. Fred Remer University of North Dakota

Review l Virtual Potential Temperature (qv ) – The virtual temperature the air would have if it were expanded or compressed adiabatically from its existing pressure and virtual temperature to a standard pressure of 1000 mb. Prof. Fred Remer University of North Dakota

Review l Equivalent Temperature (Te ) – The temperature a parcel of air would have if all of its water vapor were condensed and the latent heat released warmed only the dry air. Prof. Fred Remer University of North Dakota

Review l Equivalent Potential Temperature (qe ) – The potential temperature a parcel of air would have if all of its water vapor were condensed and the latent heat released warmed only the dry air. Prof. Fred Remer University of North Dakota

Prof. Fred Remer University of North Dakota