Modulo Graph Embedding Mapping Applications onto CoarseGrained Reconfigurable

Modulo Graph Embedding : Mapping Applications onto Coarse-Grained Reconfigurable Architectures Hyunchul Park, Kevin Fan, Manjunath Kudlur, Scott Mahlke Advanced Computer Architecture Lab University of Michigan 1 University of Michigan Electrical Engineering and Computer Science

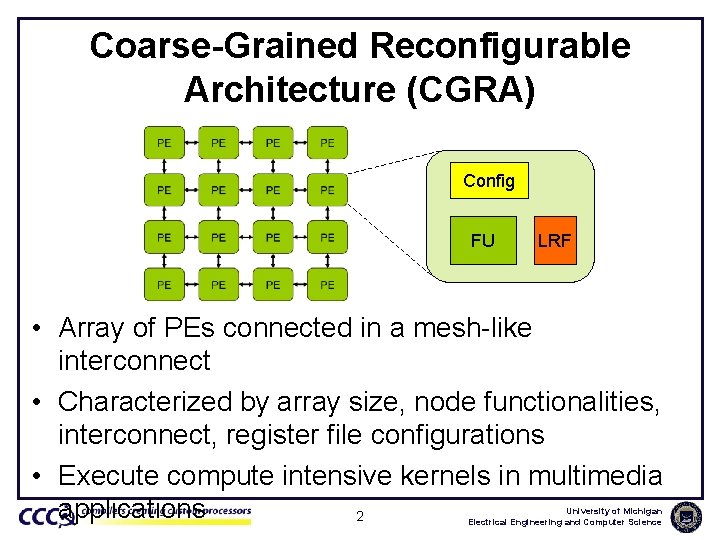
Coarse-Grained Reconfigurable Architecture (CGRA) Config FU LRF • Array of PEs connected in a mesh-like interconnect • Characterized by array size, node functionalities, interconnect, register file configurations • Execute compute intensive kernels in multimedia applications 2 University of Michigan Electrical Engineering and Computer Science

CGRA : Attractive Alternative to ASICs • Suitable for running multimedia applications on embedded systems – High computation throughput – Low power consumption and scalability – High flexibility with fast configuration • Morphosys : 8 x 8 array with RISC processor – SIMD style execution of loops • Piperench : 1 -D reconfigurable hardware – Virtualize hardware pipeline • ADRES : 8 x 8 array with tightly coupled VLIW – Modulo scheduling with simulated annealing 3 University of Michigan Electrical Engineering and Computer Science

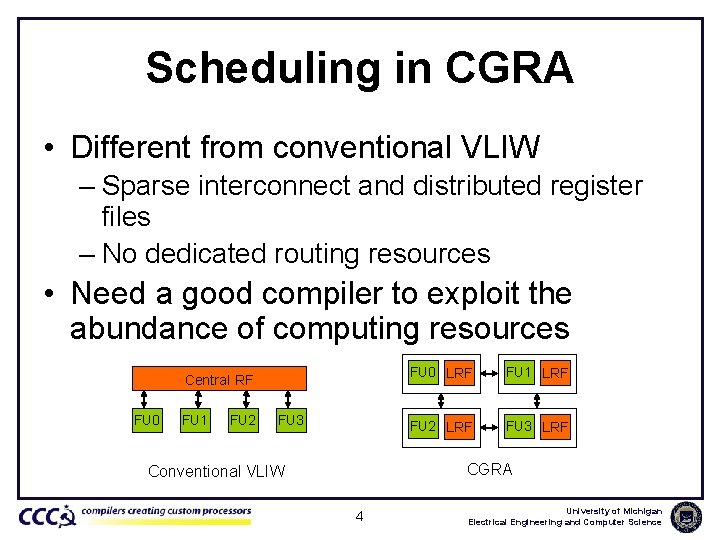
Scheduling in CGRA • Different from conventional VLIW – Sparse interconnect and distributed register files – No dedicated routing resources • Need a good compiler to exploit the abundance of computing resources Central RF FU 0 FU 1 FU 2 FU 3 FU 0 LRF FU 1 LRF FU 2 LRF FU 3 LRF CGRA Conventional VLIW 4 University of Michigan Electrical Engineering and Computer Science

Objectives of This Work • Modulo scheduling technique for CGRAs – Exploit loop-level parallelism by overlapping execution of iterations • Targeting low-cost CGRAs – Achieve quality schedule under restriction of hardware • Fast compilation time 5 University of Michigan Electrical Engineering and Computer Science

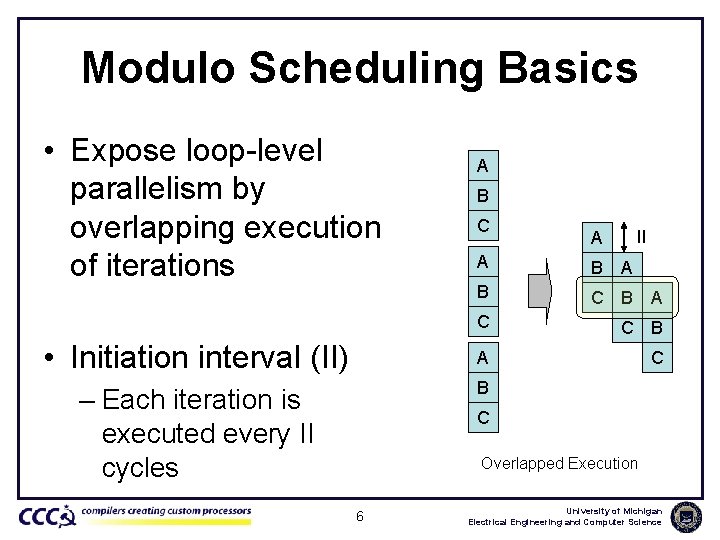
Modulo Scheduling Basics • Expose loop-level parallelism by overlapping execution of iterations A B C II A A B B C B A A C C B • Initiation interval (II) A C – Each iteration is executed every II cycles B C Overlapped Execution 6 University of Michigan Electrical Engineering and Computer Science

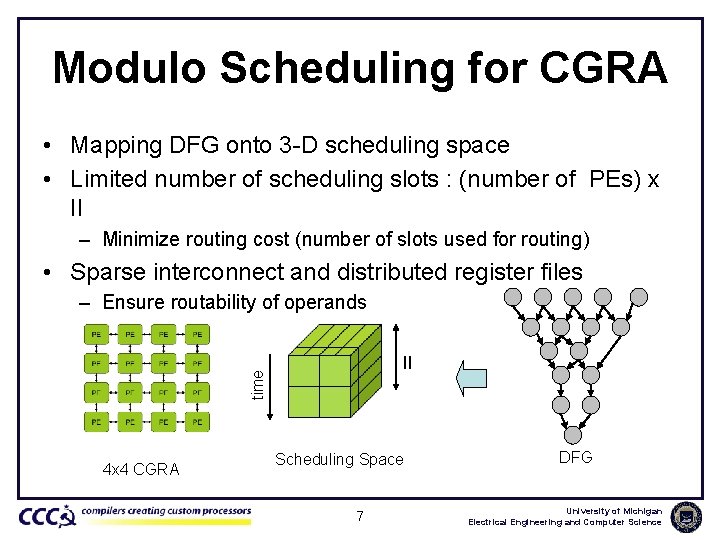
Modulo Scheduling for CGRA • Mapping DFG onto 3 -D scheduling space • Limited number of scheduling slots : (number of PEs) x II – Minimize routing cost (number of slots used for routing) • Sparse interconnect and distributed register files – Ensure routability of operands time II 4 x 4 CGRA Scheduling Space 7 DFG University of Michigan Electrical Engineering and Computer Science

Our Approach • Systematic approach to generate good schedule in reasonable time • Minimize routing cost – Convert scheduling problem into graph embedding – Leverage graph embedding algorithm • Ensure routability of operands – Skewed scheduling space – Create a narrow, but tall scheduling space 8 University of Michigan Electrical Engineering and Computer Science

1 : Minimize Routing Cost • Routing cost : number of PEs used for routing • Determined by positions of producer and consumer – Minimize distance between producers and consumers • Height-based list scheduling – Schedule operations in the order of dependence height – Place consumers close to producers 9 University of Michigan Electrical Engineering and Computer Science

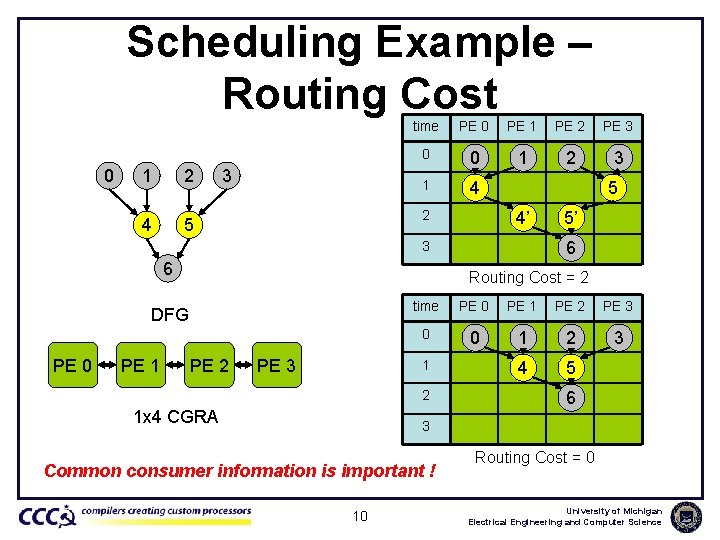
Scheduling Example – Routing Cost 0 1 2 4 5 3 time PE 0 PE 1 PE 2 PE 3 0 0 1 2 3 1 4 2 5 4’ 6 3 6 Routing Cost = 2 DFG PE 0 PE 1 5’ PE 2 PE 3 time PE 0 PE 1 PE 2 PE 3 0 0 1 2 3 4 5 1 2 1 x 4 CGRA 6 3 Common consumer information is important ! 10 Routing Cost = 0 University of Michigan Electrical Engineering and Computer Science

Affinity Graph Heuristic • Consider placement of operations with same height together – Use common consumer information • Affinity value between operations – Measured by the distance of common consumers in DFG • Construct affinity graph – Nodes : operations, edges : affinity values • Place operations with affinity edges close to each other 11 University of Michigan Electrical Engineering and Computer Science

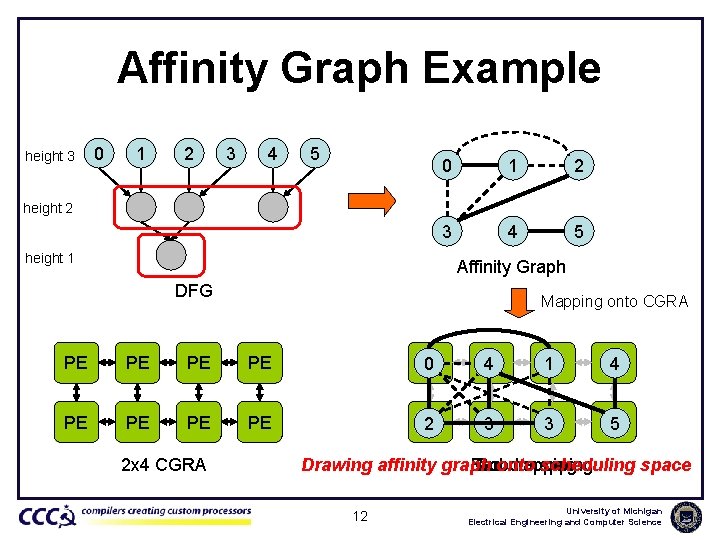
Affinity Graph Example height 3 0 1 2 3 4 5 height 2 height 1 Affinity Graph DFG Mapping onto CGRA PE PE 0 2 4 1 4 PE PE 1 2 3 3 5 2 x 4 CGRA Drawing affinity graph Bad Good onto mapping scheduling space 12 University of Michigan Electrical Engineering and Computer Science

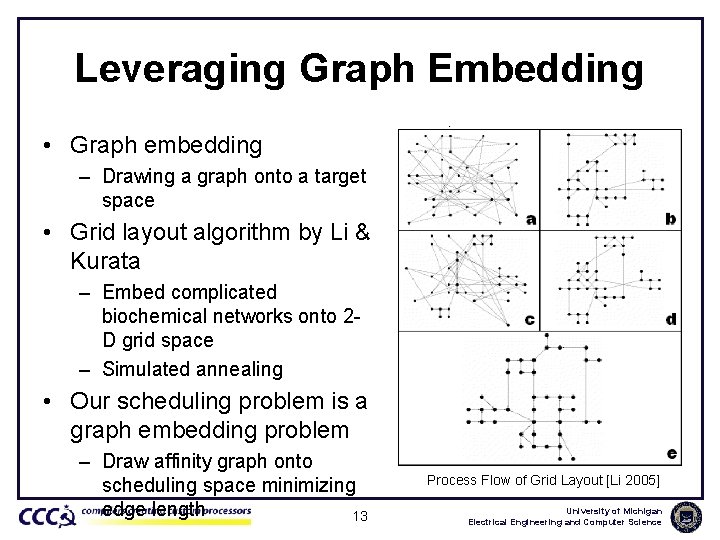
Leveraging Graph Embedding • Graph embedding – Drawing a graph onto a target space • Grid layout algorithm by Li & Kurata – Embed complicated biochemical networks onto 2 D grid space – Simulated annealing • Our scheduling problem is a graph embedding problem – Draw affinity graph onto scheduling space minimizing edge length 13 Process Flow of Grid Layout [Li 2005] University of Michigan Electrical Engineering and Computer Science

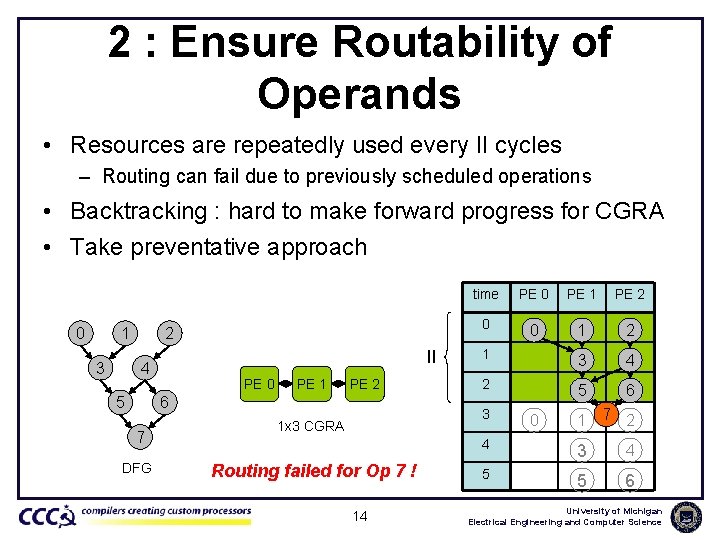
2 : Ensure Routability of Operands • Resources are repeatedly used every II cycles – Routing can fail due to previously scheduled operations • Backtracking : hard to make forward progress for CGRA • Take preventative approach 0 1 3 2 II 4 5 PE 0 PE 1 PE 2 6 7 DFG time PE 0 PE 1 PE 2 0 0 1 2 1 3 4 2 5 6 3 1 x 3 CGRA Routing failed for Op 7 ! 14 0 1 7 2 4 3 4 5 5 6 University of Michigan Electrical Engineering and Computer Science

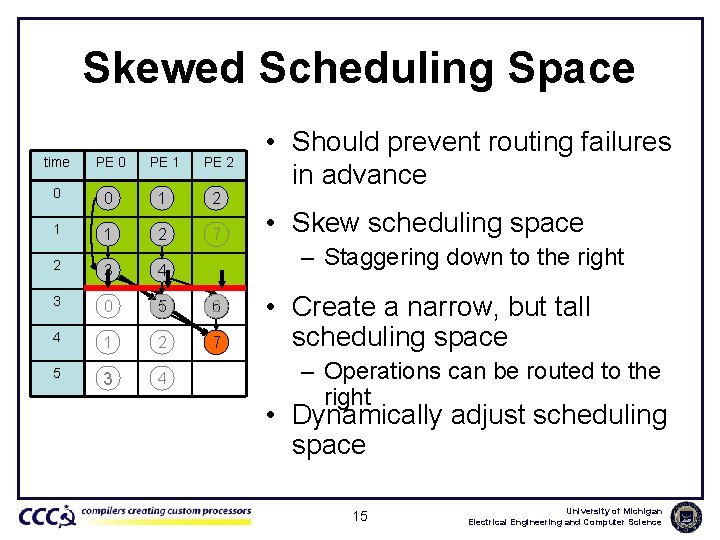
Skewed Scheduling Space time PE 0 PE 1 PE 2 0 0 1 5 2 6 1 1 2 7 2 3 4 3 0 1 5 2 6 4 1 2 7 5 3 4 • Should prevent routing failures in advance • Skew scheduling space – Staggering down to the right • Create a narrow, but tall scheduling space – Operations can be routed to the right • Dynamically adjust scheduling space 15 University of Michigan Electrical Engineering and Computer Science

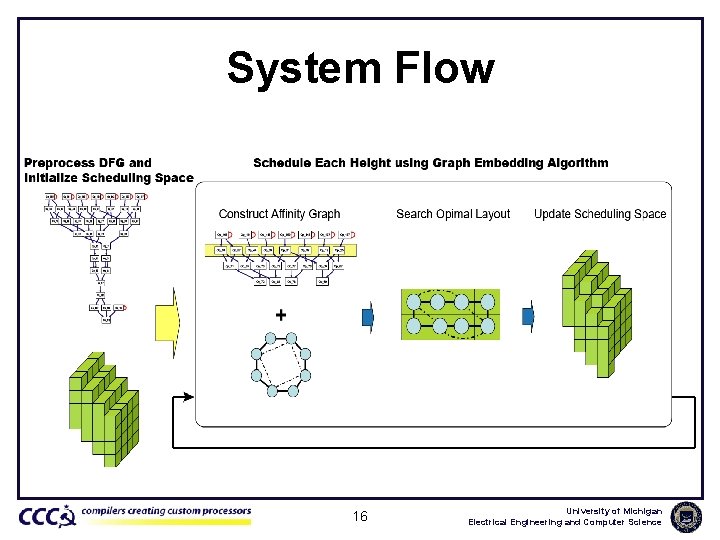
System Flow 16 University of Michigan Electrical Engineering and Computer Science

Experimental Setup • Twelve innermost loop kernels from various domains • Three designs with different RF configurations – Evaluate the impact of register file sharing Dedicated RF Shared RF Central RF 17 University of Michigan Electrical Engineering and Computer Science

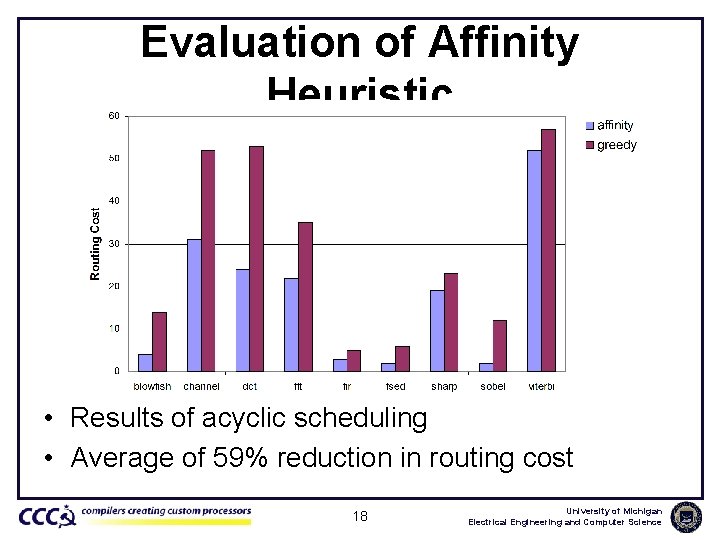
Evaluation of Affinity Heuristic • Results of acyclic scheduling • Average of 59% reduction in routing cost 18 University of Michigan Electrical Engineering and Computer Science

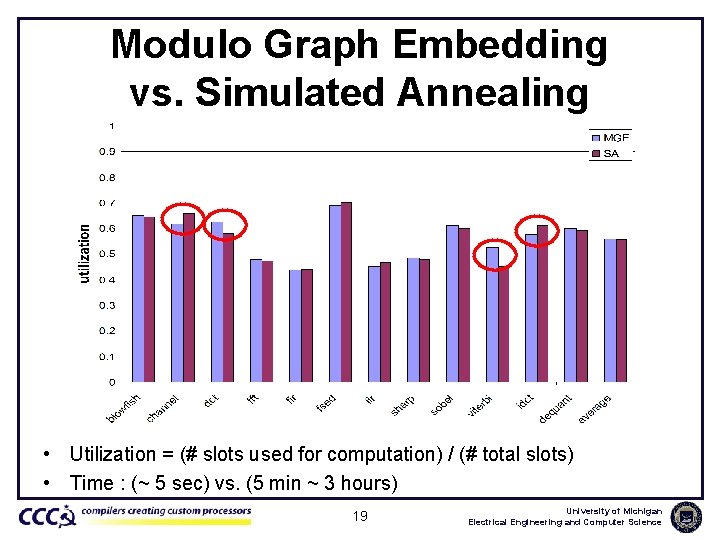
Modulo Graph Embedding vs. Simulated Annealing • Utilization = (# slots used for computation) / (# total slots) • Time : (~ 5 sec) vs. (5 min ~ 3 hours) 19 University of Michigan Electrical Engineering and Computer Science

Impact of Register File Configurations 20 University of Michigan Electrical Engineering and Computer Science

Conclusions • Modulo scheduler targeting low-cost CGRAs – Provide high computation throughput, scalability, power efficiency • Two heuristics to generate a good schedule – Affinity graph heuristic – Skewed scheduling space – Average utilizations of 56 -68% for three designs • Systematic approach 21 allows fast University of Michigan Electrical Engineering and Computer Science

Questions ? 22 University of Michigan Electrical Engineering and Computer Science