Module2 FFT Algorithms for N a Composite Number

Module-2 FFT Algorithms for N a Composite Number *Radix-2 FFT algorithm for the computation of DFT and *Radix-2 FFT algorithm for the computation of IDFT– *decimation-in-time and *decimation-in-frequency algorithms. *Goertzel algorithm, and *chirp-z transform.

Efficient computation of DFT : FFT Algorithms • Computationally efficient algorithms for evaluating DFT are described with two different approaches. i) Divide & conquer approach-in which a DFT of size N is reduced to the computation of smaller DFTs from which the larger DFT is computed. Ex: FFT algorithms, N is power of 2 ii) Formulation of DFT as a linear filtering operation on data. leads to two algorithms • Goertzel algorithm • Chirp Z-transform algorithm Ravi M. Hatti, Asst. Prof. , Dept of E&C, BLDEA’s CE&T, Vijayapur 2

Importance of DFT in various DSP applications • Ravi M. Hatti, Asst. Prof. , Dept of E&C, BLDEA’s CE&T, Vijayapur 3

• Ravi M. Hatti, Asst. Prof. , Dept of E&C, BLDEA’s CE&T, Vijayapur 4

Radix-2 FFT Algorithms • Ravi M. Hatti, Asst. Prof. , Dept of E&C, BLDEA’s CE&T, Vijayapur 5

• Ravi M. Hatti, Asst. Prof. , Dept of E&C, BLDEA’s CE&T, Vijayapur 6

• Ravi M. Hatti, Asst. Prof. , Dept of E&C, BLDEA’s CE&T, Vijayapur 7
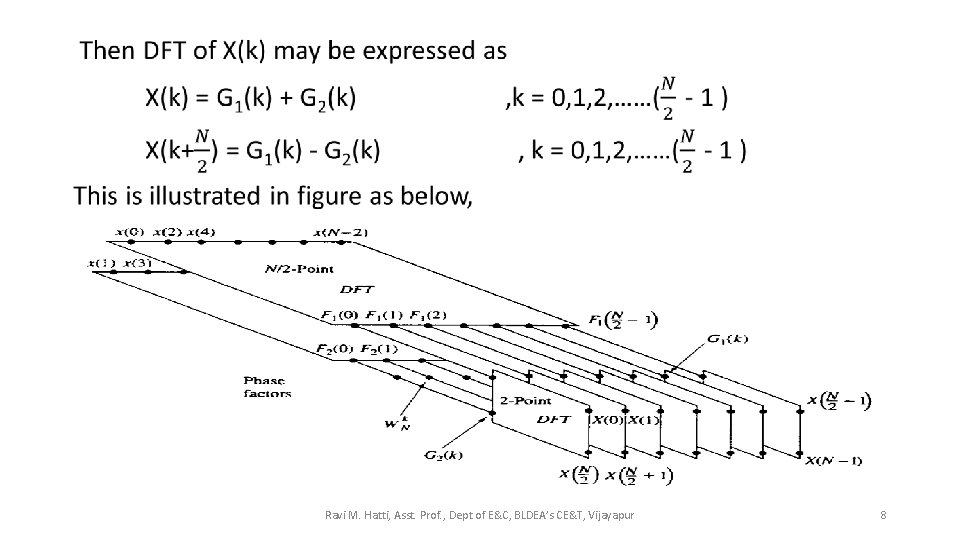
• Ravi M. Hatti, Asst. Prof. , Dept of E&C, BLDEA’s CE&T, Vijayapur 8

• Ravi M. Hatti, Asst. Prof. , Dept of E&C, BLDEA’s CE&T, Vijayapur 9

• Ravi M. Hatti, Asst. Prof. , Dept of E&C, BLDEA’s CE&T, Vijayapur 10
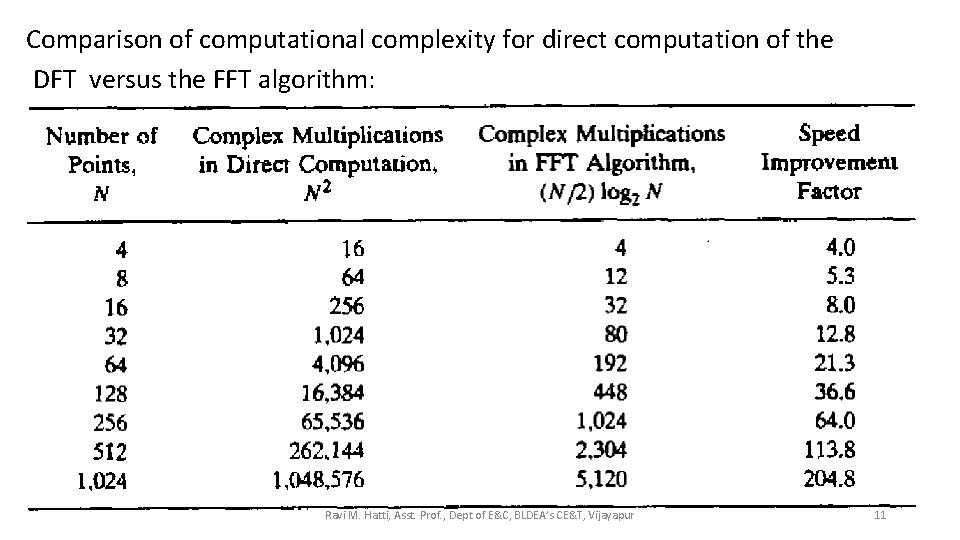
Comparison of computational complexity for direct computation of the DFT versus the FFT algorithm: Ravi M. Hatti, Asst. Prof. , Dept of E&C, BLDEA’s CE&T, Vijayapur 11
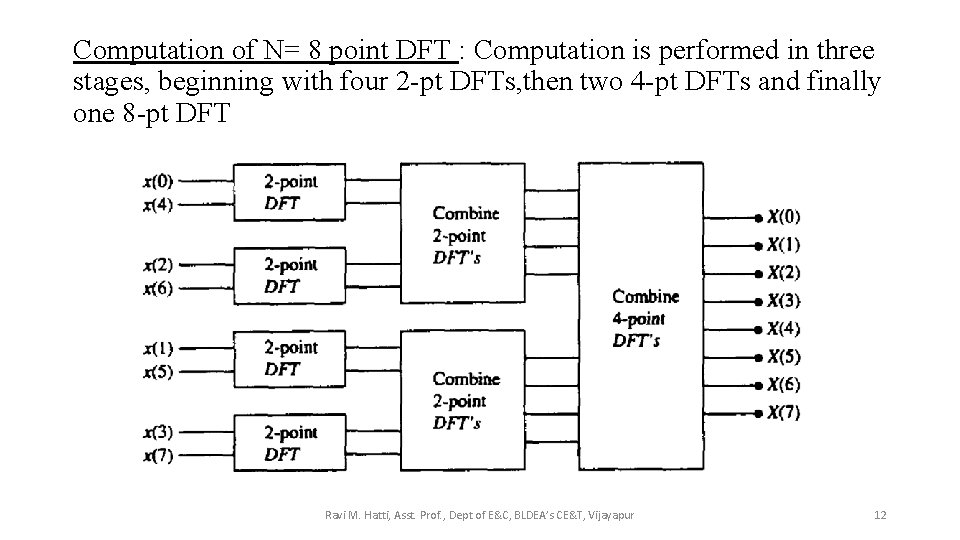
Computation of N= 8 point DFT : Computation is performed in three stages, beginning with four 2 -pt DFTs, then two 4 -pt DFTs and finally one 8 -pt DFT Ravi M. Hatti, Asst. Prof. , Dept of E&C, BLDEA’s CE&T, Vijayapur 12

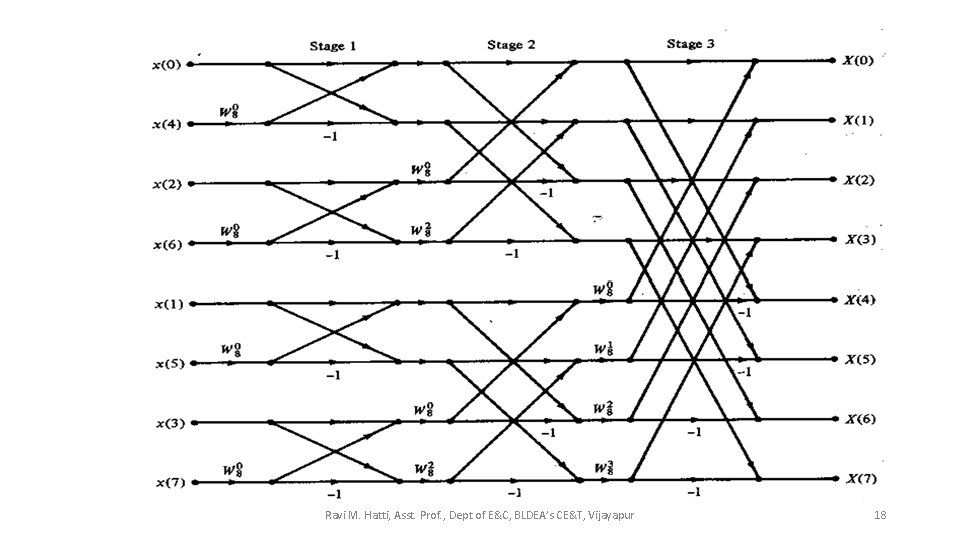
8 -pt DIT FFT algorithm : Combination of smaller DFTs to form larger DFTs (for N=8) Ravi M. Hatti, Asst. Prof. , Dept of E&C, BLDEA’s CE&T, Vijayapur 13

Basic Butterfly computation in DIT FFT algorithm • Ravi M. Hatti, Asst. Prof. , Dept of E&C, BLDEA’s CE&T, Vijayapur 14

Inplace computation: Once a butterfly operation is performed on a pair of complex numbers (a, b) to produce (A, B) , there is no need to save the input pair (a, b). Hence we store the result (A, B) in the same locations as (a, b). Hence we require a fixed amount of 2 N storage registers for each stage. Since same 2 N storage locations are used throughout the computation of N-pt DFT, it is said that the computations are done in-place. Order of input data sequence after it is decimated (v-1) times: For N=8, Ist decimation yields: x(0), x(2), x(4), x(6), x(1), x(3), x(5), x(7) IInd decimation yields: x(0), x(4), x(2), x(6), x(1), x(5), x(3), x(7) With input data sequence stored in bit-reversed order and butterfly operations done in-place, the resulting DFT sequence is obtained in natural order. Other way {input-natural order ; output-bit reversed} Ravi M. Hatti, Asst. Prof. , Dept of E&C, BLDEA’s CE&T, Vijayapur 15
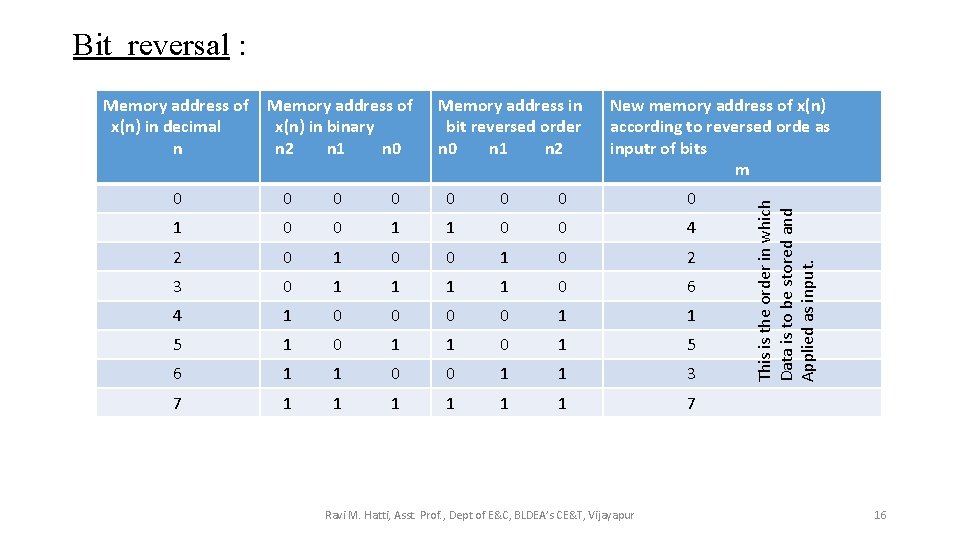
Bit reversal : Memory address of x(n) in binary n 2 n 1 n 0 Memory address in bit reversed order n 0 n 1 n 2 New memory address of x(n) according to reversed orde as inputr of bits m 0 0 0 0 1 1 0 0 4 2 0 1 0 2 3 0 1 1 0 6 4 1 0 0 1 1 5 1 0 1 5 6 1 1 0 0 1 1 3 7 1 1 1 7 Ravi M. Hatti, Asst. Prof. , Dept of E&C, BLDEA’s CE&T, Vijayapur This is the order in which Data is to be stored and Applied as input. Memory address of x(n) in decimal n 16

• Ravi M. Hatti, Asst. Prof. , Dept of E&C, BLDEA’s CE&T, Vijayapur 17
Ravi M. Hatti, Asst. Prof. , Dept of E&C, BLDEA’s CE&T, Vijayapur 18
- Slides: 18