MODULE V VOCABULARY PART I MODULE V This

MODULE V VOCABULARY PART I

MODULE V • This module is called “right triangles”. • We will be refining our study of triangles to only right triangles. • These have many special properties. • Many deal in some way with our old buddy Pythagoras.

MODULE V • Pythagoras was a Greek philosopher and mathematician. • He was actually so brilliant people began a religion in his honor called Pythagoreanism which basically worshipped the order and logic of math. • Even with that considered, he was sainted in 1929.

MODULE V • He gave us one of the most used and widely known theorems. • Then Pythagorean Theorem is used when dealing with the legs and hypotenuses of right triangles.

MODULE V • The Pythagorean theorem states that in a right triangle, the sum of the squares of the lengths of the legs is equal to the square of the length of the hypotenuse.

MODULE V • This is commonly written a² + b² = c² • a and b represent the legs and c represents the hypotenuse. • But this, we already know…

MODULE V • The way we would use theorem is as follows… • To find c in the picture below we square a and b, then take the square root of the result. c 3 4 • So since, 9 + 16 = 25…the length of c is 5.

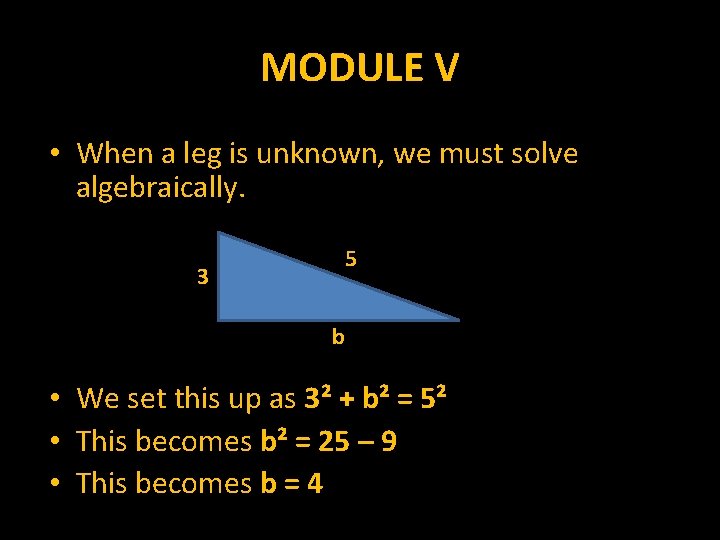
MODULE V • When a leg is unknown, we must solve algebraically. 3 5 b • We set this up as 3² + b² = 5² • This becomes b² = 25 – 9 • This becomes b = 4

MODULE V • What if our number to be square rooted is not a perfect square? c 4 7 • 16 + 49 = 65 so we would represent the length of c simply as √ 65

MODULE V • Finally, there are commonly used sets of numbers for called Pythagorean Triples. • The one you’ve seen in this presentation is 3, 4, 5. • Some others are… – 5, 12, 13 – 8, 15, 17 – 7, 24, 25 13 5 12

MODULE V • Any multiples of the Pythagorean triples will also work. • For instance, from the triple of 8, 15, 17 we could also make triangles of 16, 30, 34 and 24, 45, 51.

MODULE V • Sometimes you will be asked to solve triangles with Pythagorean triples. • For example, using Pythagorean triples, find x. x 30 40

MODULE V • Use Pythagorean triples to find x. 65 25 x

PYTHAGOREAN THEOREM • Finally, there are many real life examples of using the Pythagorean theorem. • One would be finding how high a ladder would reach on a wall.

MODULE V • Next time, we will be working with the angles of a triangle and how they play into these ratios.