Module U 08181 Computer Graphics graphics primitives part

Module U 08181: Computer Graphics • graphics primitives part 1: scan conversion and filling 1

Raster graphics • vector graphics systems draw lines -- will be discussed later • A raster (bitmapped) graphics display is a ‘grid’ of picture elements -- pixels, dots 2

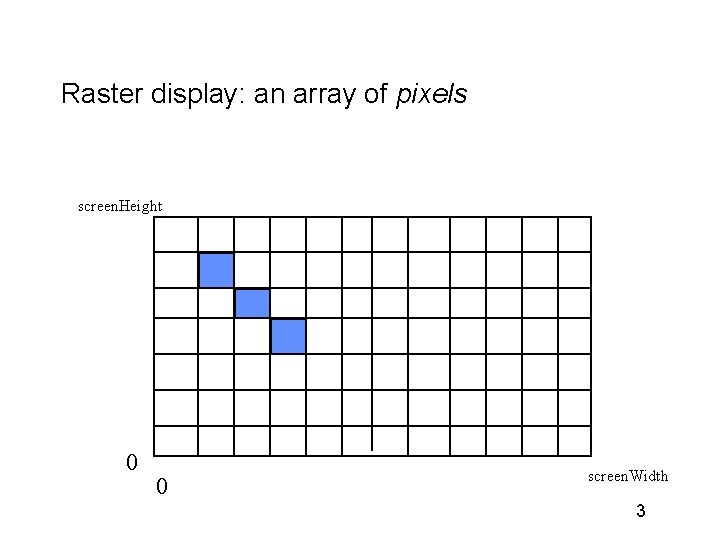
Raster display: an array of pixels screen. Height 0 0 screen. Width 3

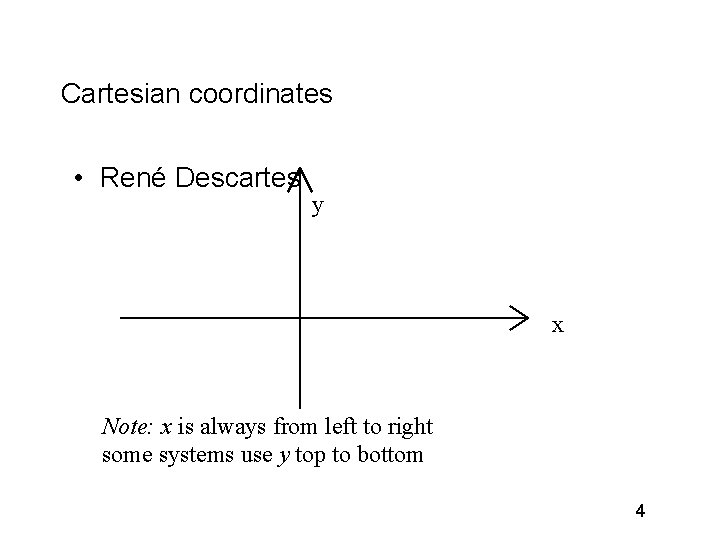
Cartesian coordinates • René Descartes y x Note: x is always from left to right some systems use y top to bottom 4

Scan conversion • cartesian coordinates: real, continuous • raster positions: integer, discrete • scan conversion: ‘rasterisation’, ‘discretisation’ 5

Raster access • PROCEDURE Set. Pixel (x, y: INTEGER; colour: INTEGER); (* pre: (x, y) is on screen post: pixel at (x, y) now in colour *) • FUNCTION Get. Pixel (x, y: INTEGER): INTEGER; (* pre: (x, y) is on screen post: Get. Pixel (x, y) is colour of pixel at (x, y) *) 6

How to set pixels to: • • draw lines draw curves: circles. . . display characters filled shapes 7

Simple lines • PROCEDURE Horizontal. Line (x, y, n: INTEGER); (* pre: all of line will lie on screen post: line of n units drawn from point (x, y) *) VAR i: INTEGER; BEGIN FOR i : = 0 TO n - 1 DO Set. Pixel(x+ i, y, black) END Horizontal. Line; 8

Other lines: arbitrary slope - naive approach PROCEDURE Line (x 1, y 1, x 2, y 2: INTEGER); VAR x, dy: INTEGER; y: REAL; BEGIN dx : = x 2 - x 1; dy : = y 2 - y 1; FOR x : = x 1 TO x 2 DO y : = (dy / dx) * (x - x 1) + y 1; Set. Pixel(x, ROUND(y), black) END Line; 9

Problems with naive approach: • uses real (float) arithmetic including division -slow • uses ROUND -- slow 10

Better method: Bresenham’s algorithm Jack Bresenham 11

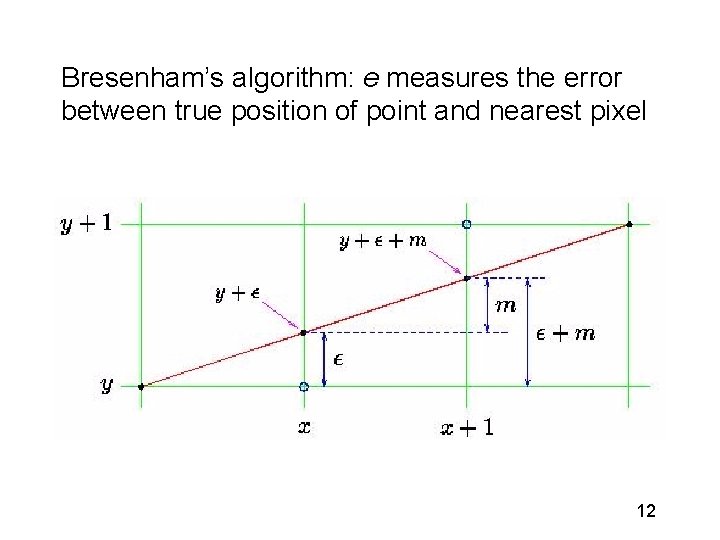
Bresenham’s algorithm: e measures the error between true position of point and nearest pixel 12

Bresenham’s algorithm: e measures the error between true position of point and nearest pixel simple version first: note precondition PROCEDURE Line (x 1, y 1, x 2, y 2: INTEGER); (* pre: dx > 0 & dy/dx < 1 post: line drawn from (x 1, y 1) to (x 2, y 2) *) VAR dx, dy, e, x, y: INTEGER; BEGIN dx : = x 2 - x 1; dy : = y 2 - y 1; y : = 0; e : = dx - 2*dy; 13

continued FOR x : = 0 TO dx DO Set. Pixel(x 1+ x, y 1 + y, black); IF e < 0 THEN y : = y + 1; e : = e + 2*(dx - dy) ELSE e : = e - 2*dy END END Line; 14

Advantages of Bresenham’s algorithm • uses only integer arithmetic - quick • multiplications only by 2 - quick, program as left shifts or leave to a (good) compiler to do this. • symmetry allows easy extension to slopes where dx > dy 15

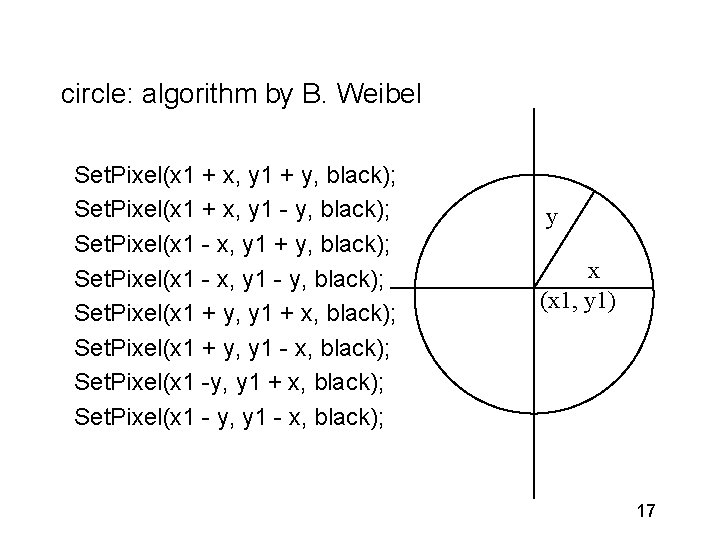
Circle: algorithm by B. Weibel • Note symmetry - we only need to draw one octant, then reflect, q is error measure PROCEDURE Circle (x 1, y 1, r: INTEGER); VAR x, y, q: INTEGER; BEGIN x : = 0; y : = r; q : = 4*r; WHILE x < y DO (* set current pixel in each octant *) 16

circle: algorithm by B. Weibel Set. Pixel(x 1 + x, y 1 + y, black); Set. Pixel(x 1 + x, y 1 - y, black); Set. Pixel(x 1 - x, y 1 + y, black); Set. Pixel(x 1 - x, y 1 - y, black); Set. Pixel(x 1 + y, y 1 + x, black); Set. Pixel(x 1 + y, y 1 - x, black); Set. Pixel(x 1 -y, y 1 + x, black); Set. Pixel(x 1 - y, y 1 - x, black); y x (x 1, y 1) 17

circle continued x : = x + 1; q : = q - (8*x - 4); IF q < 1 THEN y : = y - 1; q : = q + 8*y END; IF x = y THEN Set. Pixel(x 1 + x, y 1 + y, black); Set. Pixel(x 1 + x, y 1 - y, black); Set. Pixel(x 1 - x, y 1 + y, black); Set. Pixel(x 1 - x, y 1 - y, black); END Circle; 18

Other curves • More general curves can be obtained by: • B-spline • Bézier curves: developed for the UNISURF system by P. Bézier and used at Régie Renault for design of car bodies 19

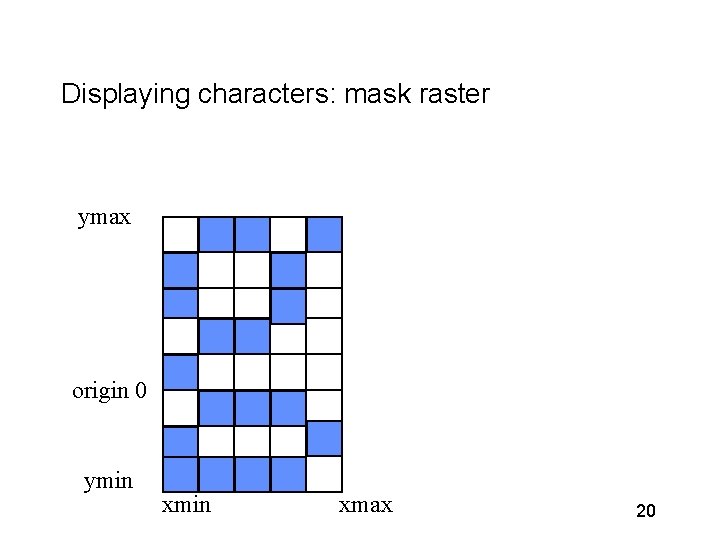
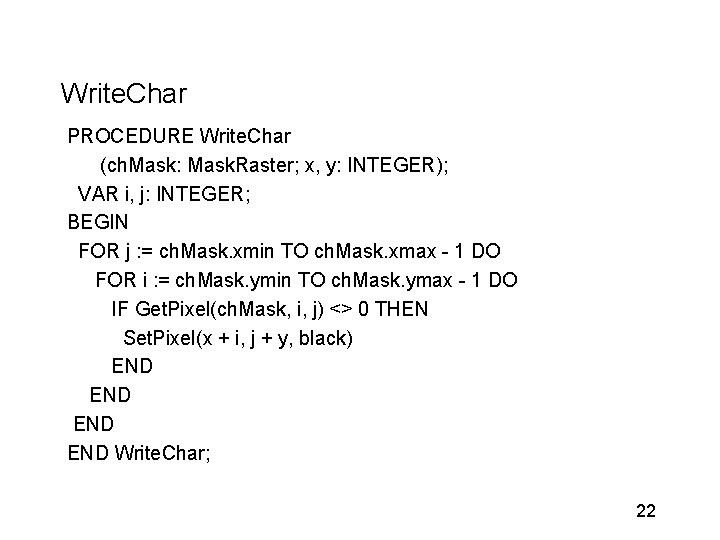
Displaying characters: mask raster ymax origin 0 ymin xmax 20

Italics and bold • Italics and bold can be created by algorithmic approach • Typographically unsophisticated 21

Write. Char PROCEDURE Write. Char (ch. Mask: Mask. Raster; x, y: INTEGER); VAR i, j: INTEGER; BEGIN FOR j : = ch. Mask. xmin TO ch. Mask. xmax - 1 DO FOR i : = ch. Mask. ymin TO ch. Mask. ymax - 1 DO IF Get. Pixel(ch. Mask, i, j) <> 0 THEN Set. Pixel(x + i, j + y, black) END END Write. Char; 22

Solid areas: Rectangle - easy PROCEDURE Filled. Rectangle (x, y, w, h: INTEGER); VAR i, j: INTEGER; BEGIN FOR j : = y TO y + h - 1 DO FOR i : = x TO x + w - 1 DO Set. Pixel(i, j, black) END END Filled. Rectangle; 23

‘Paintpot’ fill: Pick a point (x, y) within the shape, replace all pixels adjacent of old colour by new colour PROCEDURE Fill (x, y, old. Col, new. Col: INTEGER); VAR i, j: INTEGER; BEGIN IF Get. Pixel(x, y) = old. Col THEN Set. Pixel(x, y, new. Col); FOR i : = -1 TO 1 DO FOR j : = -1 TO 1 DO Fill(x + i, j + y, old. Col, new. Col) END END Fill; 24

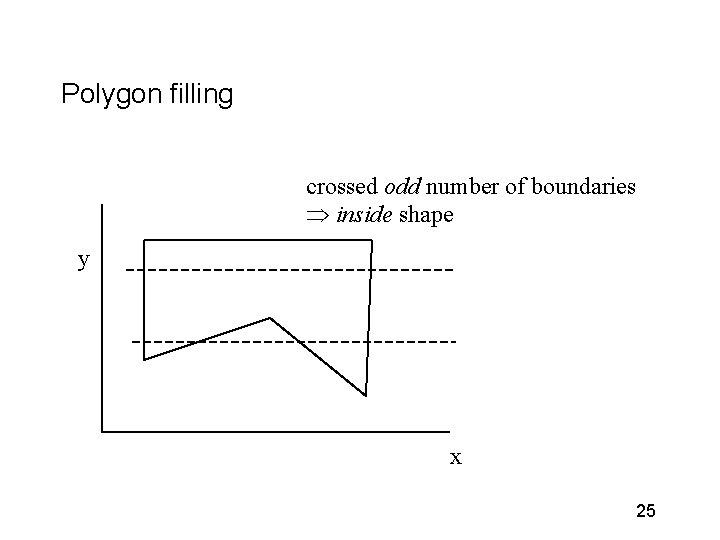
Polygon filling crossed odd number of boundaries Þ inside shape y x 25

Polygon filling • generate all the points (x, y) on periphery • sort points first by y, then by x • each pair of points(xa, y), (xb, y) is a region inside the polygon; • for each such pair fill pixels from (xa, y) to (xb, y) inclusive • can use dynamic data structure for this. 26

References • The original paper: Bresenham, J. E. : ‘Algorithm for Computer Control of a Digital Plotter, ’ IBM Sys. J. 4(1): 25 -30, 1965 • Bresenham’s home page: http: //www. udayton. edu/~cps/cps 560/notes/ Lines/bresnham. htm 27

References continued • An applet that demonstrates Bresenham’s algorithm (fun): http: //www. cs. rit. edu/~yxy 7691/Bookmark. htm l • Explanation and derivation: http: //www. cs. helsinki. fi/group/goa/mallinnus/li nes/bresenh. html • Explanation and derivation: http: //www. cs. unc. edu/~hoff/projects/comp 23 5/ 28 bresline/bresen. html

References continued • Circle algorithm: by B. Weibel, in ‘System Programming in Modula-2: Mouse and Bitmap Display’ (second edition) J. Gutknecht, Institut für Informatik, ETH Zürich, Sept 1983, p 44 • Bézier P. : ’Mathematical and Practical Possibilities of UNISURF’, in R. E. Barnhill and R. F. Riesenfeld (eds) Computer Aided Geometric Design, Academic, New York, 1974 29

Next lecture: clipping, transformations • Exercises – see separate exercise sheet 30