Module Programmation par contraintes 1 re anne Master

Module : Programmation par contraintes 1 ère année Master AD/Informatique Chapitre 2 : CSP binaire discret Dr. Sofiane Zaidi s. zaidi@univ-soukahras. dz 2019/2020 1

Contenu du cours (1/2) • CSP binaire • CSP discret • CSP continu • CSP binaire discret • Réseau de contraintes binaires • Binarisation • Relations associées à une contrainte ü Transposée d’une matrice ü Intersection de deux matrices booléennes ü Union de deux matrices booléennes ü Produit de deux matrices booléennes 2

Contenu du cours (2/2) • Représentation graphique d’un CSP binaire • Exemple d’un CSP binaire discret • Représentation graphique d’un CSP binaire • Représentation matricielle d’un CSP binaire • Sous-CSP d’un CSP binaire • Raffinement d’un CSP binaire 3

CSP binaire • Une contrainte est binaire si elle implique au plus deux variables. • Un CSP est binaire si toutes ses contraintes sont binaires. 4

CSP discret • Les domaines des variables sont finis, • Par exemple : ü Ensemble des couleurs = {Bleu, vert, rouge} ü Ensemble de personnes = {Mohamed, Ahmed, Amina, Abdellah} ü Ensemble des nombres = {0, 2, 3, 4, 6, 9} 5

CSP continu • Le domaine de chacune des variables est continu. • Par exemple, 6

CSP binaire discret • Toutes ses contraintes sont binaires et les domaines des variables sont finis. • Un CSP binaires discrets est défini par le triplet (X, D, C), tel que : ü X = {X 1 , …, Xn } sont les variables. ü D = {D(X 1 ), …, D(Xn )} sont les domaines des variables qui sont finis. ü C = {c 1 , …, cm} : sont des contraintes binaire 7

Réseau de contraintes binaires • Un réseau de contraintes est un ensemble de contraintes sur des variables ayant chacune un domaine fini et discret. • Un réseau de contraintes binaires peut être représenté par un graphe spécial : ü Les sommets représentent les variables. ü Les arêtes représentent les contraintes. Si les deux sommets sont adjacents, il y a une (des) contraintes sur ces variables. 8

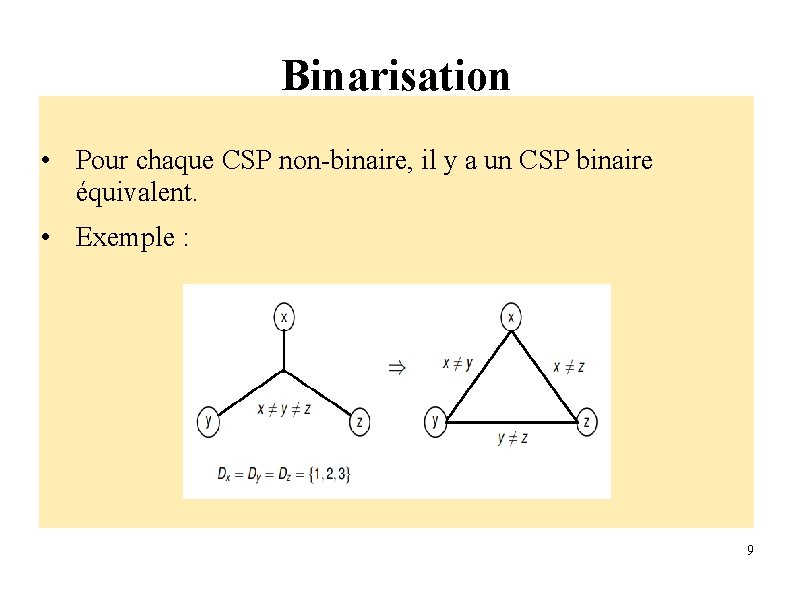
Binarisation • Pour chaque CSP non-binaire, il y a un CSP binaire équivalent. • Exemple : 9

Relations associées à une contrainte 10

Relations associées à une contrainte 11

Relations associées à une contrainte (Transposée d’une matrice) 12

Relations associées à une contrainte (Intersection de deux matrices booléennes) 13

Relations associées à une contrainte (Union de deux matrices booléennes) 14

Relations associées à une contrainte (Produit de deux matrices booléennes) 15

Représentation graphique d’un CSP binaire 16

Exemple d’un CSP binaire discret 17

Exemple d’un CSP binaire discret 18

Exemple d’un CSP binaire discret 19

Représentation graphique d’un CSP binaire 20

Représentation matricielle d’un CSP binaire 21

Sous-CSP d’un CSP binaire 22

Raffinement d’un CSP binaire 23