Module II Data Representation and Arithmetic Algorithms Integer

Negation of Integer • In sign-magnitude representation, negation is : invert the sign bit.

Case I : Consider Zero • There is carry out of MSB, which is

Case II • If we take the negation of the bit pattern of 1

Addition • Addition proceeds as if the two numbers were unsigned integers. • If

Addition • In some instances, there is a carry bit beyond the end of

Addition • On addition, the result may be larger than the word size used

Subtraction • To subtract one number (subtrahend) from another(minuend) take the 2’s complement of

Hardware for addition and subtraction • The binary adder is presented two numbers for

Hardware for addition and subtraction • For subtraction, the subtrahend (B register) is passed

START C, A 0 M Multiplicand Q Multiplier Count n No Yes Q 0

1101 X 1011 C A Q M Cnt 0 0000 1101 1011 4 START

START 1101 X 1011 C A 0 0000 Q M 1101 1011 C, A

START 1101 X 1011 C A Q M Cnt 0 0000 1101 1011 4

1101 X 1011 START C A Q M Cnt 0 0000 1101 1011 4

1101 X 1011 C A START Q M Cnt 0 0000 1101 1011 4

Problem Perform multiplication of numbers A =1001 and B=0011 using add-shift method.

Slides: 36

Download presentation

Module II Data Representation and Arithmetic Algorithms

Integer Arithmetic

Negation of Integer • In sign-magnitude representation, negation is : invert the sign bit. • In twos complement notation, negation is done with the following rules: 1. Take the Boolean complement of each bit of the integer (including the sign bit) 2. Treating the result as an unsigned binary integer, add 1. • This is referred to as twos complement operation.

Example

Two Special Cases

Case I : Consider Zero • There is carry out of MSB, which is ignored. • The result is that the negation of 0 is 0, as it should be.

Case II • If we take the negation of the bit pattern of 1 followed by n-1 zeros, we get back the same number. • In 2’s compliment, for n-bit length, there is a representation for – 2(n-1) but not for + 2(n-1)

Addition • Addition proceeds as if the two numbers were unsigned integers. • If the result of the operation is positive, we get a positive number in twos complement form • If the result of the operation is negative, we get a negative number in twos complement form.

Addition Example

Addition • In some instances, there is a carry bit beyond the end of the word, which is ignored.

Addition • On addition, the result may be larger than the word size used and it is called overflow • When overflow occurs, ALU must signal this fact before computation. • Rule to detect overflow: If two numbers are added, and they are both positive or both negative, then overflow occurs if and only if the result has the opposite sign.

Addition

Subtraction • To subtract one number (subtrahend) from another(minuend) take the 2’s complement of the subtrahend add it to minuend. • The overflow rule still applies.

Subtraction : Example

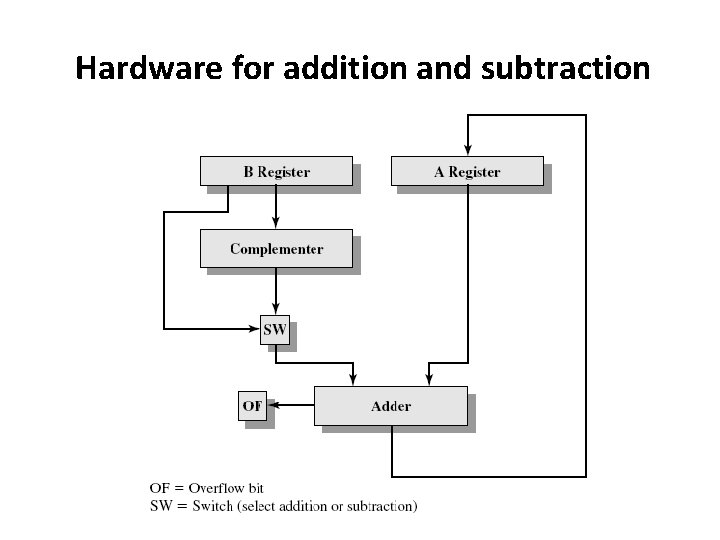
Hardware for addition and subtraction

Hardware for addition and subtraction • The binary adder is presented two numbers for addition and produces a sum and an overflow indication. • Adder treats two numbers as unsigned integers. • For addition, numbers are presented from two registers (A and B) and result is stored in A. • Overflow is indicated by 1 -bit overflow flag

Hardware for addition and subtraction • For subtraction, the subtrahend (B register) is passed through a twos complementer and then presented to the adder. • Control signals are needed to control whether or not the complementer is used, depending on whether addition or subtraction.

Multiplication

Unsigned Multiplication

Paper and Pencil Method

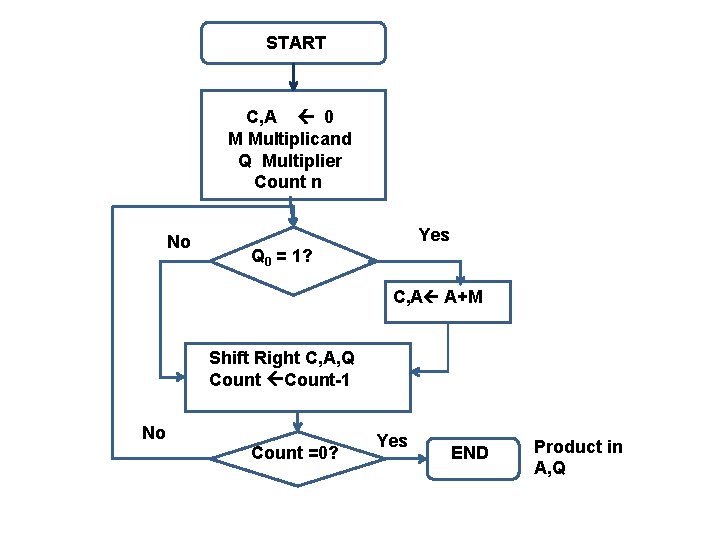
Computerized Unsigned Multiplication

START C, A 0 M Multiplicand Q Multiplier Count n No Yes Q 0 = 1? C, A A+M Shift Right C, A, Q Count-1 No Count =0? Yes END Product in A, Q

1101 X 1011 C A Q M Cnt 0 0000 1101 1011 4 START C, A 0 M Multiplicand Q Multiplier Count n Initial values No Yes Q 0 = 1? C, A A+M Shift Right C, A, Q Count-1 No Count =0? Yes END Product in A, Q

START 1101 X 1011 C A 0 0000 Q M 1101 1011 C, A 0 M Multiplicand Q Multiplier Count n Cnt 4 Initial values N o Yes Q 0 = 1? C, A A+M Shift Right C, A, Q Count-1 Yes Count =0? N o END Produc t in A, Q

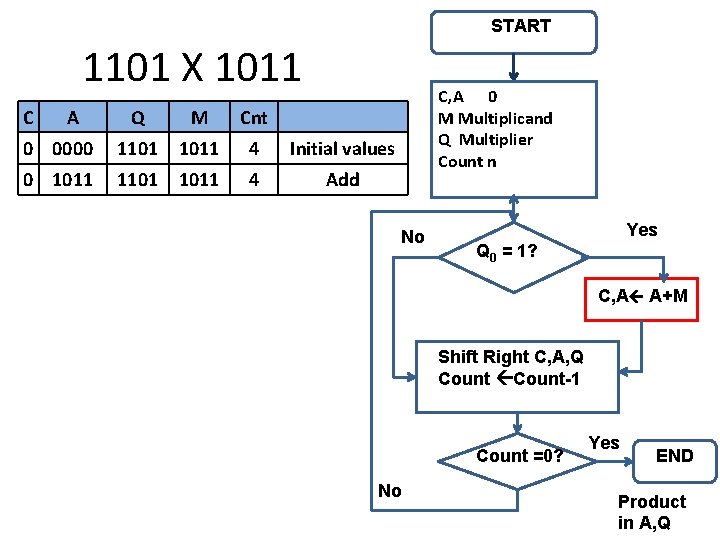
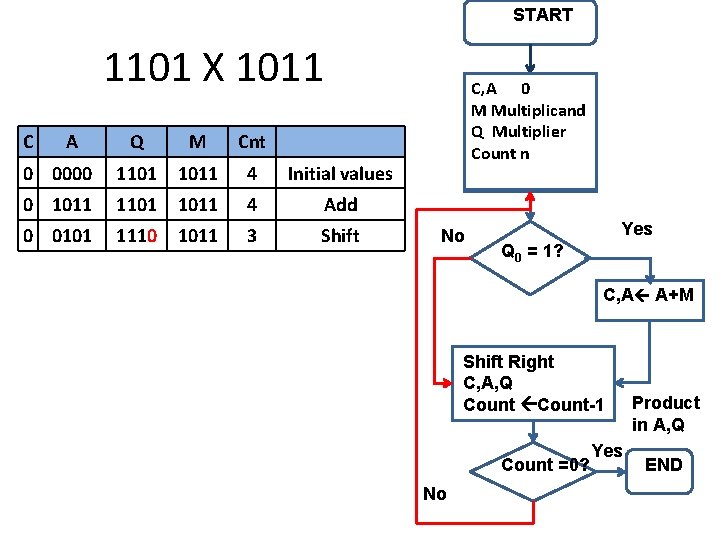
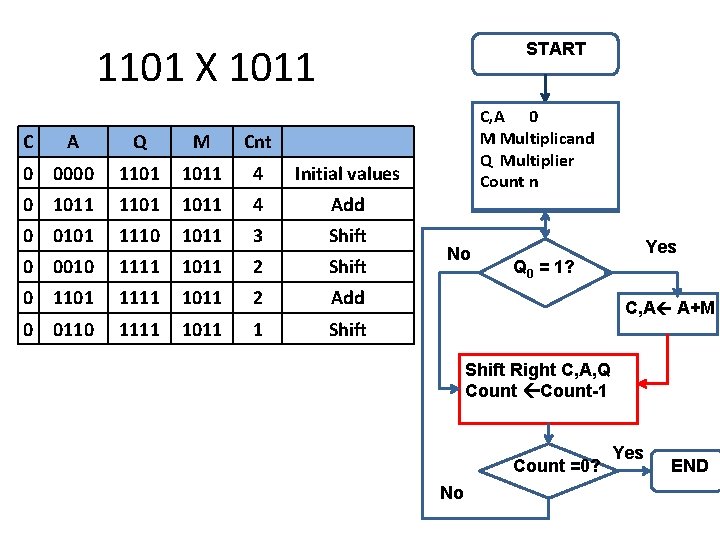
START 1101 X 1011 C A Q M Cnt 0 0000 1101 1011 4 Initial values 0 1011 1101 1011 4 Add C, A 0 M Multiplicand Q Multiplier Count n No Yes Q 0 = 1? C, A A+M Shift Right C, A, Q Count-1 Count =0? No Yes END Product in A, Q

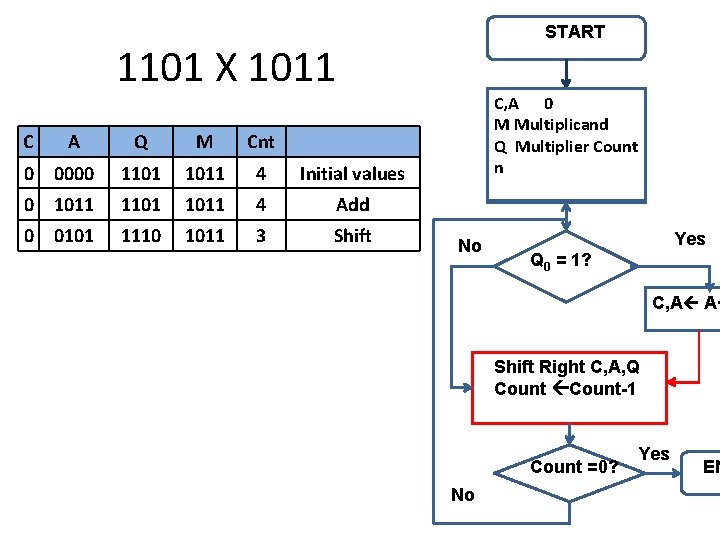
START 1101 X 1011 C A Q M Cnt 0 0000 1101 1011 4 Initial values 0 1011 1101 1011 4 Add 0 0101 1110 1011 3 Shift C, A 0 M Multiplicand Q Multiplier Count n No Yes Q 0 = 1? C, A A+ Shift Right C, A, Q Count-1 Count =0? No Yes EN

START 1101 X 1011 C A Q M Cnt 0 0000 1101 1011 4 Initial values 0 1011 1101 1011 4 Add 0 0101 1110 1011 3 Shift C, A 0 M Multiplicand Q Multiplier Count n No Yes Q 0 = 1? C, A A+M Shift Right C, A, Q Count-1 Count =0? No Yes Product in A, Q END

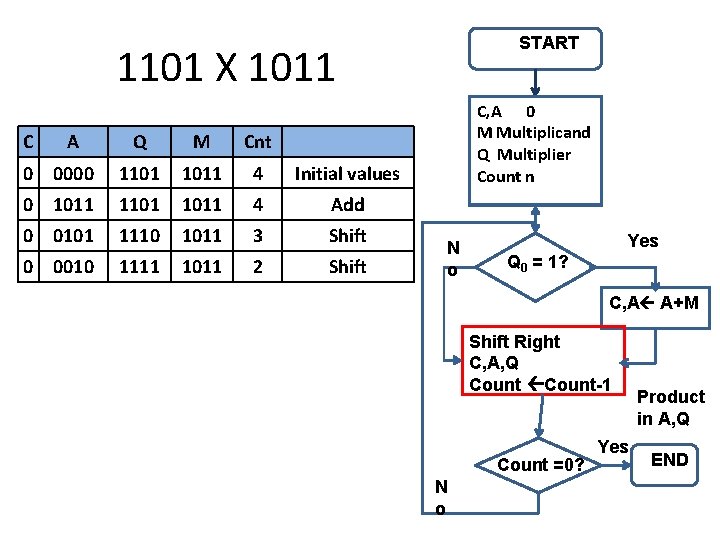
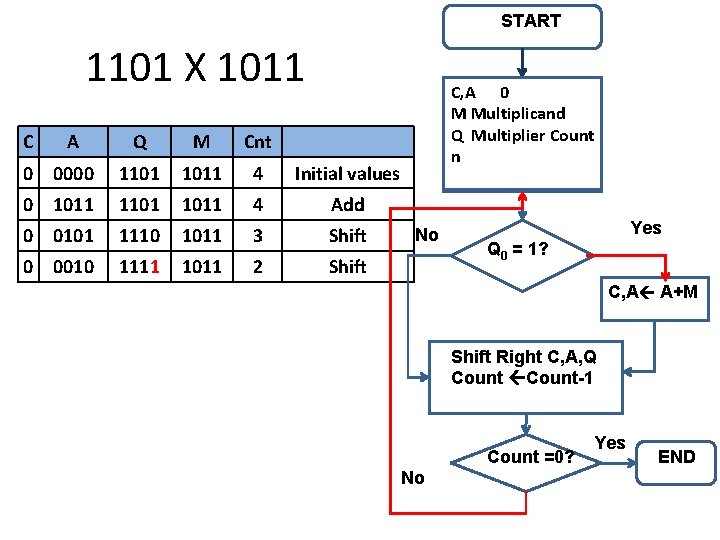
START 1101 X 1011 C A Q M Cnt 0 0000 1101 1011 4 Initial values 0 1011 1101 1011 4 Add 0 0101 1110 1011 3 Shift 0 0010 1111 1011 2 Shift C, A 0 M Multiplicand Q Multiplier Count n N o Yes Q 0 = 1? C, A A+M Shift Right C, A, Q Count-1 Count =0? N o Yes Product in A, Q END

START 1101 X 1011 C A Q M Cnt 0 0000 1101 1011 4 Initial values 0 1011 1101 1011 4 Add 0 0101 1110 1011 3 Shift 0 0010 1111 1011 2 Shift C, A 0 M Multiplicand Q Multiplier Count n No Yes Q 0 = 1? C, A A+M Shift Right C, A, Q Count-1 Count =0? No Yes END

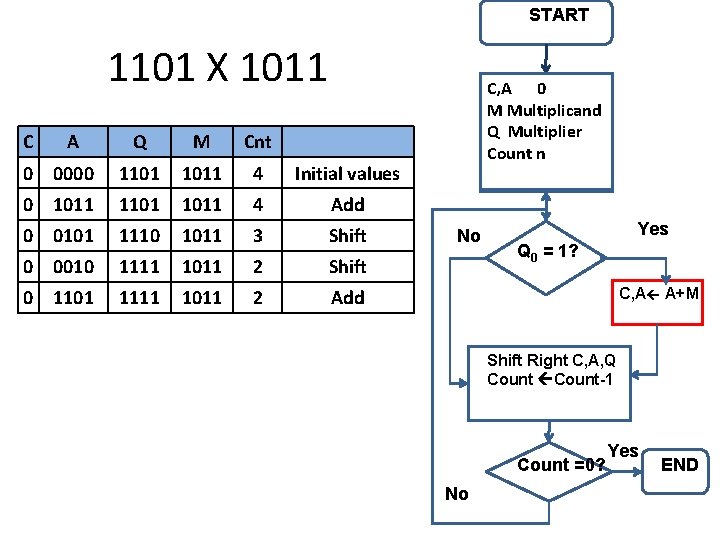
START 1101 X 1011 C A Q M Cnt 0 0000 1101 1011 4 Initial values 0 1011 1101 1011 4 Add 0 0101 1110 1011 3 Shift 0 0010 1111 1011 2 Shift 0 1101 1111 1011 2 Add C, A 0 M Multiplicand Q Multiplier Count n No Yes Q 0 = 1? C, A A+M Shift Right C, A, Q Count-1 Count =0? No Yes END

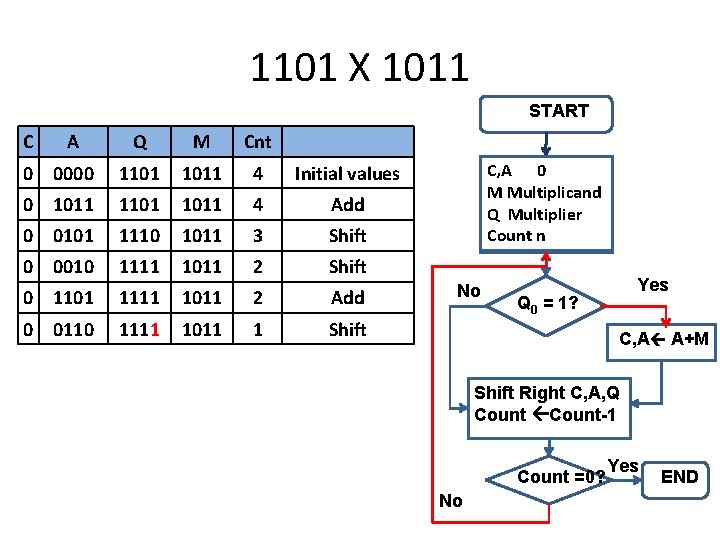
START 1101 X 1011 C A Q M Cnt 0 0000 1101 1011 4 Initial values 0 1011 1101 1011 4 Add 0 0101 1110 1011 3 Shift 0 0010 1111 1011 2 Shift 0 1101 1111 1011 2 Add 0 0110 1111 1011 1 Shift C, A 0 M Multiplicand Q Multiplier Count n No Yes Q 0 = 1? C, A A+M Shift Right C, A, Q Count-1 Count =0? No Yes END

1101 X 1011 START C A Q M Cnt 0 0000 1101 1011 4 Initial values 0 1011 1101 1011 4 Add 0 0101 1110 1011 3 Shift 0 0010 1111 1011 2 Shift 0 1101 1111 1011 2 Add 0 0110 1111 1011 1 Shift C, A 0 M Multiplicand Q Multiplier Count n No Yes Q 0 = 1? C, A A+M Shift Right C, A, Q Count-1 Count =0? No Yes END

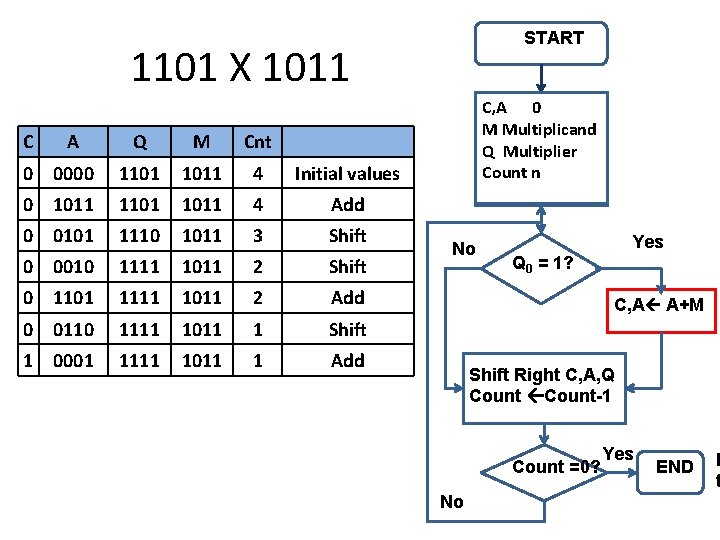
START 1101 X 1011 C A Q M Cnt 0 0000 1101 1011 4 Initial values 0 1011 1101 1011 4 Add 0 0101 1110 1011 3 Shift 0 0010 1111 1011 2 Shift 0 1101 1111 1011 2 Add 0 0110 1111 1011 1 Shift 1 0001 1111 1011 1 Add C, A 0 M Multiplicand Q Multiplier Count n No Yes Q 0 = 1? C, A A+M Shift Right C, A, Q Count-1 Count =0? No Yes END P t

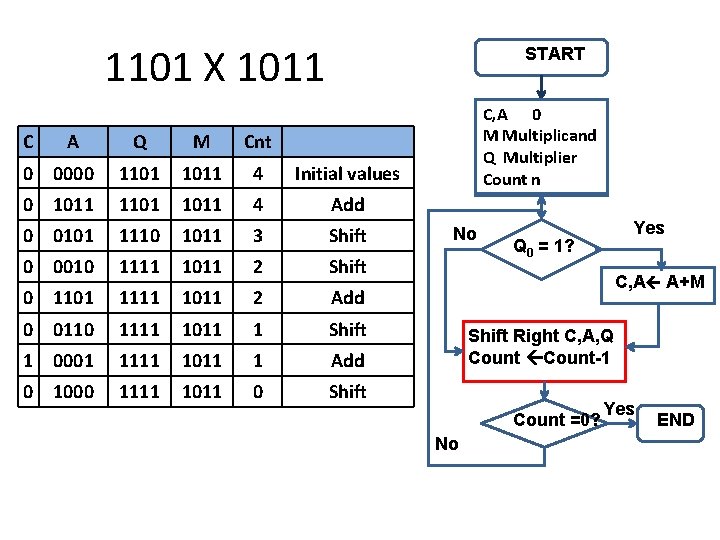
1101 X 1011 C A START Q M Cnt 0 0000 1101 1011 4 Initial values 0 1011 1101 1011 4 Add 0 0101 1110 1011 3 Shift 0 0010 1111 1011 2 Shift 0 1101 1111 1011 2 Add 0 0110 1111 1011 1 Shift 1 0001 1111 1011 1 Add 0 1000 1111 1011 0 Shift C, A 0 M Multiplicand Q Multiplier Count n No Yes Q 0 = 1? C, A A+M Shift Right C, A, Q Count-1 Count =0? No Yes END

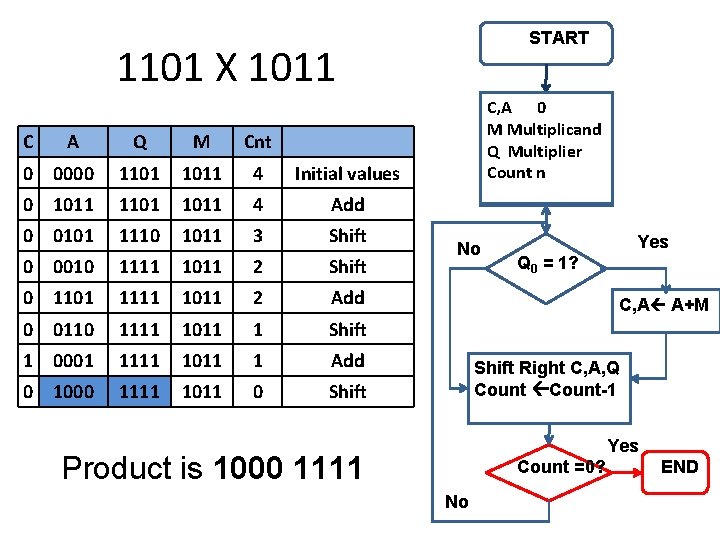
START 1101 X 1011 C A Q M Cnt 0 0000 1101 1011 4 Initial values 0 1011 1101 1011 4 Add 0 0101 1110 1011 3 Shift 0 0010 1111 1011 2 Shift 0 1101 1111 1011 2 Add 0 0110 1111 1011 1 Shift 1 0001 1111 1011 1 Add 0 1000 1111 1011 0 Shift C, A 0 M Multiplicand Q Multiplier Count n No Yes Q 0 = 1? C, A A+M Shift Right C, A, Q Count-1 Yes Product is 1000 1111 Count =0? No END

Problem Perform multiplication of numbers A =1001 and B=0011 using add-shift method.