MODULE A DECISIONMAKING TOOLS OUTLINE THE DECISION PROCESS

MODULE A DECISION-MAKING TOOLS

OUTLINE • THE DECISION PROCESS IN OPERATIONS • FUNDAMENTALS OF DECISION MAKING • DECISION TABLES • TYPES OF DECISION-MAKING ENVIRONMENTS • DECISION TREES

LEARNING OBJECTIVES WHEN YOU COMPLETE THIS CHAPTER YOU SHOULD BE ABLE TO: 1. Create a simple decision tree 2. Build a decision table 3. Explain when to use each of the three types of decisionmaking environments 4. Calculate an expected monetary value (EMV)

LEARNING OBJECTIVES WHEN YOU COMPLETE THIS CHAPTER YOU SHOULD BE ABLE TO: 5. Compute the expected value of perfect information (EVPI) 6. Evaluate the nodes in a decision tree 7. Create a decision tree with sequential decisions

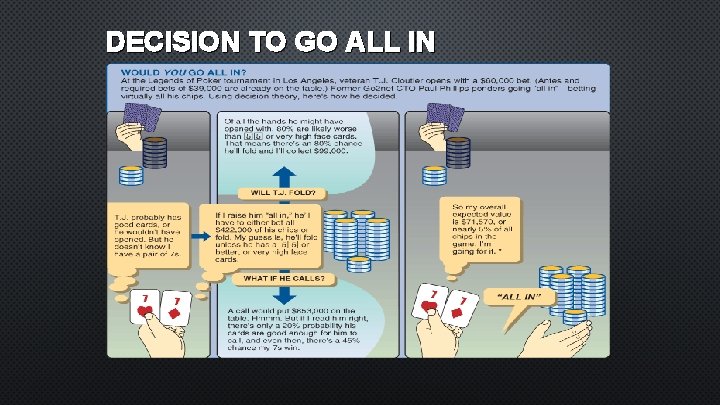
DECISION TO GO ALL IN

THE DECISION PROCESS IN OPERATIONS 1. Clearly define the problem and the factors that influence it 2. Develop specific and measurable objectives 3. Develop a model 4. Evaluate each alternative solution 5. Select the best alternative 6. Implement the decision and set a timetable for completion

FUNDAMENTALS OF DECISION MAKING 1. Terms: a. Alternative – a course of action or strategy that may be chosen by the decision maker b. State of nature – an occurrence or a situation over which the decision maker has little or no control

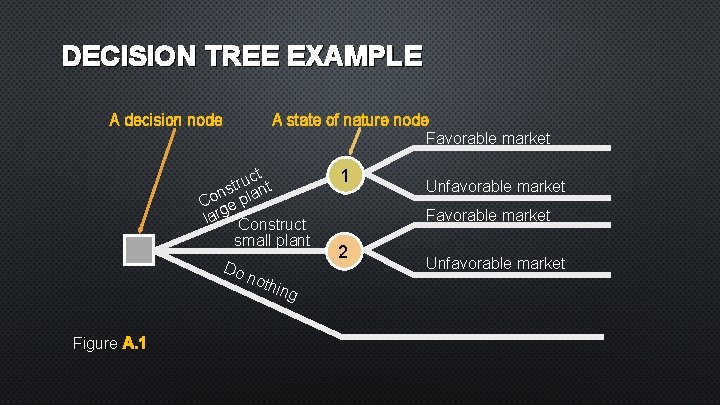
FUNDAMENTALS OF DECISION MAKING 2. Symbols used in a decision tree: a. – Decision node from which one of several alternatives may be selected b. – A state-of-nature node out of which one state of nature will occur

DECISION TREE EXAMPLE A state of nature node Favorable market A decision node uct t r t ns plan o C ge lar Construct small plant Do Figure A. 1 not hin g 1 Unfavorable market Favorable market 2 Unfavorable market

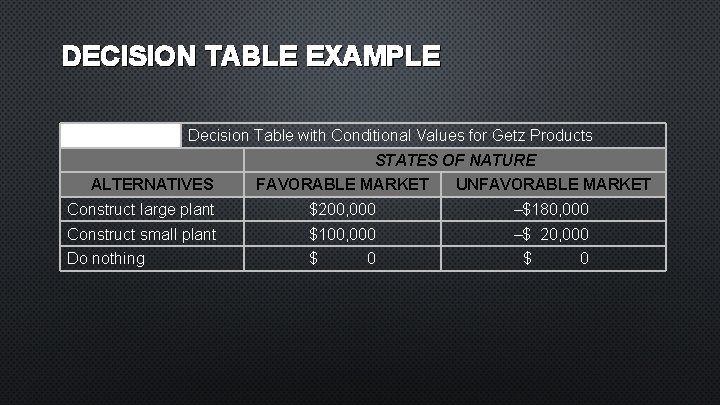
DECISION TABLE EXAMPLE TABLE A. 1 Decision Table with Conditional Values for Getz Products STATES OF NATURE ALTERNATIVES FAVORABLE MARKET UNFAVORABLE MARKET Construct large plant $200, 000 –$180, 000 Construct small plant $100, 000 –$ 20, 000 Do nothing $ 0

DECISION-MAKING ENVIRONMENTS V DECISION MAKING UNDER UNCERTAINTY O COMPLETE UNCERTAINTY AS TO WHICH STATE OF NATURE MAY OCCUR V DECISION MAKING UNDER RISK O SEVERAL STATES OF NATURE MAY OCCUR O EACH HAS A PROBABILITY OF OCCURRING V DECISION MAKING UNDER CERTAINTY O STATE OF NATURE IS KNOWN

UNCERTAINTY 1. MAXIMAX O FIND THE ALTERNATIVE THAT MAXIMIZES THE MAXIMUM OUTCOME FOR EVERY ALTERNATIVE O PICK THE OUTCOME WITH THE MAXIMUM NUMBER O HIGHEST POSSIBLEGAIN O THIS IS VIEWED AS AN OPTIMISTIC DECISION CRITERIA

UNCERTAINTY 2. MAXIMIN O FIND THE ALTERNATIVE THAT MAXIMIZES THE MINIMUM OUTCOME FOR EVERY ALTERNATIVE O PICK THE OUTCOME WITH THE MINIMUM NUMBER O LEAST POSSIBLELOSS O THIS IS VIEWED AS A PESSIMISTICDECISION CRITERIA

UNCERTAINTY 3. EQUALLY LIKELY O FIND THE ALTERNATIVE WITH THE HIGHEST AVERAGE OUTCOME O PICK THE OUTCOME WITH THE MAXIMUM NUMBER O ASSUMES EACH STATE OF NATURE IS EQUALLY LIKELY TO OCCUR

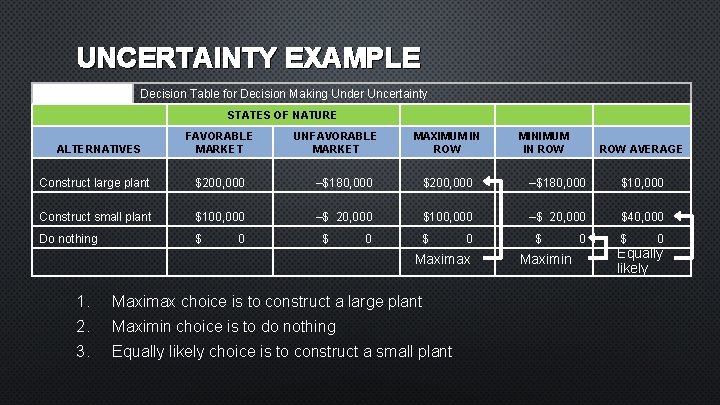
UNCERTAINTY EXAMPLE TABLE A. 2 Decision Table for Decision Making Under Uncertainty STATES OF NATURE ALTERNATIVES FAVORABLE MARKET UNFAVORABLE MARKET MAXIMUM IN ROW MINIMUM IN ROW AVERAGE Construct large plant $200, 000 –$180, 000 $10, 000 Construct small plant $100, 000 –$ 20, 000 $40, 000 Do nothing $ 0 $ 0 Maximax 1. Maximax choice is to construct a large plant 2. Maximin choice is to do nothing 3. Equally likely choice is to construct a small plant $ Maximin 0 $ 0 Equally likely

DECISION MAKING UNDER RISK � EACH POSSIBLE STATE OF NATURE HAS AN ASSUMED PROBABILITY � STATES OF NATURE ARE MUTUALLY EXCLUSIVE � PROBABILITIES MUST SUM TO 1 � DETERMINE THE EXPECTED MONETARY VALUE (EMV) FOR EACH ALTERNATIVE

• MUTUALLY EXCLUSIVE EVENTS: • EVENTS THAT CANNOT OCCUR TOGETHER • COLLECTIVELY EXHAUSTIVE EVENTS: • ONE OF THE EVENTS MUST OCCUR • THE SET OF EVENTS COVERS THE ENTIRE SAMPLE SPACE

EXPECTED MONETARY VALUE EMV (Alternative i) = (Payoff of 1 st state of nature) x (Probability of 1 st state of nature) + (Payoff of 2 nd state of nature) x (Probability of 2 nd state of nature) +…+ (Payoff of last state of nature) x (Probability of last state of nature) MA - 18

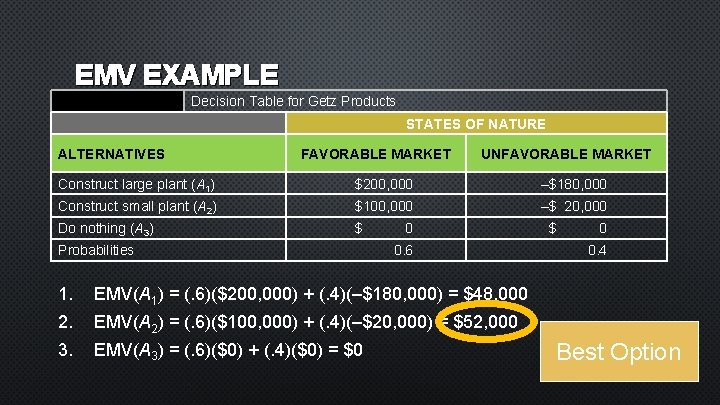
EMV EXAMPLE TABLE A. 3 Decision Table for Getz Products STATES OF NATURE ALTERNATIVES FAVORABLE MARKET UNFAVORABLE MARKET Construct large plant (A 1) $200, 000 –$180, 000 Construct small plant (A 2) $100, 000 –$ 20, 000 Do nothing (A 3) $ Probabilities 1. 2. 3. 0 0. 6 $ 0 0. 4 EMV(A 1) = (. 6)($200, 000) + (. 4)(–$180, 000) = $48, 000 EMV(A 2) = (. 6)($100, 000) + (. 4)(–$20, 000) = $52, 000 EMV(A 3) = (. 6)($0) + (. 4)($0) = $0 Best Option

DECISION MAKING UNDER CERTAINTY O IS THE COST OF PERFECT INFORMATION WORTH IT? O DETERMINE THE EXPECTED VALUE OF PERFECT INFORMATION EVPI ( VPI) E

EXPECTED VALUE OF PERFECT INFORMATION EVPI is the difference between the payoff under certainty and the payoff under risk Maximum EMV EVPI = Expected value with – perfect information Expected value with perfect information (EVw. PI) = (Best outcome or consequence for 1 st state of nature) x (Probability of 1 st state of nature) + Best outcome for 2 nd state of nature) x (Probability of 2 nd state of nature) + … + Best outcome for last state of nature) x (Probability of last state of nature)

EVPI EXAMPLE 1. The best outcome for the state of nature “favorable market” is “build a large facility” with a payoff of $200, 000. The best outcome for “unfavorable” is “do nothing” with a payoff of $0. Expected value with perfect information = ($200, 000)(. 6) + ($0)(. 4) = $120, 000

EVPI EXAMPLE 2. The maximum EMV is $52, 000, which is the expected outcome without perfect information. Thus: EVPI = EVw. PI – Maximum EMV = $120, 000 – $52, 000 = $68, 000 The most the company should pay for perfect information is $68, 000

DECISION TREES O INFORMATION IN DECISION TABLES CAN BE DISPLAYED AS DECISION TREES O A DECISION TREE IS A GRAPHIC DISPLAY OF THE DECISION PROCESS THAT INDICATES DECISION ALTERNATIVES, STATES OF NATURE AND THEIR RESPECTIVE PROBABILITIES, AND PAYOFFS FOR EACH COMBINATION OF DECISION ALTERNATIVE AND STATE OF NATURE O APPROPRIATE FOR SHOWING SEQUENTIAL DECISIONS

DECISION TREES

DECISION TREES 1. Define the problem 2. Structure or draw the decision tree 3. Assign probabilities to the states of nature 4. Estimate payoffs for each possible combination of decision alternatives and states of nature 5. Solve the problem by working backward through the tree computing the EMV for each state-of-nature node

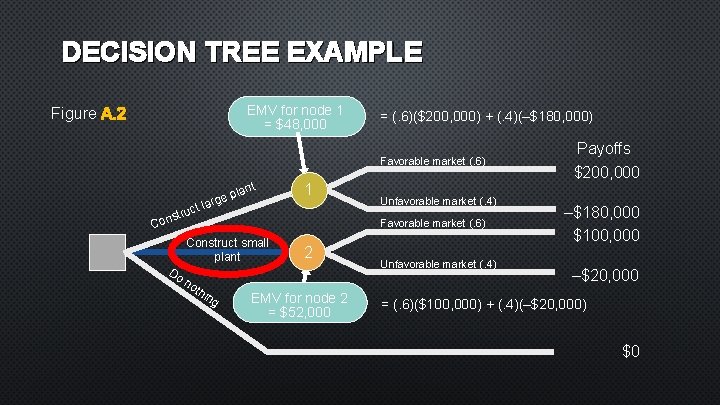
DECISION TREE EXAMPLE EMV for node 1 = $48, 000 Figure A. 2 = (. 6)($200, 000) + (. 4)(–$180, 000) Favorable market (. 6) ge t lar Co lant p 1 uc nstr Do Favorable market (. 6) Construct small plant no thi Unfavorable market (. 4) ng 2 EMV for node 2 = $52, 000 Unfavorable market (. 4) Payoffs $200, 000 –$180, 000 $100, 000 –$20, 000 = (. 6)($100, 000) + (. 4)(–$20, 000) $0

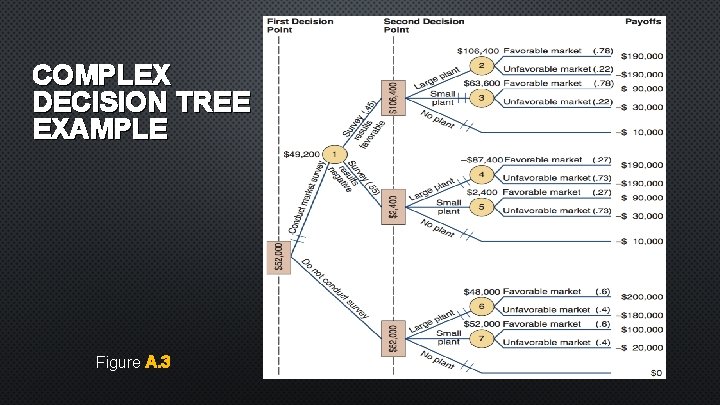
COMPLEX DECISION TREE EXAMPLE Figure A. 3

COMPLEX EXAMPLE 1. Given favorable survey results EMV(2) = (. 78)($190, 000) + (. 22)(–$190, 000) = $106, 400 EMV(3) = (. 78)($90, 000) + (. 22)(–$30, 000) = $63, 600 The EMV for no plant = –$10, 000 so, if the survey results are favorable, build the large plant

COMPLEX EXAMPLE 2. Given negative survey results EMV(4) = (. 27)($190, 000) + (. 73)(–$190, 000) = –$87, 400 EMV(5) = (. 27)($90, 000) + (. 73)(–$30, 000) = $2, 400 The EMV for no plant = –$10, 000 so, if the survey results are negative, build the small plant

COMPLEX EXAMPLE 3. Compute the expected value of the market survey EMV(1) = (. 45)($106, 400) + (. 55)($2, 400) = $49, 200 4. If the market survey is not conducted EMV(6) = (. 6)($200, 000) + (. 4)(–$180, 000) = $10, 000 EMV(7) = (. 6)($100, 000) + (. 4)(–$20, 000) = $40, 000 The EMV for no plant = $0 so, given no survey, build the small plant

COMPLEX EXAMPLE 5. The expected monetary value of not conducting the survey is $52, 000 and the EMV for conducting the study is $49, 200 The best choice is to not seek marketing information and build the small plant

THE POKER DESIGN PROCESS If T. J. folds, The money already in the pot EMV = (. 80)($99, 000) = $79, 200 The chance T. J. will call If T. J. calls, EMV =. 20[(. 45)($853, 000) – Phillips’s bet of $422, 000] =. 20[$383, 850 – $422, 000] =. 20[–$38, 150] = –$7, 630 Overall EMV = $79, 200 – $7, 630 = $71, 750

THE POKER DESIGN PROCESS If If sion i c e d s i The money h t if talready a h t s ld be e u t o T. J. folds, a c w i f d f n o i y pot pathe , 570 ein 1 g not 7 a d r $ i e f d v o e a c V e n ll EM insta es, th EMV = a(. 80)($99, 000) r s m i e i t h v t o y n n i e a one. Th m on t i c s e i e d c r r a e o d m c be the llips’s s i a h w P e h were to= $79, 200 r g cedu thou o r n p e v d E n. a ge calls, analysis The chance T. J. will call T. lar. J. t, his u o k r o w EMV =. 20[(. 45)($853, 000) – Phillips’s bet of $422, 000] =. 20[$383, 850 – $422, 000] =. 20[–$38, 150] = –$7, 630 Overall EMV = $79, 200 – $7, 630 = $71, 750

STEP BY STEP ANALYSIS

STEP BY STEP ANALYSIS PHASE: • STARTING FROM THE RIGHT END OF THE DIAGRAM DECISION AND MOVE BACKWARDS ALONG THE BRANCHES UNTIL IT REACHES A DECISION NODE. • AT THIS DECISION NODE, DID THE SELECTION AMONG ALTERNATIVES EXIST. • ELIMINATE DECISION NODE TO WRITE OFF THE ENTIRE ALTERNATIVE TO THE ALTERNATIVE SELECTED. • FORWARD MOVING BACKWARDS UNTIL IT REACHES THE INITIAL DECISION NODE, AND DO THE SELECTION BETWEEN THE INITIAL ALTERNATIVES.

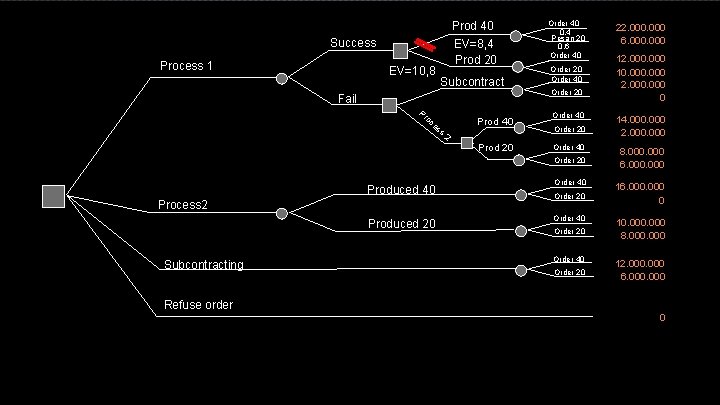
EXAMPLE • IN JUNE 1982, SPAREPARTSFACTORY GOT AN OFFER TO MAKE SPECIAL COMPONENTS, THE PRICE IS 1, 000. MANY ORDERS MAYBE 20 MAYBE 40. THE CERTAINTY ON JANUARY 1983. • THERE ARE 3 WAYS TO PRODUCE: • PROCESS 1: THEY JUST KNOW TO RUN IF SUCCESSFUL PRELIMINARY EXPERIMENT AND TO BE COMPLETED BY SEPT 1982. IF IT FAILS, IT CAN DO THE SECOND, BUT THE INVESTMENT PROCESS 1 WILL BE LOST, ORSUBCONTRACTING • PROCESS 2: MORE SOPHISTICATED AND CERTAINLY SUCCEEDED. • SUBCONTRACTING: IF THE CONTRACT IS NOW CHEAPER, BUT IF AFTER THE JULY 1983 PRICE IS HIGHERS. UBCONTRACTORS CAN MEET WHATEVER THE ORIGIN OF THE ORDER OF NO MORE THAN INJANUARY 1983.

EXAMPLE • BULAN JUNI 1982 PABRIK SUKU CADANG MENDAPAT TAWARAN UNTUK MEMBUAT KOMPONEN KHUSUS, HARGANYARP 1. 000. BANYAK PESANAN MUNGKIN 20 MUNGKIN 40. KEPASTIANNYA BULAN JANUARI 1983. • ADA 3 CARA UNTUK MEMPRODUKSI: • PROSES 1: MEREKA BARU TAHU DPT BERJALAN JIKA SUKSES PERCOBAAN PENDAHULUAN DAN AKAN SELESAI SEPT 1982. JIKA GAGAL, DAPAT DILAKUKAN PROSES 2, TETAPI INVESTASI PROSES 1 AKAN HILANG, ATAU SUBKONTRAK • PROSES 2: LEBIH MUTAKHIR DAN PASTI BERHASIL. • SUBKONTRAK: JIKA KONTRAK DILAKUKAN SEKARANG LEBIH MURAH, TAPI JIKA SETELAH JULI 1983 HARGA LEBIH TINGGIS. UBKONTRAKTOR DAPAT MEMENUHI BERAPA SAJA ASAL PESANAN TIDAK LEBIH DARIJANUARI 1983.

• PROBABILITY OF SUCCESS PROCESS 1 IS 0. 5. AFTER TALKING WITH THE CUSTOMER OPERATIONS MANAGER, THE POSSIBILITY OF ORDERING 40 UNITS WAS 0. 4. • THE PLANNING OF THE PRODUCTION COST IN ACCORDANCE WITH THE PRODUCT DESIGN AS FOLLOWS: • PROCESS 1: EXPERIMENTAL COST PRODUCTION COST/UNIT • PROCESS 2: PRODUCTION COST/UNIT • SUBCONTRACT: (PRICE/UNIT) ORDER LATEST BY JULY ‘ 82 ORDER AUGUST ’ 82 OR THEREAFTER RP RP RP 2. 000 400. 000 600. 000 RP RP 700. 000 900. 000

• KEMUNGKINAN BERHASIL PROSES 1 ADALAH 0, 5. SETELAH MANAJER OPERASI BICARA DENGAN PEMESAN, KEMUNGKINAN MEMESAN 40 UNIT ADALAH 0, 4. • RANCANGAN BIAYA PRODUKSI SESUAI DENGAN DESAIN PRODUK SBB: • PROSES 1: BIAYA PERCOBAAN ONGKOS PRODUKSI/UNT • PROSES 2: ONGKOS PRODUKSI/UNT • SUBKONTRAK: (HARGA/UNIT) PESAN MAX JULI ‘ 82 PESAN AGUS ’ 82 ATAUSSDHNY RP RP RP 2. 000 400. 000 600. 000 RP RP 700. 000 900. 000

• WHEN PRODUCED 20 UNITS, BUT IT TURNS OUT THE ORDER BY 40, THE REMAINDER CAN BE OBTAINED BY SUBCONTRACTING WITH A PRICE RP 900. 000 / UNIT. • IF ALREADY PRODUCED 40 UNITS, AND IT TURNS OUT THE ORDER OF 20 UNITS, THE EXCESS CAN BE SOLD BUT ON PRICE ONLY OF RP 200, 000 / UNIT.

Prod 40 EV=8, 4 Prod 20 Success Process 1 EV=10, 8 Subcontract Fail Pr oc es s Prod 40 2 Prod 20 Order 40 0, 4 Pesan 20 0, 6 Order 40 Order 20 Produced 40 Process 2 Produced 20 Subcontracting Refuse order Order 40 Order 20 22. 000 6. 000 12. 000 10. 000 2. 000 0 14. 000 2. 000 8. 000 6. 000 16. 000 0 10. 000 8. 000 12. 000 6. 000 0

INFORMATION VALUE 1. VALUE OF PERFECT INFORMATION 2. VALUE OF IMPERFECT INFORMATION 3. VALUE OF INFORMATION AND RISK PREFERENCE

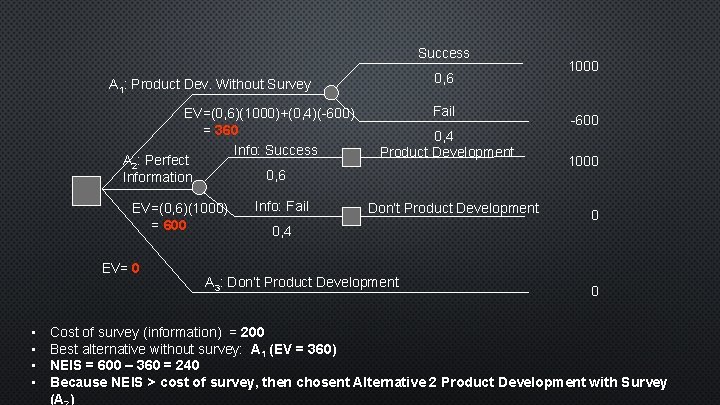
Success 0, 6 A 1: Product Dev. Without Survey EV=(0, 6)(1000)+(0, 4)(-600) = 360 Info: Success A 2: Perfect 0, 6 Information EV=(0, 6)(1000) = 600 EV= 0 • • Info: Fail 0, 4 Product Development Don’t Product Development 1000 -600 1000 0 0, 4 A 3: Don’t Product Development 0 Cost of survey (information) = 200 Best alternative without survey: A 1 (EV = 360) NEIS = 600 – 360 = 240 Because NEIS > cost of survey, then chosent Alternative 2 Product Development with Survey (A )

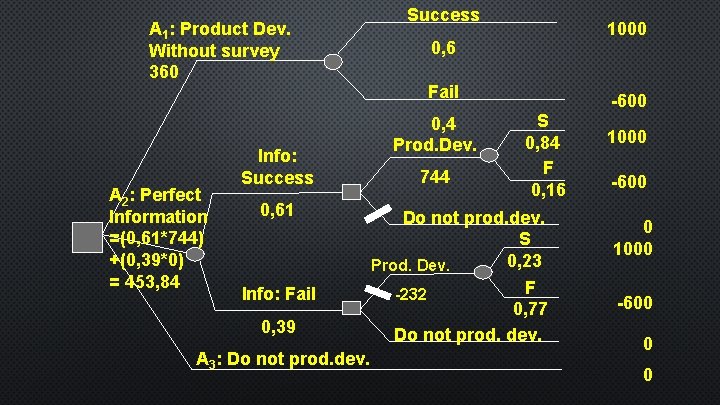
EXPECTED VALUE BASED ON IMPERFECT INFORMATION • COST OF INFORMATION IS RP 200 RATHER THANRP 100 • CAN NOT BE FULLY TRUSTED 100% • IF THE ACTUAL DEVELOPMENT OF SUCCESSFUL, THEN IT IS LIKELY THE RESULTS OF THE SURVEY WOULD SAY SUCCESS IS ONLY 0. 85. CONVERSELY, IF THE ACTUAL DEVELOPMENT FAILS, THE POSSIBILITY OF THE SURVEY RESULTS STATES FAIL 0. 75

A 1: Product Dev. Without survey 360 A 2: Perfect Information =(0, 61*744) +(0, 39*0) = 453, 84 Info: Success 0, 61 Info: Fail 0, 39 A 3: Do not prod. dev. Success 1000 0, 6 Fail 0, 4 Prod. Dev. 744 -600 S 0, 84 F 0, 16 Do not prod. dev. S 0, 23 Prod. Dev. F -232 0, 77 Do not prod. dev. 1000 -600 0 0

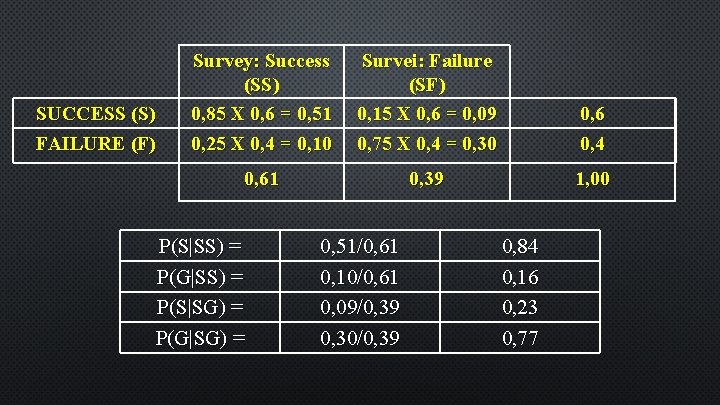
SUCCESS (S) FAILURE (F) Survey: Success (SS) 0, 85 X 0, 6 = 0, 51 0, 25 X 0, 4 = 0, 10 Survei: Failure (SF) 0, 15 X 0, 6 = 0, 09 0, 75 X 0, 4 = 0, 30 0, 6 0, 4 0, 61 0, 39 1, 00 P(S|SS) = P(G|SS) = P(S|SG) = P(G|SG) = 0, 51/0, 61 0, 10/0, 61 0, 09/0, 39 0, 30/0, 39 0, 84 0, 16 0, 23 0, 77

Exercise A natural sports group is studying investments feasibility in the field of rafting. There are three alternatives that can be considered. Alternative A is in the deep river rafting, alternative B is a shallow river rafting, and C alternative is Do Nothing. For alternative A, the value of the investment is not so high, but in terms of marketing is less attractive, because it is considered the value of the challenge is too low, whereas alternative B in terms of marketing is better, but require a higher investment, especially because it must be provided rescuers which is more than alternative A. The alternative A require investment of $ 20, 000. If the marketing success (probability 0. 60) is expected to bring in cash flow equal to the present value of $ 30, 000, but if the marketing fails, only expected to bring in cash flow equal to the present value of $ 18, 000. Alternative B investment value estimated at $ 30, 000. If the marketing success (probability 0. 80) is expected to bring in cash flow equal to the present value of $ 38, 000, but if the marketing fails, only expected to bring in cash flow equal to the present value of $ 25, 000. In evaluating each event in this project, you are asked to base it on the Net Present Value, which is the present value of cash flows less the value of its investment. I want you to: a. Make a decision diagram correctly. b. Choosing which one is the best alternative if used criteria expected value.