Module 5 Relativity of Velocity and Acceleration Velocity

Module 5 Relativity of Velocity and Acceleration Velocity Transforms The velocity transforms follow directly from the Lorentz transform equations, just as the Newtonian velocity transforms follow from the Galilean transforms. Suppose that an object is moving in both frames of reference as shown in Figure 5 -1. Prime and Unprime measure their own respective velocities for the object. Prime sees the object moving at speed u’ in some direction and Unprime sees the object moving at speed u in a different direction. To find how the speeds and directions compare, it is easiest to first find how the components of the velocities compare. As you did in the Problem 1. 1 in Module 1, we start with the definition of velocity and use the chain rule to write y S y’ S’ v O z z’ Module 5 (5. 1) ® u’ ® u x O’ x’ Fig. 5 -1 Relativity of Velocity and Acceleration 1

We now see the impact of the relativity of time. Unlike in Newtonian relativity, dt/dt’ is no longer unity. From the inverse transform for t, Eq. (4. 2), we find (5. 2) You will show in Problem 5. 1 that, upon substituting Eq. (5. 2) and the transforms for x’, y’, and z’ into Eq. (5. 1), the velocity transformation equations are (5. 3) The ux is not a misprint in the denominator of u’y and u’z. The relative motion of the observers affects the measured components of the object’s velocity that are both parallel and perpendicular to the direction of the relative motion. Recall that this is not the case in Newtonian relativity. There, only the parallel component is affected. The reason for this is once again the relativity of time. Velocity is displacement divided by time. Thus, all components of the velocity are different for the two observers. However, if the relative speed between the two observers is low, these differences are negligible. As we expect, if v/c << 1 then ~ 1 and Eqs. (5. 3) reduce to the Newtonian relativity velocity transforms in Eqs. (1. 2). (You should verify this. ) The inverse velocity transform equations can easily be obtained from those in Eqs. (5. 3) by swapping primed and unprimed variables and replacing v with –v. Module 5 Relativity of Velocity and Acceleration 2

We can now compare the speeds of the object measured by the two observers since the speeds are given by and (5. 4) The directions of the respective velocity vectors can also be found from the components and compared. For instance, if the object is confined to two-dimensional travel in the common xy-x’y’ plane, then the angles of the velocity vectors with the relative axis of motion (the common x-x’ axis) are given by and (5. 5) For three-dimensional motion out of this plane, we can calculate and compare azimuthal angles measured from the z and z’ axes in addition to the above polar angles. Finally, we can calculate the angle between the two velocity vectors by making use of the dot product. If we call this angle then (5. 6) Module 5 Relativity of Velocity and Acceleration 3

Acceleration Transforms We play the same derivative game with the velocity components of the object to obtain the acceleration components of the object measured by the two observers. (5. 7) We transform the velocity components with Eqs. (5. 3) and the time derivative with Eq. (5. 2). We then do lots of algebra. The results that we get are (5. 8) We see that the two observers do not measure the same acceleration for the object as in Newtonian relativity. But this does not mean that the laws of mechanics are not invariant in special relativity. The laws of mechanics will hold in each frame of reference. Both observers will see energy and momentum conserved. Module 5 Relativity of Velocity and Acceleration 4

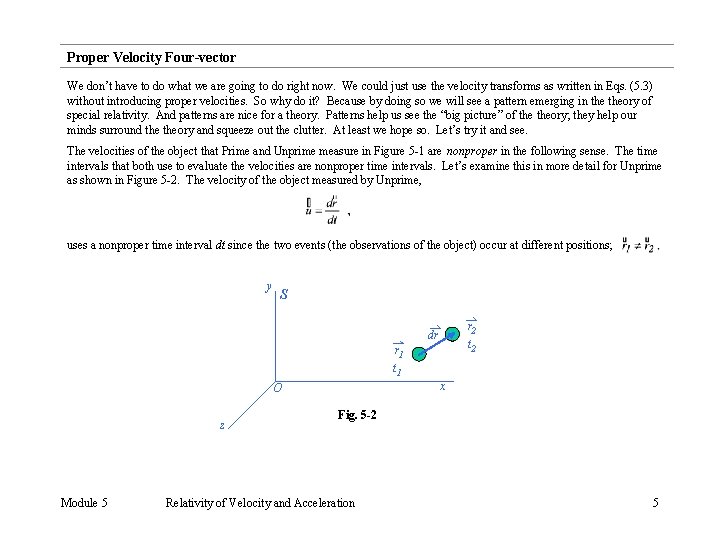
Proper Velocity Four-vector We don’t have to do what we are going to do right now. We could just use the velocity transforms as written in Eqs. (5. 3) without introducing proper velocities. So why do it? Because by doing so we will see a pattern emerging in theory of special relativity. And patterns are nice for a theory. Patterns help us see the “big picture” of theory; they help our minds surround theory and squeeze out the clutter. At least we hope so. Let’s try it and see. The velocities of the object that Prime and Unprime measure in Figure 5 -1 are nonproper in the following sense. The time intervals that both use to evaluate the velocities are nonproper time intervals. Let’s examine this in more detail for Unprime as shown in Figure 5 -2. The velocity of the object measured by Unprime, uses a nonproper time interval dt since the two events (the observations of the object) occur at different positions; y S r 2 t 2 dr r 1 t 1 x O z Module 5 Fig. 5 -2 Relativity of Velocity and Acceleration 5

In fact, any observer that sees the object change position is going to use a nonproper time interval and measure a nonproper velocity. But what about if we use the object’s clock to measure the time difference? The object’s clock measures the proper time interval between the events because in the object’s frame of reference the object doesn’t move. All other frames are moving past it. Let’s call this proper time interval dtp. Then, by the principle of time dilation, we know that (5. 9) where (5. 10) Note that this “eta factor” is just the “gamma factor” between the observer's frame of reference and the object’s frame of reference. If we now define the proper velocity* of the object in frame S to be (5. 11) then, by the use of Eq. (5. 9), we can write or (5. 12) Each component of the proper velocity is the product of the eta factor and the corresponding component of the nonproper velocity: (5. 13) * It is a bit strange to define a velocity this way. We use a displacement measured in one frame and a time interval measured in another frame. One of the results of this mixture is that it is possible for components of proper velocity to be greater than the speed of light. This is okay. The proper velocity is not actually observed by any one. It is a mathematical concoction. Module 5 Relativity of Velocity and Acceleration 6

Now let’s shift our focus to Prime in frame S’. Prime also measures a nonproper velocity for the object given by (5. 14) where the eta factor between Prime and the object is (5. 15) In component form, (5. 16) We now want to relate the two proper velocities with a set of transformation equations, analogous to Eqs. (5. 3) which relate the nonproper velocities. Doing this is straight forward but a bit of an algebraic mess. But the results are worth it so let’s roll up our sleeves and at least do the algebra for the x and x’ components. (5. 17) Into this expression we substitute Eq. (5. 4) for the speed u’ to find (5. 18) Module 5 Relativity of Velocity and Acceleration 7

We now use the velocity transforms for each component from Eqs. (5. 3), (5. 19) We replace 2 with 1 / (1 -v 2/c 2) and multiply numerator and denominator by (1 – vux/c 2) to get (5. 20) Once the terms in parentheses under the radical sign are multiplied out, we collect terms to yield (5. 21) We recognize the sum of the squares of the velocity components in the denominator as the square of the speed u so (5. 22) Module 5 Relativity of Velocity and Acceleration 8

The denominator can be rewritten to give (5. 23) The first term in Eq. (5. 23) is the gamma factor between the two observers. The second term is the eta factor between Unprime and the object so we can write (5. 24) Finally, we multiply through by the eta factor to write (5. 25) Similar analyses (which you are welcome to do) on the other two components of the proper velocities show that (5. 26) The fact that the respective components of the proper velocities perpendicular to the relative motion are equal while those of the nonproper velocities are not (u’y uy and u’z uz) is worthy of comment. Recall that it is the relativity of time that causes the nonproper perpendicular components to disagree. But the proper velocities measured by Prime and Unprime both use the same proper time interval so we expect the agreement of Eqs. (5. 26). But then why doesn’t x equal ’x? Don’t these components also use the same proper time interval? Yes, but the spatial intervals dx and dx’ are not the same because of the relative motion. Thus, ’x x. Module 5 Relativity of Velocity and Acceleration 9

One last algebraic binge can be done to compare the two eta factors. Why do this? We need this result to see the pattern that was mentioned at the beginning of this section. The result is (5. 27) Let us write the four transformation equations together for easier viewing: (5. 28) Let us now add a fourth component to Unprime’s proper velocity vector of the form ic o and a fourth component to Prime’s proper velocity vector of the form ic ’o. We have created a new four-vector in each frame, called the proper velocity fourvector. The four-vectors are expressed as (5. 29) The transformation equations (5. 28) relate the components of the four-vectors. But wait! Lo and behold, these transformation equations can be succinctly written as (5. 30) where L is the same Lorentz operator that transforms the space-time four-vectors discussed in Module 3! The matrix form of the operator is given in Eq. (3. 20). Module 5 Relativity of Velocity and Acceleration 10

But that is not the only similarity between the space-time and proper velocity four-vectors. Recall that the magnitude of a space-time four-vector is invariant. The operator L only rotates a vector into a new direction. Guess what? Yes, the magnitude of a proper velocity four-vector also is invariant in special relativity. You will show in a homework problem that all proper velocity four-vectors have a magnitude of ic The pattern of four-vectors has emerged. Can we make the pattern stronger by finding another invariant four-vector with some connection to measurable physical quantities? Wait and see. Module 5 Relativity of Velocity and Acceleration 11