Module 4 multiple regression and correlation coefficient analysis

Module 4 multiple regression and correlation coefficient analysis Wei Metropolitan State University

Learning objectives and outcomes • Know how to use SPSS to get the multiple regression model (equation) • Know how to test on the slopes of a multiple regression model using SPSS • Know how to create dummy variables • Know how to do collinearity analysis to select predictors • Understand forward selection model, backward selection model and stepwise model • Know how to do residual analysis for multiple regression

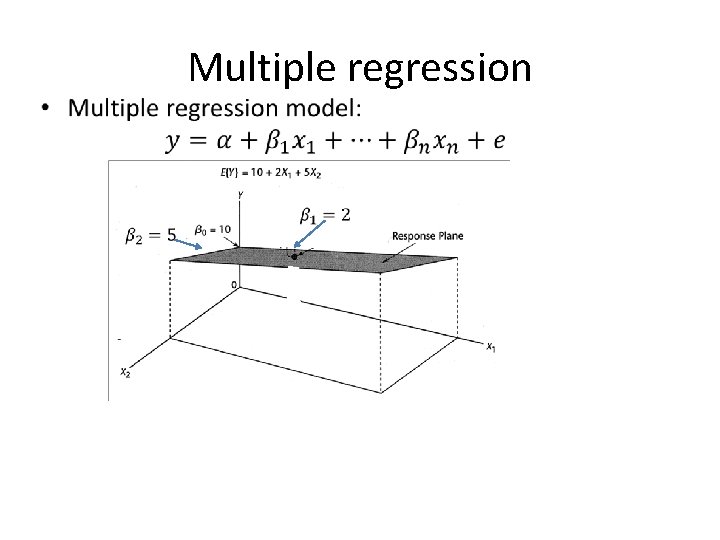
Multiple regression • Want to detect the relationship of the dependent variable with more than one independent variables • Independent variables: – Mix of numeric and dichotomous categorical; – All of them can be numeric

Multiple regression •

Multiple regression • Estimate parameters – Analyze->Regression->Linear->choose your dependent and independent variables

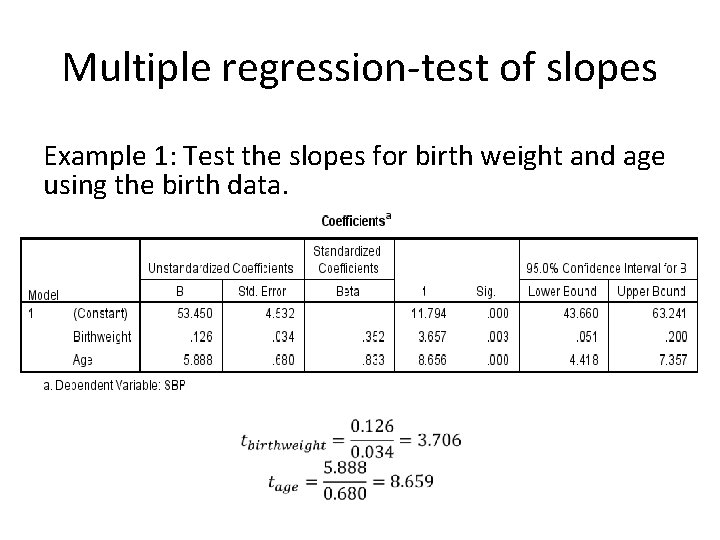
Multiple regression • Example 1: Use the birth data online, SBP is the dependent variable measured by mm. Hg, birth weight is a factor (independent variable) measured by ounces, and age is another independent variable measured by days. – estimate the regression line of relationship between SBP and the two factors – What is the predicted average SBP of a baby with birthweight 128 oz measured at 3 days of life – Interpret the slope for age

Multiple regression • Activity 1: We would like to investigate the relationship between the dependent variable, birth weight (gram), and independent variables, gestational age (week), and length (cm), for low birthweight infants. The data is given online, named “pre-mature infants data”. a) Estimate the multiple regression line for the relationship between birth weight (DV) and the factors of length and gestational age b) Interpret the slope for length

Multiple regression-test of slopes •

Multiple regression-test of slopes Example 1: Test the slopes for birth weight and age using the birth data.

Multiple regression-test of slopes • Activity 2: Use the low birth weight data from activity 1; Test on the slopes of gestational age and length; What are your conclusions? (List the test statistic, p-value and draw your conclusion for each relationship/slope)

What do we use Regression for? • The Target Case Story

Dummy variable •

Multiple regression with dummy variable • Example 3: Test the relationship between SBP and gender, age, and birth weight. Gender 0 represents male and 1 represents female. What do you conclude? • Interpret the slope for gender – When age and birth weight are fixed, on average the SBP for female is 0. 855 mm. Hg lower than male.

Multiple regression with dummy variable • Activity 3: Test the relationship between birth weight and the four independent variables. What can you conclude?

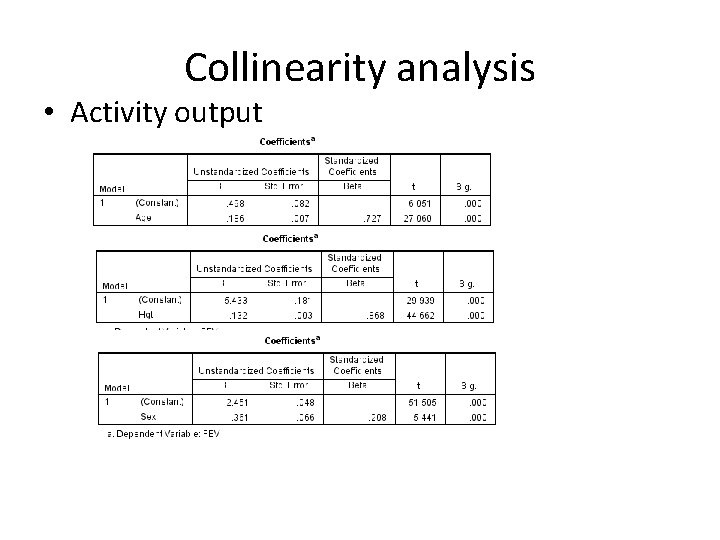
Collinearity analysis Activity 4: Refer to Data Set FEV. DAT online. The forced expiratory volume (FEV, 用力呼 气量) is a good measurement for pulmonary function (肺功能). Possible important determinants of lung function in children are height and age. In the FEV data, the variable age is measured in years, FEV is measured in liters, Hgt represents height and measured in inches. The variable sex is dichotomous, and 0 represents female and 1 represents male. The variable smoke represents the smoking status where 0 represents non-current smoker and 1 represents current smoker. • Consider the variable age only, perform a simple linear regression analysis to assess whethere is a significant relationship between FEV and age. (State the T-statistic, P-value and conclusion) • Consider the variable height only, perform a simple linear regression analysis to assess whethere is a significant relationship between FEV and height. (State the Tstatistic, P-value and conclusion) • Consider the variable sex only, perform a simple linear regression analysis to assess whethere is a significant relationship between FEV and sex. (State the T-statistic, p-value and conclusion)

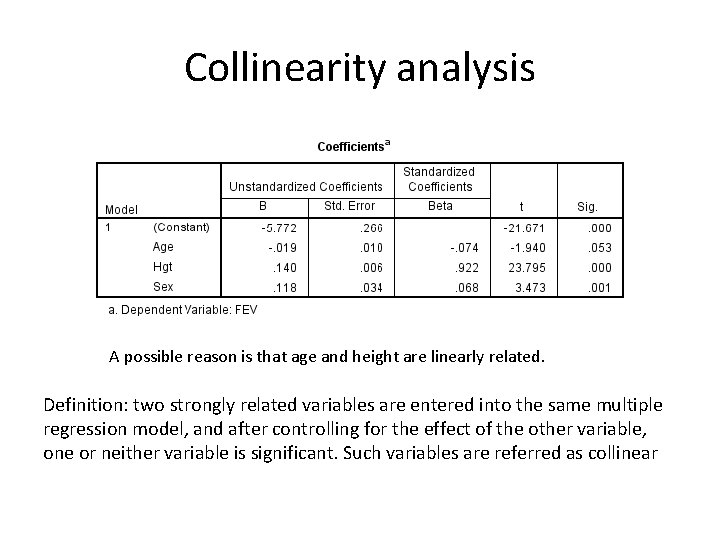
Collinearity analysis • Continue with the activity, consider all three variables together and perform a multiple regression to assess the relationship between FEV and age, height, and sex. (State the Tstatistics, p-values for all three independent variables and state the overall conclusion)

Collinearity analysis • Activity output

Collinearity analysis A possible reason is that age and height are linearly related. Definition: two strongly related variables are entered into the same multiple regression model, and after controlling for the effect of the other variable, one or neither variable is significant. Such variables are referred as collinear

Collinearity analysis •

Collinearity analysis • How to deal with collinear variables? – Remove the least significant one – Construct a linear combination of collinear variables and enter the linear combination in the model

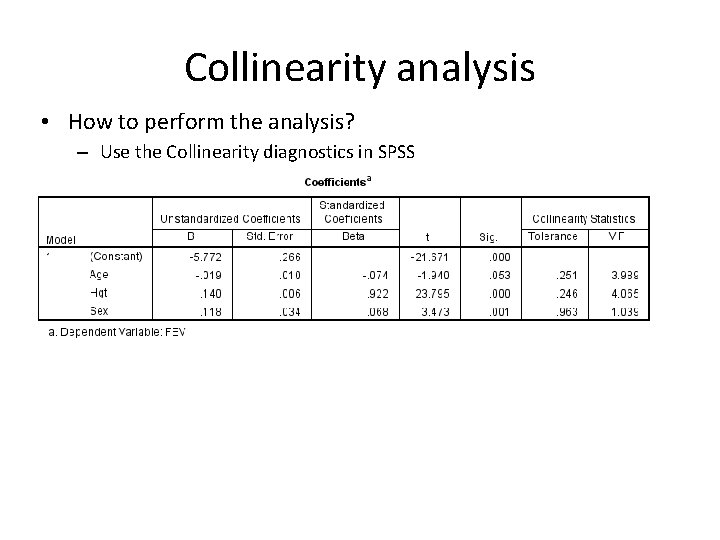
Collinearity analysis • How to perform the analysis? – Use the Collinearity diagnostics in SPSS

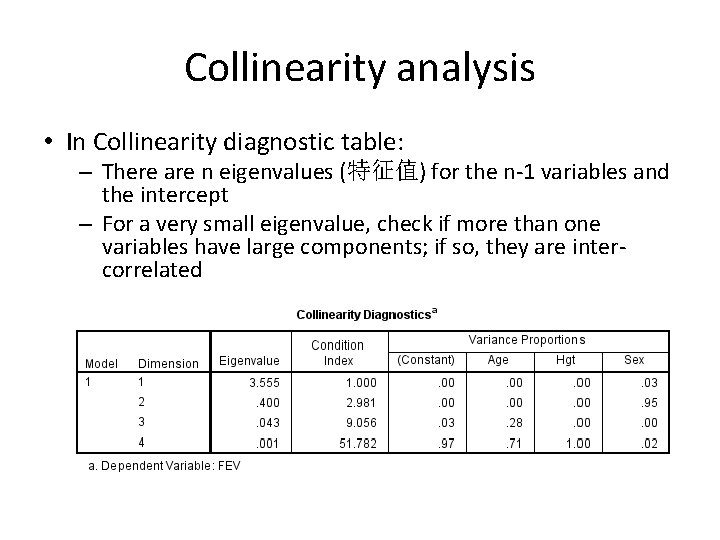
Collinearity analysis • In Collinearity diagnostic table: – There are n eigenvalues (特征值) for the n-1 variables and the intercept – For a very small eigenvalue, check if more than one variables have large components; if so, they are intercorrelated

Model selection •

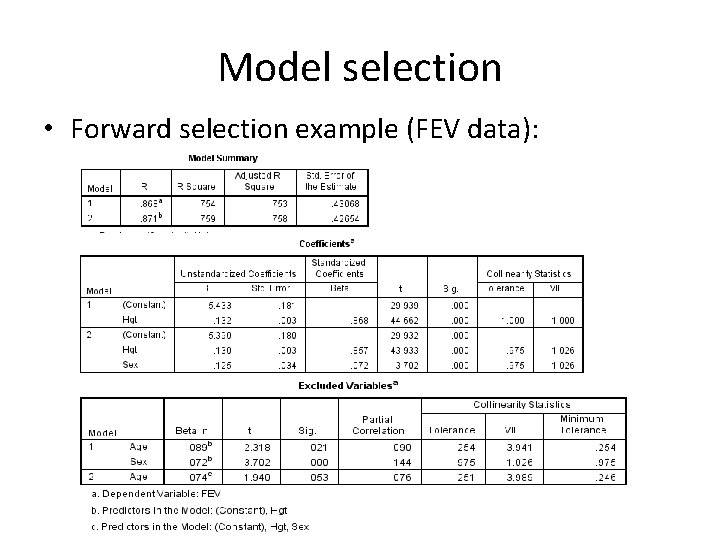
Model selection • Forward selection example (FEV data):

Model selection •

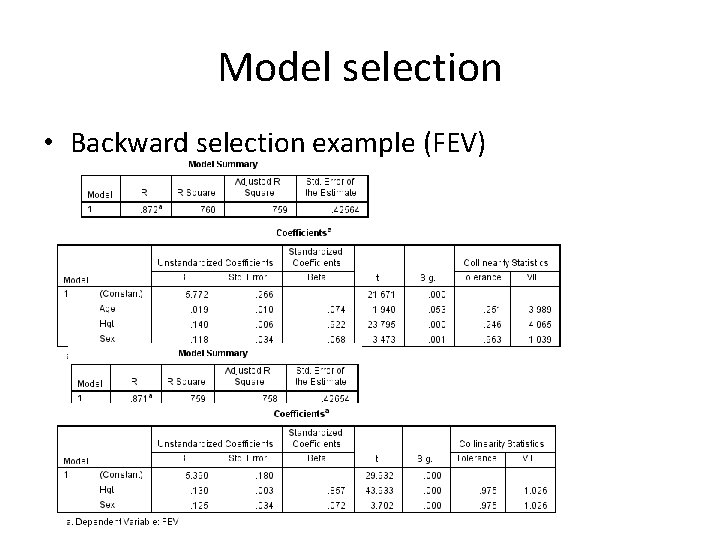
Model selection • Backward selection example (FEV)

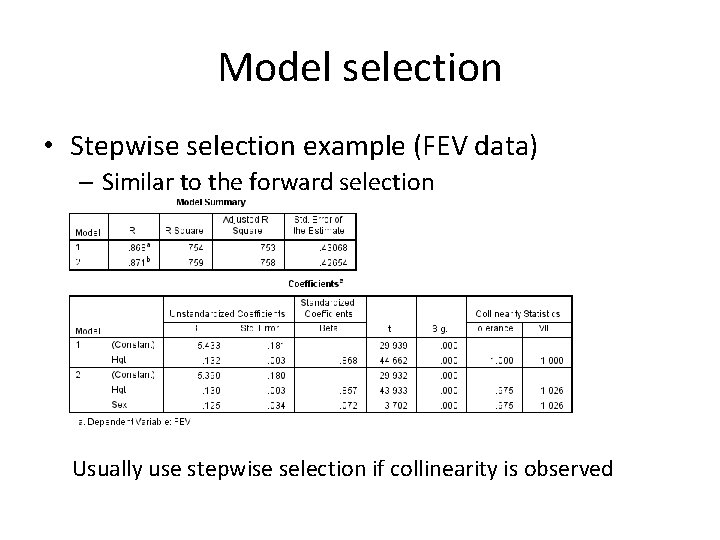
Model selection • Stepwise selection example (FEV data) – Similar to the forward selection Usually use stepwise selection if collinearity is observed

Residual analysis • Similar to the simple linear regression, there are three assumptions to run the multiple regression – Linearity – Equal variances – Normality

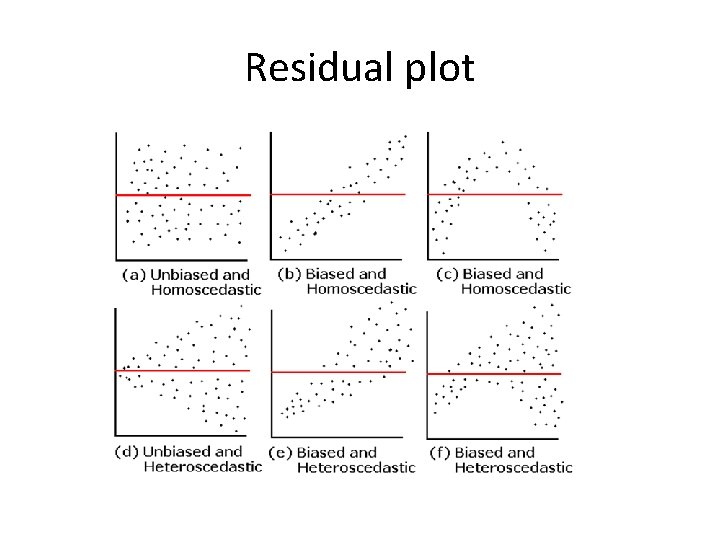
Residual analysis • Residual plot can help us to determine the linearity and equal variance assumption • The normality assumption needs Q-Q plot or test of normality

Residual plot

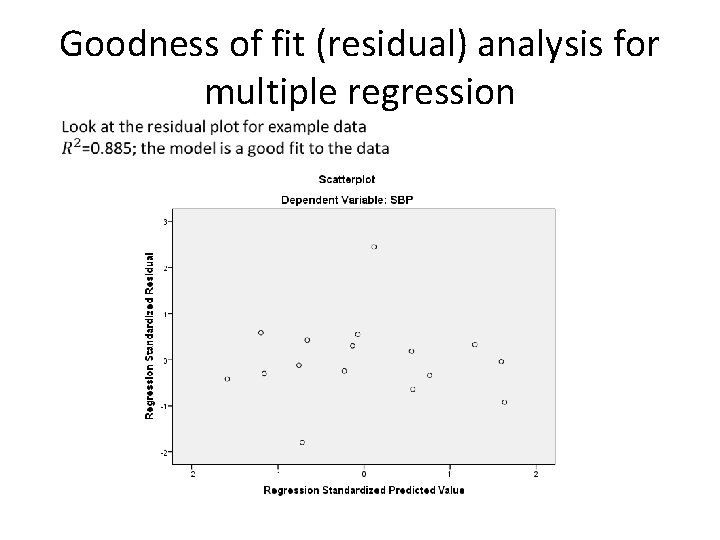
Goodness of fit (residual) analysis for multiple regression

Lead Case Study •