Module 4 Functions Lecture adapted from CS 3511

Module #4 - Functions Lecture adapted from CS 3511, Discrete Methods Kees van Deemter Slides originally adapted from Michael P. Frank’s Course Based on the Text Discrete Mathematics & Its Applications (5 th Edition) by Kenneth H. Rosen 1/22/2022 Michael P. Frank / Kees van Deemter 1

Module #4 - Functions Adaptation of Module #4: 1. Functions Rosen 5 th ed. , § 1. 8 ~45 slides, ~1 lecture 1/22/2022 Michael P. Frank / Kees van Deemter 2

Module #4 - Functions • From calculus, you know the concept of a realvalued function f, which assigns to each number x R one particular value y=f(x), where y R. • Example: f defined by the rule f(x)=x 2 • The notion of a function can be generalized to the concept of assigning elements of any set to elements of any set. • Functions are also called operators. 1/22/2022 Michael P. Frank / Kees van Deemter 3

Module #4 - Functions • Functions were the key concept in lambda calculus and Haskell: • x. x+2 is the function that sends any appropriate argument x to the corresponding value x+2 • After the Haskell definition f x = x+2, f denotes that same function x. x+2 • Let’s be more precise about functions, working towards a classification of functions 1/22/2022 Michael P. Frank / Kees van Deemter 4

Module #4 - Functions Function: Formal Definition • A function f from (or “mapping”) A to B (f: A B) is an assignment of exactly one element f(x) B to each element x A. • Generalizations: – Functions of n arguments: f: (A 1 x A 2. . . x An) B. – A partial (non-total) function f assigns zero or one elements of B to each element x A. 1/22/2022 Michael P. Frank / Kees van Deemter 5

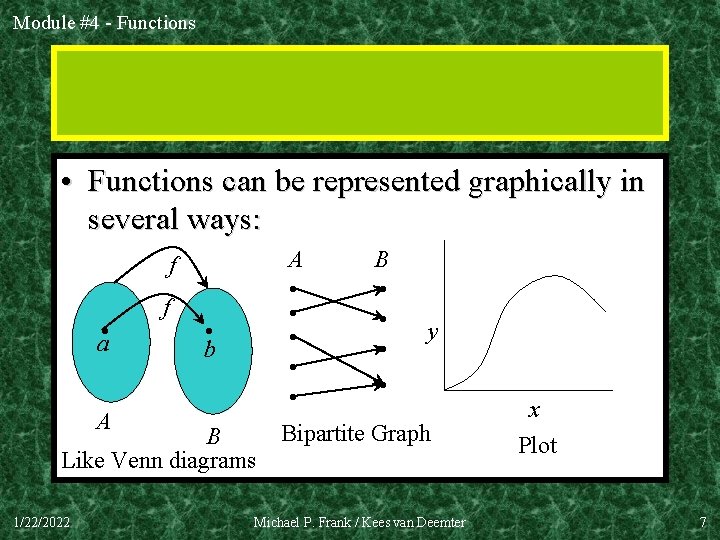
Module #4 - Functions Graphs of Functions • We can represent a function f: A B as a set of ordered pairs f ={(a, f(a)) | a A}. • This makes f a relation between A and B: f is a subset of A x B. But functions are special: – for every a A, there is at least one pair (a, b). Formally: a A b B((a, b) f) – for every a A, there is at most one pair (a, b). Formally: a, b, c((a, b) f (a, c) f b c) • A relation over numbers can be represent as a set of points on a plane. (A point is a pair (x, y). ) – A function is then a curve (set of points), with only one y for each x. 1/22/2022 Michael P. Frank / Kees van Deemter 6

Module #4 - Functions • Functions can be represented graphically in several ways: f a • A f • b B Like Venn diagrams 1/22/2022 A B • • y • • • Bipartite Graph Michael P. Frank / Kees van Deemter x Plot 7

Module #4 - Functions that you’ve seen before • A set S over universe U can be viewed as a function from the elements of U to … 1/22/2022 Michael P. Frank / Kees van Deemter 8

Module #4 - Functions Still More Functions • A set S over universe U can be viewed as a function from the elements of U to … … {T, F}, saying for each element of U whether it is in S. (This is called the characteristic function of S) Suppose U={0, 1, 2, 3, 4}. Then S={1, 3} S(0)=S(2)=S(4)=F, S(1)=S(3)=T. 1/22/2022 Michael P. Frank / Kees van Deemter 9

Module #4 - Functions Still More Functions • A set operator, such as or , can be viewed as a function from … to … 1/22/2022 Michael P. Frank / Kees van Deemter 10

Module #4 - Functions Still More Functions • A set operator such as or can be viewed as a function … … from (ordered) pairs of sets, to sets. – Example: (({1, 3}, {3, 4})) = {3} 1/22/2022 Michael P. Frank / Kees van Deemter 11

Module #4 - Functions A new notation • Sometimes we write YX to denote the set F of all possible functions f: X Y. • Thus, f YX is another way of saying that f: X Y. • (This notation is especially appropriate, because for finite X, Y, we have |F| = |Y||X|. ) 1/22/2022 Michael P. Frank / Kees van Deemter 12

Module #4 - Functions Some Function Terminology • If f: A B, and f(a)=b (where a A & b B), then we say: – A is the domain of f. – B is the codomain of f. – b is the image of a under f. – a is a pre-image of b under f. We also say the signature of f is A→B. • In general, b may have more than 1 pre-image. – The range R B of f is R={b | a f(a)=b }. 1/22/2022 Michael P. Frank / Kees van Deemter 13

Module #4 - Functions Range versus Codomain • The range of a function may not be its whole codomain. • The codomain is the set that the function is declared to map all domain values into. • The range is the particular set of values in the codomain that the function actually maps elements of the domain to. • (The range is the smallest set that could be used as its codomain. ) 1/22/2022 Michael P. Frank / Kees van Deemter 14

Module #4 - Functions Choosing the right (co)domain Consider the function f = λx. 100/x Is f a (total) function from Int to R? • f is a partial function from Int to R • f is a (total) function from Int-{0} to R Consider g = λx. √x Is g a (total) function from R to R? g is a total function from R+ to Rx. R e. g. g(4)= (2, -2) 1/22/2022 Michael P. Frank / Kees van Deemter 15

Module #4 - Functions Images of Sets under Functions • Given f: A B, and S A, • The image of S under f is the set of all images (under f) of the elements of S. f(S) : {f(s) | s S} : {b | s S: f(s)=b}. • The range of f equals the image (under f) of. . . 1/22/2022 Michael P. Frank / Kees van Deemter 16

Module #4 - Functions Images of Sets under Functions • Given f: A B, and S A, • The image of S under f is the set of all images (under f) of the elements of S. f(S) : {f(s) | s S} : {b | s S: f(s)=b}. • The range of f equals the image (under f) of f’s domain. 1/22/2022 Michael P. Frank / Kees van Deemter 17

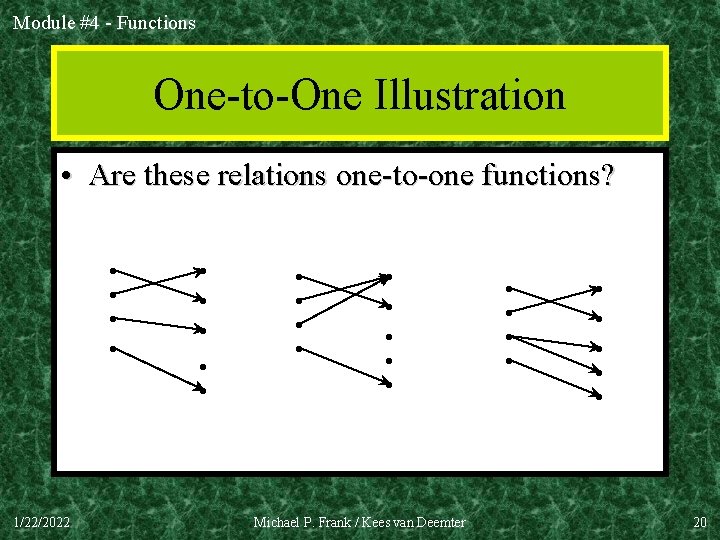
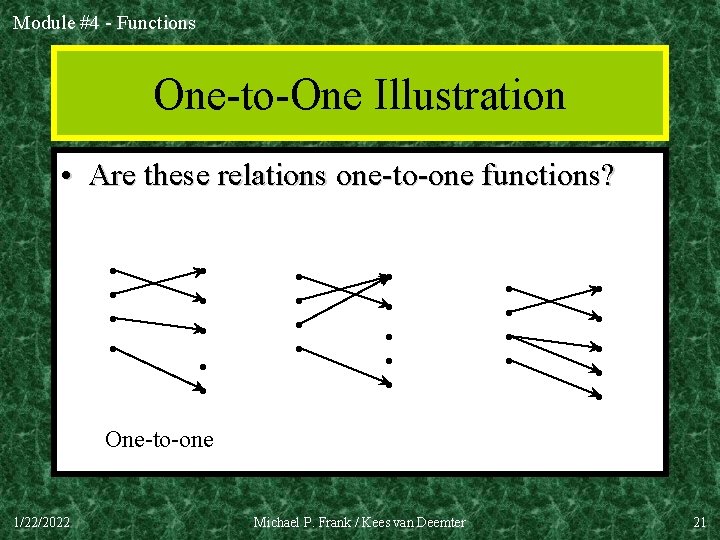
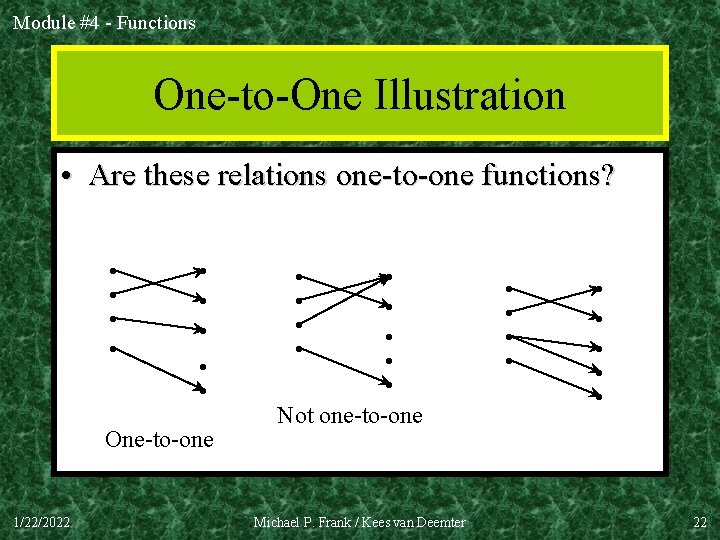
Module #4 - Functions One-to-One Functions • A function is one-to-one (1 -1), or injective, or an injection, iff every element of its range has only 1 pre-image. – Formally: given f: A B, “f is injective” : ( x, y: x y f(x) f(y)). • In other words: only one element of the domain is mapped to any given one element of the range. – In this case, domain & range have same cardinality. What about codomain? 1/22/2022 Michael P. Frank / Kees van Deemter 18

Module #4 - Functions • Codomain may be larger. 1/22/2022 Michael P. Frank / Kees van Deemter 19

Module #4 - Functions One-to-One Illustration • Are these relations one-to-one functions? • • 1/22/2022 • • • • Michael P. Frank / Kees van Deemter • • • 20

Module #4 - Functions One-to-One Illustration • Are these relations one-to-one functions? • • • • • • • One-to-one 1/22/2022 Michael P. Frank / Kees van Deemter 21

Module #4 - Functions One-to-One Illustration • Are these relations one-to-one functions? • • • One-to-one 1/22/2022 • • • Not one-to-one Michael P. Frank / Kees van Deemter • • • 22

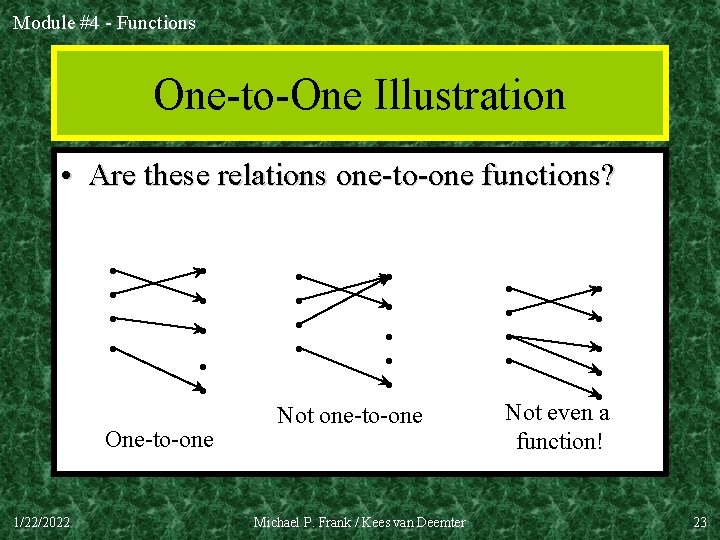
Module #4 - Functions One-to-One Illustration • Are these relations one-to-one functions? • • • One-to-one 1/22/2022 • • • Not one-to-one Michael P. Frank / Kees van Deemter • • • Not even a function! 23

Module #4 - Functions Sufficient Conditions for 1 -1 ness • For functions f over numbers, we say: – f is strictly increasing iff x>y f(x)>f(y) for all x, y in domain; – f is strictly decreasing iff x>y f(x)<f(y) for all x, y in domain; • If f is either strictly increasing or strictly decreasing, then f must be one-to-one. – Does the converse hold? 1/22/2022 Michael P. Frank / Kees van Deemter 24

Module #4 - Functions Onto (Surjective) Functions • A function f: A B is onto or surjective or a surjection iff its range is equal to its codomain ( b B, a A: f(a)=b). • Consider “country of birth of”: A B, where A=people, B=countries. Is this a function? Is it an injection? Is it a surjection? 1/22/2022 Michael P. Frank / Kees van Deemter 25

Module #4 - Functions Onto (Surjective) Functions • A function f: A B is onto or surjective or a surjection iff its range is equal to its codomain • Consider “country of birth of”: A B, where A=people, B=countries. Is this a function? Yes (always 1 c. o. b. ) Is it an injection? No (many have same c. o. b. ) Is it a surjection? Probably yes. . 1/22/2022 Michael P. Frank / Kees van Deemter 26

Module #4 - Functions Onto (Surjective) Functions • A function f: A B is onto or surjective or a surjection iff its range is equal to its codomain • In predicate logic: 1/22/2022 Michael P. Frank / Kees van Deemter 27

Module #4 - Functions Onto (Surjective) Functions • A function f: A B is onto or surjective or a surjection iff its range is equal to its codomain. • In predicate logic: b B a A f(a)=b 1/22/2022 Michael P. Frank / Kees van Deemter 28

Module #4 - Functions Onto (Surjective) Functions • A function f: A B is onto or surjective or a surjection iff its range is equal to its codomain ( b B a A f(a)=b). • E. g. , for domain & codomain Z, the function x. x+1 is injective and surjective. 1/22/2022 Michael P. Frank / Kees van Deemter 29

Module #4 - Functions Claim: if f: Z Z and f = x. x+1 then f is 1 -to-1 and also onto. (Z is the set of all integers) • Proof that f is onto: Consider any arbitrary element a of Z. We have f(a-1)=a, where a Z. • Proof that f is 1 -to-1: Suppose f(u)=f(w)=a. In other words, u+1=a and w+1=a. It follows that u=a -1 and w=a-1, so u=w. 1/22/2022 Michael P. Frank / Kees van Deemter 30

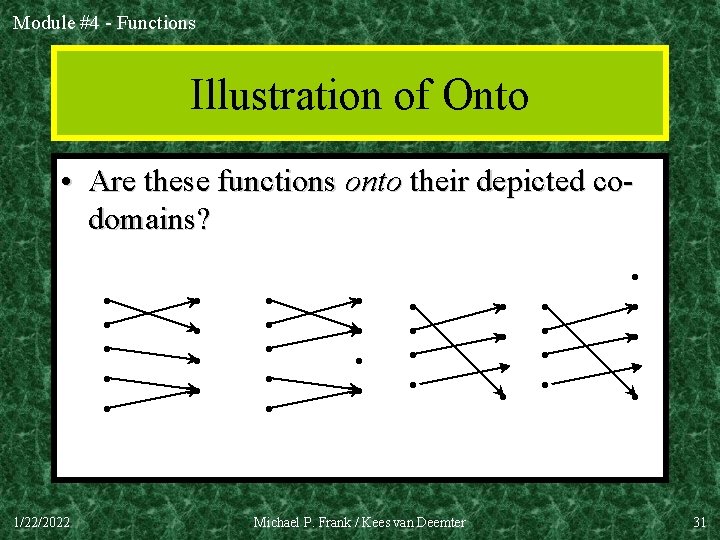
Module #4 - Functions Illustration of Onto • Are these functions onto their depicted codomains? • • • 1/22/2022 • • • • • Michael P. Frank / Kees van Deemter • • • • 31

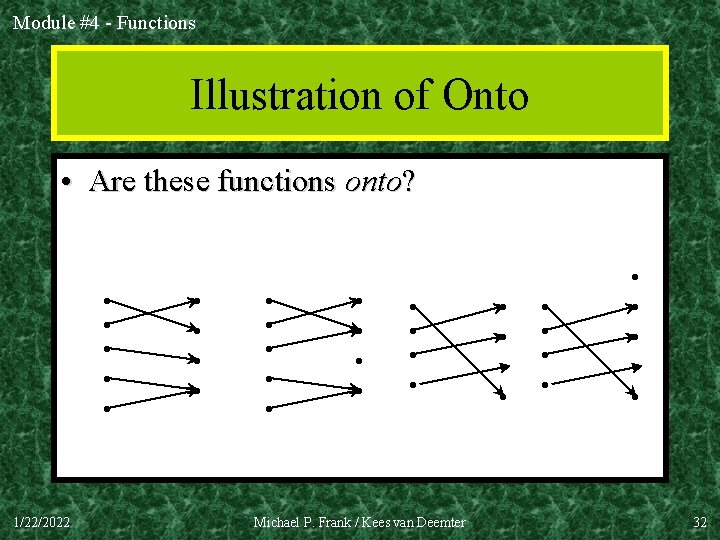
Module #4 - Functions Illustration of Onto • Are these functions onto? • • • 1/22/2022 • • • • • Michael P. Frank / Kees van Deemter • • • • 32

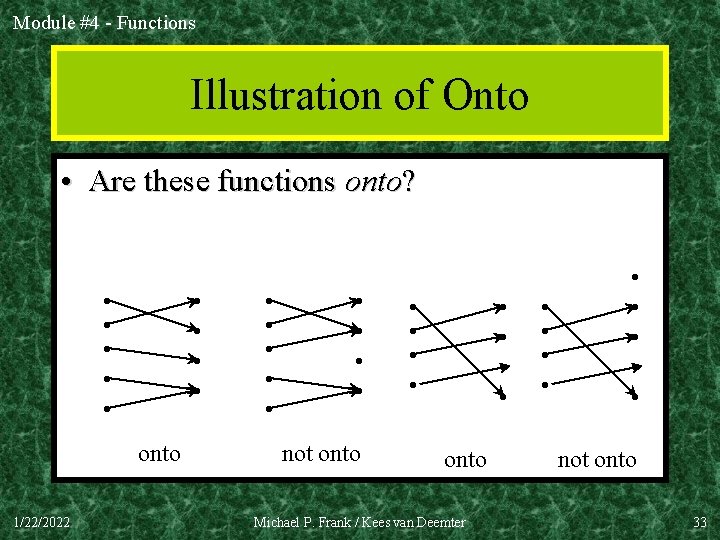
Module #4 - Functions Illustration of Onto • Are these functions onto? • • • onto 1/22/2022 • • • not onto • • onto Michael P. Frank / Kees van Deemter • • • not onto 33

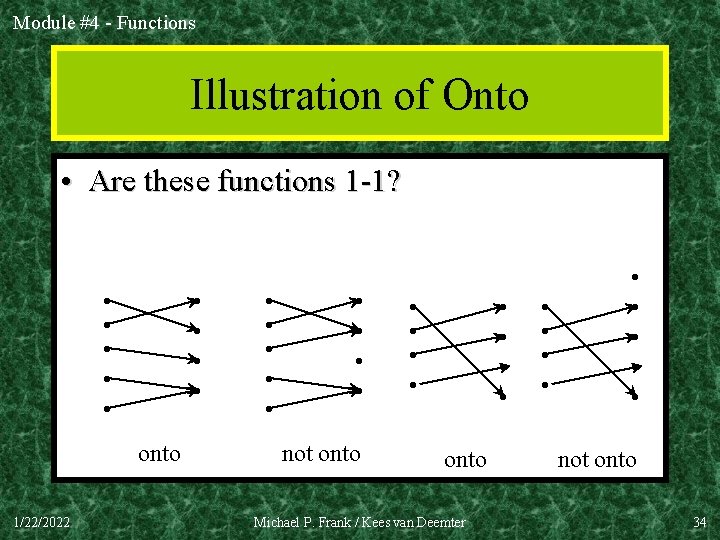
Module #4 - Functions Illustration of Onto • Are these functions 1 -1? • • • onto 1/22/2022 • • • not onto • • onto Michael P. Frank / Kees van Deemter • • • not onto 34

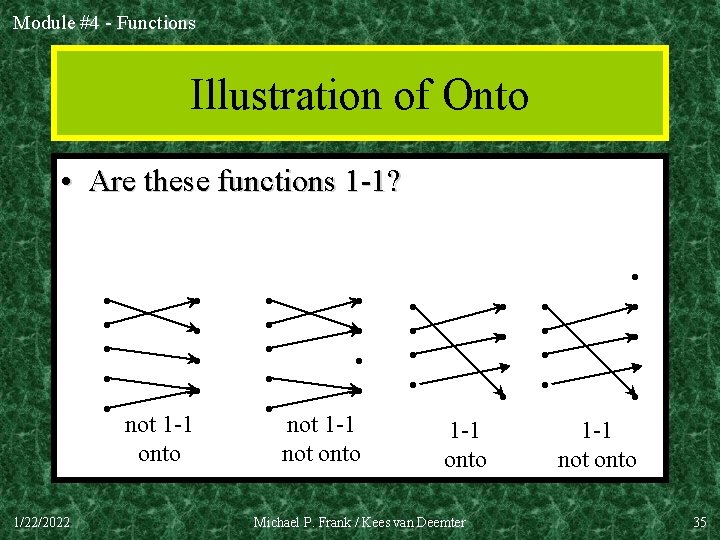
Module #4 - Functions Illustration of Onto • Are these functions 1 -1? • • • 1/22/2022 • • not 1 -1 onto • • • not 1 -1 not onto • • 1 -1 onto Michael P. Frank / Kees van Deemter • • • 1 -1 not onto 35

Module #4 - Functions Bijections • A function is said to be a one-to-one correspondence, or a bijection iff it is both one-to-one and onto. 1/22/2022 Michael P. Frank / Kees van Deemter 36

Module #4 - Functions Two terminologies for talking about functions 1. injection = one-to-one 2. surjection = onto 3. bijection = one-to-one correspondence 3 = 1&2 1/22/2022 Michael P. Frank / Kees van Deemter 37

Module #4 - Functions Bijections • For bijections f: A B, there exists a function that is the inverse of f, written f 1: B A • Intuitively, this is the function that undoes everything that f does • Formally, it’s the unique function such that. . . 1/22/2022 Michael P. Frank / Kees van Deemter 38

Module #4 - Functions Bijections • For bijections f: A B, there exists an inverse of f, written f 1: B A • Intuitively, this is the function that undoes everything that f does • Formally, it’s the unique function such that (the identity function on A) 1/22/2022 Michael P. Frank / Kees van Deemter 39

Module #4 - Functions Bijections • Example 1: Let f: Z Z be defined as f(x)= x+1. What is f 1 ? • Example 2: Let g: Z N be defined as g(x)= |x|. What is g 1 ? 1/22/2022 Michael P. Frank / Kees van Deemter 40

Module #4 - Functions Bijections • Example 1: Let f: Z Z be defined as f(x)=x+1. What is f 1 ? • f 1 is the function (let’s call it h) h: Z Z defined as h(x)=x-1. • Proof: h(f(x)) = (x+1)-1 = x 1/22/2022 Michael P. Frank / Kees van Deemter 41

Module #4 - Functions Bijections • Example 2: Let g: Z N be defined as g(x)=|x|. What is g 1 ? • This was a trick question: there is no such function, since g is not a bijection: There is no function h such that h(|x|)=x and h(|x|)= x • (NB There is a relation h for which this is true. ) 1/22/2022 Michael P. Frank / Kees van Deemter 42

Module #4 - Functions • The Diagonalisation Method Georg Cantor (1873): Can we compare the sizes of infinite sets? • Example: card(N ) = card({0*1*})? – Both are infinite – But is one larger than the other? • Cantor’s idea: – The size (cardinality) of a set should not depend on the identity of its elements – Two finite sets A and B have the same size if we can pair the elements of A with elements of B – Formally: there exists a bijection between A and B 1/22/2022 Michael P. Frank / Kees van Deemter 43

Module #4 - Functions • Example: Let Correspondences (Cont’d) – N be the set of natural numbers {1, 2, 3, …} – E be the set of even natural numbers {2, 4, 6, …} • Using Cantor’s definition of size, we can show that N and E have the same size: n f (n) 1 2 2 4 3 6 • Intuitively, E is smaller than N, but – Pairing each element of N with its corresponding element in E is possible, – So we declare these two set to be the same size … … – Bijection (!): f (n) = 2 n – This even though E N (E is a real subset of N ) 1/22/2022 Michael P. Frank / Kees van Deemter 44

Module #4 - Functions • A set X is finite if it has n elements, Countable sets for some n in N. • A set is countable if either – It is finite or – It has the same size as N, the natural numbers • For example, – N is countable, and so are all its subsets: – E is countable – {0, 1, 2, 3} is countable – is countable • How about supersets of N? 1/22/2022 Michael P. Frank / Kees van Deemter 45

Module #4 - Functions • Let Q be the set of positive rational numbers An Even Stranger Example… Q = { m/n | m, n N } • Just like E, the set Q has the same size as N ! – We show this giving a bijection from Q to N – Q is thus countable • One way is to enumerate (i. e. , to list) X’s elements. For example, for X=Q : – Pair the first element of X with 1 from N And so on, making sure every member of Q appears only once in the list 1/22/2022 Michael P. Frank / Kees van Deemter 46

Module #4 - Functions An Even Example… • To build a list Stranger with the elements of Q – make inf. matrix with all positive rational numbers (Cont’d) – i -th row contains all numbers with numerator i – j -th column has all numbers with denominator j – i /j is in i -th row and j -th column 1/1 1/2 1/3 1/4 1/5 2/1 2/2 2/3 2/4 2/5 3/1 3/2 3/3 3/4 3/5 4/1 4/2 4/3 4/4 4/5 5/1 5/2 5/3 5/4 5/5. . . 1/22/2022 Michael P. Frank / Kees van Deemter 47

Module #4 - Functions Anwe. Even Stranger Example… • Now turn the previous matrix into a list • A bad way: begin(Cont’d) list with first row – Since rows are infinite, we will never get to 2 nd row! 1/22/2022 Michael P. Frank / Kees van Deemter 48

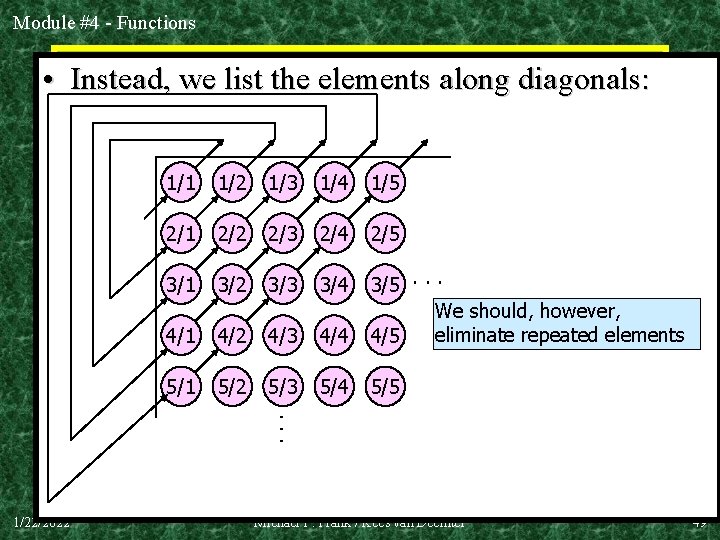
Module #4 - Functions An Even • Instead, we list. Stranger the elements. Example… along diagonals: (Cont’d) 1/2 1/3 1/4 1/5 2/1 2/2 2/3 2/4 2/5 3/1 3/2 3/3 3/4 4/1 4/2 4/3 4/4 3/5. . . We should, however, eliminate repeated elements 4/5 5/1 5/2 5/3 5/4 5/5 . . . 1/1 1/22/2022 Michael P. Frank / Kees van Deemter 49

Module #4 - Functions An Stranger Example… • We list. Even elements along diagonals w/o repetitions: (Cont’d) 1/1 1/2 1/3 1/4 2/1 2/2 2/3 2/4 3/1 3/2 3/3 4/1 4/2 1/5 . . . 1/1, 2/1, 1/2, 3/1, 1/3, … . . . 5/1 1/22/2022 Michael P. Frank / Kees van Deemter 50

Module #4 - Functions Uncountable sets • Some sets have no correspondence with N • These sets are simply too big! – They are not countable: we say uncountable • Theorem: – The set of real numbers between 0 and 1 (e. g. , 0. 244, 0. 3141592323. . ) is uncountable Call this set R 0, 1 (Some sets are even larger. “Serious” set theory is all about theorems that concern infinite sets. – Most of this is irrelevant for this course. ) 1/22/2022 Michael P. Frank / Kees van Deemter 51

Module #4 - Functions Finally: diagonalisation Theorem: | R 0, 1 | > |N|. Proof strategy: | R 0, 1 |>=|N|. Suppose | R 0, 1 |=|N| and derive a contradiction: Each member of R 0, 1 can be written as a zero followed by a dot and a countable sequence of digits. Suppose there existed a complete enumeration of R, (using whatever order) <e 1, e 2, e 3, . . . >. 1/22/2022 Michael P. Frank / Kees van Deemter 52

Module #4 - Functions Cantor’s diagonalisation trick: (starting from an arbitrary list) e 1. 0. 00000000000. . e 2. 0. 010000000000. . e 3. 0. 820000000000. . e 4. 0. 1710000000000. . . . 1/22/2022 Michael P. Frank / Kees van Deemter 53

Module #4 - Functions Now construct a Real number n that’s not in the enumeration: n’s first digit (after the dot) = [e 1’s first digit] + 1 n’s second digit = [e 2’s second digit] + 1. . . General: n’s i-th difit = [e-i’s i-th digit] + 1 i: n differs from e-i in its i-th digit Contradiction: <e 1, e 2, e 3, . . . > is not a (complete) enumeration after all. QED 1/22/2022 Michael P. Frank / Kees van Deemter 54

Module #4 - Functions Adaptation of Module #3: 2. Sets and the Russell Paradox Rosen 5 th ed. , § 1. 6 especially ex. 30 on p. 86 1/22/2022 Michael P. Frank / Kees van Deemter 55

Module #4 - Functions Basic Set Notations • Set enumeration {a, b, c} and set-builder {x|P(x)}. • relation, and the empty set . • Set relations =, , etc. • Venn diagrams. • Cardinality |S| and infinite sets N, Z, R. • Power sets P(S). 1/22/2022 Michael P. Frank / Kees van Deemter 56

Module #4 - Functions Axiomatic set theory • Various axioms, e. g. , saying that the union of two sets is also a set • One key axiom: Given a Predicate P, construct a set. The set consists of all those elements x such that P(x) is true. • But, the resulting theory turns out to be logically inconsistent! – This means, there exist set theory propositions p such that you can prove that both p and p follow logically from the axioms of theory! – The conjunction of the axioms is a contradiction! – This theory is fundamentally uninteresting, because any possible statement in it can be (very trivially) “proved” by contradiction! 1/22/2022 Michael P. Frank / Kees van Deemter 57

Module #4 - Functions This version of Set Theory is inconsistent Russell’s paradox: • Consider the set that corresponds with the predicate x x : S = {x | x x }. • Now ask: is S S? 1/22/2022 Michael P. Frank / Kees van Deemter 58

Module #4 - Functions Russell’s paradox • Let S = {x | x x }. Is S S? • If S S, then S is one of those objects x for which x x. In other words, S S With Proof by Contradiction, we have S S • If S S, then S is not one of those objects x for which x x. In other words, S S With Proof by Contradiction, we have S S • We conclude that both S S nor S S • Paradox! 1/22/2022 Michael P. Frank / Kees van Deemter 59

Module #4 - Functions • To avoid inconsistency, set theory must somehow change 1/22/2022 Bertrand Russell 1872 -1970 Michael P. Frank / Kees van Deemter 60

Module #4 - Functions One technique to avoid the problem: • Given a set S and a predicate P, construct a new set, consisting of those elements x of S such that P(x) is true. • You’ve seen this technique in use: Haskell’s list comprehensions allow us to write [x | x [1. . ] , even x], but not simply [x | even x], 1/22/2022 Michael P. Frank / Kees van Deemter 61

Module #4 - Functions Another technique to avoid the problem: • Russell’s paradox arises from the fact that we can write x x (or x x, for that matter). Forbid such expressions using types. • You’ve seen this technique in use: Haskell’s use of typing. Applied to the present case: give a type that forbids it from relating two things of the same type. 1/22/2022 Michael P. Frank / Kees van Deemter 62

Module #4 - Functions Our focus: computability • We shall not worry about “saving” set theory from paradoxes like Russell’s • Instead, we shall use the Russell paradox in a different setting • Before we do this, we need to talk about computability and Turing Machines. 1/22/2022 Michael P. Frank / Kees van Deemter 63

Module #4 - Functions 1/22/2022 Michael P. Frank / Kees van Deemter 64