Module 3 Special Relativity The Postulates of Special

Module 3 Special Relativity The Postulates of Special Relativity We said in the last module that Scenario 3 is our choice. If so, our first task is to find new transformation equations which are generalizations of the Galilean transformation equations. We will do this by making one assumption and stating two principles. The two principles are often cited when one reads about Einstein’s development of special relativity. The assumption is less well known but absolutely necessary. Don’t worry, it is not a restrictive assumption. It seems a very trivial one. We will assume that space and time are homogeneous. By this, we mean that the laws of physics work equally well no matter where and when we are in the universe. The results of an experiment done on Earth will be predicted by the same laws of physics as the results of the same experiment done in the Andromeda galaxy. We will see the importance of this assumption in our derivation. The two principles are now stated. 1. The Principle of Relativity All the laws of physics are invariant in all inertial frames of reference. There is no special frame. 2. The Principle of the Constancy of the Speed of Light All observers in inertial frames of reference measure the same speed for light. We see that the two principles really just summarize the results of Scenario 3. Let’s now see what follows. Module 3 Special Relativity 1

The Lorentz Transformation Equations We take two frames whose origins coincide at t = t’ = 0 as before. The frame geometry is shown once more in Figure 3 -1. Because of the homogeneity of space and time assumption, we expect that the spatial and temporal coordinates of the two frames depend on one another linearly. (Think about this one for a bit to convince yourself. If this wasn’t true, then the length of a moving object would not only be a function of how fast it’s moving but also a function of where it is in your frame of reference. ) We mathematically state this linear dependence by writing (3. 1) In vector operator form, we can write this as (3. 2) where the operator A can be represented by a four-by-four matrix with elements aij. Our task is to find the values of these matrix elements. y y’ S S’ O z O’ v x’ x z’ Fig. 3 -1 Module 3 Special Relativity 2

First, we conjecture that the spatial components of an event that are perpendicular to the direction of relative motion should not be affected by the relative motion. Since the direction of relative motion is always the common x, x’ axis, this requires that y’ and z’ should not depend on x and t. Thus, a 21 = a 31 = a 24 = a 34 = 0 (3. 3) Along the same line of thinking, we expect that the planes xy and x’y’ will always be the same plane. This means that y’ cannot depend on z. Similarly, the planes xz and x’z’ will always be identical so z’ cannot depend on y. This takes care of two more elements: a 23 = a 32 = 0 (3. 4) At this point, the transformation equations for y’ and z’ are y’ = a 22 y and z’ = a 33 z. Let’s do a little thought experiment. Suppose that we have a rod at rest in frame S aligned along the y-axis. The length of the rod measured by Unprime is one, i. e. y = 1. (You supply your favorite unit of length. ) Prime is moving to the right at speed v relative to Unprime. This is shown in Figure 3 -2(a). Prime measures the rod to have a length of a 22. Now place the same rod so that it is at rest in frame S’ along the y’-axis. Prime will measure a length of one, y’ = 1. Make Unprime move to the left at the same speed v with respect to Prime. This is shown in Figure 3 -2(b). Unprime will measure the rod to have a length of 1/ a 22 since y’ = a 22 y. Now, when the rod is moving at the same speed with respect to two observers, we expect that the two observers will measure the same length for the rod. Thus, we conclude that a 22 = 1/a 22. This demands that a 22 = 1. We can now orient the rod along the z and z’ axes and conclude that a 33 also must be one. a 22 = a 33 = 1 y S y’ (3. 5) S’ v v y S y’ 1 O Module 3 S’ 1 (a) Special Relativity O’ x x’ O Fig. 3 -2 (b) O’ x x’ 3

We stated that spatial components that are perpendicular to the direction of relative motion are unaffected by the motion. We therefore expect that measured times are independent of these perpendicular spatial components. That is, t’ cannot depend on y and z. Thus, a 42 = a 43 = 0 (3. 6) In summary, it is only the relative motion direction that has an effect on time and, of the three spatial components, it is only the spatial component parallel to that direction that is affected. This is consistent with the homogeneity of space and time. If we substitute the elements that we know so far, Eqs. (3. 3) to (3. 6), into Eq. (3. 1), the transformation equations become (3. 7) Recall from the Galilean transformation equations that x’ = x – vt. The value of x – vt is the distance that Unprime sees between the event located at x and the position of the origin O’. We generalize and state that this distance may be different in the new relativity so that (3. 8) Distributing the coefficient b gives (3. 9) Comparing this equation to the first equation in Eqs. (3. 7) we identify that b = a 11 and a 14 = -a 11 v. Thus, the transformation equations become Module 3 Special Relativity 4

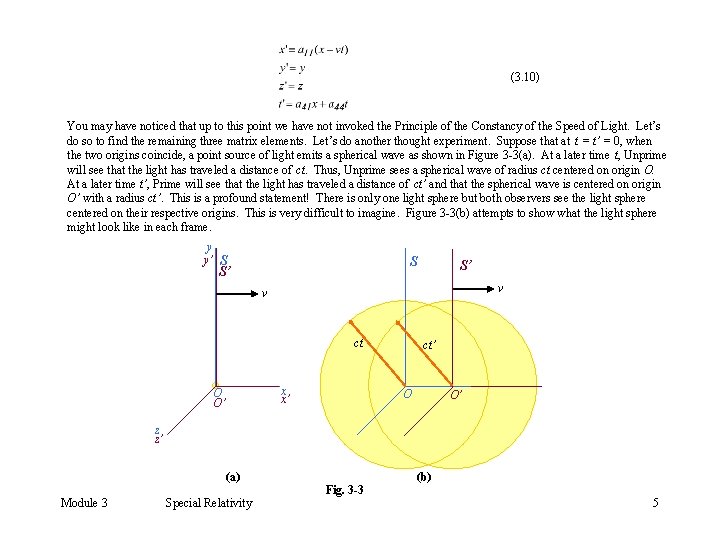
(3. 10) You may have noticed that up to this point we have not invoked the Principle of the Constancy of the Speed of Light. Let’s do so to find the remaining three matrix elements. Let’s do another thought experiment. Suppose that at t = t’ = 0, when the two origins coincide, a point source of light emits a spherical wave as shown in Figure 3 -3(a). At a later time t, Unprime will see that the light has traveled a distance of ct. Thus, Unprime sees a spherical wave of radius ct centered on origin O. At a later time t’, Prime will see that the light has traveled a distance of ct’ and that the spherical wave is centered on origin O’ with a radius ct’. This is a profound statement! There is only one light sphere but both observers see the light sphere centered on their respective origins. This is very difficult to imagine. Figure 3 -3(b) attempts to show what the light sphere might look like in each frame. y y’ S S S’ S’ v v ct x x’ O O’ ct’ O O’ z z’ (a) Module 3 Special Relativity Fig. 3 -3 (b) 5

While the situation is difficult to imagine, the mathematics of the situation is straightforward. The surface of the light sphere in frame S must be (3. 11) Similarly, the surface of the sphere in frame S’ is (3. 12) We transform Eq. (3. 12) using Eqs. (3. 10) to get After squaring the sums in parentheses and collecting terms we can write (3. 13) Both Eq. (3. 13) and Eq. (3. 11) must be true so, by direct comparison of the coefficients in both equations, we must have (3. 14) We have three equations and three unknowns! We can solve for the last three elements. You will finish the algebra in a homework problem and show that Module 3 Special Relativity 6

(3. 15) Let us define to be a function of relative speed such that (3. 15) then it follows from Eq. (3. 10) that the transformation equations are (3. 16) We have done it. Here are the Lorentz transformation equations which describe the special theory of relativity. We said in the beginning of this module that these new equations are generalizations of the Galilean transformation equations. We see that this is indeed the case. If the relative speed between observers is such that v << c then the value of is approximately one, vx / c 2 is miniscule, and the Lorentz transformation equations become the Galilean transformation equations! Newtonian relativity is the special “low speed” case of special relativity. Module 3 Special Relativity 7

The New Space-time Four-vector Since we know all of the aij values, we can write the operator A as (3. 17) Notice that this matrix is symmetric along its diagonal. That is, element aij is equal to element aji. The transpose of a matrix is found by replacing element aij with aji. Thus, the transpose of a symmetric matrix is equal to itself. We can represent this for our matrix by writing A = AT where AT is the transpose of A. We could leave things like this and move on but we make one small change. Notice that two of the components of the space -time four-vector tau are now changed by A (the x and ct components). In the Glailean transformation equations, only one component was changed (the x component). However, the length of the tau and tau prime vectors are still different under the new transformation. You can show this by taking the square of the length of tau prime, transforming it, and comparing the result to the square of the lenth of tau. If you do this (and you will in a homework problem), you will find Is there a way to define the space-time four-vectors so that their lengths are the same and they work properly with the transformation equations? The answer is yes and Eqs. (3. 11) and (3. 12) supply the needed help. We know that these two equations must be satisfied simultaneously. Thus, we know that (3. 18) Module 3 Special Relativity 8

So we need a minus sign to appear in front of the square of the temporal component when we find the length of the fourvector. If we can do this, the lengths of the two vectors are equal. Can we do this? Yes! All we need to do is to write the temporal components as ict and ict’. When we square these components we get –c 2 t 2 and –c 2 t 2. We, therefore, define the new space-time four-vectors as (3. 19) Now we do have to update our operator A so that the new four-vectors satisfy the Lorentz transformation equations. We just have to modify two of the corner elements of the matrix. Let’s call this new operator L for Lorentz. In matrix form (3. 20) The Lorentz transformation of the space-time vectors can be succinctly written as (3. 21) With these new definitions for the four-vectors and the operator L we can state that the Lorentz transformation does rotate the space-time four-vector but it does not change its length. The length of the four-vector is invariant in special relativity. In subsequent modules, we will define other four-vectors that also possess this invariance in magnitude. One last observation is made before we end this module. Notice that matrix L is equal to the complex conjugate of its transpose. (To take the complex conjugate of a matrix you simply take the complex conjugate of each element. ) We can write this as L = (LT)* where the * means complex conjugate. A matrix that has this property is called Hermitian. Module 3 Special Relativity 9