Module 22 Graphs Graph Trees Chapters 10 11

Module #22 - Graphs Graph & Trees Chapters 10 -11 Acknowledgement This is a modified version of Module#22 on Graph Theory by Michael Frank Sultan Almuhammadi ICS 254: Graphs and Trees Spring 2020

Module #22 - Graphs What are Graphs? Not • General meaning in everyday math: A plot or chart of numerical data using a coordinate system. • Technical meaning in discrete mathematics: A particular class of discrete structures (to be defined) that is useful for representing relations and has a convenient webbylooking graphical representation. Sultan Almuhammadi ICS 254: Graphs and Trees 2

Module #22 - Graphs Applications of Graphs • Potentially anything (graphs can represent relations, relations can describe the extension of any predicate). • Apps in networking, scheduling, flow optimization, circuit design, path planning. • More apps: Geneology analysis, computer game-playing, program compilation, objectoriented design, … Sultan Almuhammadi ICS 254: Graphs and Trees 3

Module #22 - Graphs § 10. 1: Definition of Graph • A graph G = (V, E) – V is a nonempty set of verticies – E is a set of edges (arcs or links) between vertices – Type of edges: • Directed: ordered pairs (u, v) of vertices • Undirected: unordered pairs {u, v} of vertices Sultan Almuhammadi ICS 254: Graphs and Trees 4

Module #22 - Graphs Simple Graphs A simple graph G=(V, E) consists of: Visual Representation of a Simple Graph – a set V of vertices or nodes (V corresponds to the universe of the relation R), – a set E of edges: unordered pairs of [distinct] vertices u, v V Sultan Almuhammadi ICS 254: Graphs and Trees 5

Module #22 - Graphs Example of a Simple Graph • Let V be the set of the 6 GCC states: –V={KSA, UAE, KWT, OMN, QTR, BAH} • Let E={{u, v}| u adjoins v} E ={{KSA, UAE}, {KSA, KWT}, {KSA, BAH}, {KSA, QTR}, {UAE, OMN}} Sultan Almuhammadi ICS 254: Graphs and Trees 6

Module #22 - Graphs Multigraphs • Like simple graphs, but there may be more than one edge connecting two given nodes. • E. g. , nodes are cities, edges are segments of major highways between the cities. Parallel edges Sultan Almuhammadi ICS 254: Graphs and Trees 7

Module #22 - Graphs Pseudographs • Like a multigraph, but edges connecting a node to itself are allowed. (R may be reflexive. ) • A pseudograph G=(V, E) where Edge e E is a loop if loops e = {u, u} = {u}. • E. g. , nodes are the cities in a state, edges are the roads serving/connecting the cities. Sultan Almuhammadi ICS 254: Graphs and Trees 8

Module #22 - Graphs Directed Graphs • Correspond to arbitrary binary relations R, which may not be symmetric. • A directed graph (V, E) consists of a set of vertices V and a binary relation E on V. • E. g. : V = set of People, E={(x, y) | x loves y} Sultan Almuhammadi ICS 254: Graphs and Trees 9

Module #22 - Graphs Directed Multigraphs • Like directed graphs, but there may be more than one arc from a node to another. • E. g. , V=web pages, E=hyperlinks. The WWW is a directed multigraph. . . Sultan Almuhammadi ICS 254: Graphs and Trees 10

Module #22 - Graphs Types of Graphs: Summary • Summary of the book’s definitions. • Keep in mind this terminology is not fully standardized across different authors. . . Sultan Almuhammadi ICS 254: Graphs and Trees 11

Module #22 - Graphs § 10. 2: Graph Terminology You need to learn the following terms: • Adjacent, connects, endpoints, degree, initial, terminal, in-degree, out-degree, complete, cycles, wheels, n-cubes, bipartite, subgraph, union. Sultan Almuhammadi ICS 254: Graphs and Trees 12

Module #22 - Graphs Adjacency Let G be an undirected graph with edge set E. Let e E be (or map to) the pair {u, v}. Then we say: • u, v are adjacent / neighbors / connected. • Edge e is incident with vertices u and v. • Edge e connects u and v. • Vertices u and v are endpoints of edge e. Sultan Almuhammadi ICS 254: Graphs and Trees 13

Module #22 - Graphs Degree of a Vertex • Let G be an undirected graph, v V a vertex. • The degree of v, deg(v), is its number of incident edges. (Except that any self-loops are counted twice. ) • A vertex with degree 0 is called isolated. • A vertex of degree 1 is called pendant. Sultan Almuhammadi ICS 254: Graphs and Trees 14

Module #22 - Graphs Exercise • Find: – An element of degree 4 – An element of degree 3 – A pendant – An isolated vertix Sultan Almuhammadi ICS 254: Graphs and Trees 15

Module #22 - Graphs Handshaking Theorem • Let G be an undirected (simple, multi-, or pseudo-) graph with vertex set V and edge set E. Then • Corollary: Any undirected graph has an even number of vertices of odd degree. Sultan Almuhammadi ICS 254: Graphs and Trees 16

Module #22 - Graphs Directed Adjacency • Let G be a directed (possibly multi-) graph, and let e be an edge of G that is (or maps to) (u, v). Then we say: – u is adjacent to v, v is adjacent from u – e comes from u, e goes to v. – e connects u to v, e goes from u to v – the initial vertex of e is u – the terminal vertex of e is v Sultan Almuhammadi ICS 254: Graphs and Trees 17

Module #22 - Graphs Directed Degree • Let G be a directed graph, v a vertex of G. – The in-degree of v, deg (v), is the number of edges going to v. – The out-degree of v, deg (v), is the number of edges coming from v. – The degree of v, deg(v): deg (v)+deg (v), is the sum of v’s in-degree and out-degree. Sultan Almuhammadi ICS 254: Graphs and Trees 18

Module #22 - Graphs Directed Handshaking Theorem • Let G be a directed (possibly multi-) graph with vertex set V and edge set E. Then: • Note that the degree of a node is unchanged by whether we consider its edges to be directed or undirected. Sultan Almuhammadi ICS 254: Graphs and Trees 19

Module #22 - Graphs Special Graph Structures Special cases of undirected graph structures: • Complete graphs Kn • Cycles Cn • Wheels Wn • n-Cubes Qn • Bipartite graphs • Complete bipartite graphs Km, n Sultan Almuhammadi ICS 254: Graphs and Trees 20

Module #22 - Graphs Complete Graphs • For any n N, a complete graph on n vertices, Kn, is a simple graph with n nodes in which every node is adjacent to every other node: u, v V: u v {u, v} E. K 1 K 2 Note that Kn has Sultan Almuhammadi K 3 K 4 K 5 K 6 edges. ICS 254: Graphs and Trees 21

Module #22 - Graphs Cycles • For any n 3, a cycle on n vertices, Cn, is a simple graph where V={v 1, v 2, … , vn} and E={{v 1, v 2}, {v 2, v 3}, …, {vn 1, vn}, {vn, v 1}}. C 3 C 4 C 5 C 6 C 7 C 8 How many edges are there in Cn? Sultan Almuhammadi ICS 254: Graphs and Trees 22

Module #22 - Graphs Wheels • For any n 3, a wheel Wn, is a simple graph obtained by taking the cycle Cn and adding one extra vertex vhub and n extra edges {{vhub, v 1}, {vhub, v 2}, …, {vhub, vn}}. W 3 W 4 W 5 W 6 W 7 How many edges are there in Wn? Sultan Almuhammadi ICS 254: Graphs and Trees W 8 23

Module #22 - Graphs n-cubes (hypercubes) • For any n N, the hypercube Qn is a simple graph consisting of two copies of Qn-1 connected together at corresponding nodes. Q 0 has 1 node. Q 0 Q 1 Q 2 Q 3 Q 4 Number of vertices: 2 n. Number of edges: Exercise to try! Sultan Almuhammadi ICS 254: Graphs and Trees 24

Module #22 - Graphs Bipartite Graphs • Def’n. : A graph G=(V, E) is bipartite (twopart) iff V = V 1 V 2 where V 1 ∩ V 2= and e E: v 1 V 1, v 2 V 2: e={v 1, v 2}. • In English: The graph can be divided into two parts in such a way that all edges go between the two parts. This definition can easily be adapted for the case of multigraphs and directed graphs as well. Sultan Almuhammadi ICS 254: Graphs and Trees V 1 V 2 Can represent with zero-one matrices. 25

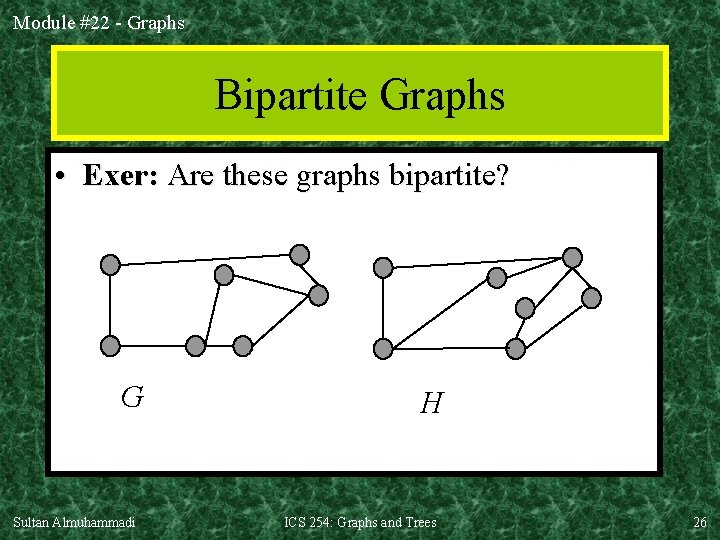
Module #22 - Graphs Bipartite Graphs • Exer: Are these graphs bipartite? G Sultan Almuhammadi H ICS 254: Graphs and Trees 26

Module #22 - Graphs Complete Bipartite Graphs • For m, n N, the complete bipartite graph Km, n is a bipartite graph where |V 1| = m, |V 2| = n, and E = {{v 1, v 2}|v 1 V 1 v 2 V 2}. – That is, there are m nodes K 4, 3 in the left part, n nodes in the right part, and every node in the left part is connected to every node Km, n has _____ nodes in the right part. and _____ edges. Sultan Almuhammadi ICS 254: Graphs and Trees 27

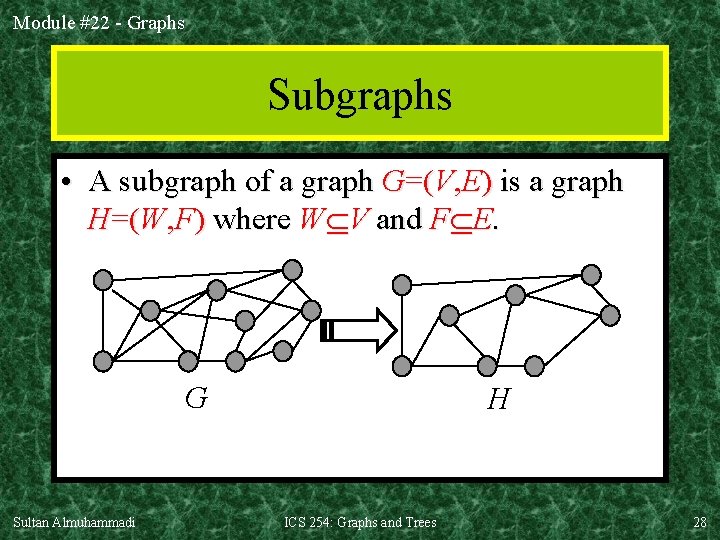
Module #22 - Graphs Subgraphs • A subgraph of a graph G=(V, E) is a graph H=(W, F) where W V and F E. G Sultan Almuhammadi H ICS 254: Graphs and Trees 28

Module #22 - Graphs Graph Unions • The union G 1 G 2 of two simple graphs G 1=(V 1, E 1) and G 2=(V 2, E 2) is the simple graph (V 1 V 2, E 1 E 2). Sultan Almuhammadi a b d e c a d ICS 254: Graphs and Trees b c f 29

Module #22 - Graphs § 10. 3: Graph Representations & Isomorphism • Graph representations: – Adjacency lists. – Adjacency matrices. – Incidence matrices. • Graph isomorphism: – Two graphs are isomorphic iff they are identical except for their node names. Sultan Almuhammadi ICS 254: Graphs and Trees 30

Module #22 - Graphs Adjacency Lists • A table with 1 row per vertex, listing its adjacent vertices. b a c d f Sultan Almuhammadi e ICS 254: Graphs and Trees 31

Module #22 - Graphs Directed Adjacency Lists • 1 row per node, listing the terminal nodes of each edge incident from that node. Sultan Almuhammadi ICS 254: Graphs and Trees 32

Module #22 - Graphs Adjacency Matrices • A way to represent simple graphs – possibly with self-loops. • Matrix A=[aij], where aij is 1 if {vi, vj} is an edge of G, and is 0 otherwise. • Can extend to pseudographs by letting each matrix elements be the number of links (possibly >1) between the nodes. Sultan Almuhammadi ICS 254: Graphs and Trees 33

Module #22 - Graphs Graph Isomorphism • Formal definition: – Simple graphs G 1=(V 1, E 1) and G 2=(V 2, E 2) are isomorphic iff a bijection f: V 1 V 2 such that a, b V 1, a and b are adjacent in G 1 iff f(a) and f(b) are adjacent in G 2. – f is the “renaming” function between the two node sets that makes the two graphs identical. – This definition can easily be extended to other types of graphs. Sultan Almuhammadi ICS 254: Graphs and Trees 34

Module #22 - Graphs Graph Invariants under Isomorphism Necessary but not sufficient conditions for G 1=(V 1, E 1) to be isomorphic to G 2=(V 2, E 2): – We must have that |V 1|=|V 2|, and |E 1|=|E 2|. – The number of vertices with degree n is the same in both graphs. – For every proper subgraph g of one graph, there is a proper subgraph of the other graph that is isomorphic to g. Sultan Almuhammadi ICS 254: Graphs and Trees 35

Module #22 - Graphs Isomorphism Example • If isomorphic, label the 2 nd graph to show the isomorphism, else identify difference. d b a d e Sultan Almuhammadi b c f c ICS 254: Graphs and Trees a f e 36

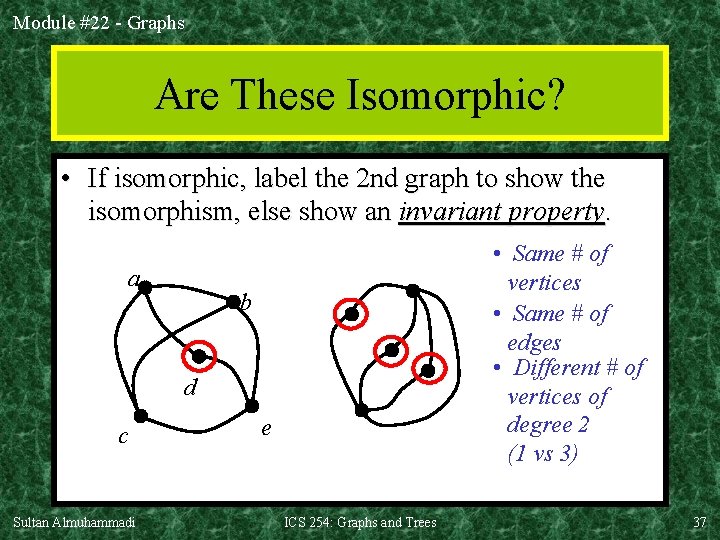
Module #22 - Graphs Are These Isomorphic? • If isomorphic, label the 2 nd graph to show the isomorphism, else show an invariant property. a • Same # of vertices • Same # of edges • Different # of vertices of degree 2 (1 vs 3) b d c Sultan Almuhammadi e ICS 254: Graphs and Trees 37

Module #22 - Graphs § 10. 4: Connectivity • A path, p, from u to v is a sequence of adjacent edges going from vertex u to vertex v. e. g. p = (u, x), (x, y), …, (z, v) • A path is a circuit if u=v. • A path traverses the vertices along it. • A path is simple if it contains no edge more than once. Sultan Almuhammadi ICS 254: Graphs and Trees 38

Module #22 - Graphs The length of the path • the length of the path p |p| = number of edges in p e. g. p = (a, b), (b, c), (c, d) |p| = 3 Sultan Almuhammadi ICS 254: Graphs and Trees 39

Module #22 - Graphs Connected Graphs • An undirected graph is connected iff there is a path between every pair of distinct vertices in the graph. Sultan Almuhammadi ICS 254: Graphs and Trees 40

Module #22 - Graphs Directed Connectedness • A directed graph is strongly connected iff there is a directed path from a to b for any two vertices a and b. • It is weakly connected iff the underlying undirected graph (i. e. , with edge directions removed) is connected. • Note strongly implies weakly but not viceversa. Sultan Almuhammadi ICS 254: Graphs and Trees 41

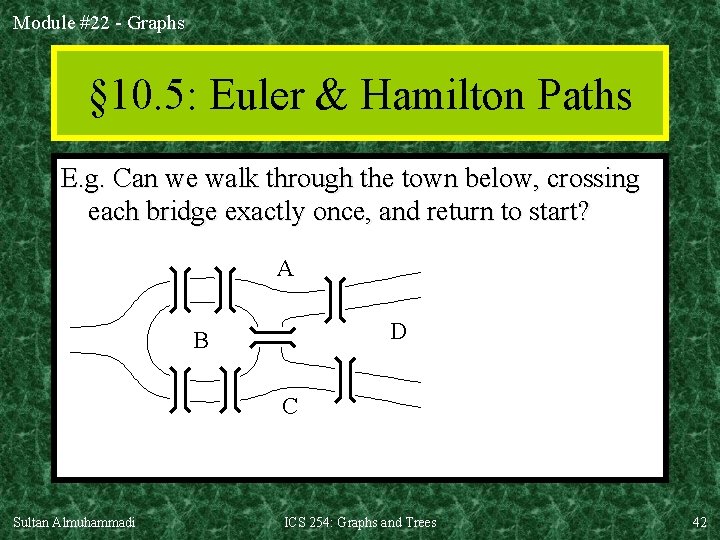
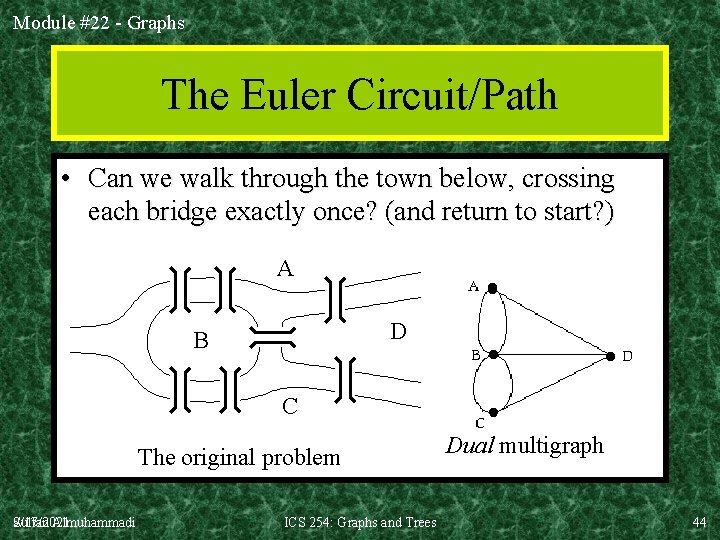
Module #22 - Graphs § 10. 5: Euler & Hamilton Paths E. g. Can we walk through the town below, crossing each bridge exactly once, and return to start? A D B C Sultan Almuhammadi ICS 254: Graphs and Trees 42

Module #22 - Graphs § 10. 5: Euler & Hamilton Paths • Euler circuit: a simple circuit containing every edge (exactly once) • Euler path: in G is a simple path containing every edge (exactly once) 9/17/2021 Sultan Almuhammadi ICS 254: Graphs and Trees 43

Module #22 - Graphs The Euler Circuit/Path • Can we walk through the town below, crossing each bridge exactly once? (and return to start? ) A D B C The original problem 9/17/2021 Sultan Almuhammadi ICS 254: Graphs and Trees Dual multigraph 44

Module #22 - Graphs The Euler Circuit/Path • Exer: Does K 4 have an EC? EP? Does K 5 have an EC? EP? 9/17/2021 Sultan Almuhammadi ICS 254: Graphs and Trees 45

Module #22 - Graphs Euler Path Theorems • Thrm 1: A connected multigraph has an Euler circuit iff each vertex has even degree. • Thrm 2: A connected multigraph has an Euler path (but not an Euler circuit) iff it has exactly 2 vertices of odd degree. – One is the start, the other is the end. Sultan Almuhammadi ICS 254: Graphs and Trees 46

Module #22 - Graphs § 10. 5: Euler & Hamilton Paths • A Hamilton circuit is a circuit that traverses each vertex in G exactly once. • A Hamilton path is a path that traverses each vertex in G exactly once. • E. g. Does W 5 have an HC? HP? 9/17/2021 Sultan Almuhammadi ICS 254: Graphs and Trees 47

Module #22 - Graphs § 10. 7: Planar Graphs • Defn. G is planar if it can be drawn on the plane without crossing edges. • Eg. K 3, K 4, Q 2 • Exer: Is K 3, 3 planar? • Exer: Is K 5 planar? Sultan Almuhammadi ICS 254: Graphs and Trees 48

Module #22 - Graphs § 10. 7: Planar Graphs • Planar representation of a graph makes regions. R 1 R 2 R 3 R 4 R 5 v = 8, e =11, r = 5 • Euler Formula: r=e–v+2 Sultan Almuhammadi ICS 254: Graphs and Trees 49

Module #22 - Graphs § 10. 8: Graph Coloring • Coloring of a simple graph G=(V, E) is a mapping f: V A, where A = {1, 2, . . , n} is a set of colors, such that for every edge (x, y) in E, f(x) ≠ f(y) i. e. Adjacent vertices have different colors G: Sultan Almuhammadi ICS 254: Graphs and Trees 50

Module #22 - Graphs § 10. 8: Graph Coloring • The chromatic number of G, denoted by χ(G), is the minimum number of colors G can have. • E. g. Find χ(G). G: Sultan Almuhammadi ICS 254: Graphs and Trees 51

Module #22 - Graphs Graph Coloring Example • E. g. Find χ(W 5) 9/17/2021 Sultan Almuhammadi ICS 254: Graphs and Trees 52

Module #22 - Graphs Exer: Graph Coloring • Exer: Find χ(G) where G is: • W 8 • K 5, 3 9/17/2021 Sultan Almuhammadi ICS 254: Graphs and Trees 53

Module #22 - Graphs Graph Coloring • Theorems on χ(G): – If G is bipartite, then χ(G) ≤ 2 – If G is a plannar graph, then χ(G) ≤ 4 (Map coloring of the dual graph*) 9/17/2021 Sultan Almuhammadi ICS 254: Graphs and Trees 54

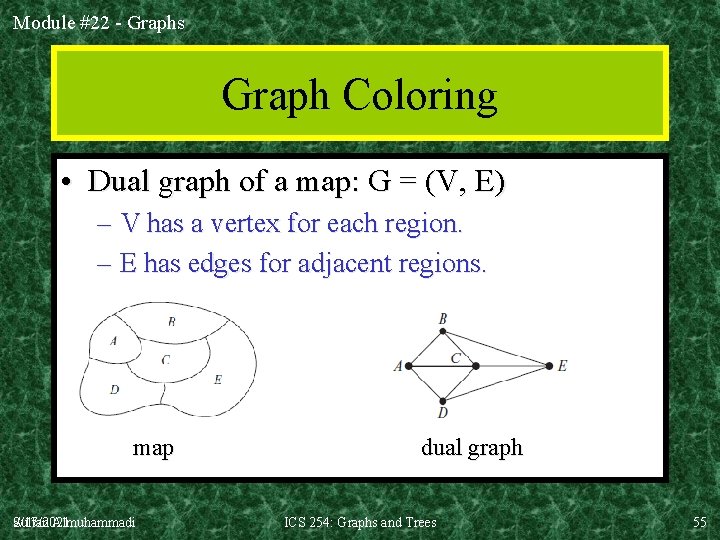
Module #22 - Graphs Graph Coloring • Dual graph of a map: G = (V, E) – V has a vertex for each region. – E has edges for adjacent regions. map 9/17/2021 Sultan Almuhammadi dual graph ICS 254: Graphs and Trees 55

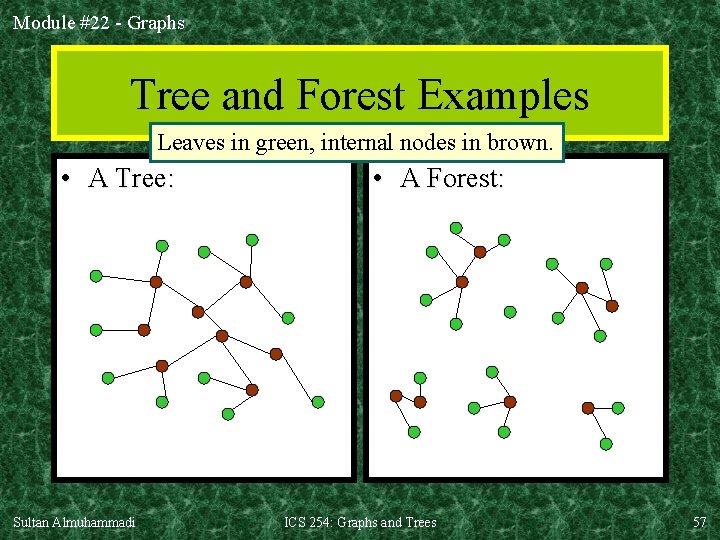
Module #22 - Graphs § 11. 1: Introduction to Trees • A tree is a connected undirected graph that contains no circuits. • Thrm 1: There is a unique simple path between any two of its nodes. • Thrm 2: T=(V, E) is a tree iff |E| = |V| - 1 • A (not-necessarily-connected) undirected graph without simple circuits is called a forest. – A forest is a bunch of trees Sultan Almuhammadi ICS 254: Graphs and Trees 56

Module #22 - Graphs Tree and Forest Examples Leaves in green, internal nodes in brown. • A Tree: Sultan Almuhammadi • A Forest: ICS 254: Graphs and Trees 57

Module #22 - Graphs Rooted Trees • A rooted tree is a tree in which one node has been designated the root. – Every edge is directed away from the root. • Keywords about rooted trees: – Parent, child, siblings, ancestors, descendents, leaf, internal node, subtree. Sultan Almuhammadi ICS 254: Graphs and Trees 58

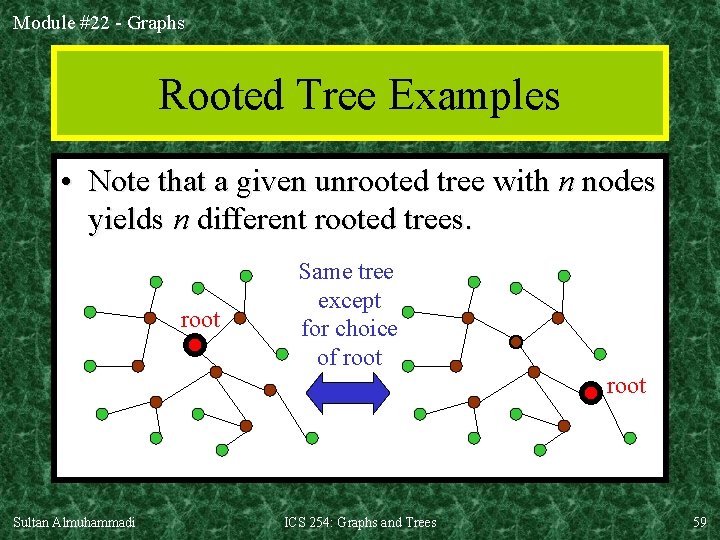
Module #22 - Graphs Rooted Tree Examples • Note that a given unrooted tree with n nodes yields n different rooted trees. root Same tree except for choice of root Sultan Almuhammadi ICS 254: Graphs and Trees 59

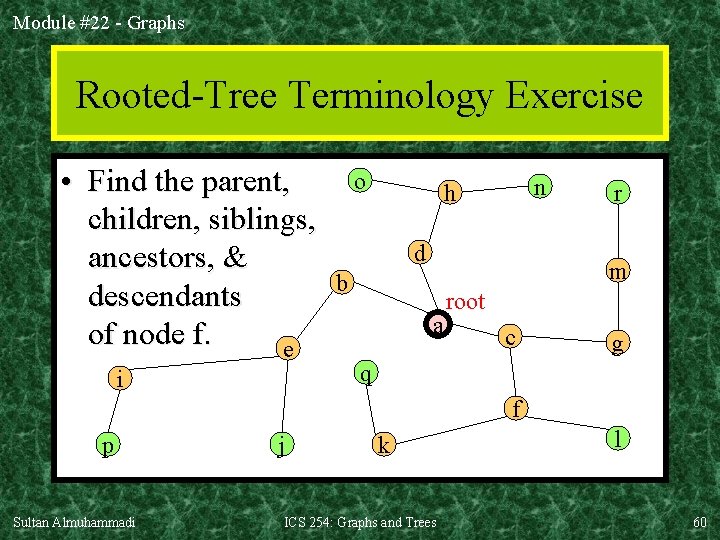
Module #22 - Graphs Rooted-Tree Terminology Exercise • Find the parent, children, siblings, ancestors, & descendants of node f. e i o n h d r m b a root c g q f p Sultan Almuhammadi j k ICS 254: Graphs and Trees l 60

Module #22 - Graphs n-ary trees • A rooted tree is called n-ary if every vertex has no more than n children. e. g. binary tree for n = 2 Sultan Almuhammadi ICS 254: Graphs and Trees 61

Module #22 - Graphs Rooted-Tree Terminology • Definition: The level of a node is the length of the simple path from the root to the node. – The height of a tree is maximum node level. Sultan Almuhammadi ICS 254: Graphs and Trees 62

Module #22 - Graphs § 11. 3: Tree Traversal • Preorder traversal – Root, then subtrees (left-to-right) • Inorder traversal – Left subtree, root, then other subtrees • Postorder traversal – Subtrees (left-to-right) before the root. Sultan Almuhammadi ICS 254: Graphs and Trees 63

Module #22 - Graphs Infix/prefix/postfix notation E. g. Draw the rooted tree for: (x + y) / (x^2) • Infix form: (x+y) / (x^2) – (need parentheses) • Prefix form (polish notation): /+xy^x 2 • Postfix form (reverse polish notation): xy+x 2^/ 9/17/2021 Sultan Almuhammadi ICS 254: Graphs and Trees 64