Module 2 Topic B Lesson 4 Metric Unit

Module 2 Topic B Lesson 4 Metric Unit Conversions 4. MD. 1 and 4. MD. 2

Lesson 4 Objective • Know and relate metric units to place value units in order to express measurements in different units

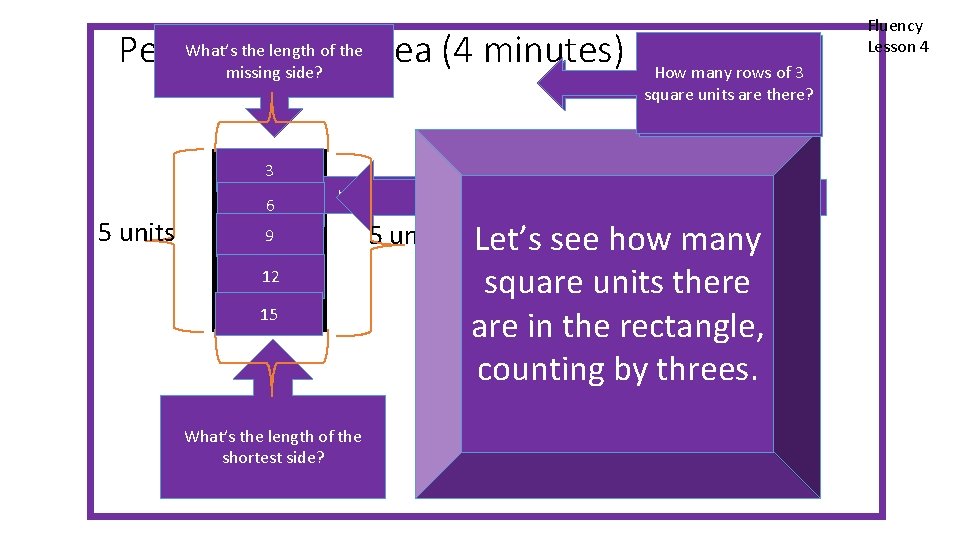
What’s 3 theunits length of the. Area (4 minutes) Perimeter and missing side? 5 3 How square units How many of 3 manyrows square units are in are onethere? row? 3 5 units 6 What’s the length of the What’s thelongest lengthside? of the opposite side? 9 12 15 3 units What’s the length of the shortest side? 5 units Let’s see how many 106 Units square units there What is the sum of the rectangle’s twoshortest longest are in the rectangle, lengths? counting by threes. Fluency Lesson 4

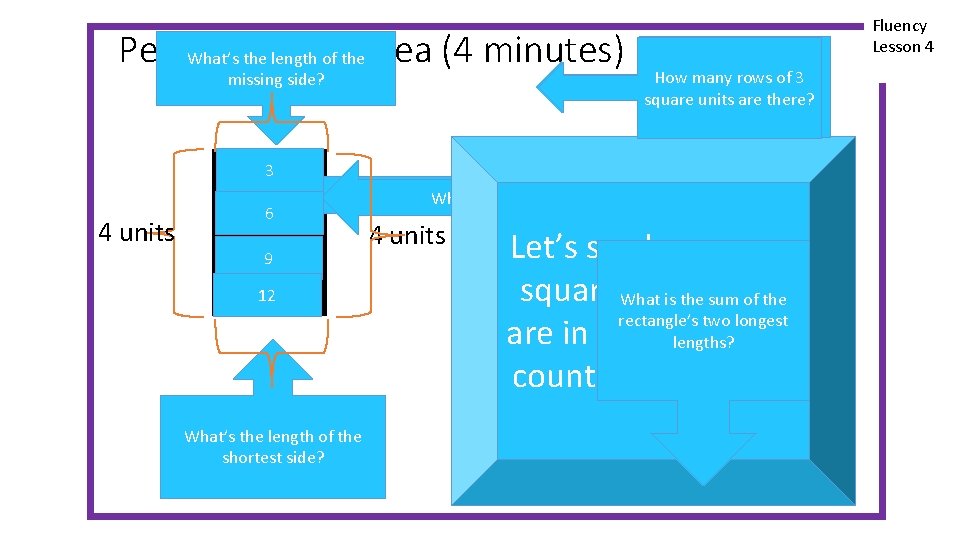
Perimeter and What’s 3 theunits length of the. Area (4 minutes) missing side? 34 square units Howmanysquare rows ofunits 3 areunits in one square arerow? there? 3 4 units 6 What’s the length ofthe thelength longestofside? What’s the opposite side? 9 12 3 units What’s the length of the shortest side? 4 units Let’s see how many 6 Units 8 square. What units What is the there sum of of the is sum rectangle’stwo twoshortest longest rectangle’s are in the rectangle, lengths? counting by threes. Fluency Lesson 4

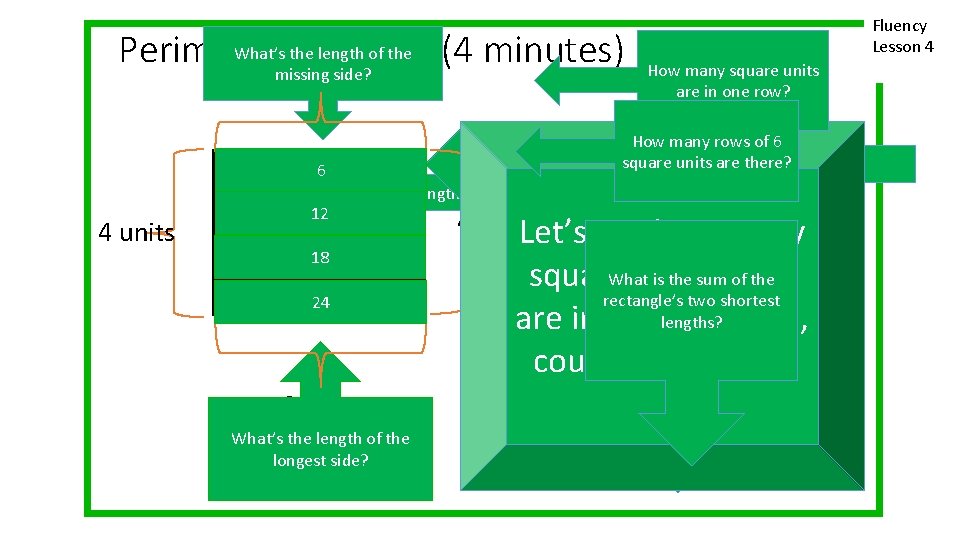
units What’s 6 and the length. Area of the Perimeter (4 minutes) missing side? How many rows of 6 squareof units there? side? What’s the length the are opposite 6 4 units 12 square units 64 square units How many square units are in one row? What’s the length of the shortest side? 18 24 6 units What’s the length of the longest side? 4 units Let’s see how many What is. Units the sum of the square units there 8 Units 12 rectangle’s two of shortest What is the sum the are inrectangle’s the lengths? rectangle, two longest lengths? counting by sixes. Fluency Lesson 4

Fluency Practice – Sprint A Take your mark! Get set! Think!

Get set! Fluency Practice – Sprint B Take your mark! There is a mistake in the module - they have no sprint B. Perhaps they will correct this error in later versions of the module. Think!

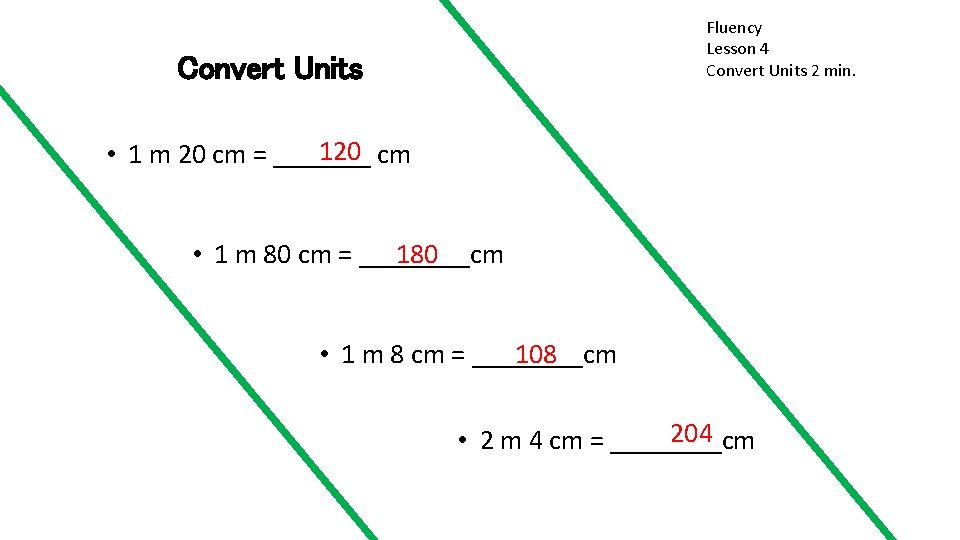
Fluency Lesson 4 Convert Units 2 min. Convert Units 120 cm • 1 m 20 cm = _______ 180 • 1 m 80 cm = ____cm • 1 m 8 cm = ____cm 108 204 • 2 m 4 cm = ____cm

Fluency Lesson 4 Convert Units 2 min. Convert Units 1 ___g 500 • 1, 500 g = ____kg 1 ____g 300 • 1, 300 g = ____kg • 1, 030 g = ____kg 1 ____g 30 1 ____g 5 • 1, 005 g = ____kg

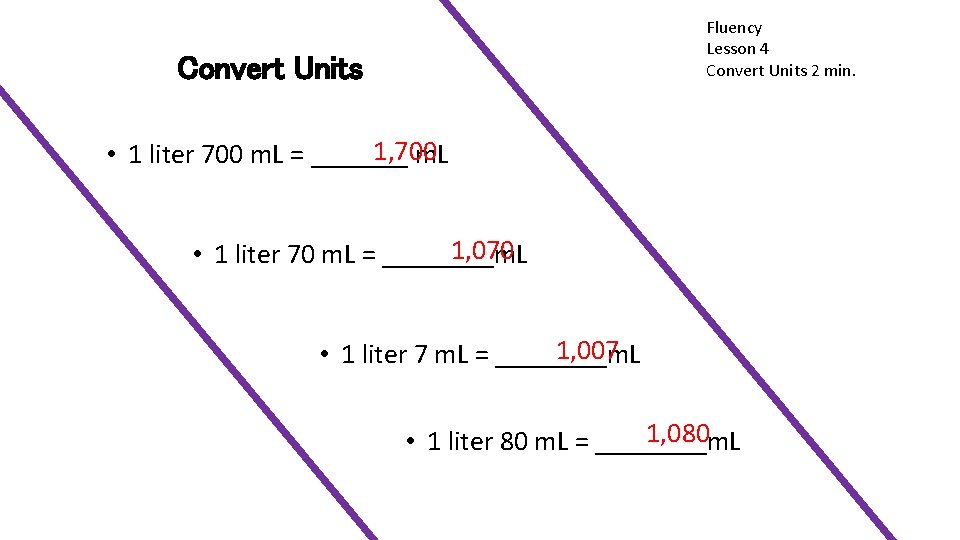
Fluency Lesson 4 Convert Units 2 min. Convert Units 1, 700 • 1 liter 700 m. L = _______ m. L 1, 070 • 1 liter 70 m. L = ____m. L 1, 007 • 1 liter 7 m. L = ____m. L 1, 080 • 1 liter 80 m. L = ____m. L

Fluency Lesson 4 Unit counting (4 minutes) • Count by 500 m. L in the following sequence and change directions when you see the arrow. • • • 500 m. L 1, 000 m. L 1, 500 m. L 2, 000 m. L 2, 500 m. L 3, 000 m. L • • • 2, 500 m. L 2, 000 m. L 1, 500 m. L 1, 000 m. L 500 m. L You did it!

Fluency Lesson 4 Unit counting (4 minutes) • Count by 500 m. L in the following sequence and change directions when you see the arrow. • • • 500 m. L 1 liter 1, 500 m. L 2 liters 2, 500 m. L 3 liters • • • 2, 500 m. L 2 liters 1, 500 m. L 1 liter 500 m. L 0 liters You did it!

Fluency Lesson 4 Unit counting (4 minutes) • Count by 200 m. L in the following sequence. You will not change directions this time. • • 200 m. L 400 m. L 600 m. L 800 m. L 1 liter 200 m. L 1 liter 400 m. L • • 1 liter 600 m. L 1 liter 800 m. L 2 liters 200 m. L 2 liters 400 m. L 2 liters 600 m. L 2 liters 800 m. L 3 liters You did it!

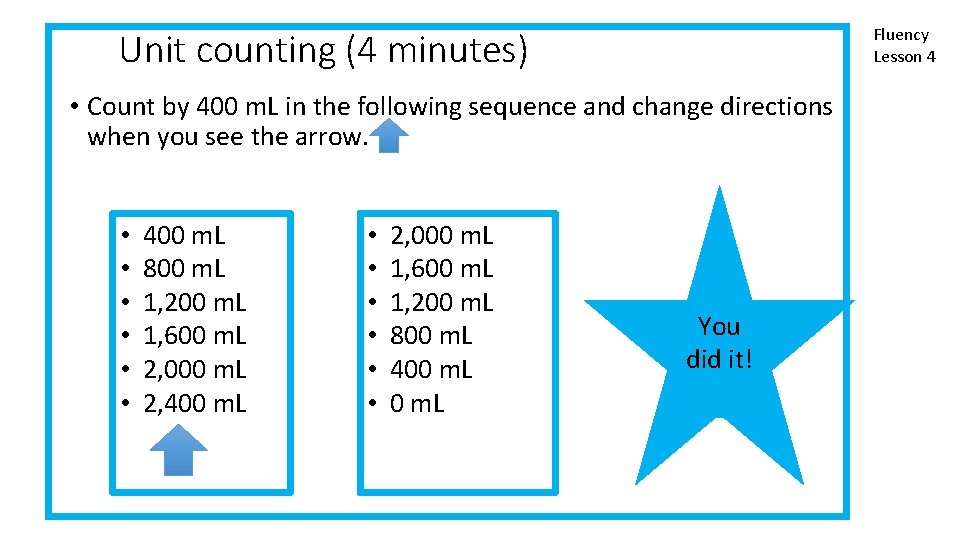
Fluency Lesson 4 Unit counting (4 minutes) • Count by 400 m. L in the following sequence and change directions when you see the arrow. • • • 400 m. L 800 m. L 1, 200 m. L 1, 600 m. L 2, 000 m. L 2, 400 m. L • • • 2, 000 m. L 1, 600 m. L 1, 200 m. L 800 m. L 400 m. L You did it!

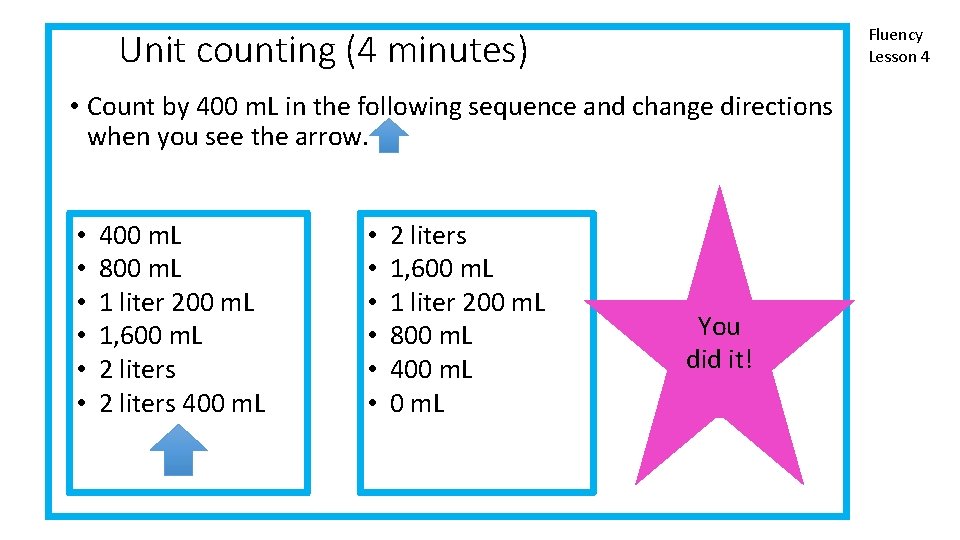
Fluency Lesson 4 Unit counting (4 minutes) • Count by 400 m. L in the following sequence and change directions when you see the arrow. • • • 400 m. L 800 m. L 1 liter 200 m. L 1, 600 m. L 2 liters 400 m. L • • • 2 liters 1, 600 m. L 1 liter 200 m. L 800 m. L 400 m. L You did it!

Application Problem Adam poured 1 liter 460 milliliters of water into a beaker. Over three days, some of the water evaporated. On day four, 979 milliliters of water remained in the beaker. How much water evaporated? Application Problem Lesson 4

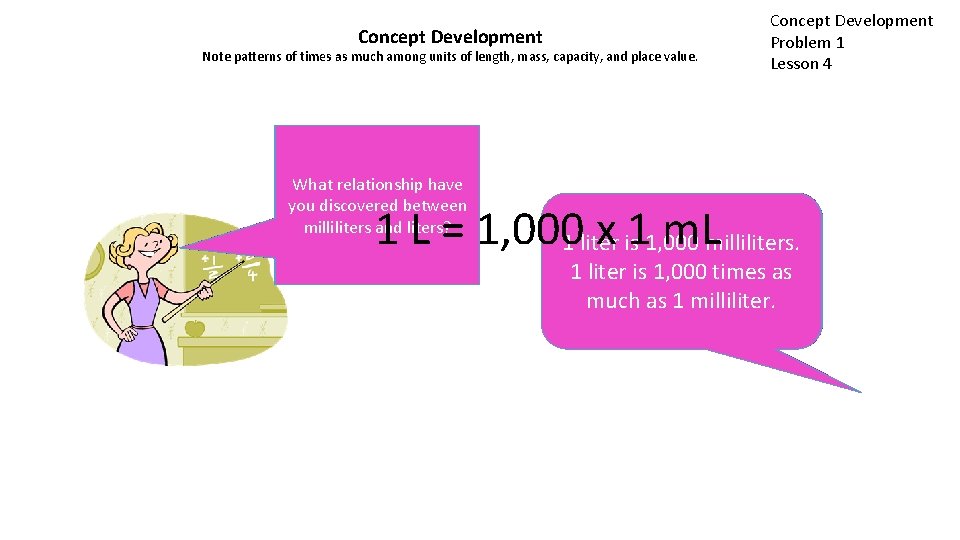
Concept Development Note patterns of times as much among units of length, mass, capacity, and place value. Turn and tell your What neighbor relationship the unitshave for youmass, discovered length, between and capacity milliliters that andwe liters? have learned so far. Concept Development Problem 1 Lesson 4 1 L = 1, 0001 literx. Gram, 11, 000 m. L is kilogram, milliliters. 1 liter centimeter, is 1, 000 meter, times as kilometer, much asmilliliter, 1 milliliter.

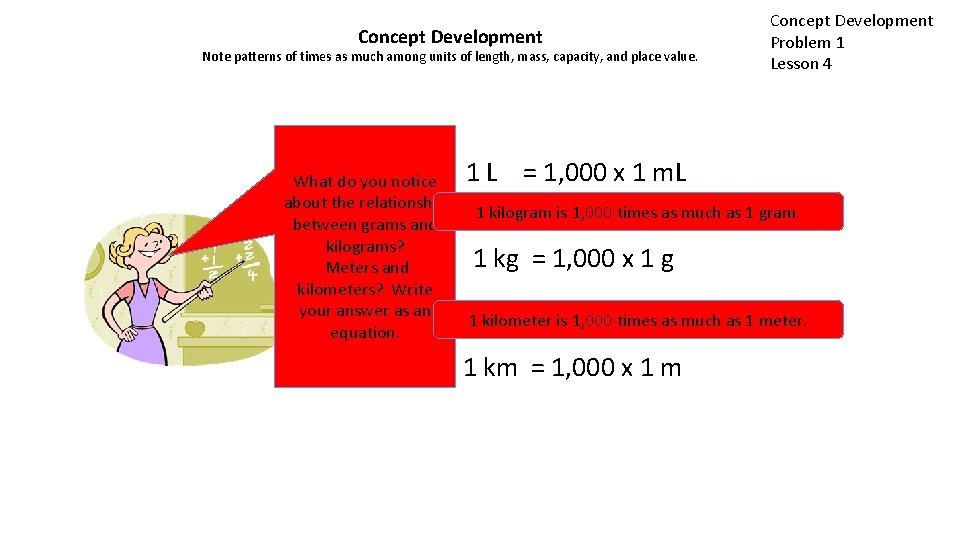
Concept Development Note patterns of times as much among units of length, mass, capacity, and place value. What do you notice about the relationship between grams and kilograms? Meters and kilometers? Write your answer as an equation. Concept Development Problem 1 Lesson 4 1 L = 1, 000 x 1 m. L 1 kilogram is 1, 000 times as much as 1 gram. 1 kg = 1, 000 x 1 g 1 kilometer is 1, 000 times as much as 1 meter. 1 km = 1, 000 x 1 m

Concept Development Note patterns of times as much among units of length, mass, capacity, and place value. Concept Development Problem 1 Lesson 4 I wonder if other units have similar relationships. What other units have we discussed in fourth grade so far? Ones Ten thousands Tens Hundred thousands Thousands

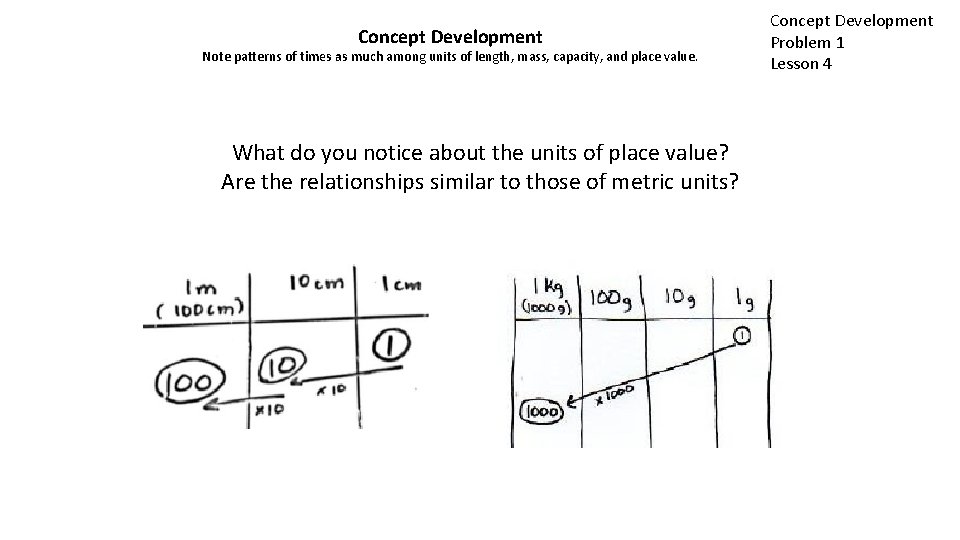
Concept Development Note patterns of times as much among units of length, mass, capacity, and place value. What do you notice about the units of place value? Are the relationships similar to those of metric units? Concept Development Problem 1 Lesson 4

Concept Development Note patterns of times as much among units of length, mass, capacity, and place value. Concept Development Problem 1 Lesson 4 unit is 100 times as much as 1 centimeter? 1 What hundred is 100 times Write your answer as an equation. as much as 1 one. 1 meter = 100 x 1 centimeter Can you think of a place value unit relation that is similar? 1 hundred thousand is 100 times as much as 1 thousand.

Concept Development Relate units of length, mass, and capacity to units of place value • • • 1 m = 100 cm One meter is 100 centimeters. What unit is 100 ones? 1 hundred = 100 ones 1 thousand = 1, 000 ones 1, 200 m. L = 1 liter 200 m. L 1, 200 = 1 thousand 200 ones 15, 450 m. L = 15 liters 450 m. L 15, 450 ones = 15 thousand 450 ones 15, 450 kilograms = 15 kilograms 450 grams 895 cm = 8 meters 95 cm 895 ones = 8 hundreds 95 ones Concept Development Problem 2 Lesson 4

Concept Development Problem 2 Lesson 4 Concept Development Relate units of length, mass, and capacity to units of place value 1 L 1, 200 m. L = 1 liter 200 m. L 1, 000 10 m. L 100 100 How are the two charts similar? 1, 200 = 1 thousand 200 ones 1 , 2 Thousands Hundreds 1, 000 100 0 Tens 0 Ones 100 1 , 2 0 0

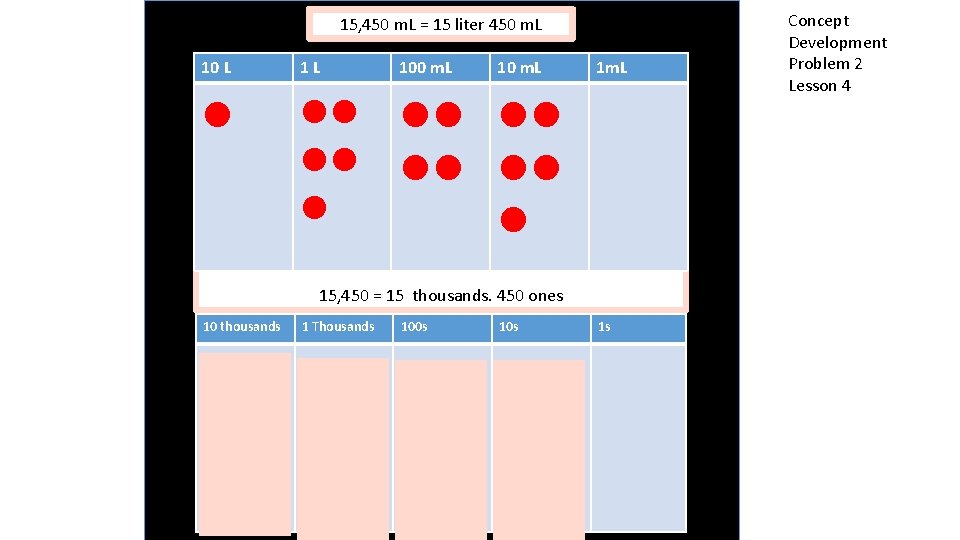
15, 450 m. L = 15 liter 450 m. L 10 L 1 L 100 m. L 10 m. L l ll ll ll l l 1 m. L 15, 450 = 15 thousands. 450 ones 10 thousands 1 Thousands 100 s 10 s l ll ll ll l l 1 s Concept Development Problem 2 Lesson 4

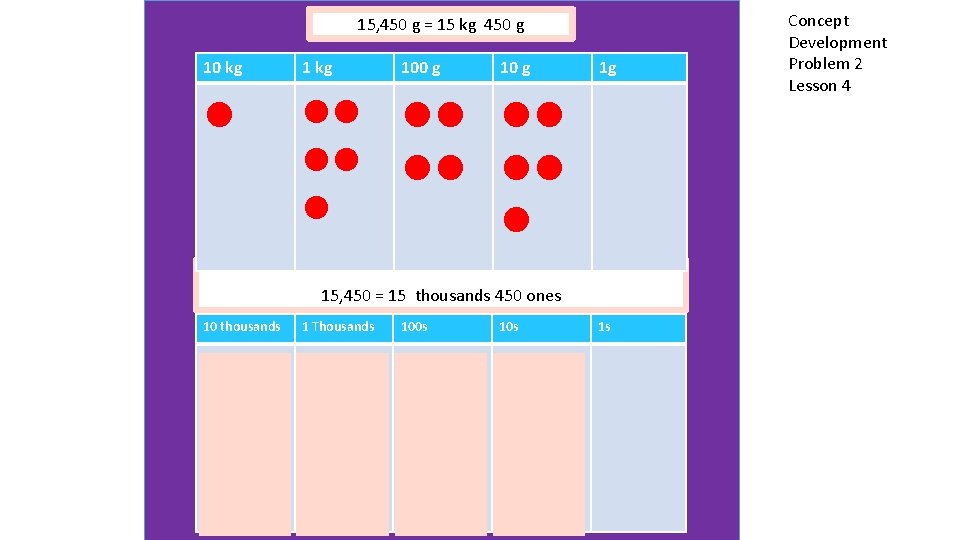
15, 450 g = 15 kg 450 g 10 kg 100 g 10 g l ll ll ll l l 1 g 15, 450 = 15 thousands 450 ones 10 thousands 1 Thousands 100 s 10 s l ll ll ll l l 1 s Concept Development Problem 2 Lesson 4

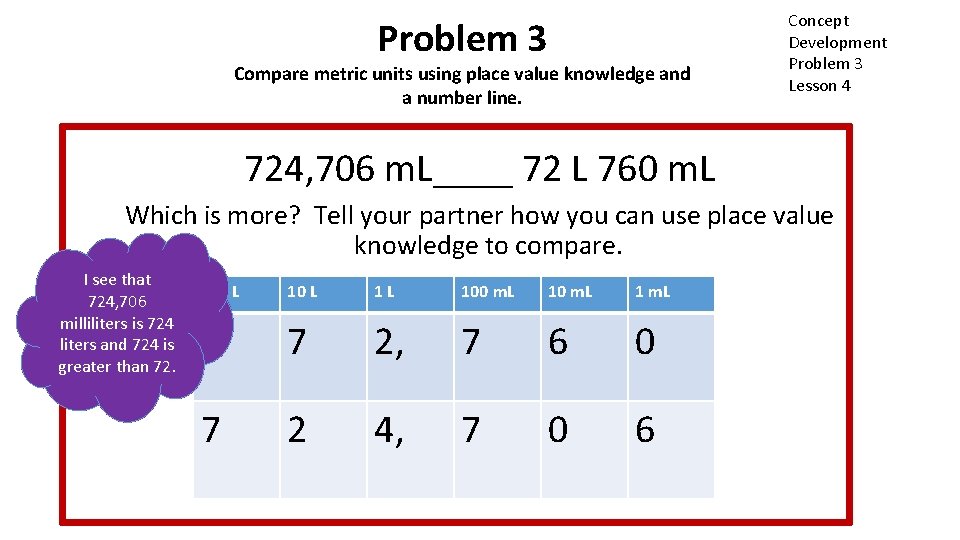
Problem 3 Compare metric units using place value knowledge and a number line. Concept Development Problem 3 Lesson 4 724, 706 m. L____ 72 L 760 m. L Which is more? Tell your partner how you can use place value knowledge to compare. I see that 724, 706 milliliters is 724 liters and 724 is greater than 72. 100 L 7 10 L 1 L 100 m. L 1 m. L 7 2, 7 6 0 2 4, 7 0 6

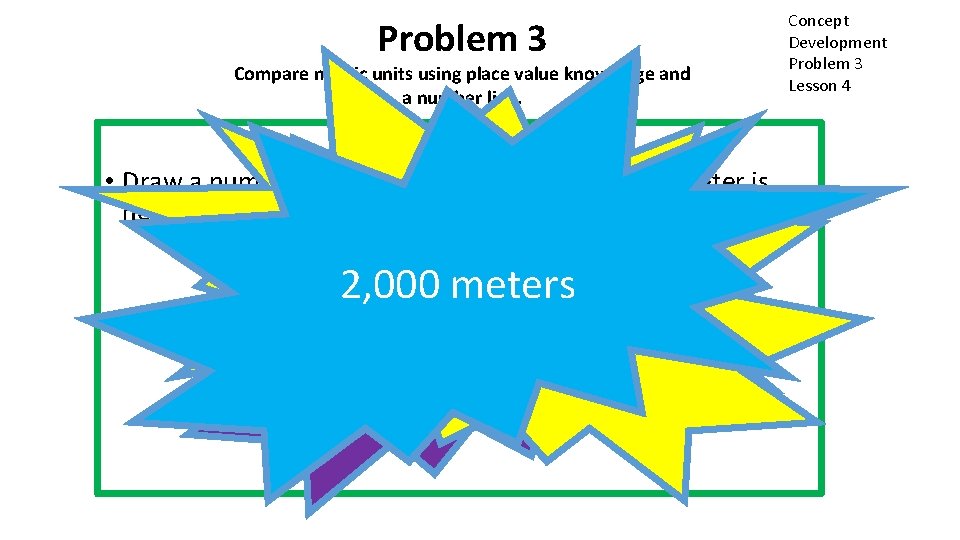
Problem 3 Compare metric units using place value knowledge and a number line. • Draw a number line from 0 km to 2 km. One kilometer is how many meters? 2 kilometers is equal 2, 000 meters to meters how 1, 000 many meters? Concept Development Problem 3 Lesson 4

Problem 3 Compare metric units using place value knowledge and a number line. Concept Development Problem 3 Lesson 4 • Discuss with your partner how many centimeters are equal to 1 kilometer. • 1 meter is 100 centimeters. • 1 kilometer is 1 thousand meters. • So, 1 thousand times 1 hundred is easy, it is 100 thousand. • 2 meters is 200 centimeters so 10 meters is 1, 000 centimeters. • Ten of those is 100, 000 centimeters.

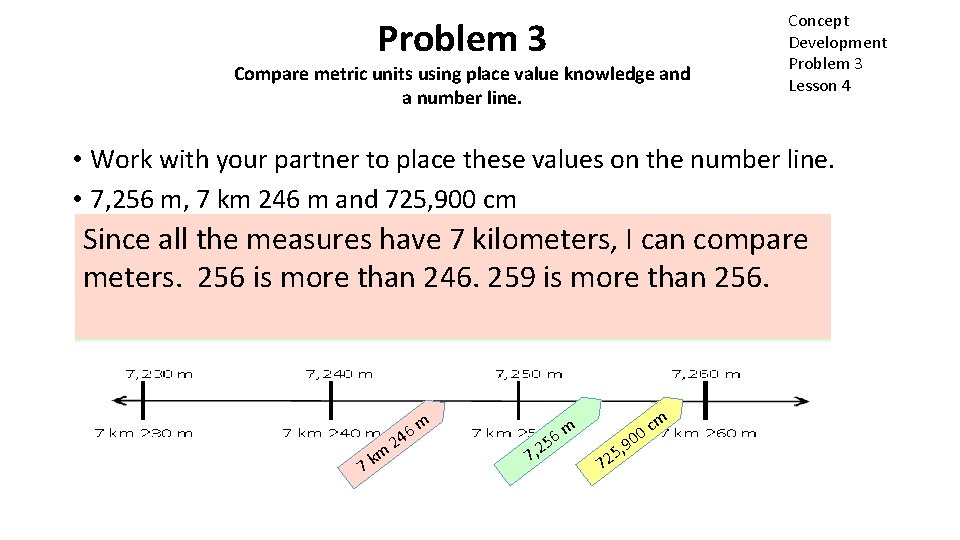
Problem 3 Compare metric units using place value knowledge and a number line. Concept Development Problem 3 Lesson 4 • Work with your partner to place these values on the number line. • 7, 256 m, 7 km 246 m and 725, 900 cm Since measures havem 7 and kilometers, 7, 256 all m the is between 7, 250 7, 260 m. I can It iscompare less that meters. more 246. 259 is more than 256. m) 7, 259 m. 256 7 kmis 246 mthan is between 7 km 240 m (7, 240 and 7 km 250 m (7, 250 m ). I know that 100 cm equals 1 meter. In the number 725, 900 there are 7, 259 hundreds. That means that 725, 900 cm = 7, 259 m. Now I am able to place 725, 900 cm on the number line. 7 km 2 m 46 7 m 6 , 25 m 72 c 0 0 5, 9

Problem Set (10 Minutes)

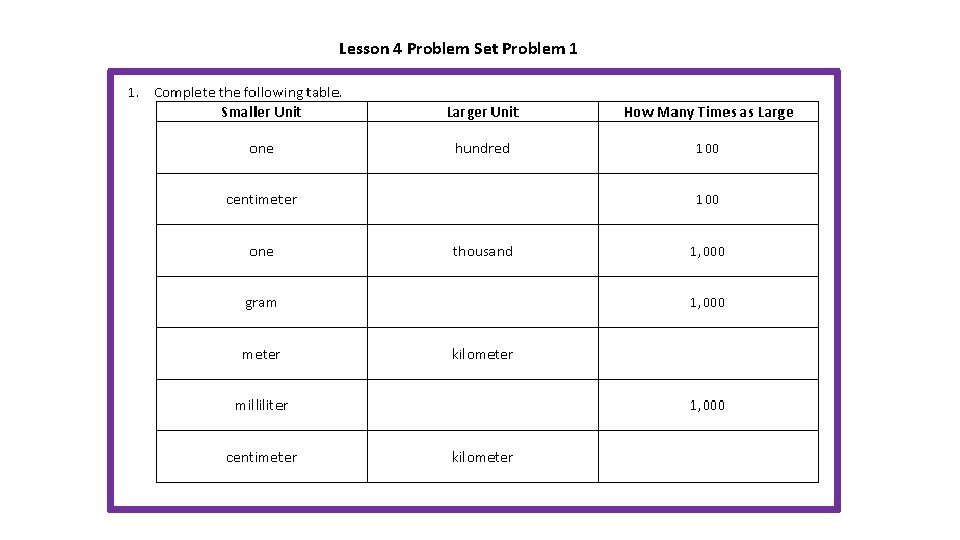
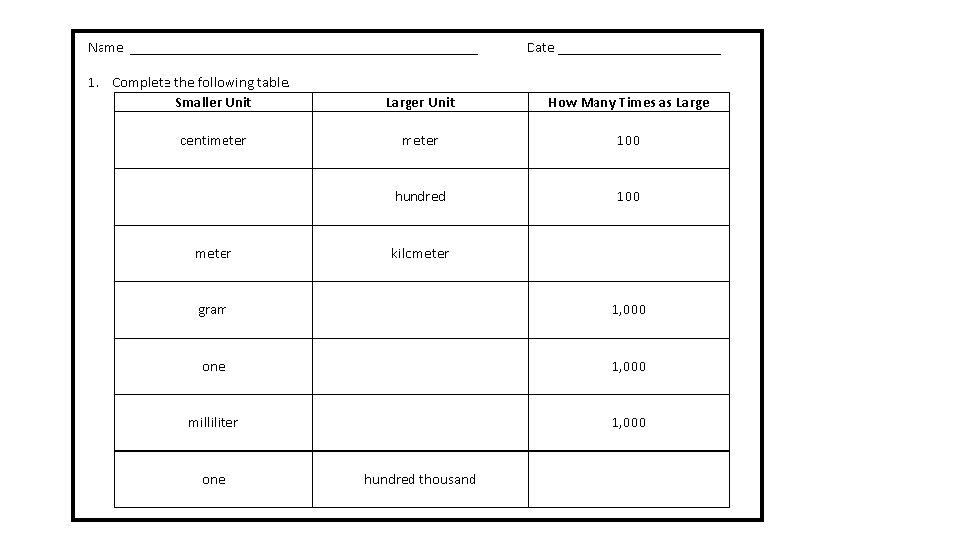
Lesson 4 Problem Set Problem 1

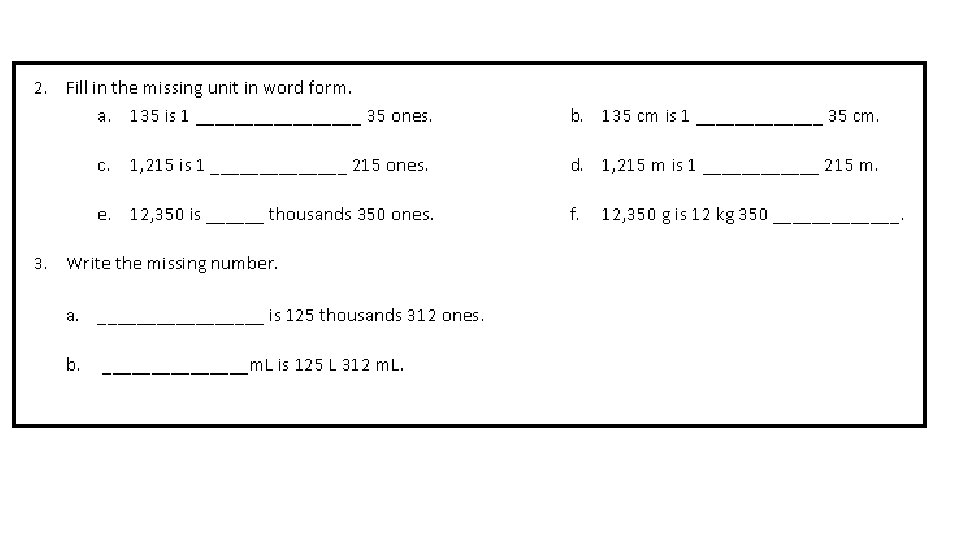
Lesson 4 Problem Set Problems 2 - 4 What patterns did you notice as you solved Problem 2?

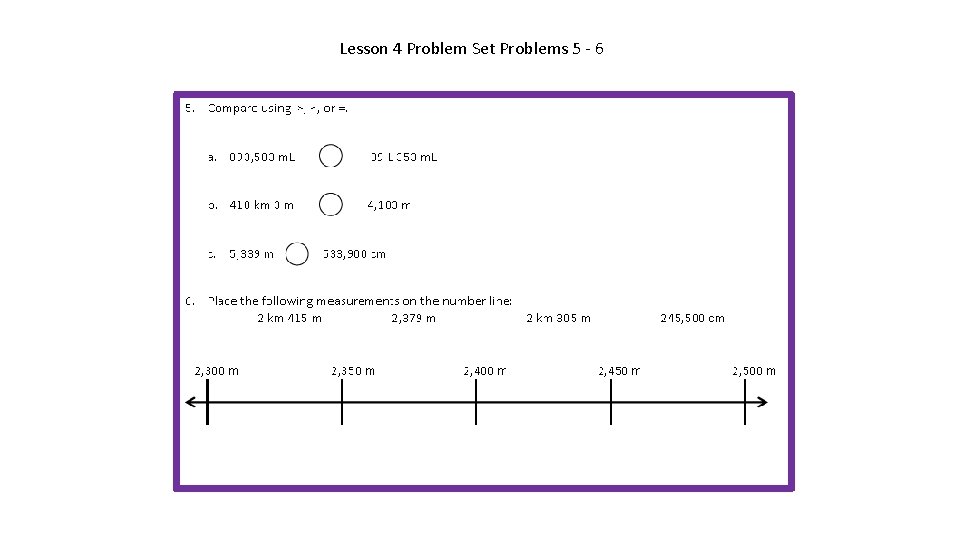
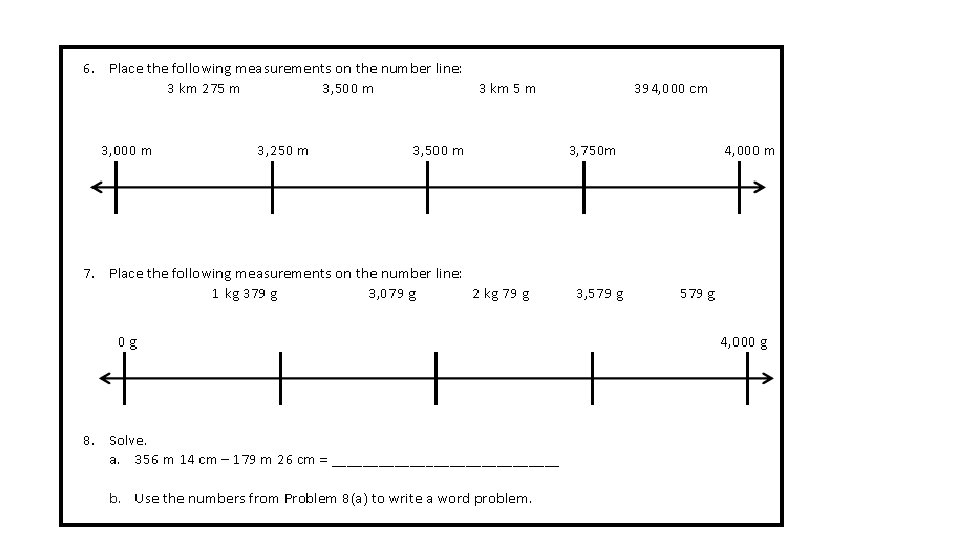
Lesson 4 Problem Set Problems 5 - 6

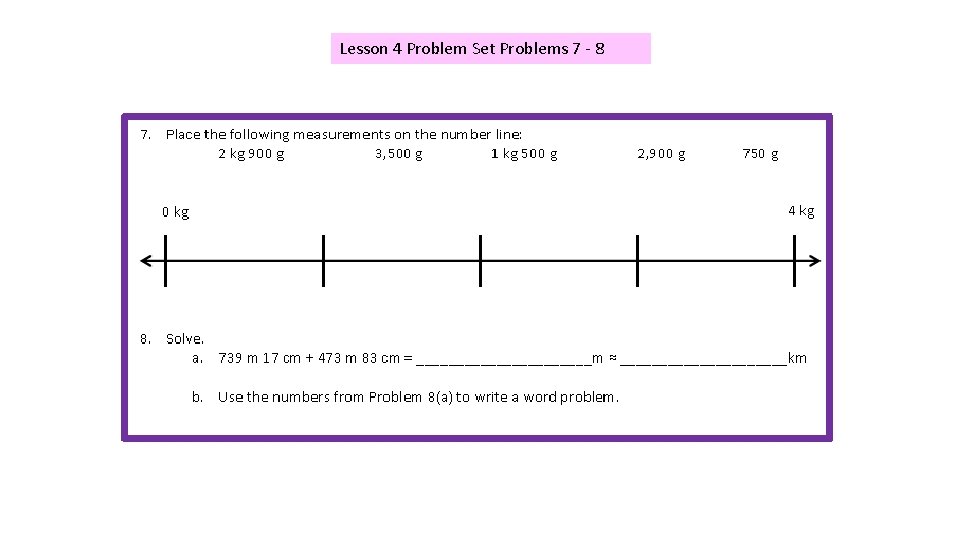
Lesson 4 Problem Set Problems 7 - 8

Debrief Lesson Objective: Know and relate metric units to place value units in order express measurements in different units. Problem Set Debrief Lesson 4 • Explain to your partner how to find the number of centimeters in 1 kilometer. Did you relate each unit to meters? Place value? • Do you find the number line helpful when comparing measures? Why or why not? • How are metric units and place value units similar? Different? Do money units relate to place value units similarly? Time units? • How did finding the amount of water that evaporated from Adam’s beaker (in the Application Problem) connect to place value? • How did the previous lessons on conversions prepare you for today’s lesson?

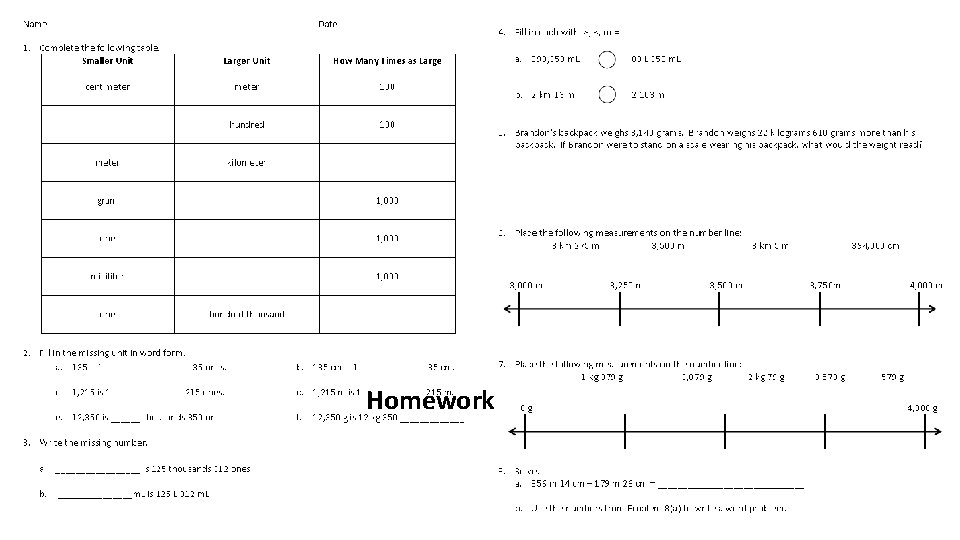
Homework