Module 2 Topic A Lesson 3 Metric Unit

Module 2 Topic A Lesson 3 Metric Unit Conversions 4. MD. 1 and 4. MD. 2

Lesson 3 Objective • Express metric capacity measurements in terms of a smaller unit • Model and solve addition and subtraction word problems involving metric capacity

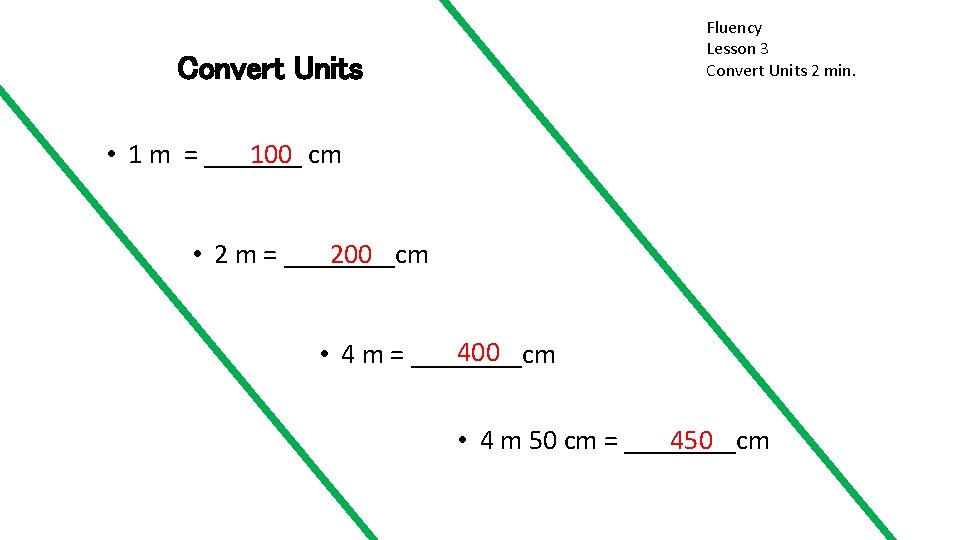
Fluency Lesson 3 Convert Units 2 min. Convert Units 100 cm • 1 m = _______ 200 • 2 m = ____cm 400 • 4 m = ____cm • 4 m 50 cm = ____cm 450

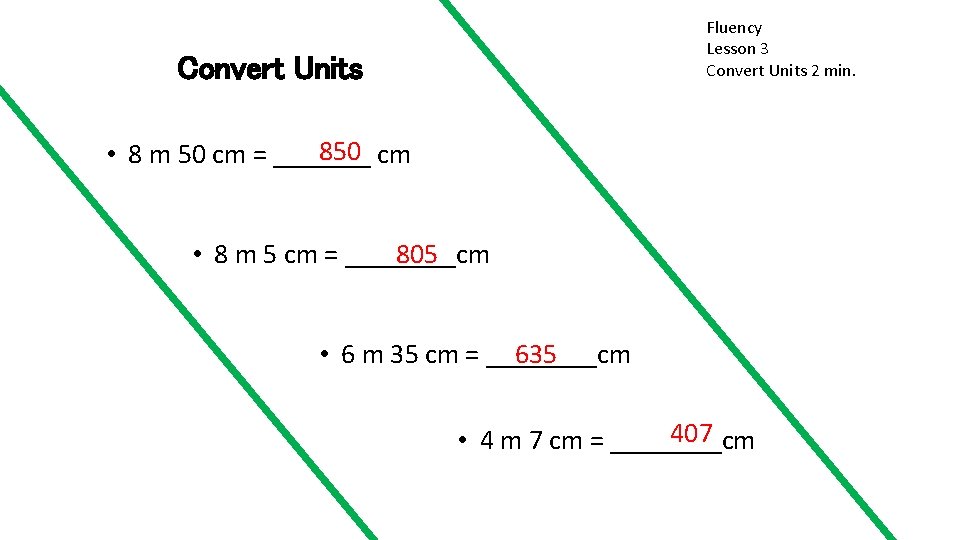
Fluency Lesson 3 Convert Units 2 min. Convert Units 850 cm • 8 m 50 cm = _______ 805 • 8 m 5 cm = ____cm • 6 m 35 cm = ____cm 635 407 • 4 m 7 cm = ____cm

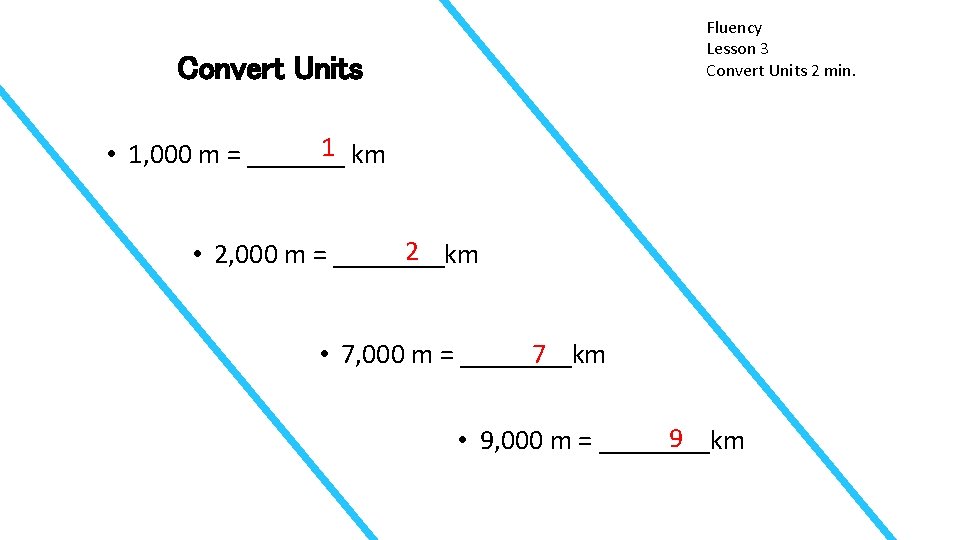
Fluency Lesson 3 Convert Units 2 min. Convert Units 1 km • 1, 000 m = _______ 2 • 2, 000 m = ____km 7 • 7, 000 m = ____km 9 • 9, 000 m = ____km

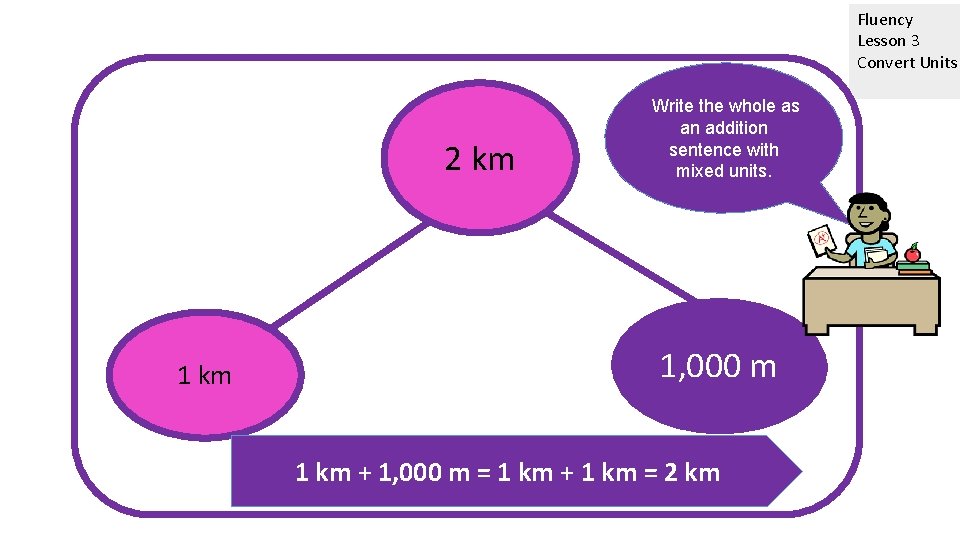
Fluency Lesson 3 Convert Units 2 km 1 km Write the whole as an addition sentence with mixed units. 1, 000 ? m m 1 km + 1, 000 m = 1 km + 1 km = 2 km

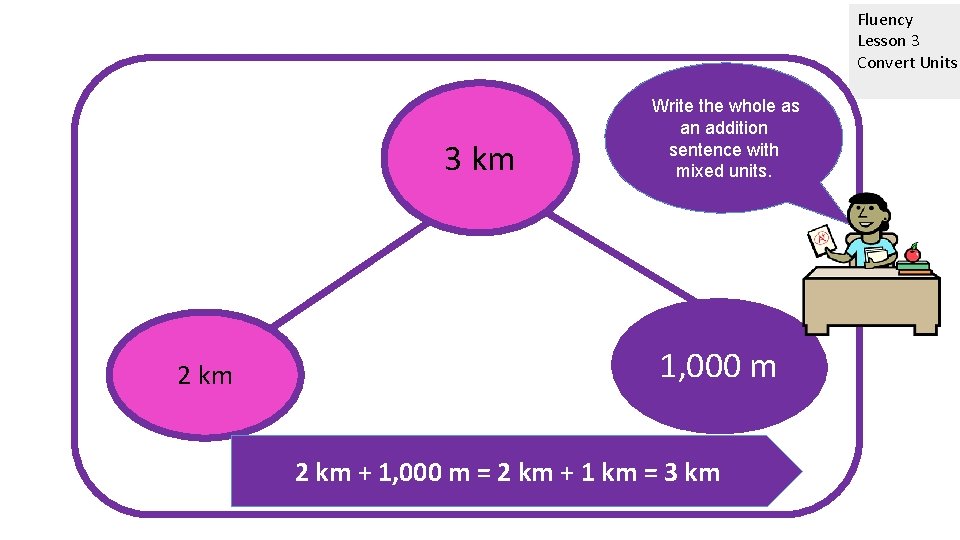
Fluency Lesson 3 Convert Units 3 km 2 km Write the whole as an addition sentence with mixed units. 1, 000 ? m m 2 km + 1, 000 m = 2 km + 1 km = 3 km

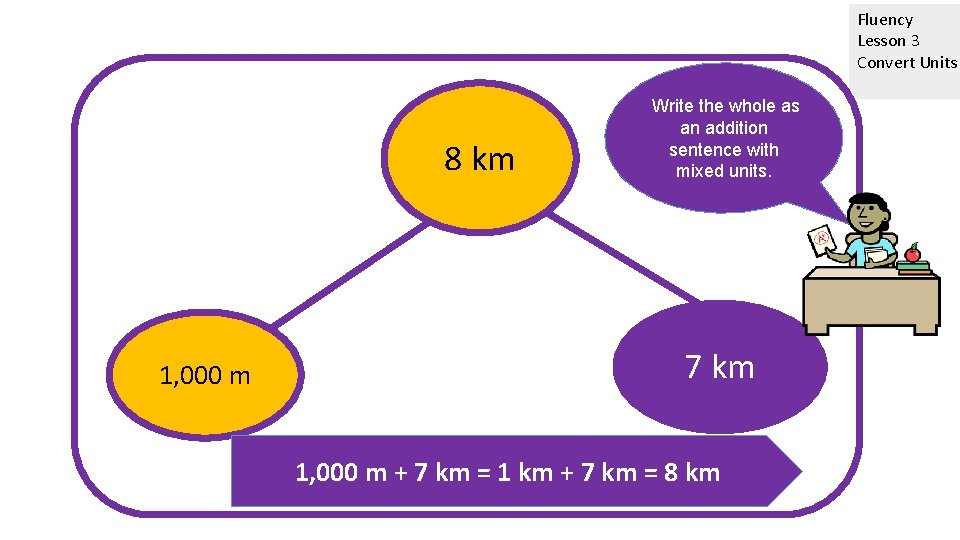
Fluency Lesson 3 Convert Units 8 km 1, 000 m Write the whole as an addition sentence with mixed units. km 7? km 1, 000 m + 7 km = 1 km + 7 km = 8 km

Fluency Lesson 3 Unit counting (4 minutes) • Count by grams in the following sequence and change directions when you see the arrow. • • • 500 g 1, 000 g 1, 500 g 2, 000 g 2, 500 g 3, 000 g • • • 2, 500 g 2, 000 g 1, 500 g 1, 000 g 500 g 0 g You did it!

Fluency Lesson 3 Unit counting (4 minutes) • Count by grams in the following sequence and change directions when you see the arrow. • • • 500 g 1 kg 1, 500 g 2 kg 2, 500 g 3 kg • • • 2, 500 g 2 kg 1, 500 g 1 kg 500 g You did it!

Fluency Lesson 3 Unit counting (4 minutes) • Count by grams in the following sequence and change directions when you see the arrow. • • • 500 g 1 kg 500 g 2 kg 500 g 3 kg • • • 2 kg 500 g 2 kg 1 kg 500 g You did it!

Unit counting (4 minutes) • Count by grams in the following sequence. You will not change directions. • 200 g • 400 g • 600 g • 800 g • 1 kg 200 g You • 1 kg 400 g did it! • 1 kg 600 g • 1 kg 800 g • 2 kg Fluency Lesson 3

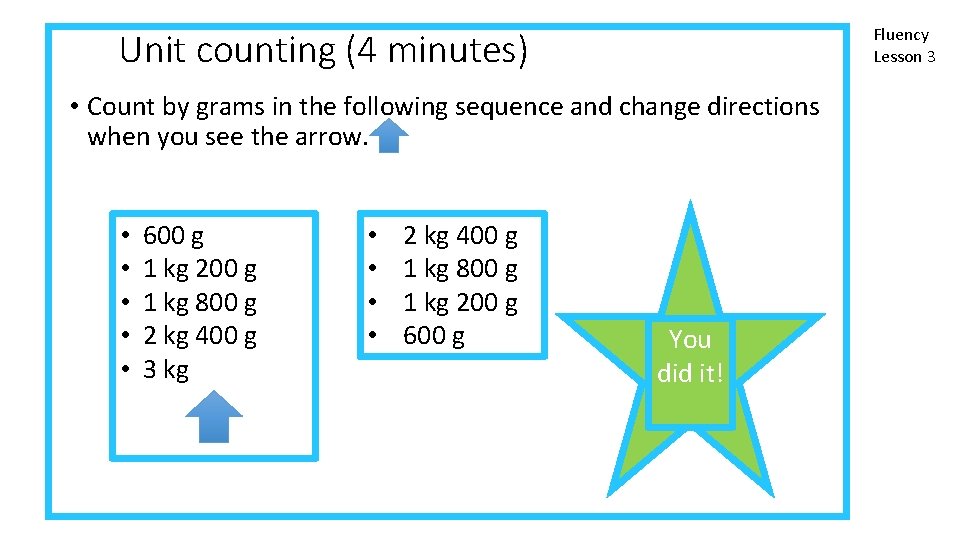
Fluency Lesson 3 Unit counting (4 minutes) • Count by grams in the following sequence and change directions when you see the arrow. • • • 600 g 1, 200 g 1, 800 g 2, 400 g 3 kg • • 2, 400 g 1, 800 g 1, 200 g 600 g You did it!

Fluency Lesson 3 Unit counting (4 minutes) • Count by grams in the following sequence and change directions when you see the arrow. • • • 600 g 1 kg 200 g 1 kg 800 g 2 kg 400 g 3 kg • • 2 kg 400 g 1 kg 800 g 1 kg 200 g 600 g You did it!

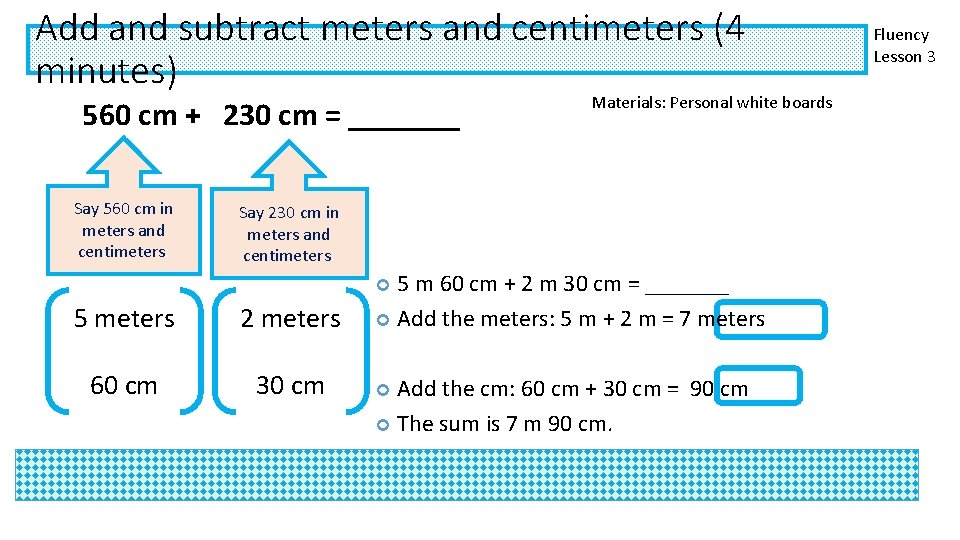
Add and subtract meters and centimeters (4 minutes) 560 cm + 230 cm = _______ Say 560 cm in meters and centimeters. Materials: Personal white boards Say 230 cm in meters and centimeters. 5 m 60 cm + 2 m 30 cm = _______ Add the meters: 5 m + 2 m = 7 meters 5 meters 2 meters 60 cm 30 cm Add the cm: 60 cm + 30 cm = 90 cm The sum is 7 m 90 cm. Fluency Lesson 3

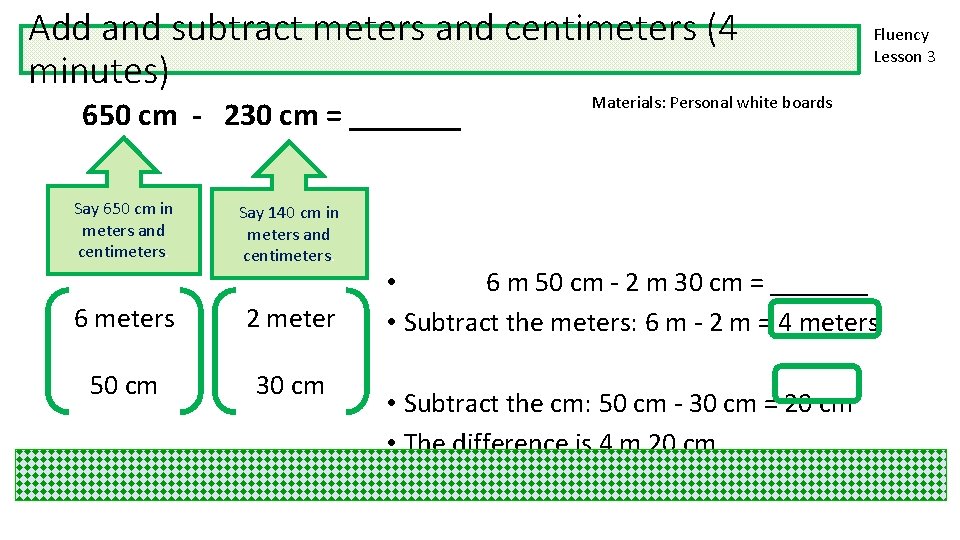
Add and subtract meters and centimeters (4 minutes) 650 cm - 230 cm = _______ Say 650 cm in meters and centimeters. Say 140 cm in meters and centimeters. 6 meters 2 meter 50 cm 30 cm Fluency Lesson 3 Materials: Personal white boards • 6 m 50 cm - 2 m 30 cm = _______ • Subtract the meters: 6 m - 2 m = 4 meters • Subtract the cm: 50 cm - 30 cm = 20 cm • The difference is 4 m 20 cm.

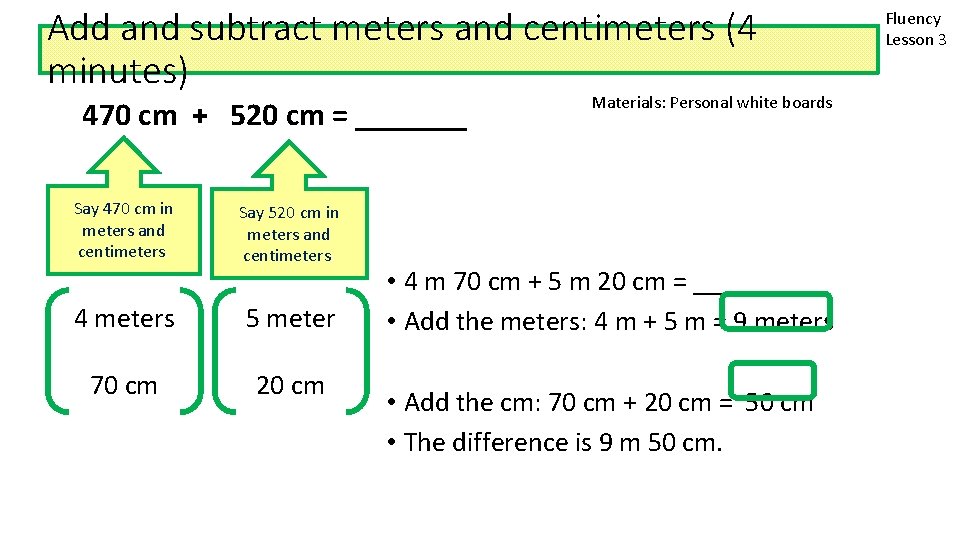
Add and subtract meters and centimeters (4 minutes) 470 cm + 520 cm = _______ Say 470 cm in meters and centimeters. Say 520 cm in meters and centimeters. 4 meters 5 meter 70 cm 20 cm Materials: Personal white boards • 4 m 70 cm + 5 m 20 cm = _______ • Add the meters: 4 m + 5 m = 9 meters • Add the cm: 70 cm + 20 cm = 50 cm • The difference is 9 m 50 cm. Fluency Lesson 3

Application Problem 8 minutes Application Problem Lesson 3 The Lee family had 3 liters of water. Each liter of water weighs 1 kilogram. At the end of the day, they have 290 grams of water left. How much water did they drink? Draw a tape model and solve using mental math or an algorithm.

Concept Development minutes 30 Materials: • Several 3 -liter beakers with measurements of liters and milliliters • Water • Personal white boards

Concept Development Lesson 3 Problem 1 Directions: Compare the sizes and note the relationship between 1 liter and 1 milliliters. • Look at the mark on your beaker that says 1 liter. • Pour water into your beaker until you reach that amount. • How many milliliters are in your beaker? • 1, 000 m. L • How do you know? • 1 liter is the same as 1, 000 milliliters. The beaker shows that the measurements are the same.

1 L = 1, 000 ml Concept Development Lesson 3 Problem 1 • With your partner, locate 1, 500 milliliters and pour in more water to measure 1, 500 m. L. • How many liters do you have? • Less than 2 L but more than 1 L. 1 liter 500 milliliters. • Yes, we just named mixed unit of grams and kilograms in our previous lesson. Now we will can use mixed units of liters and milliliters by using both sides of the scale of the beaker.

Concept Development Lesson 3 Problem 1 • Pour water to measure liters. How many milliliters equals 2 liters? 1 L 500 m. L = 1, 500 m. L • 2, 000 m. L • Pour more water to measure 2, 200 m. L of water. How many liters equals 2, 200 m. L? • 2 L 200 m. L

• I have several beakers of different amounts of water prepared. You will circulate to each beaker, recording the amount of water as mixed units of liters and milliliters. Lesson 3 Problem 1 • We will now compare answers as a class and record finding on the board to show equivalency between Activity units of liters and milliliters.

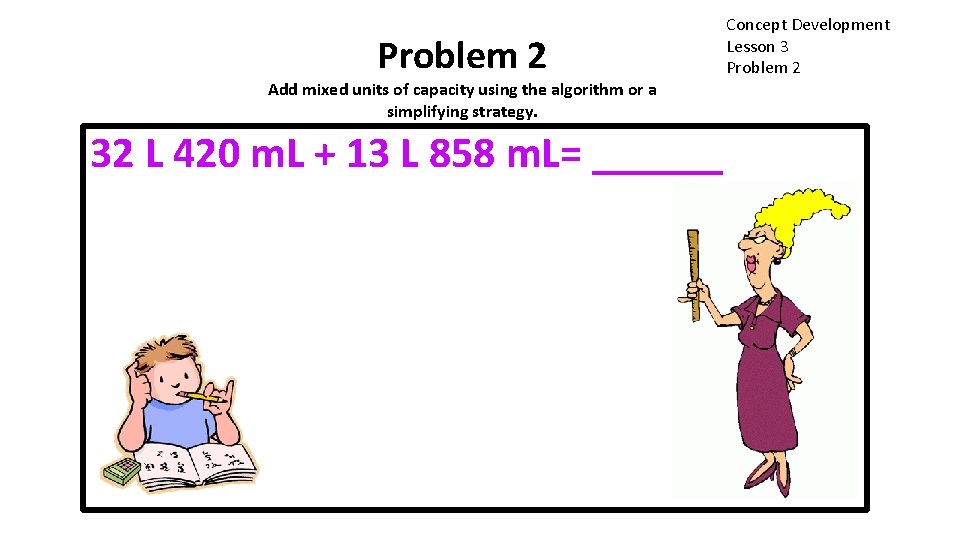
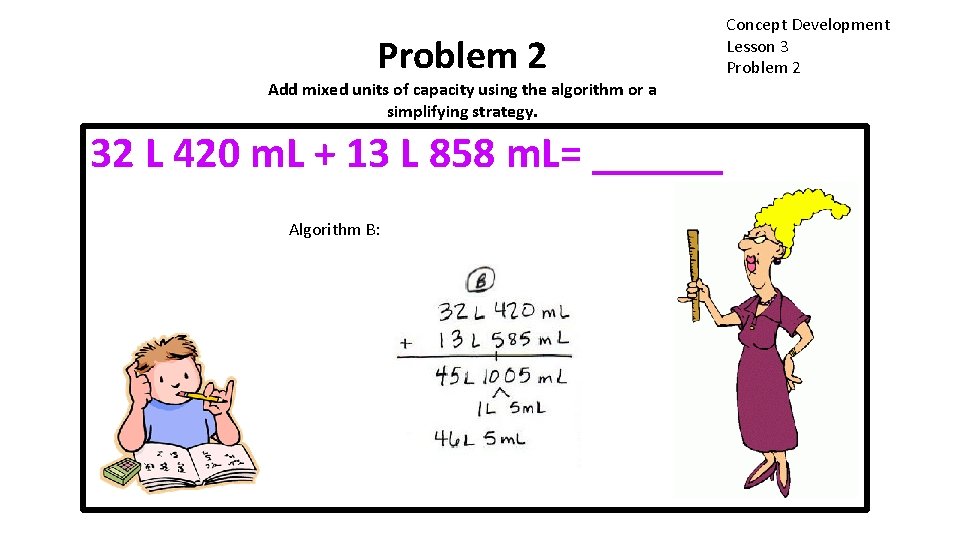
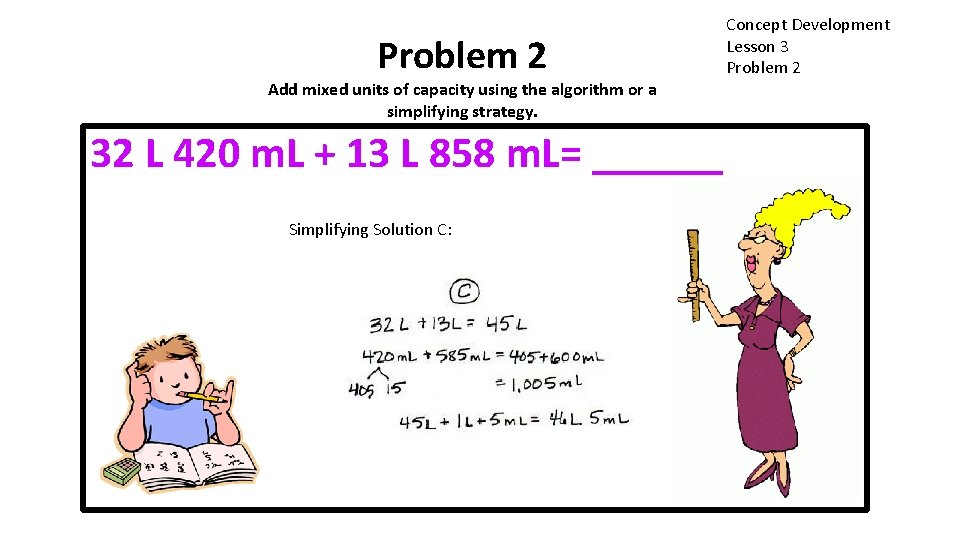
Problem 2 Add mixed units of capacity using the algorithm or a simplifying strategy. 32 L 420 m. L + 13 L 858 m. L= ______ A simplifying strategy because 420 m. L Choose the way you want to do it. Ifand decomposed to 15 ml and 5 m. L There are someis up, try you 400 finish before two minutes I can solve it. Let’s mentally m. L plus 585 makes 600 m. L. 600 solving a different way. have so 5 an m. Lrenamings + 400 m. L is 1 L with m. L lefttwo over. and then check my pairs of students work at the board, 46 liters 5 milliliters. algorithm work one pair using thecould algorithm, one pair work with an algorithm. recording a simplifying too. strategy. What strategy would you use? Concept Development Lesson 3 Problem 2

Problem 2 Add mixed units of capacity using the algorithm or a simplifying strategy. 32 L 420 m. L + 13 L 858 m. L= ______ Concept Development Lesson 3 Problem 2

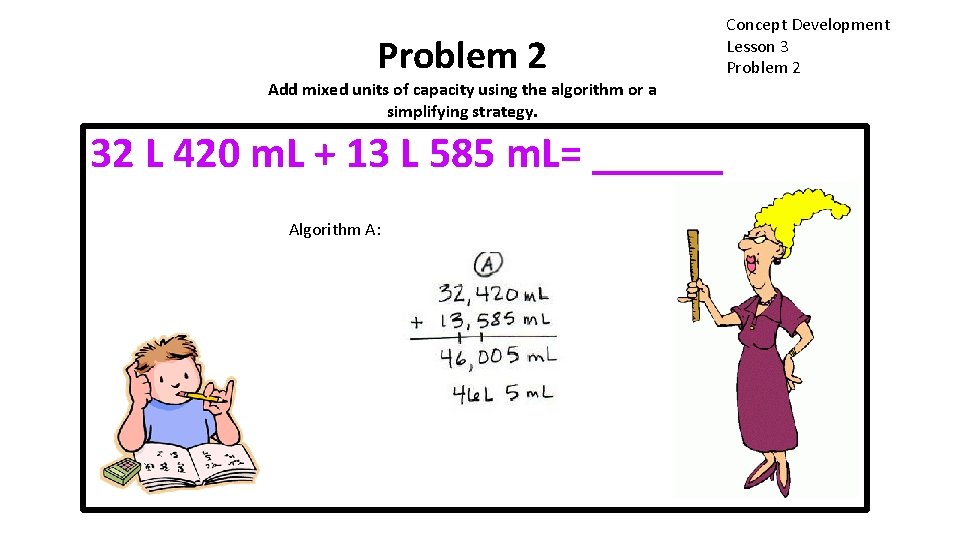
Problem 2 Add mixed units of capacity using the algorithm or a simplifying strategy. 32 L 420 m. L + 13 L 585 m. L= ______ Algorithm A: Concept Development Lesson 3 Problem 2

Problem 2 Add mixed units of capacity using the algorithm or a simplifying strategy. 32 L 420 m. L + 13 L 858 m. L= ______ Algorithm B: Concept Development Lesson 3 Problem 2

Problem 2 Add mixed units of capacity using the algorithm or a simplifying strategy. 32 L 420 m. L + 13 L 858 m. L= ______ Simplifying Solution C: Concept Development Lesson 3 Problem 2

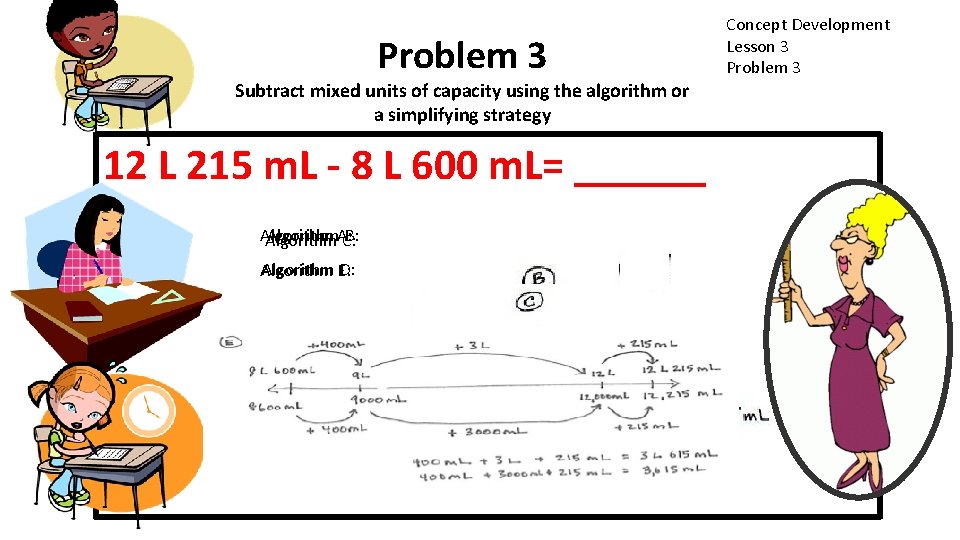
Problem 3 Subtract mixed units of capacity using the algorithm or a simplifying strategy 12 L 215 m. L - 8 L 600 m. L= ______ Oh for sure I’m A simplifying strategy. using the algorithm. strategy or. If 8 you thefinish before We have to rename Choose the way you wanton to do it. I can count from two minutes is up, tryalgorithm? a different way. Let’s a liters 600 solving milliliters. I can do mental math. I’llwork show have two pairs of students at the board, one pair using the algorithm, one pair recording a you when we simplifying strategy. solve. Concept Development Lesson 3 Problem 3

Problem 3 Subtract mixed units of capacity using the algorithm or a simplifying strategy 12 L 215 m. L - 8 L 600 m. L= ______ Algorithm. A: B: Algorithm C: Algorithm E: D: Concept Development Lesson 3 Problem 3

Problem 4 Solve a word problem involving mixed units of capacity. Concept Development Lesson 3 Problem 4 Jennifer was making 2, 170 milliliters of her favorite drink that combines iced tea and lemonade. If she put in 1 liter 300 milliliters of iced tea, how much lemonade does she need?

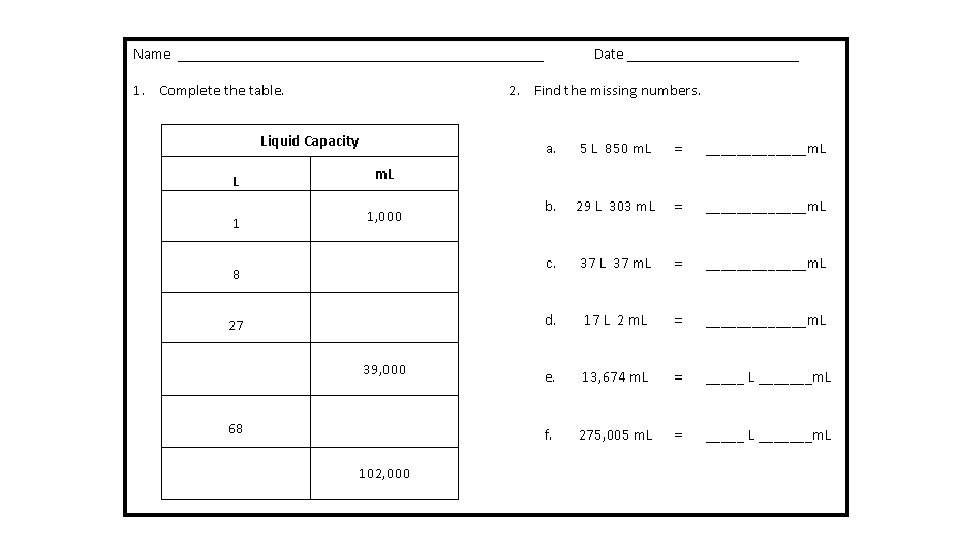
Problem Set (10 Minutes)

Problem Set Lesson 3 Problems 1 and 2

Concept Development Lesson 3 Problem Set Problem 3

Lesson 3 Problem Set Problems 4 and 5 • In Problem 4(a), what was your strategy for ordering the drinks? • Discuss why you chose to solve Problem 5 using mixed units or converting all units to milliliters.

Lesson 3 Problem Set Problem 6

Debrief Lesson Objective: Express metric capacity measurements in terms of a smaller unit; Model and solve addition and subtraction word problems involving metric capacity • Which strategy do you prefer for adding and subtracting mixed units? • Why is one way preferable to the other for you? • What new terms to describe capacity did you learn today? • What patterns have you noticed about the vocabulary used to measure distance, mass, and capacity? • How did the Application Problem connect to today’s lesson? • Describe the relationship between liters and milliliters. • How did today’s lesson relate to the lessons on weight and length? Problem Set Debrief Lesson 3

Homework