Module 2 Topic 2 Solving Linear Equations and

Module 2, Topic 2: Solving Linear Equations and

Properties of Equality

Basic Number Properties

Solve the equation and check your solution. Write the property that justifies each step of your solving strategy. 3(2 x + 1) = 4 x + 6 6 x + 3 = 4 x + 6 2 x + 3 = 2 x = 3 6 Property Distributive Property Subtraction Property of Equality Division Property of Equality ?

• What is a solution When an equation contains a anyway? ? variable, we can solve the equation. • A solution to an equation is a value for the variable that makes the equation a true statement.

Linear Equations can have: • One solution • No solutions • Infinite solutions

One solution: There is one number that, when substituted for the variable, makes the equation true. When you solve for the variable, you will get one real number. 4 x – 6 = 14 4 x = 20 x=5

No solution: There are no numbers that would make the equation true. When you try to solve the equation, you will get a FALSE statement 3 x + 7 = 3 x + 4 -3 x 7≠ 4

Infinite solutions: Using any real number in place of the variable would make the equation true. When you solve the equation, you will get the exact 12 xsame + 4 = thing 4(3 x +on 1) both sides of the 12 x + 4 equation. = 12 x + 4 -12 x 4=4

Determine if the equation has one solution, no solutions, or infinite solutions. Show your work. o 2 t y b term s!) h c a iply e e fraction t l u (M th f o d i get r 3 x + 12 = 3 x – 4 + 17 3 x + 13 = 3 x + 13 ! s n o i t u l o s -3 x e t i n i f n I 13 = 13

Lesson 2: Literal Equations

Forms of Linear General Form Factored Form Standard Form* Equations y = ax + b Example: y = 3 x + 9 y = a(x – c) Example: y = 3(x + 3) *A must be a positive integer Ax + By = C Example: 3 x – y = -9

Changing between forms of linear equations: (Goal: Ax + By = C) y = ¾ x 7 Write the equation y = ¾ x - 7 in property 4 y = 4(¾ x –standard 7) multiplicationform distributive property 4 y = 3 x – 28 addition property 28 + 4 y = 3 x subtraction property 28 = 3 x – 4 y Standard Form 3 x – 4 y = 28

Changing between forms of linear equations: (Goal: y = ax + b) 4 x + 2 y = 24 Write the equation 4 x + 2 y = 24 in subtraction property 2 y = -4 x + 24 general form division property - General form y = -2 x + 12 y = a(x - c) Now, change (Goal: that to factored Factored form y = -2(x – 6) distributive propertyform

Literal Equations: • variables represent specific measures • Seen most often when you study • d = rt formulas • A = ½ bh • Examples: • C = 2πr

Solving Literal Equations

Solving Literal Equations: Example (Goal: isolate “t”) Given the equation d = rt, solve for t d = rt Division property of equality

Solving Literal Equations: Another Example Solve for W: A = 2(L + W) Division property of equality Subtraction property of equality

Lesson 3: Solving Inequalities

Alan’s camping troop is selling popcorn to earn money for an upcoming camping trip. Each camper starts with a credit of $25 toward his sales, and each box of popcorn sells for $3. 75. 1. Write a function, f(b), to show Alan’s total sales as a function of the number of boxes (b) of popcorn he sells. 2. Determine the slope and the y-intercept and explain what they mean in terms of the situation.

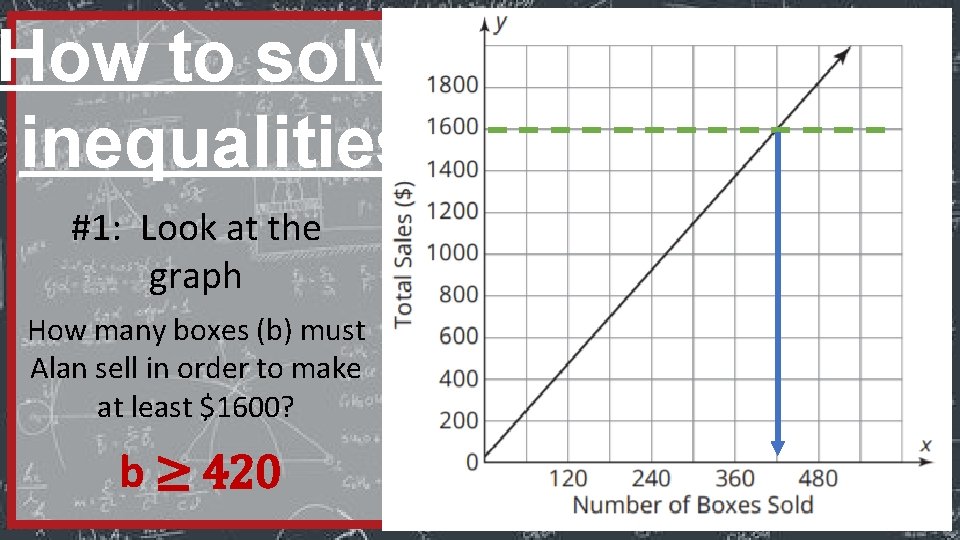
How to solve inequalities #1: Look at the graph How many boxes (b) must Alan sell in order to make at least $1600? b ≥ 420

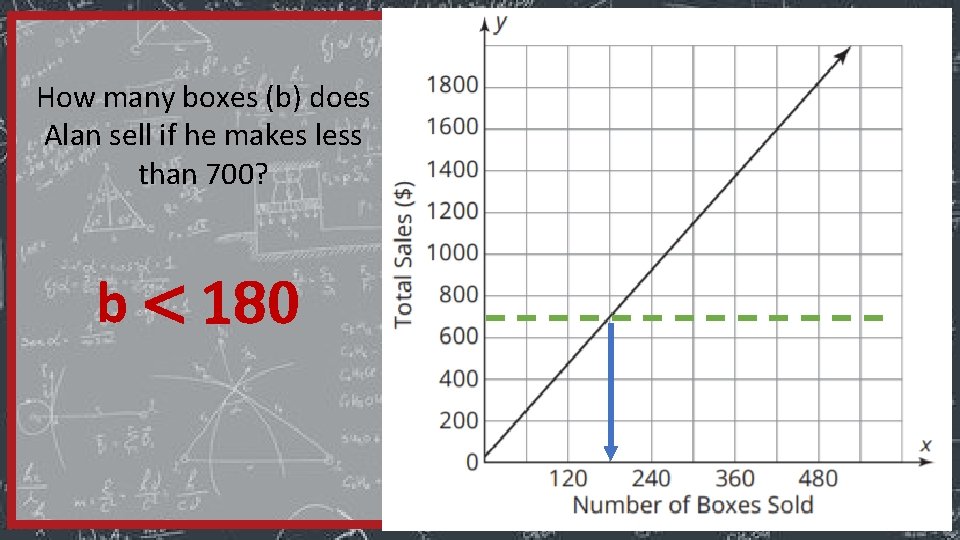
How many boxes (b) does Alan sell if he makes less than 700? b < 180

How to solve inequalities #2: Solve it algebraically It’s almost exactly like solving an equation! One important rule: If you multiply by a negative number, reverse the sign

#2: Solve it algebraically How many boxes (b) must Alan sell in order to make at least $1600? f(b) = 3. 75 b + 25 ≥ 1600 3. 75 b ≥ 1575 3. 75 b ≥ 420 Subtraction Property of Equality Division Property of Equality

#2: Solve it algebraically How many boxes (b) does Alan sell if he makes less than 700? f(b) = 3. 75 b + 25 < 700 3. 75 b < 675 3. 75 b < 180 Subtraction Property of Equality Division Property of Equality

#2: Solve it algebraically Try solving this one: -3 x + 35 > 47 -3 x > 12 -3 Subtraction Property of Equality -3 x < -4 Division Property of Equality One important rule: If you multiply by a negative number, reverse the sign

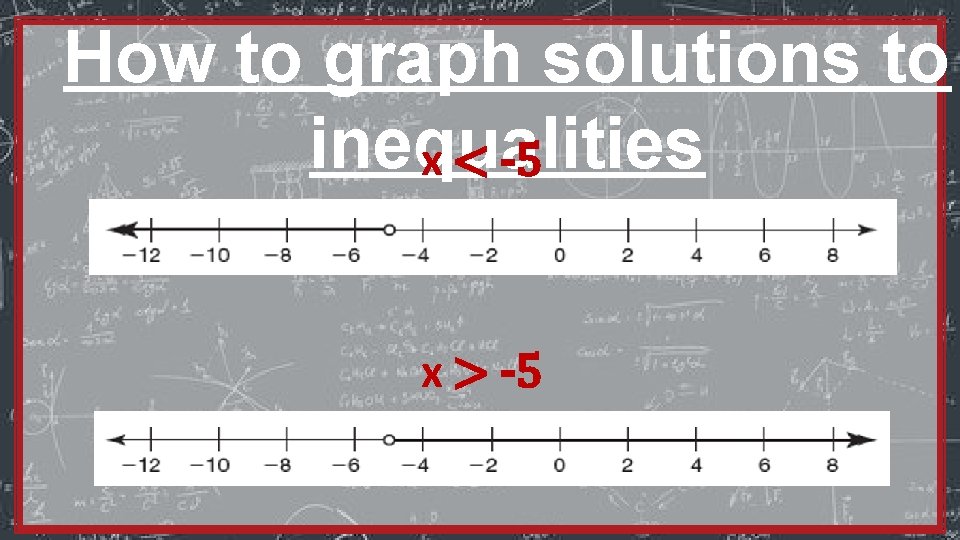
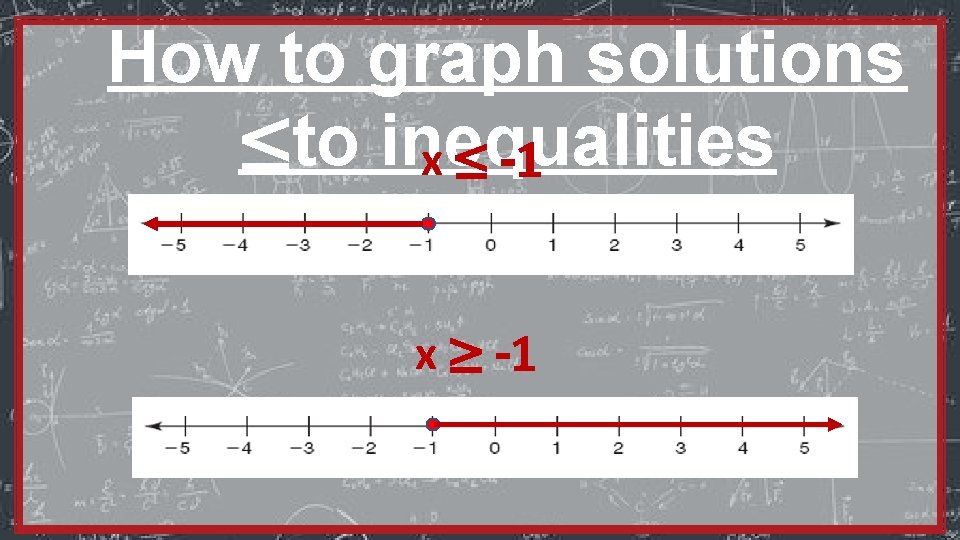
How to graph solutions to inequalities Ø Put a dot and a line on the number line. o Open circle does not include the number (< or >) • Closed circle includes the number (≤ or ≥)

How to graph solutions to inequalities x < -5 x > -5

How to graph solutions ≤to inequalities x ≤ -1 x ≥ -1

One important rule: If you multiply by a negative number, reverse the sign

Lesson 4: Compound Inequalities

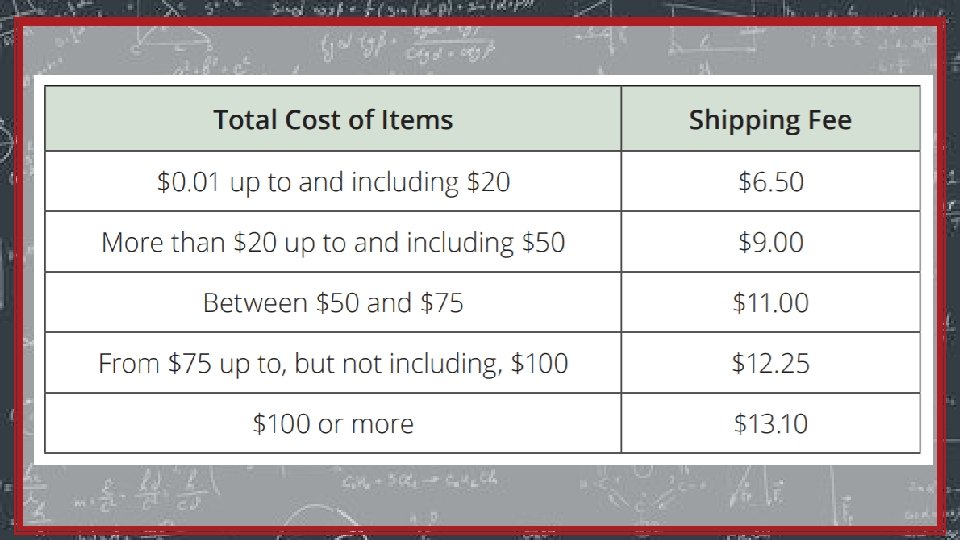
(x) 0. 01 ≤ x ≤ 20 20 < x ≤ 50 50 < x < 75 75 ≤ x < 100 ≤ x

Compound Two simple inequalities are combined. Inequalities 1. Disjunction: • The union of two simple inequalities • Key word: “OR” • ONE condition has to be satisfied

Example: To get the discount movie ticket price, you must be under 12 years old or 65 and up. Disjunction/Union 65 ≤ x x < 12 1 5 10 15 55 20 60 65 70 75 x < 12 or 65 ≤ x 10 20 30 40 50 60 70 80 90

How to solve Unions: Solve each side and keep the “or” in between them x + 5 > 14 -5 -5 OR x>9 0 1 2 3 x < 9 3 3 x<3 3 4 5 6 7 8 9 10 11 12

Compound Two simple inequalities are combined. Inequalities 2. Conjunction: • The intersection of two simple inequalities. • Key word: “AND” • BOTH condition must be satisfied

Example: To enlist in the United States army, you must be at least. Intersection 17 years old and younger than 35. 17 ≤ x x < 35 17 ≤ x and x < 35

Conjunctions Compact form: (“AND”) 17 ≤ x and x < 35 Can be written as: 17 ≤ x < 35

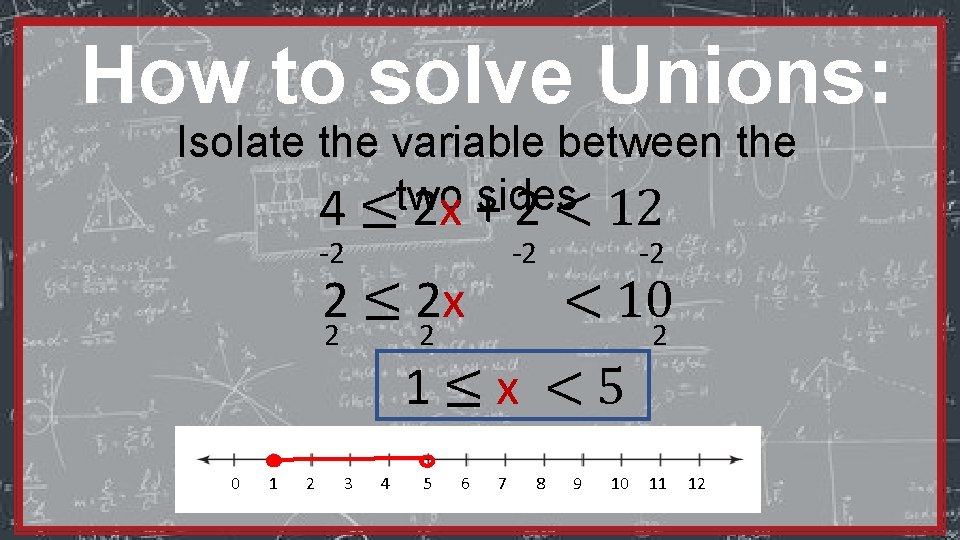
How to solve Unions: Isolate the variable between the two sides 4 ≤ 2 x + 2 < 12 -2 -2 2 ≤ 2 x 2 0 1 2 -2 < 10 2 1≤x <5 3 4 5 6 7 8 9 10 2 11 12