Module 2 Bayesian Hierarchical Models Francesca Dominici Michael

Module 2: Bayesian Hierarchical Models Francesca Dominici Michael Griswold The Johns Hopkins University Bloomberg School of Public Health 2005 Hopkins Epi-Biostat Summer Institute 1

Key Points from yesterday n “Multi-level” Models: ¨ Have covariates from many levels and their interactions ¨ Acknowledge correlation among observations from within a level (cluster) n Random effect MLMs condition on unobserved “latent variables” to describe correlations n Random Effects models fit naturally into a Bayesian paradigm n Bayesian methods combine prior beliefs with the likelihood of the observed data to obtain posterior inferences 2005 Hopkins Epi-Biostat Summer Institute 2

Bayesian Hierarchical Models n Module 2: ¨ Example 1: School Test Scores n The simplest two-stage model n Win. BUGS ¨ Example 2: Aww Rats n A normal hierarchical model for repeated measures n Win. BUGS 2005 Hopkins Epi-Biostat Summer Institute 3

Example 1: School Test Scores 2005 Hopkins Epi-Biostat Summer Institute 4

Testing in Schools n Goldstein et al. (1993) n Goal: differentiate between `good' and `bad‘ schools n Outcome: Standardized Test Scores n Sample: 1978 students from 38 schools ¨ n MLM: students (obs) within schools (cluster) Possible Analyses: 1. Calculate each school’s observed average score 2. Calculate an overall average for all schools 3. Borrow strength across schools to improve individual school estimates 2005 Hopkins Epi-Biostat Summer Institute 5

Testing in Schools n Why borrow information across schools? ¨ Median # of students per school: 48, Range: 1 -198 ¨ Suppose small school (N=3) has: 90, 10 (avg=63) ¨ Suppose large school (N=100) has avg=65 ¨ Suppose school with N=1 has: 69 (avg=69) ¨ Which school is ‘better’? ¨ Difficult to say, small N highly variable estimates ¨ For larger schools we have good estimates, for smaller schools we may be able to borrow information from other schools to obtain more accurate estimates ¨ How? Bayes 2005 Hopkins Epi-Biostat Summer Institute 6

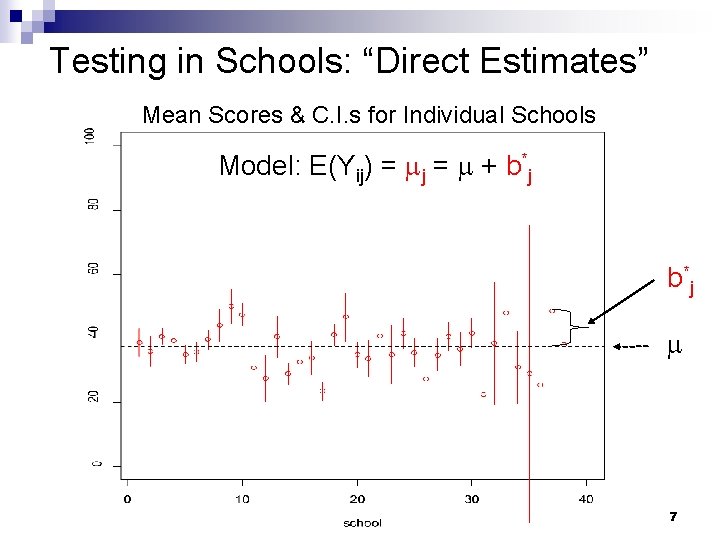
Testing in Schools: “Direct Estimates” Mean Scores & C. I. s for Individual Schools Model: E(Yij) = j = + b*j b *j 2005 Hopkins Epi-Biostat Summer Institute 7

Fixed and Random Effects n Standard Normal regression models: ij ~ N(0, 2) 1. Yij = + ij j = X (overall avg) 2. Yij = j + ij j = Xj (shool avg) = + b*j + ij = X + b*j = X + (Xj – X) 2005 Hopkins Epi-Biostat Summer Institute Fixed Effects 8

Fixed and Random Effects n Standard Normal regression models: ij ~ N(0, 2) 1. Yij = + ij j = X (overall avg) 2. Yij = j + ij j = Xj (shool avg) = + b*j + ij n = X + b*j = X + (Xj – X) Fixed Effects A random effects model: 3. Yij | bj = + bj + ij, with: bj ~ N(0, 2) Random Effects Represents Prior beliefs about similarities between schools! 2005 Hopkins Epi-Biostat Summer Institute 9

Fixed and Random Effects n Standard Normal regression models: ij ~ N(0, 2) 1. Yij = + ij j = X (overall avg) 2. Yij = j + ij j = Xj (shool avg) = + b*j + ij n = X + b*j = X + (Xj – X) Fixed Effects A random effects model: 3. Yij | bj = + bj + ij, with: bj ~ N(0, 2) Random Effects j = X + bjblup = X + ¨ ¨ b*j = X + (Xj – X) Estimate is part-way between the model and the data Amount depends on variability ( ) and underlying truth ( ) 10 2005 Hopkins Epi-Biostat Summer Institute

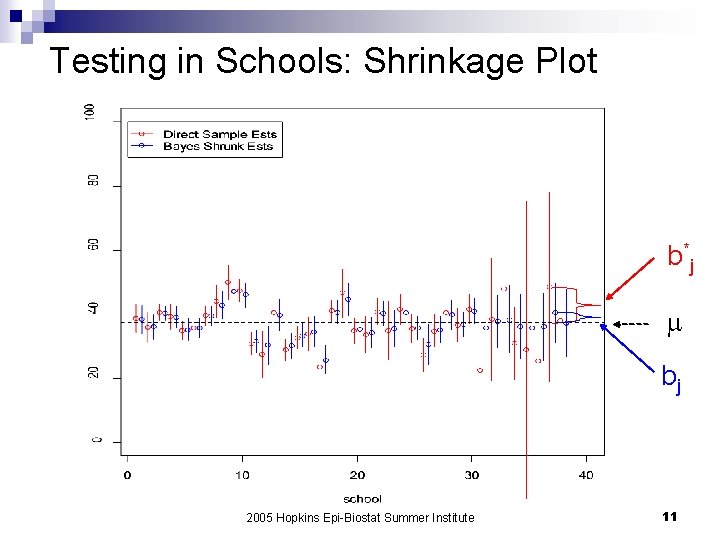
Testing in Schools: Shrinkage Plot b *j bj 2005 Hopkins Epi-Biostat Summer Institute 11

Testing in Schools: Winbugs Data: i=1. . 1978 (students), s=1… 38 (schools) n Model: ¨ Yis ~ Normal( s , 2 y) ¨ s ~ Normal( , 2 ) (priors on school avgs) n Note: Win. BUGS uses precision instead of variance to specify a normal distribution! n Win. BUGS: ¨ Yis ~ Normal( s , y) with: 2 y = 1 / y ¨ s ~ Normal( , ) with: 2 = 1 / 2005 Hopkins Epi-Biostat Summer Institute 12

Testing in Schools: Winbugs Win. BUGS Model: ¨ Yis ~ Normal( s , y) with: 2 y = 1 / y ¨ s ~ Normal( , ) with: 2 = 1 / ¨ y ~ (0. 001, 0. 001) (prior on precision) n Hyperpriors n ¨ Prior on mean of school means n ~ Normal(0 , 1/1000000) ¨ Prior on precision (inv. variance) of school means n ~ (0. 001, 0. 001) n Using “Vague” / “Noninformative” Priors 2005 Hopkins Epi-Biostat Summer Institute 13

Testing in Schools: Winbugs n Full Win. BUGS Model: ¨ Yis ~ Normal( s , y) with: 2 y = 1 / y ¨ s ~ Normal( , ) with: 2 = 1 / ¨ y ~ (0. 001, 0. 001) ¨ ~ Normal(0 , 1/1000000) ¨ ~ (0. 001, 0. 001) 2005 Hopkins Epi-Biostat Summer Institute 14

Testing in Schools: Winbugs Win. BUGS Code: model { for( i in 1 : N ) { Y[i] ~ dnorm(mu[i], y. tau) mu[i] <- alpha[school[i]] } for( s in 1 : M ) { alpha[s] ~ dnorm(alpha. c, alpha. tau) } y. tau ~ dgamma(0. 001, 0. 001) sigma <- 1 / sqrt(y. tau) alpha. c ~ dnorm(0. 0, 1. 0 E-6) alpha. tau ~ dgamma(0. 001, 0. 001) } n 2005 Hopkins Epi-Biostat Summer Institute 15

Example 2: Aww, Rats… A normal hierarchical model for repeated measures 2005 Hopkins Epi-Biostat Summer Institute 16

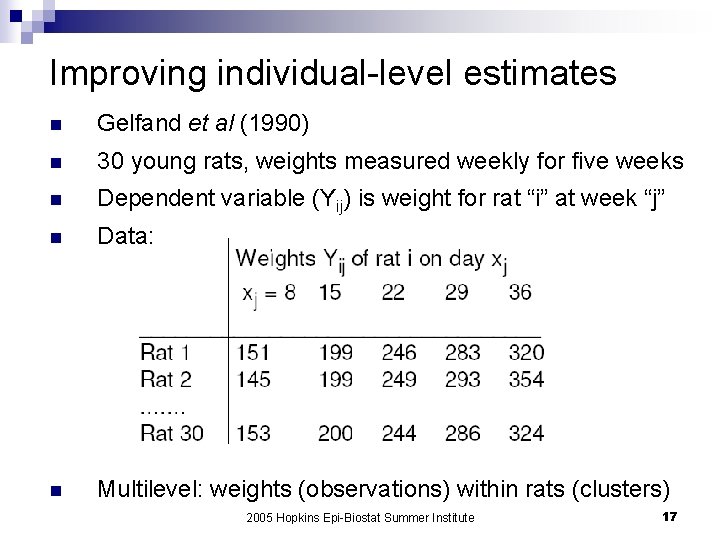
Improving individual-level estimates n Gelfand et al (1990) n 30 young rats, weights measured weekly for five weeks n Dependent variable (Yij) is weight for rat “i” at week “j” n Data: n Multilevel: weights (observations) within rats (clusters) 2005 Hopkins Epi-Biostat Summer Institute 17

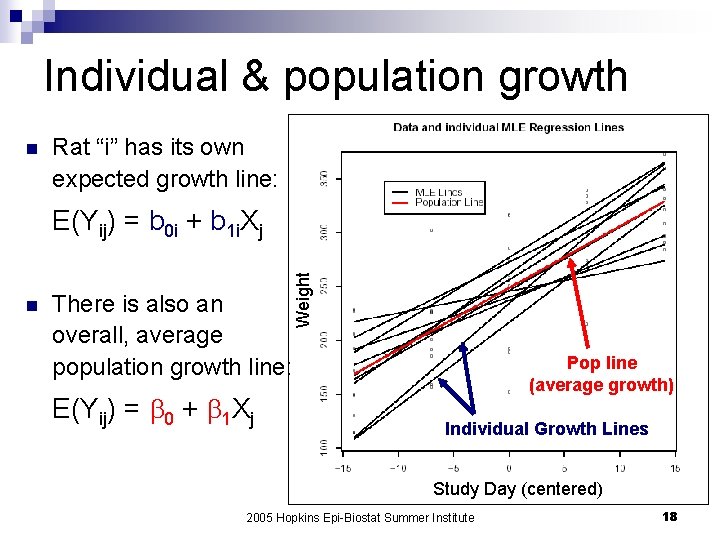
Individual & population growth n Rat “i” has its own expected growth line: n There is also an overall, average population growth line: E(Yij) = 0 + 1 Xj Weight E(Yij) = b 0 i + b 1 i. Xj Pop line (average growth) Individual Growth Lines Study Day (centered) 2005 Hopkins Epi-Biostat Summer Institute 18

Improving individual-level estimates n Possible Analyses 1. Each rat (cluster) has its own line: intercept= bi 0, slope= bi 1 2. All rats follow the same line: bi 0 = 0 , bi 1 = 1 3. A compromise between these two: Each rat has its own line, BUT… the lines come from an assumed distribution E(Yij | bi 0, bi 1) = bi 0 + bi 1 Xj “Random Effects” bi 0 ~ N( 0 , 02) bi 1 ~ N( 1 , 12) 2005 Hopkins Epi-Biostat Summer Institute 19

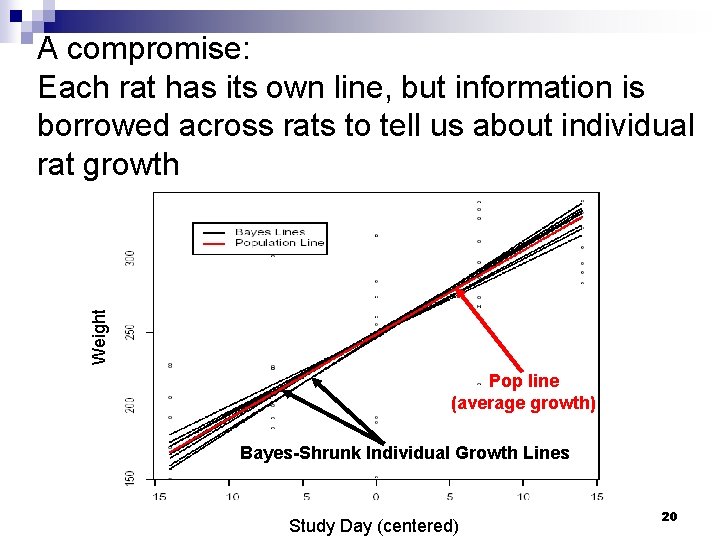
Weight A compromise: Each rat has its own line, but information is borrowed across rats to tell us about individual rat growth Pop line (average growth) Bayes-Shrunk Individual Growth Lines 2005 Hopkins Epi-Biostat Summer Institute Study Day (centered) 20

Rats: Winbugs (see help: Examples Vol I) n Win. BUGS Model: 2005 Hopkins Epi-Biostat Summer Institute 21

Rats: Winbugs (see help: Examples Vol I) n Win. BUGS Code: 2005 Hopkins Epi-Biostat Summer Institute 22

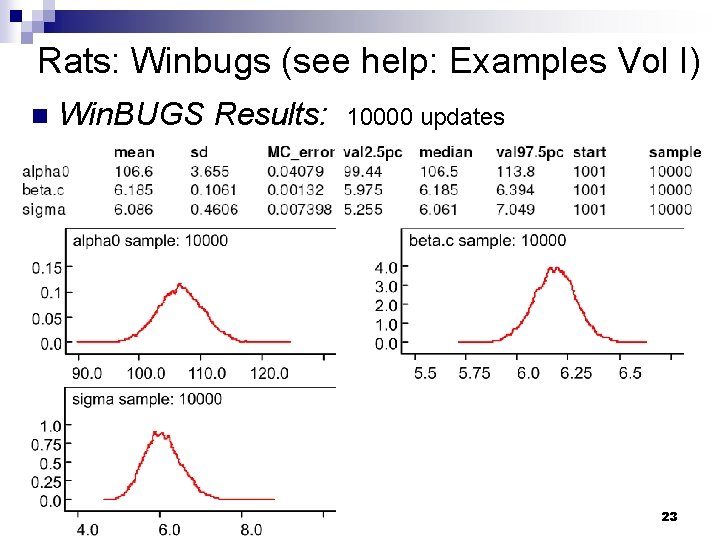
Rats: Winbugs (see help: Examples Vol I) n Win. BUGS Results: 10000 updates 2005 Hopkins Epi-Biostat Summer Institute 23

Win. BUGS Diagnostics: n n n MC error tells you to what extent simulation error contributes to the uncertainty in the estimation of the mean. This can be reduced by generating additional samples. Always examine the trace of the samples. To do this select the history button on the Sample Monitor Tool. Look for: ¨ Trends ¨ Correlations 2005 Hopkins Epi-Biostat Summer Institute 24

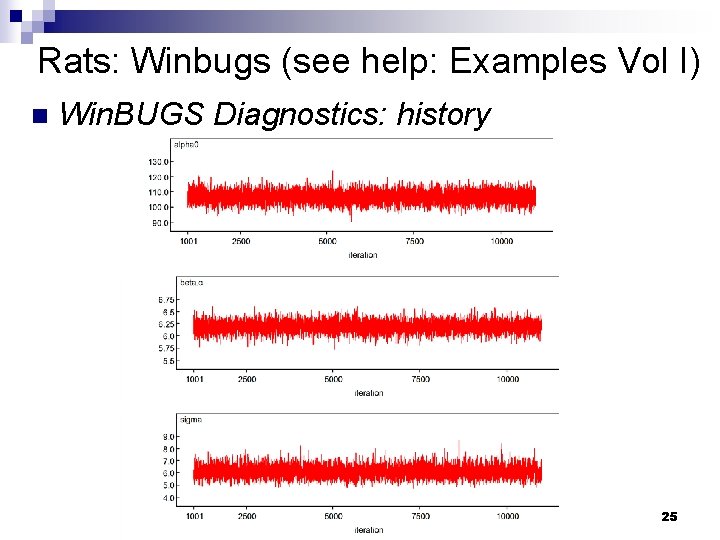
Rats: Winbugs (see help: Examples Vol I) n Win. BUGS Diagnostics: history 2005 Hopkins Epi-Biostat Summer Institute 25

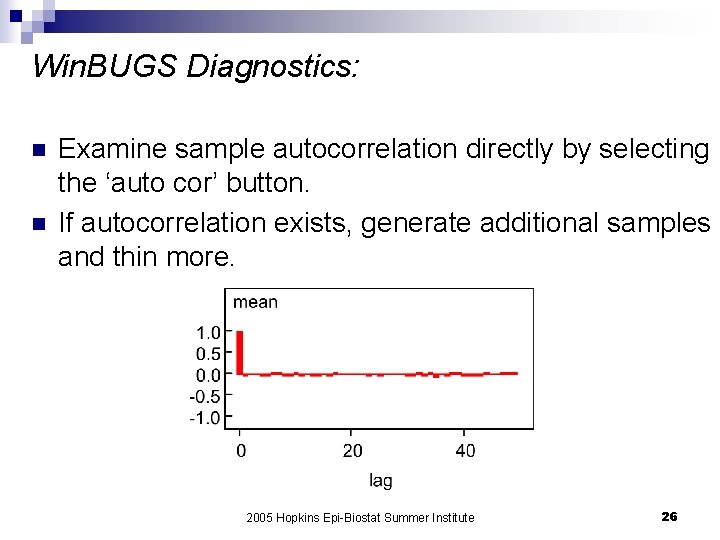
Win. BUGS Diagnostics: n n Examine sample autocorrelation directly by selecting the ‘auto cor’ button. If autocorrelation exists, generate additional samples and thin more. 2005 Hopkins Epi-Biostat Summer Institute 26

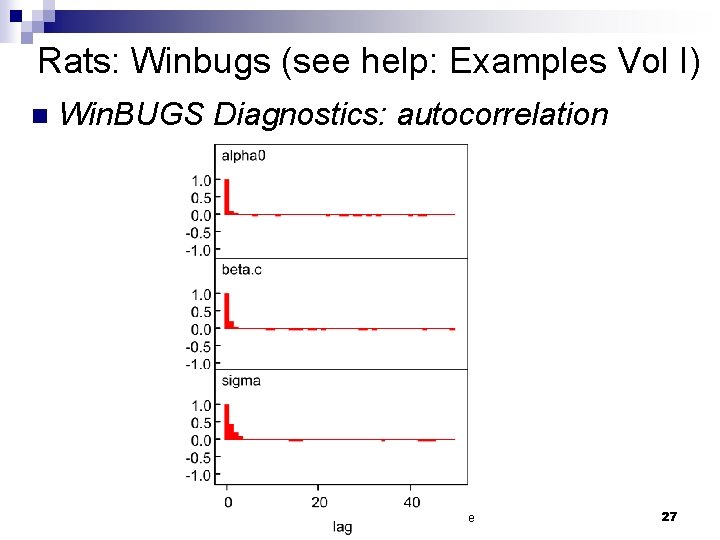
Rats: Winbugs (see help: Examples Vol I) n Win. BUGS Diagnostics: autocorrelation 2005 Hopkins Epi-Biostat Summer Institute 27

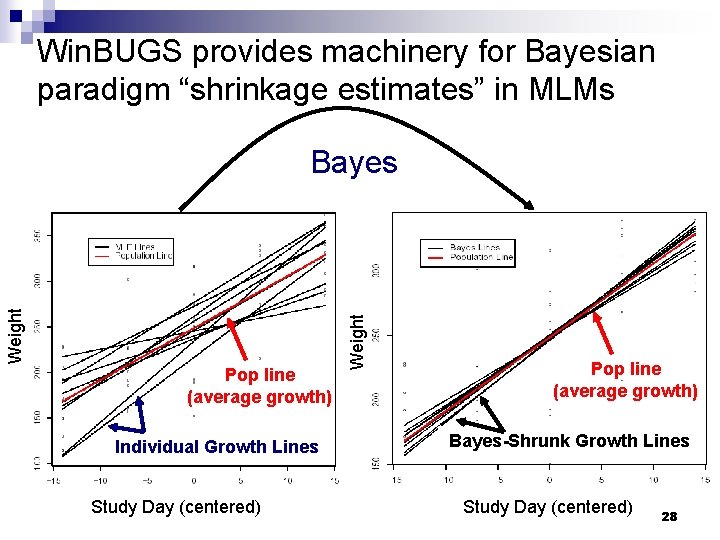
Win. BUGS provides machinery for Bayesian paradigm “shrinkage estimates” in MLMs Pop line (average growth) Individual Growth Lines Weight Bayes Pop line (average growth) Bayes-Shrunk Growth Lines Study Day (centered) 2005 Hopkins Epi-Biostat Summer Institute 28

School Test Scores Revisited 2005 Hopkins Epi-Biostat Summer Institute 29

Testing in Schools revisited n n Suppose we wanted to include covariate information in the school test scores example Student-level covariates Gender ¨ London Reading Test (LRT) score ¨ Verbal reasoning (VR) test category (1, 2 or 3) ¨ n School -level covariates Gender intake (all girls, all boys or mixed) ¨ Religious denomination (Church of England, Roman Catholic, State school or other) ¨ 2005 Hopkins Epi-Biostat Summer Institute 30

Testing in Schools revisited n Model n Wow! Can YOU fit this model? n Yes you can! n See Win. BUGS>help>Examples Vol II for data, code, results, etc. n More Importantly: Do you understand this model? 2005 Hopkins Epi-Biostat Summer Institute 31

Bayesian Concepts n Frequentist: Parameters are “the truth” n Bayesian: Parameters have a distribution n “Borrow Strength” from other observations n “Shrink Estimates” towards overall averages n Compromise between model & data n Incorporate prior/other information in estimates n Account for other sources of uncertainty n Posterior Likelihood * Prior 2005 Hopkins Epi-Biostat Summer Institute 32