Module 14 Polynomials and Operations Learning goal Students












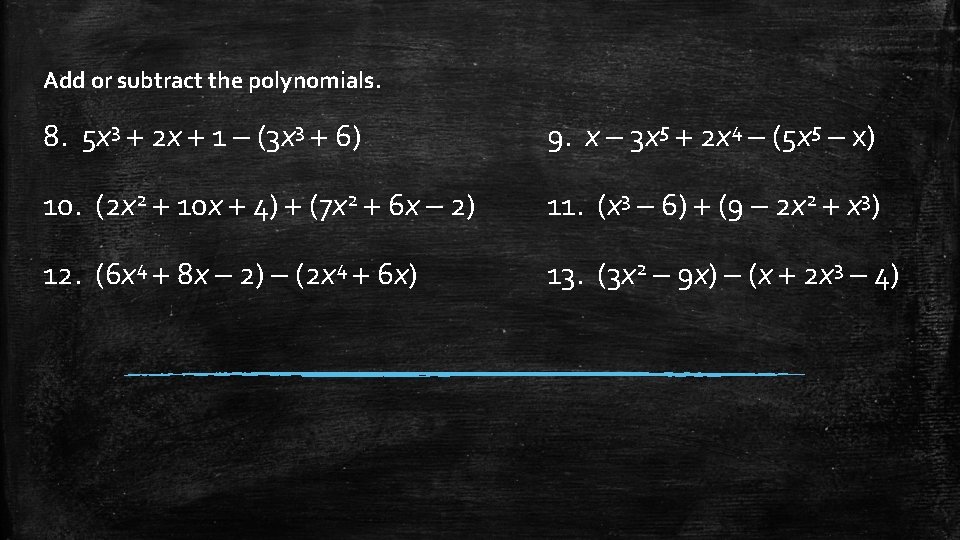



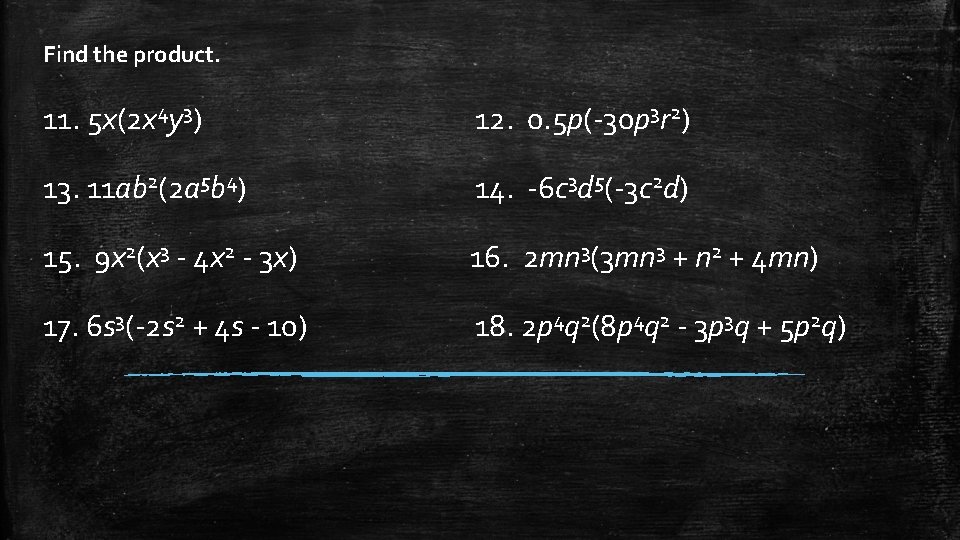



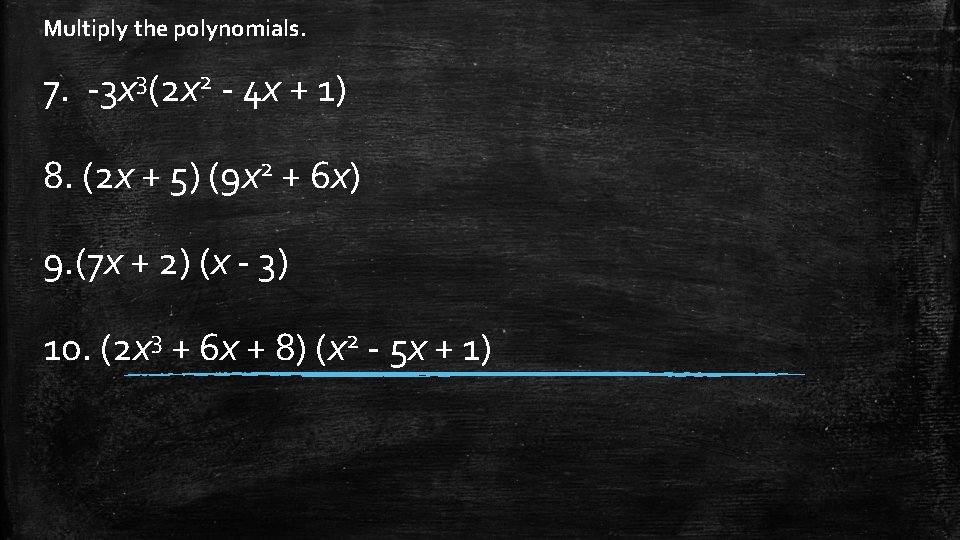

- Slides: 25

Module 14 Polynomials and Operations Learning goal: Students will be able to perform arithmetic operations on polynomials and find factors and zeroes of polynomials.

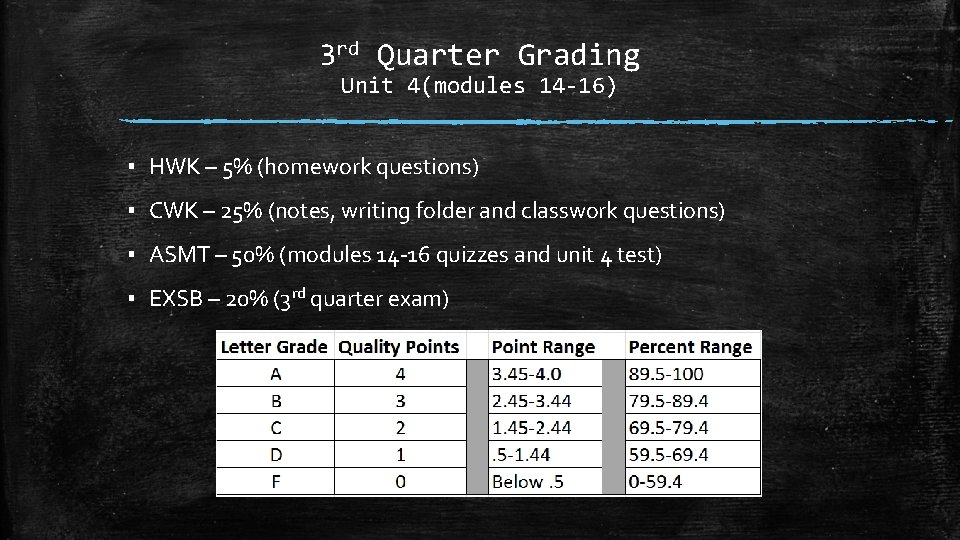
3 rd Quarter Grading Unit 4(modules 14 -16) ▪ HWK – 5% (homework questions) ▪ CWK – 25% (notes, writing folder and classwork questions) ▪ ASMT – 50% (modules 14 -16 quizzes and unit 4 test) ▪ EXSB – 20% (3 rd quarter exam)

Cornell Notes

Example

Polynomials and Operations You should be able to: You will learn how to: ▪ evaluate expressions ▪ classify polynomials ▪ simplify expressions ▪ evaluate polynomial expressions ▪ write expressions ▪ add, subtract, and multiply polynomials ▪ represent functions ▪ factor polynomials ▪ solve quadratic polynomial expressions

14. 1 Understanding Polynomials Opening activity - Explore p 485 Reading assignment p 486 -488 ▪ Learning goal: Students will be able to perform arithmetic operations on polynomials and find factors and zeroes of polynomials. ▪ Essential question: What are polynomial expressions and how do you simplify them?

14. 1 Understanding Polynomials 1. What is different about polynomials and monomials? 2. Describe how to find the degree of a monomial. 3. Describe how to find the degree of a polynomial.

14. 1 Understanding Polynomials 4. How many terms are in a trinomial? a monomial? 5. Why does 5 xy 3 have a degree of 4? 6. Classify 4 n 3 + 6 by degree. by number of terms.

Use the polynomial 8 g + 1 – 4 g 2 to complete the following. 7. Write the polynomial in standard form. 8. What is the leading coefficient? 9. What is the degree of the polynomial? 10. Classify the polynomial by number of terms. 11. Classify the polynomial by degree.

14. 1 Understanding Polynomials Homework Questions p 490 -492 #12 -20 evens, 28, 30, 31 Writing Folder p 489 #10

14. 2 Adding and Subtracting Polynomials Opening activity – Explore p 493 Reading assignment p 494 -497 ▪ Learning goal: Students will be able to perform arithmetic operations on polynomials and find factors and zeroes of polynomials. ▪ Essential question: How do you add and subtract polynomials?

14. 2 Adding and Subtracting Polynomials 1. If m 3 is represented by a cube with side length m, explain how to represent m 2. 2. When subtracting one polynomial from another polynomial, what must you do first? 3. What property allows you to rearrange terms?

14. 2 Adding and Subtracting Polynomials 4. What is being distributed in the linear expression on the left? 5. What is being distributed in the polynomial subtraction on the right? 6. Identify the sets of like terms that were combined in the expression on the left. 7. Identify the sets of like terms that were combined in the polynomial subtraction on the right.
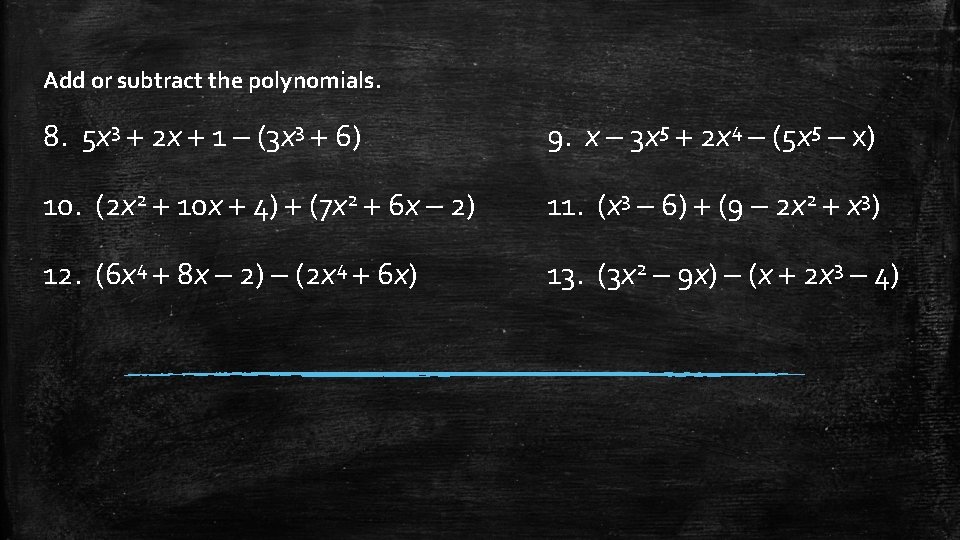
Add or subtract the polynomials. 8. 5 x 3 2 x 1 (3 x 3 6) 9. x 3 x 5 2 x 4 (5 x 5 x) 10. (2 x 2 10 x 4) (7 x 2 6 x 2) 11. (x 3 6) (9 2 x 2 x 3) 12. (6 x 4 8 x 2) (2 x 4 6 x) 13. (3 x 2 9 x) (x 2 x 3 4)

14. 2 Understanding Polynomials Homework Problems p 499 -500 #15 -20 evens, 23, 25, 26 Writing Folder p 498 #8

14. 3 Multiplying Polynomials and Monomials Opening activity – Explore p 501 Reading assignment p 501 -505 ▪ Learning goal: Students will be able to perform arithmetic operations on polynomials and find factors and zeroes of polynomials. ▪ Essential question: How can you multiply polynomials by monomials?

14. 3 Multiplying Polynomials and Monomials 1. In Problem 2, why does the subtraction change to addition? 2. Why did the exponents in Problem 2 remain the same? 3. In Problem 1, how would multiplying by -3 m 2 n 3 make the answer different? 4. Find the product of 3 x 2 and -4 xy 3 + 12 x 8 -2 y 4?

14. 3 Multiplying Polynomials and Monomials Using the compare and contrast chart, label the expressions in Exercises 5 -10 as monomials or polynomials. 5. 3 nm 5 6. 5 rt – 2 r 2 7. -3 xy 3 + 4 x 8. 5 – 6 h 2 g 9. 4 m 10. 6 e 4 – 2 e
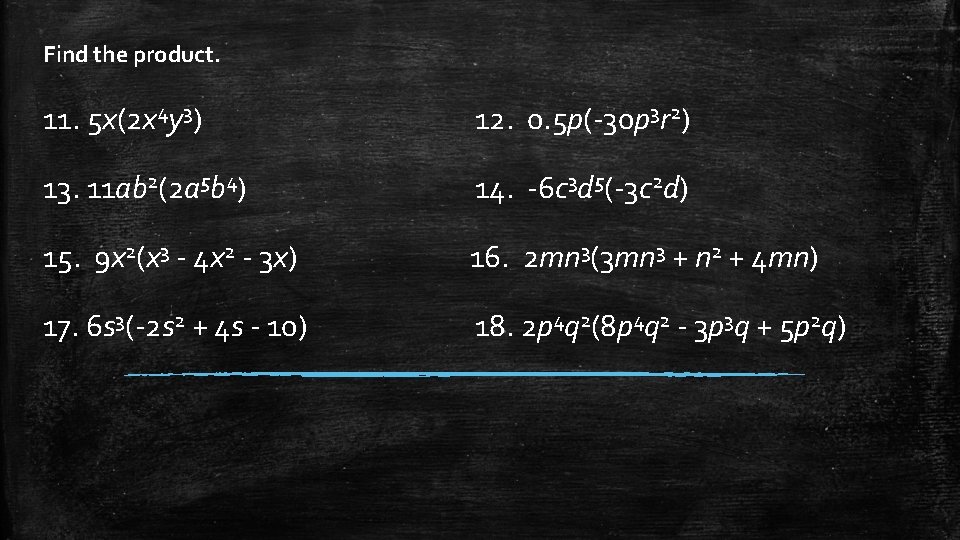
Find the product. 11. 5 x(2 x 4 y 3) 12. 0. 5 p(-30 p 3 r 2) 13. 11 ab 2(2 a 5 b 4) 14. -6 c 3 d 5(-3 c 2 d) 15. 9 x 2(x 3 - 4 x 2 - 3 x) 16. 2 mn 3(3 mn 3 + n 2 + 4 mn) 17. 6 s 3(-2 s 2 + 4 s - 10) 18. 2 p 4 q 2(8 p 4 q 2 - 3 p 3 q + 5 p 2 q)

14. 3 Multiplying Polynomials and Monomials Homework Problems p 507 -508 #10 -26 evens, 27 Writing Folder p 506 #8

14. 4 Multiplying Polynomials Opening activity – Explore p 509 Reading assignment p 509 -513 ▪ Learning goal: Students will be able to perform arithmetic operations on polynomials and find factors and zeroes of polynomials. ▪ Essential question: How can you multiply binomials and polynomials?

14. 4 Multiplying Polynomials 1. What is the final product of the binomials in Problem 1? 2. How many x 2 tiles are in the model? x tiles? 1 tiles? 3. Create a model for the product (x + 4)2. x 4 x 4

14. 4 Multiplying Polynomials Use the procedure shown to answer each of the following. 4. Multiplication was used six times in step 1, How many times would it be used if two binomials were being multiplied? 5. In step 2, how do you know that 5 x 2 and -12 x 2 are like terms? 6. In step 3, how do you know the expression is completely simplified?
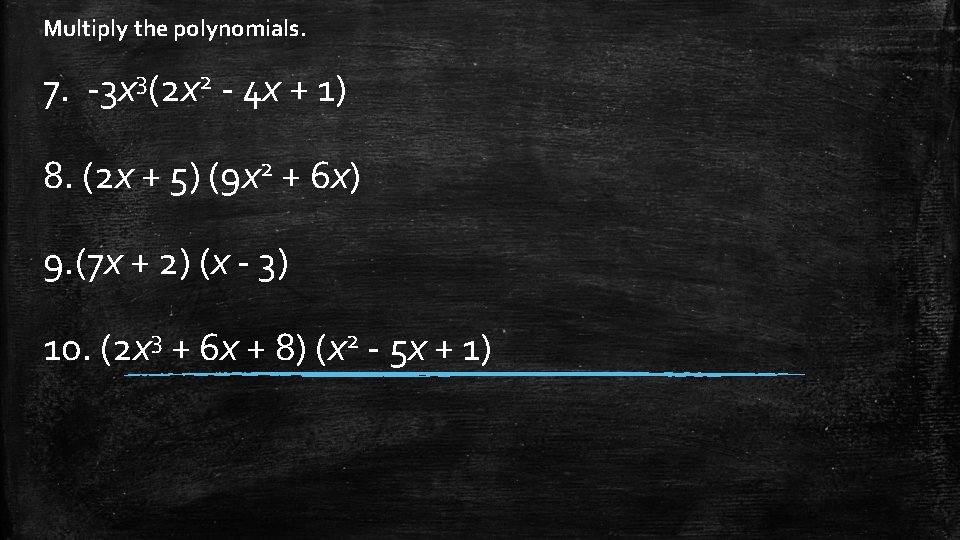
Multiply the polynomials. 7. -3 x 3(2 x 2 - 4 x + 1) 8. (2 x + 5) (9 x 2 + 6 x) 9. (7 x + 2) (x - 3) 10. (2 x 3 + 6 x + 8) (x 2 - 5 x + 1)

14. 4 Multiplying Polynomials Homework Problems p 515 -516 #12 -22 even, 23, 25 -27 Writing Folder p 514 #11