Module 10 COORDINATE PROOFS Using Distance and Slope

Module 10 – COORDINATE PROOFS Using Distance and Slope to prove facts about quadrilaterals and triangles. Today you will need: -Your Notes -Coordinate Practice Worksheet

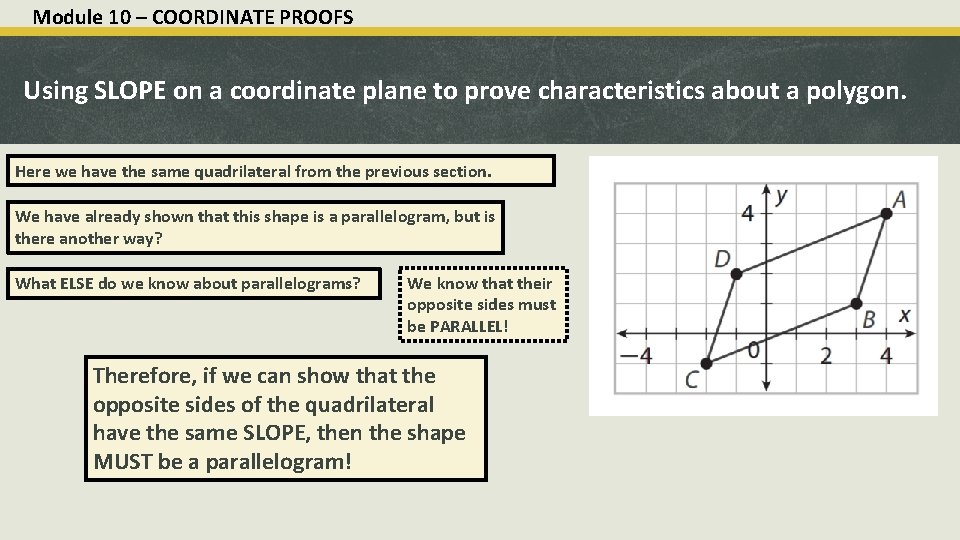
Module 10 – COORDINATE PROOFS Using SLOPE on a coordinate plane to prove characteristics about a polygon. Here we have the same quadrilateral from the previous section. We have already shown that this shape is a parallelogram, but is there another way? What ELSE do we know about parallelograms? We know that their opposite sides must be PARALLEL! Therefore, if we can show that the opposite sides of the quadrilateral have the same SLOPE, then the shape MUST be a parallelogram!

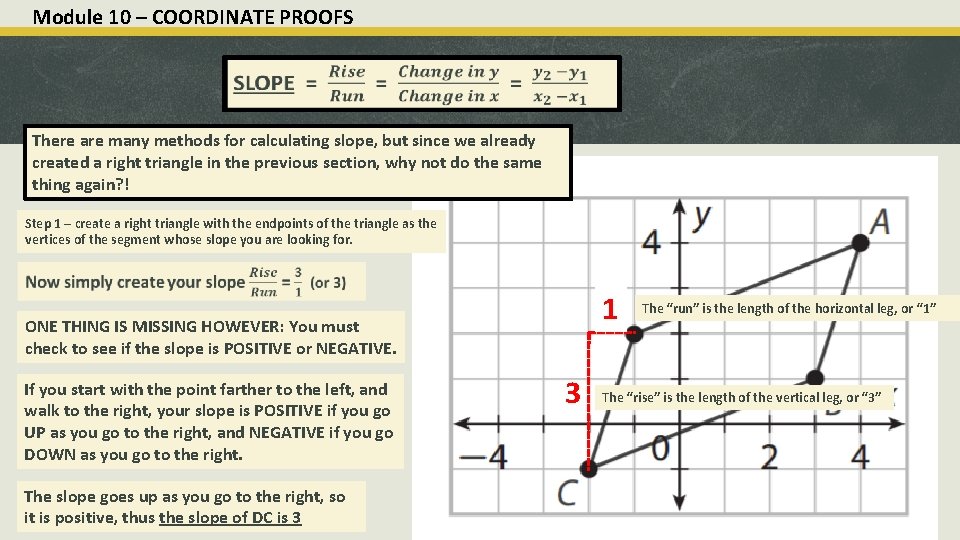
Module 10 – COORDINATE PROOFS There are many methods for calculating slope, but since we already created a right triangle in the previous section, why not do the same thing again? ! Step 1 – create a right triangle with the endpoints of the triangle as the vertices of the segment whose slope you are looking for. 1 ONE THING IS MISSING HOWEVER: You must check to see if the slope is POSITIVE or NEGATIVE. If you start with the point farther to the left, and walk to the right, your slope is POSITIVE if you go UP as you go to the right, and NEGATIVE if you go DOWN as you go to the right. The slope goes up as you go to the right, so it is positive, thus the slope of DC is 3 3 The “run” is the length of the horizontal leg, or “ 1” The “rise” is the length of the vertical leg, or “ 3”

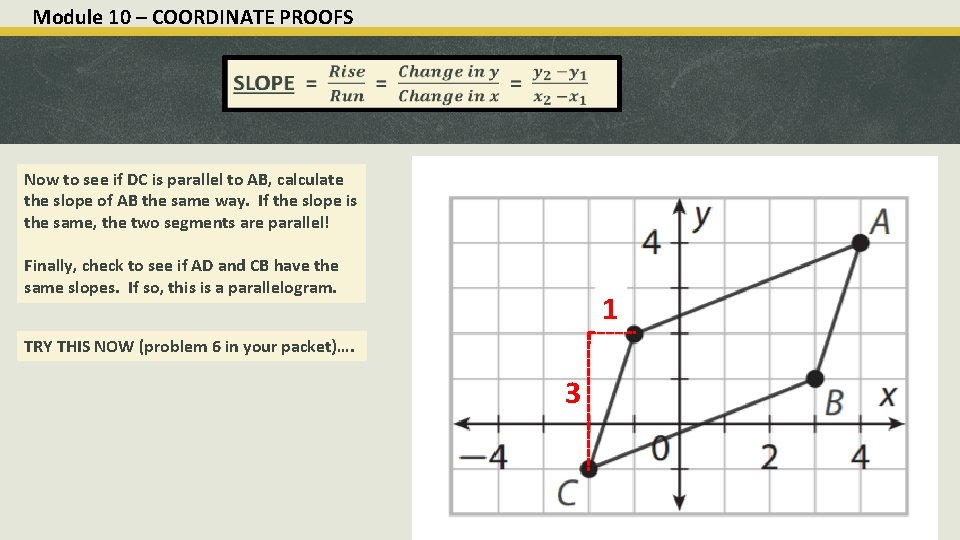
Module 10 – COORDINATE PROOFS Now to see if DC is parallel to AB, calculate the slope of AB the same way. If the slope is the same, the two segments are parallel! Finally, check to see if AD and CB have the same slopes. If so, this is a parallelogram. 1 TRY THIS NOW (problem 6 in your packet)…. 3

Module 10 – COORDINATE PROOFS Using PERPENDICULAR SLOPES on a coordinate plane to discover right angles. Here we have a polygon that appears to be a rectangle. What do we know about rectangles: We know that their opposite sides must be congruent and parallel (just like any parallelogram). But WHAT ELSE do we need to know to be sure this is a rectangle? We need to know that it has four right angles. We already know how to calculate the lengths of the sides of the quadrilateral to show that it is a parallelogram, and we can also calculate slope to show the very same thing, but we need to know a little bit more… we need to see that the slopes of the adjacent sides are PERPENDICULAR!

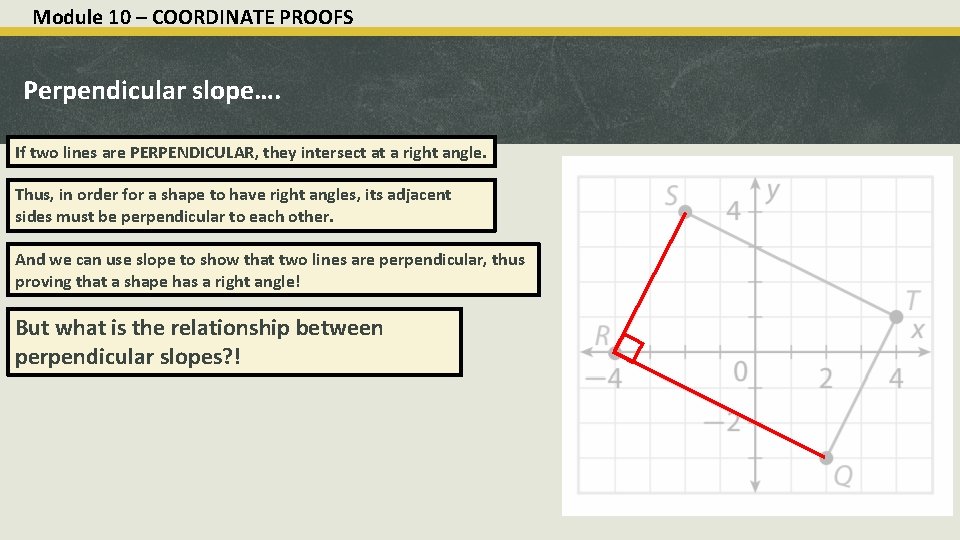
Module 10 – COORDINATE PROOFS Perpendicular slope…. If two lines are PERPENDICULAR, they intersect at a right angle. Thus, in order for a shape to have right angles, its adjacent sides must be perpendicular to each other. And we can use slope to show that two lines are perpendicular, thus proving that a shape has a right angle! But what is the relationship between perpendicular slopes? !

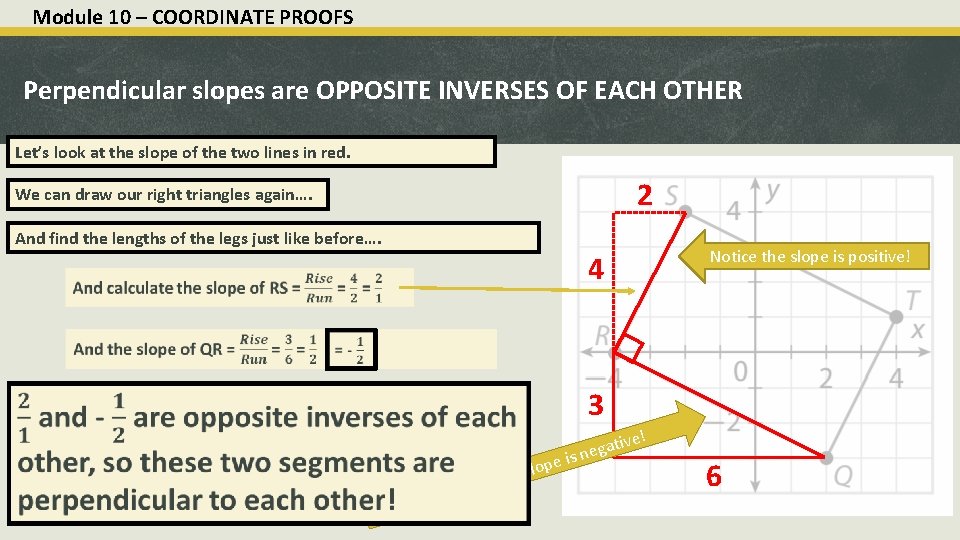
Module 10 – COORDINATE PROOFS Perpendicular slopes are OPPOSITE INVERSES OF EACH OTHER Let’s look at the slope of the two lines in red. 2 We can draw our right triangles again…. And find the lengths of the legs just like before…. 4 Notice the slope is positive! 3 ive! t a g s ne A otice n d n pe i o l s s thi 6

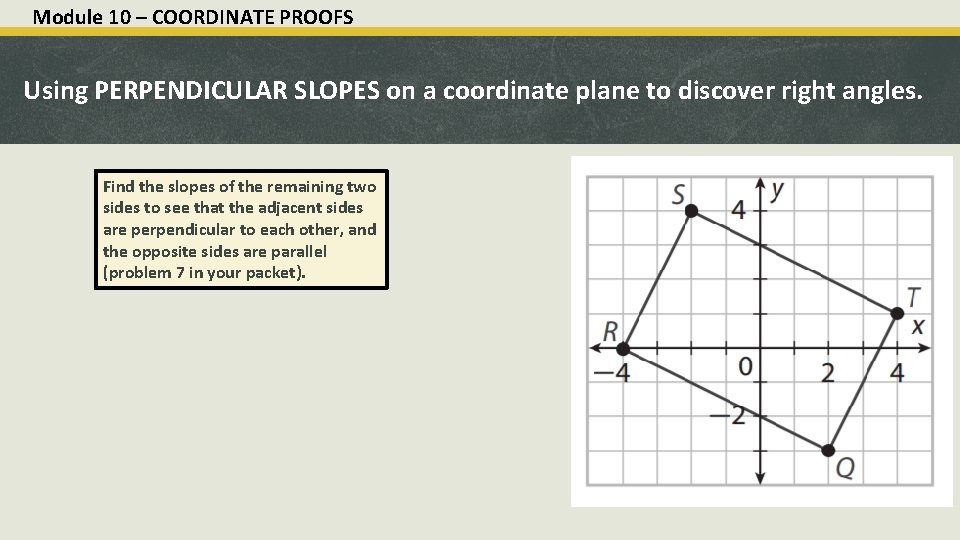
Module 10 – COORDINATE PROOFS Using PERPENDICULAR SLOPES on a coordinate plane to discover right angles. Find the slopes of the remaining two sides to see that the adjacent sides are perpendicular to each other, and the opposite sides are parallel (problem 7 in your packet).

Module 10 Classwork/Homework Problems Complete the remaining problems on pages 3 and 4 of the worksheet. Then do pages 501 -502, #’s 2 -7