Module 1 Quadratic Equations Inequalities and Functions Lesson

Module 1 Quadratic Equations, Inequalities and Functions Lesson 1 Quadratic Functions

LAS # 2: STANDARD Form of a Quadratic Function The function defined by the second degree equation f(x) = ax 2 + bx + c where a, b, and c are real numbers and a ≠ 0, is a quadratic function in x. This function can also be written as y = ax 2 + bx + c , where y = f(x). Example: a b c 1. y = 2 x 2 – 3 x - 10 2 -3 -10 2. y = 3 x 2 + 5 x 3 5 0 3. y = 4 x 2 - 7 4 0 -7 4. y = -5 x 2 – 3 x 2 -5 2 -3 2 0 5. y = x 2 1 0 0 Copyright © by Mr. Florben G. Mendoza 2

STANDARD FORM of a Quadratic Function f(x) = ax 2 + bx + c Example: Write the following equations in STANDARD FORM. 1. y – 12 = - 5 x + 3 x 2 2. y = (x + 5)2 – 2(x + 17) + 55 y = – 5 x + 3 x 2 + 12 y = x 2 + 10 x + 25 – y = 3 x 2 – 5 x + 12 y = x 2 + 8 x + 46 f (x) = 3 x 2 – 5 x + 12 f(x) = x 2 + 8 x + 46 3. y = 7 – (x – 3) (x + 3) y=7– (x 2 – y=7– x 2 + y = -x 2 + 16 2 x – 34 + 55 (a + b)2 = a 2 + 2 ab + b 2 9) (x + 5)2 = x 2 + 2(x)(5) + 52 9 (x + 5)2 = x 2 + 10 x + 25 or f(x) = -x 2 + 16 – 2(x + 17) = -2 x - 34 (a + b) ( a – b) = a 2 - b 2 (x – 3) (x + 3)= x 2 - 9 Copyright © by Mr. Florben G. Mendoza 3

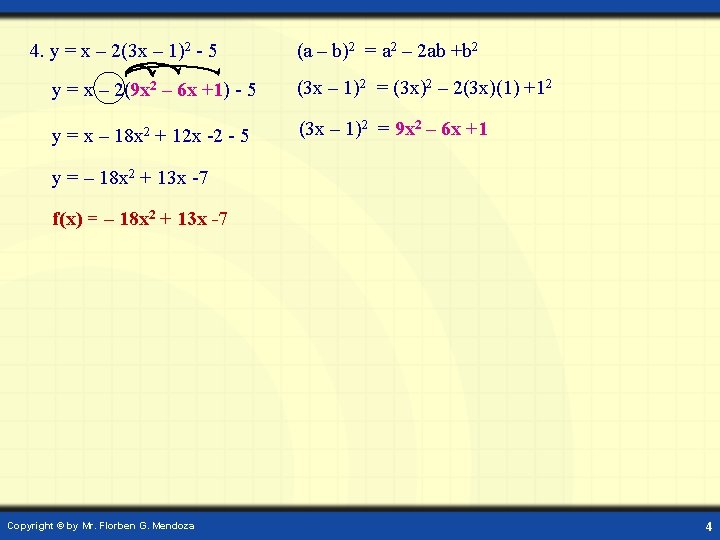
4. y = x – 2(3 x – 1)2 - 5 (a – b)2 = a 2 – 2 ab +b 2 y = x – 2(9 x 2 – 6 x +1) - 5 (3 x – 1)2 = (3 x)2 – 2(3 x)(1) +12 y = x – 18 x 2 + 12 x -2 - 5 (3 x – 1)2 = 9 x 2 – 6 x +1 y = – 18 x 2 + 13 x -7 f(x) = – 18 x 2 + 13 x -7 Copyright © by Mr. Florben G. Mendoza 4

Equal Differences Method Direction: Using the equal differences method, determine which of the following ordered pairs represent a quadratic function. 2) (-6, -7), (-4, -3), (-2, 1), (0, 5), (2, 9), (4, 13), (6, 17) 2 x f(x ) -6 -4 -7 -3 1) (-2, 4), (-1, 1), (0, 0), (1, 1), (2, 4) 1 1 1 -2 -1 0 1 2 y 4 1 0 1 4 -1 2 3 2 The ordered pairs represents a QUADRATIC FUNCTION Copyright © by Mr. Florben G. Mendoza -2 1 4 0 5 2 2 9 4 13 4 4 4 2 6 17 4 1 st Difference x -3 4 1 2 2 2 1 st NOT A QUADRATIC FUNCTION – LINEAR FUNCTION 3) (-4, -73), (-2, -13), (0, -1), (2, 11), (4, 71) 2 Difference 2 nd Difference x f(x ) -4 -2 0 -73 -1 60 2 11 12 12 -48 0 48 2 2 2 4 71 60 1 st Difference 48 48 2 nd Difference 3 rd Difference NOT A QUADRATIC FUNCTION – CUBIC FUNCTION 5

LAS # 2 Activity # 1 I. Write each of these quadratic function in general form, then identify the real numbers a, b, and c. General Form a b c 1. y – 5 = - 2 x + 4 x 2 2. y - 6 = (x + 3)2 – 2(x + 12) 3. y = 9 – (x – 4) (x + 4) 4. y + 5 = x – 3(2 x – 1)2 5. y = 5 + x(x - 3) + (x – 5) 2 Copyright © by Mr. Florben G. Mendoza 6

II. Using the equal differences method, name if the given ordered pairs represents the following: (a) Linear Function (c) Cubic Function (e) Quintic Function (b) Quadratic Function (d) Quartic Function 1. {(-6, -23), (-4, -17), (-2, -11), (0, -5), (2, 1), (4, 7), (6, 13)} 2. {(-5, 60), (-2, 15), (1, 6), (4, 33), (7, 96), (10, 195)} 3. {(-3, -243), (-2, -32), (-1, -1), (0, 0), (1, 1), (2, 32), (3, 243)} 4. {(-3, -49), (-2, -19), (-1, -5), (0, -1), (1, -1), (2, 1), (3, 11)} 5. {(-3, 83), (-2, 18), (-1, 3), (0, 2), (1, 3), (2, 18), (3, 83)} Copyright © by Mr. Florben G. Mendoza 7

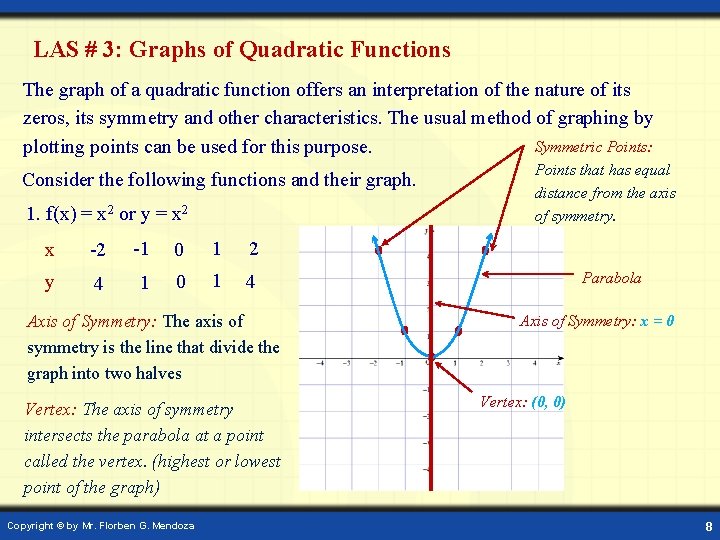
LAS # 3: Graphs of Quadratic Functions The graph of a quadratic function offers an interpretation of the nature of its zeros, its symmetry and other characteristics. The usual method of graphing by Symmetric Points: plotting points can be used for this purpose. Consider the following functions and their graph. 1. f(x) = x 2 or y = x 2 x -2 -1 0 1 2 y 4 1 0 1 4 Axis of Symmetry: The axis of symmetry is the line that divide the graph into two halves Vertex: The axis of symmetry intersects the parabola at a point called the vertex. (highest or lowest point of the graph) Copyright © by Mr. Florben G. Mendoza Points that has equal distance from the axis of symmetry. Parabola Axis of Symmetry: x = 0 Vertex: (0, 0) 8

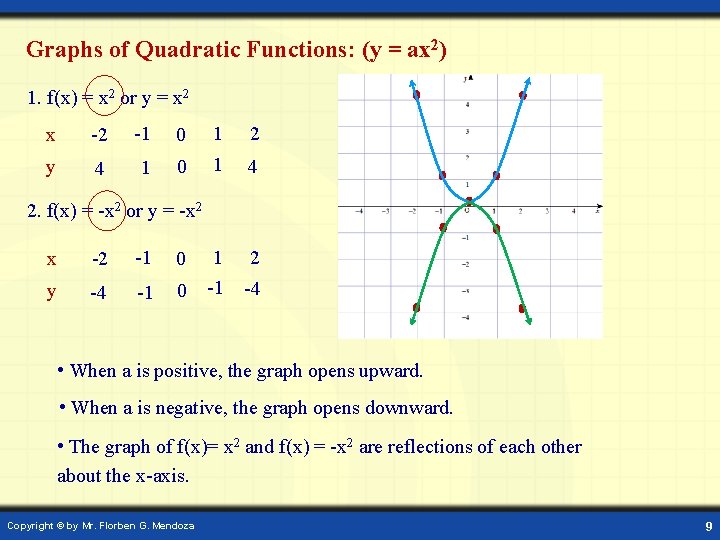
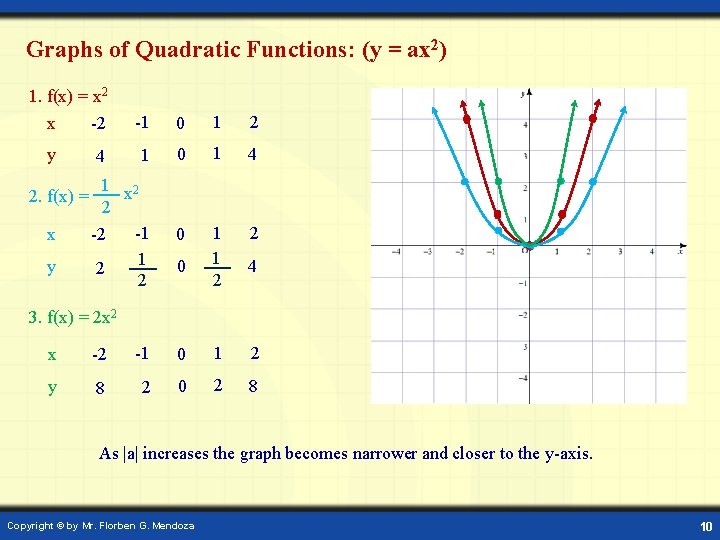
Graphs of Quadratic Functions: (y = ax 2) 1. f(x) = x 2 or y = x 2 x -2 -1 0 1 2 y 4 1 0 1 4 2 2. f(x) = -x 2 or y = -x 2 x -2 -1 0 1 y -4 -1 0 -1 -4 • When a is positive, the graph opens upward. • When a is negative, the graph opens downward. • The graph of f(x)= x 2 and f(x) = -x 2 are reflections of each other about the x-axis. Copyright © by Mr. Florben G. Mendoza 9

Graphs of Quadratic Functions: (y = ax 2) 1. f(x) = x 2 x -2 y 2. f(x) = x y -1 0 1 2 1 0 1 4 1 x 2 2 -1 -2 1 2 2 0 1 1 2 2 4 0 4 3. f(x) = 2 x 2 x -2 -1 0 1 2 y 8 2 0 2 8 As |a| increases the graph becomes narrower and closer to the y-axis. Copyright © by Mr. Florben G. Mendoza 10

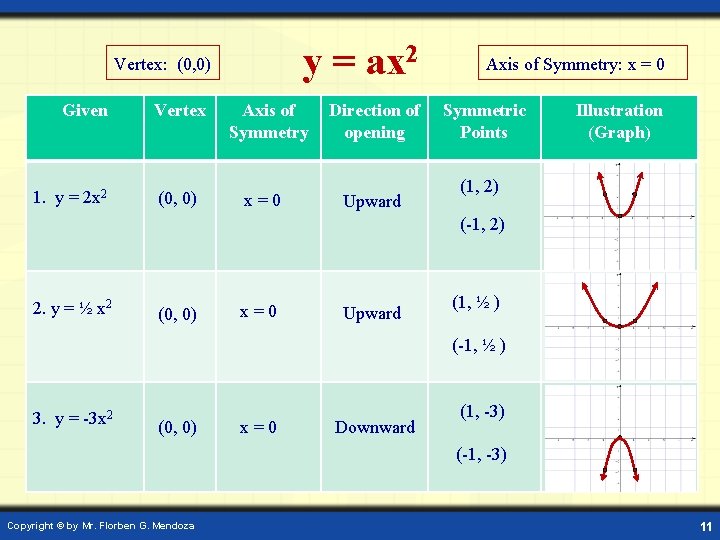
y = ax 2 Vertex: (0, 0) Given 1. y = 2 x 2 Vertex (0, 0) Axis of Symmetry x=0 Direction of opening Upward Axis of Symmetry: x = 0 Symmetric Points Illustration (Graph) (1, 2) (-1, 2) 2. y = ½ x 2 (0, 0) x=0 Upward (1, ½ ) (-1, ½ ) 3. y = -3 x 2 (0, 0) x=0 Downward (1, -3) (-1, -3) Copyright © by Mr. Florben G. Mendoza 11

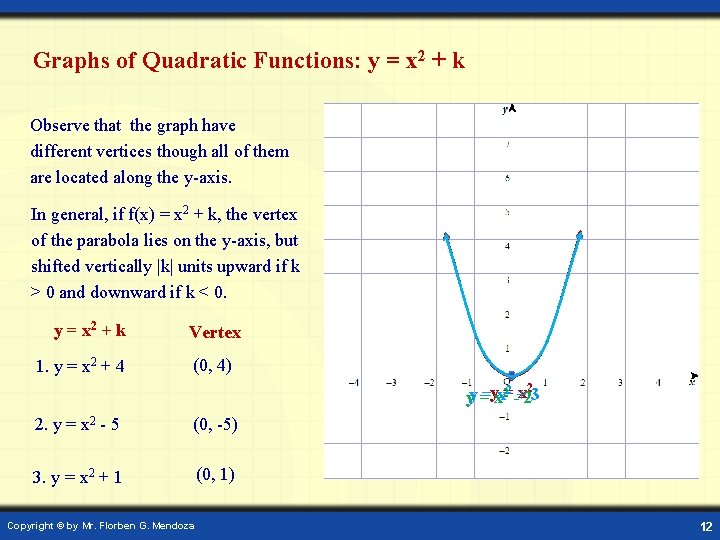
Graphs of Quadratic Functions: y = x 2 + k Observe that the graph have different vertices though all of them are located along the y-axis. In general, if f(x) = x 2 + k, the vertex of the parabola lies on the y-axis, but shifted vertically |k| units upward if k > 0 and downward if k < 0. y = x 2 + k 1. y = x 2 + 4 Vertex (0, 4) 2 yy ==yxx 2=2 -+x 23 2. y = x 2 - 5 (0, -5) 3. y = x 2 + 1 (0, 1) Copyright © by Mr. Florben G. Mendoza 12

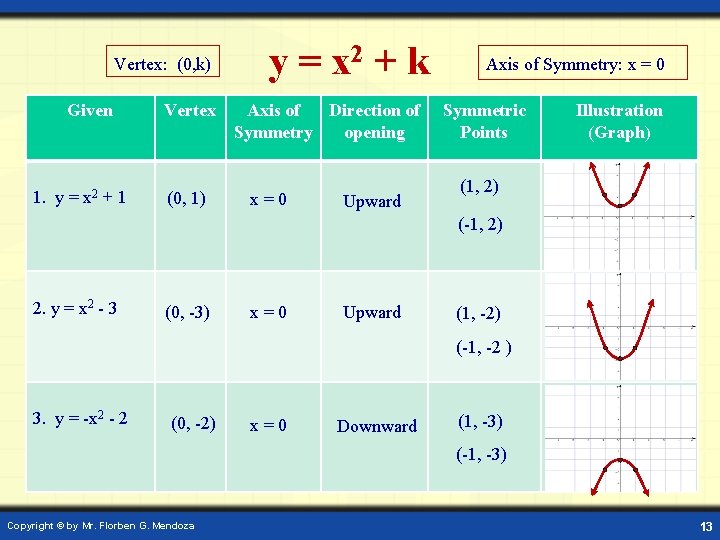
Vertex: (0, k) Given 1. y = x 2 + 1 Vertex (0, 1) y = x 2 + k Axis of Direction of Symmetry opening x=0 Upward Axis of Symmetry: x = 0 Symmetric Points Illustration (Graph) (1, 2) (-1, 2) 2. y = x 2 - 3 (0, -3) x=0 Upward (1, -2) (-1, -2 ) 3. y = -x 2 - 2 (0, -2) x=0 Downward (1, -3) (-1, -3) Copyright © by Mr. Florben G. Mendoza 13

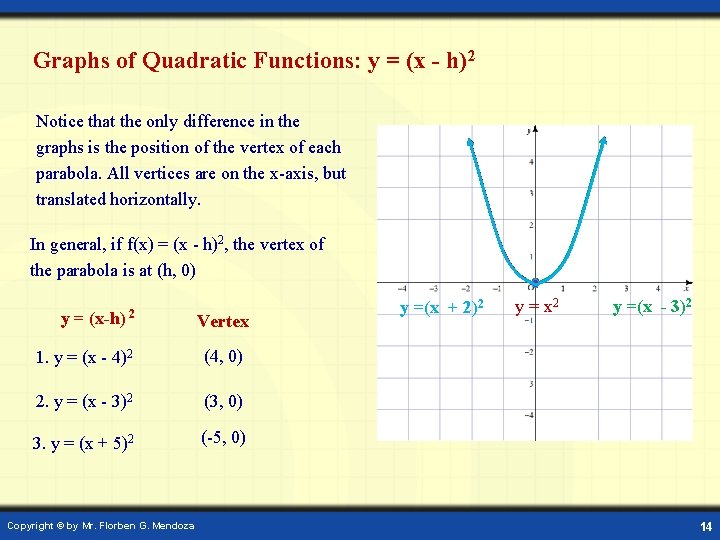
Graphs of Quadratic Functions: y = (x - h)2 Notice that the only difference in the graphs is the position of the vertex of each parabola. All vertices are on the x-axis, but translated horizontally. In general, if f(x) = (x - h)2, the vertex of the parabola is at (h, 0) y= (x-h) 2 Vertex 1. y = (x - 4)2 (4, 0) 2. y = (x - 3)2 (3, 0) 3. y = (x + 5)2 (-5, 0) Copyright © by Mr. Florben G. Mendoza y =(x + 2)2 y = x 2 y =(x - 3)2 14

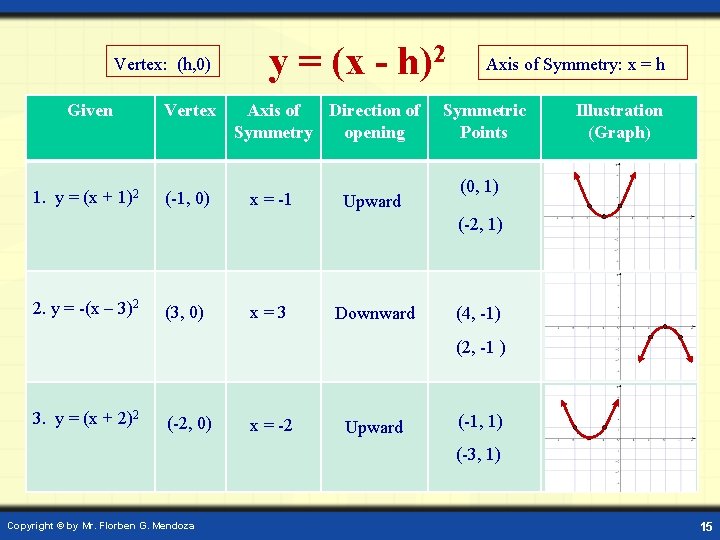
Vertex: (h, 0) Given Vertex 1. y = (x + 1)2 (-1, 0) y = (x - h)2 Axis of Direction of Symmetry opening x = -1 Upward Axis of Symmetry: x = h Symmetric Points Illustration (Graph) (0, 1) (-2, 1) 2. y = -(x – 3)2 (3, 0) x=3 Downward (4, -1) (2, -1 ) 3. y = (x + 2)2 (-2, 0) x = -2 Upward (-1, 1) (-3, 1) Copyright © by Mr. Florben G. Mendoza 15

Given 1. y = x 2 + 8 x + 16 Vertex Axis of Symmetry Direction of opening (-4, 0) x = -4 Upward Check: Symmetric Points Illustration (Graph) (-3, 1) (-5, 1) 16 = 4 x 2 = 8 y = (x + 4)2 Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 16

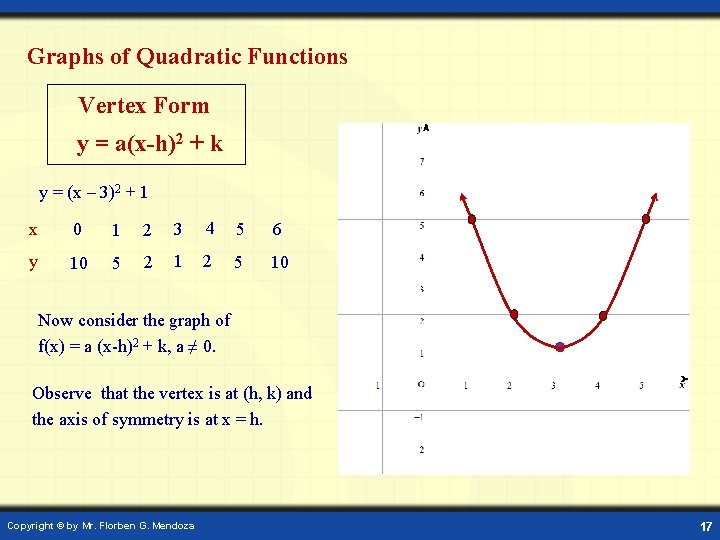
Graphs of Quadratic Functions Vertex Form y = a(x-h)2 + k y = (x – 3)2 + 1 x 0 1 2 3 4 5 6 y 10 5 2 1 2 5 10 Now consider the graph of f(x) = a (x-h)2 + k, a ≠ 0. Observe that the vertex is at (h, k) and the axis of symmetry is at x = h. Copyright © by Mr. Florben G. Mendoza 17

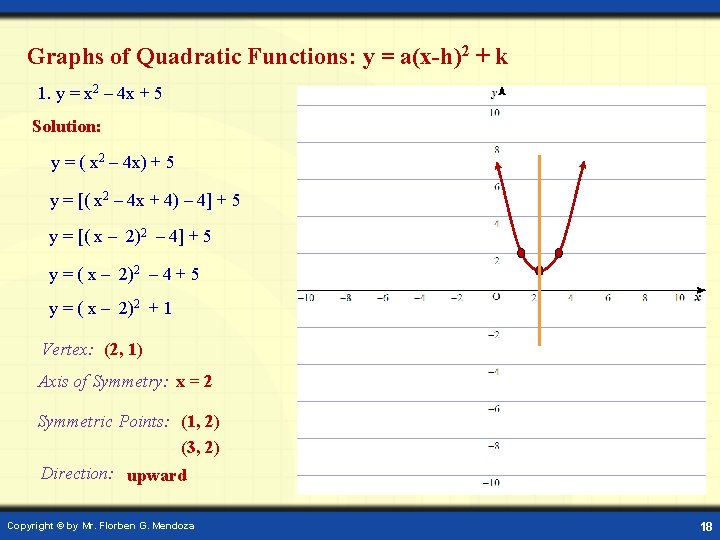
Graphs of Quadratic Functions: y = a(x-h)2 + k 1. y = x 2 – 4 x + 5 Solution: y = ( x 2 – 4 x) + 5 y = [( x 2 – 4 x + 4) – 4] + 5 y = [( x – 2)2 – 4] + 5 y = ( x – 2)2 – 4 + 5 y = ( x – 2)2 + 1 Vertex: (2, 1) Axis of Symmetry: x = 2 Symmetric Points: (1, 2) (3, 2) Direction: upward Copyright © by Mr. Florben G. Mendoza 18

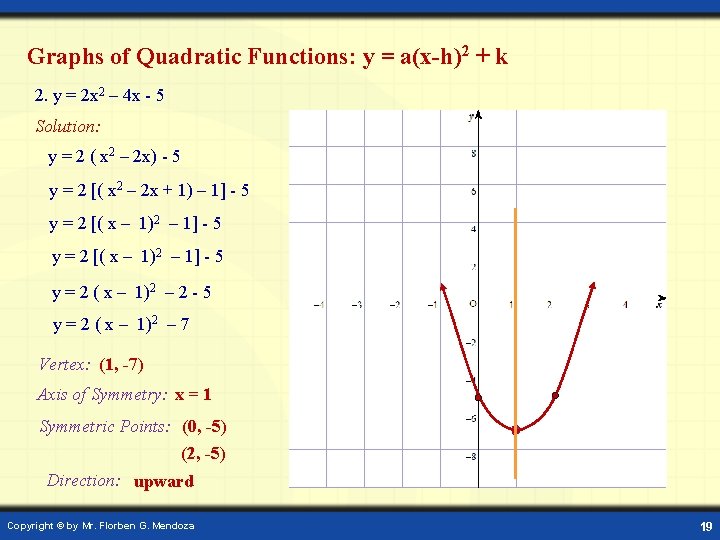
Graphs of Quadratic Functions: y = a(x-h)2 + k 2. y = 2 x 2 – 4 x - 5 Solution: y = 2 ( x 2 – 2 x) - 5 y = 2 [( x 2 – 2 x + 1) – 1] - 5 y = 2 [( x – 1)2 – 1] - 5 y = 2 ( x – 1)2 – 2 - 5 y = 2 ( x – 1)2 – 7 Vertex: (1, -7) Axis of Symmetry: x = 1 Symmetric Points: (0, -5) (2, -5) Direction: upward Copyright © by Mr. Florben G. Mendoza 19

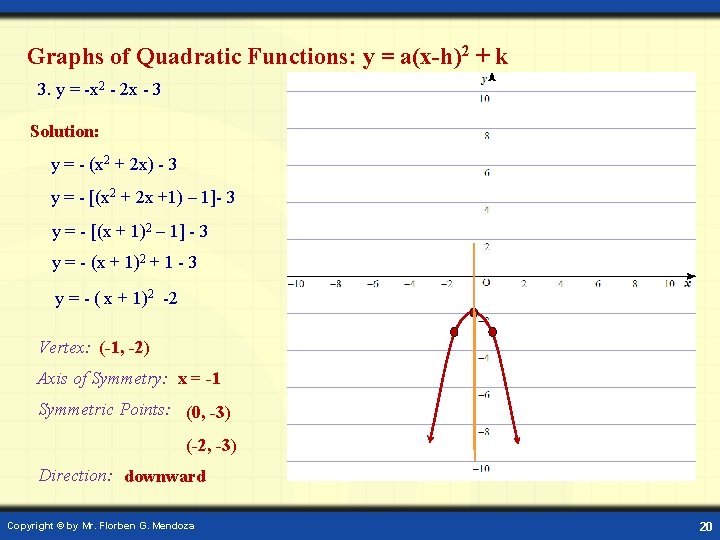
Graphs of Quadratic Functions: y = a(x-h)2 + k 3. y = -x 2 - 2 x - 3 Solution: y = - (x 2 + 2 x) - 3 y = - [(x 2 + 2 x +1) – 1]- 3 y = - [(x + 1)2 – 1] - 3 y = - (x + 1)2 + 1 - 3 y = - ( x + 1)2 -2 Vertex: (-1, -2) Axis of Symmetry: x = -1 Symmetric Points: (0, -3) (-2, -3) Direction: downward Copyright © by Mr. Florben G. Mendoza 20

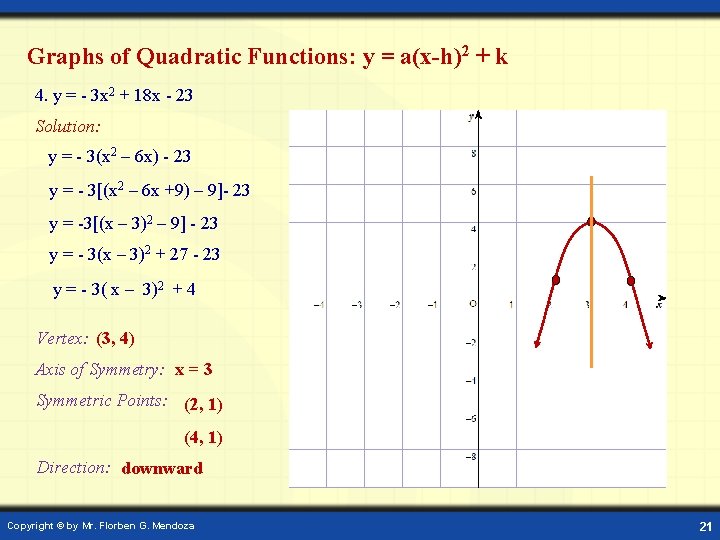
Graphs of Quadratic Functions: y = a(x-h)2 + k 4. y = - 3 x 2 + 18 x - 23 Solution: y = - 3(x 2 – 6 x) - 23 y = - 3[(x 2 – 6 x +9) – 9]- 23 y = -3[(x – 3)2 – 9] - 23 y = - 3(x – 3)2 + 27 - 23 y = - 3( x – 3)2 + 4 Vertex: (3, 4) Axis of Symmetry: x = 3 Symmetric Points: (2, 1) (4, 1) Direction: downward Copyright © by Mr. Florben G. Mendoza 21

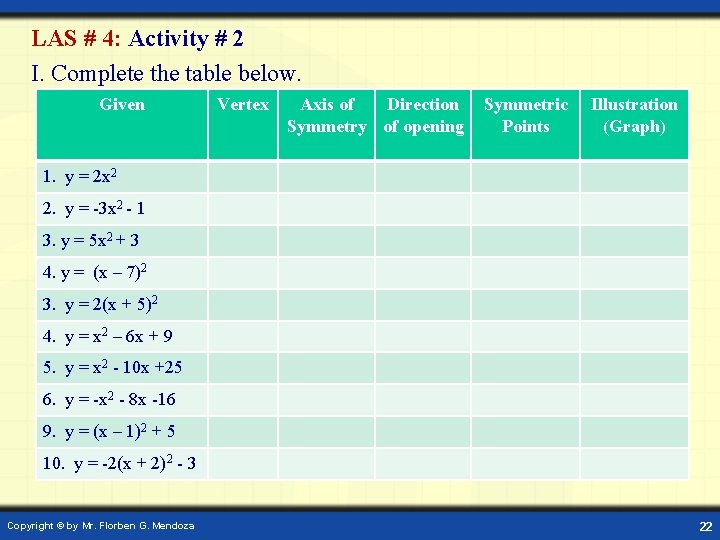
LAS # 4: Activity # 2 I. Complete the table below. Given Vertex Axis of Direction Symmetry of opening Symmetric Points Illustration (Graph) 1. y = 2 x 2 2. y = -3 x 2 - 1 3. y = 5 x 2 + 3 4. y = (x – 7)2 3. y = 2(x + 5)2 4. y = x 2 – 6 x + 9 5. y = x 2 - 10 x +25 6. y = -x 2 - 8 x -16 9. y = (x – 1)2 + 5 10. y = -2(x + 2)2 - 3 Copyright © by Mr. Florben G. Mendoza 22

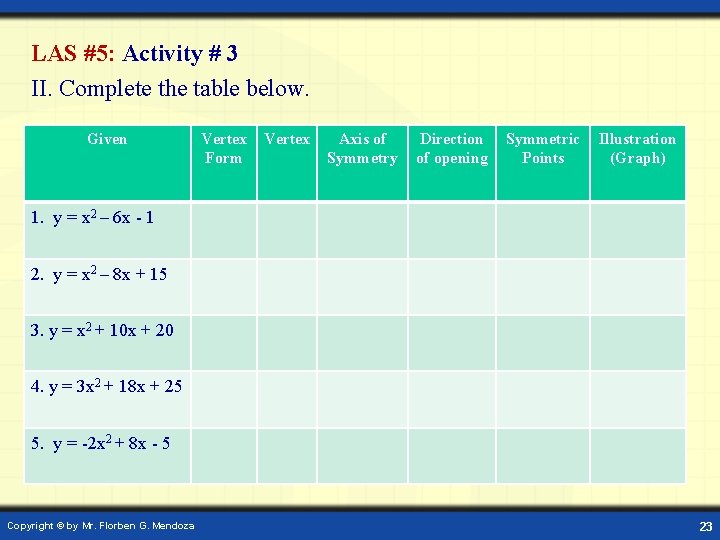
LAS #5: Activity # 3 II. Complete the table below. Given Vertex Form Vertex Axis of Symmetry Direction of opening Symmetric Points Illustration (Graph) 1. y = x 2 – 6 x - 1 2. y = x 2 – 8 x + 15 3. y = x 2 + 10 x + 20 4. y = 3 x 2 + 18 x + 25 5. y = -2 x 2 + 8 x - 5 Copyright © by Mr. Florben G. Mendoza 23