Modulation Index and Percent of Modulation n Used

Modulation Index and Percent of Modulation n Used to describe the amount of amplitude change (modulation) present in an AM waveform. Percentage modulation (%m) is simply the modulation index (m) stated as a percentage. More specifically, percent modulation gives the percentage change in the amplitude of the output wave when the carrier is acted on by a modulating signal. 1

Cont’d… n Mathematically, the modulation index is m = modulation index Em = peak change in the amplitude output waveform voltage (sum of voltages from upper and lower side frequencies) Ec = peak amplitude of the unmodulated carrier voltage n And the percentage of modulation index is 2

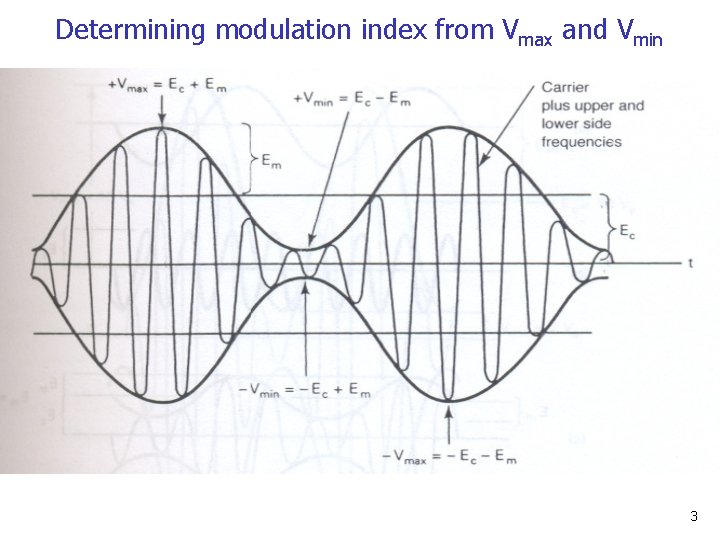
Determining modulation index from Vmax and Vmin 3

Cont’d… n n If the modulating signal is a pure, single-freq sine wave and the process is symmetrical then the modulation index can be derived as follows: Therefore, 4

Cont’d… n n Since the peak change of modulated output wave Em is the sum of the usf and lsf voltages hence, Then Eusf = peak amplitude of the upperside frequency (volts) Elsf = peak amplitude of the lower side frequency (volts) 5

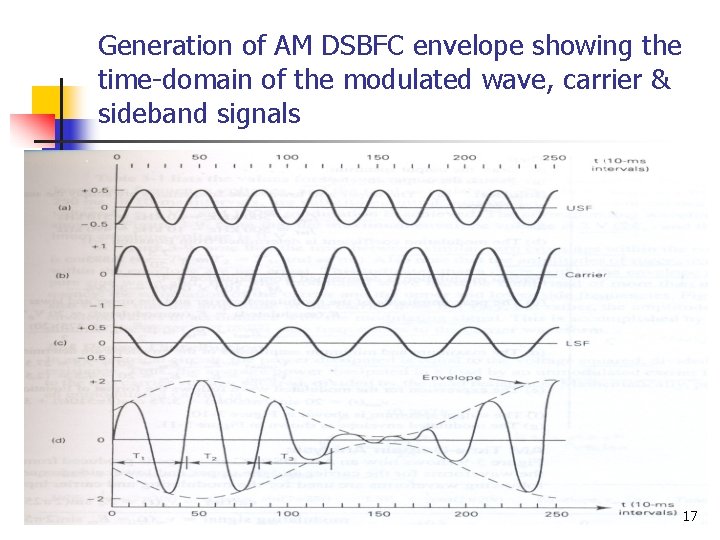
Cont’d… n From the modulated wave displayed in the previous slide, the maximum and minimum values of the envelope occurs at +Vmax = Ec + Eusb + Elsb +Vmin = Ec – Eusb – Elsb -Vmax = -Ec - Eusb - Elsb -Vmin = -Ec + Eusb + Elsb Note that Em = Eusb+ Elsb 6

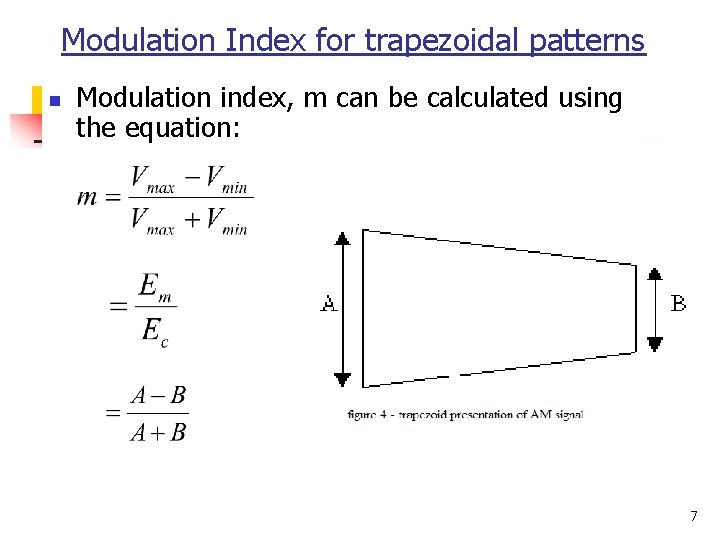
Modulation Index for trapezoidal patterns n Modulation index, m can be calculated using the equation: 7

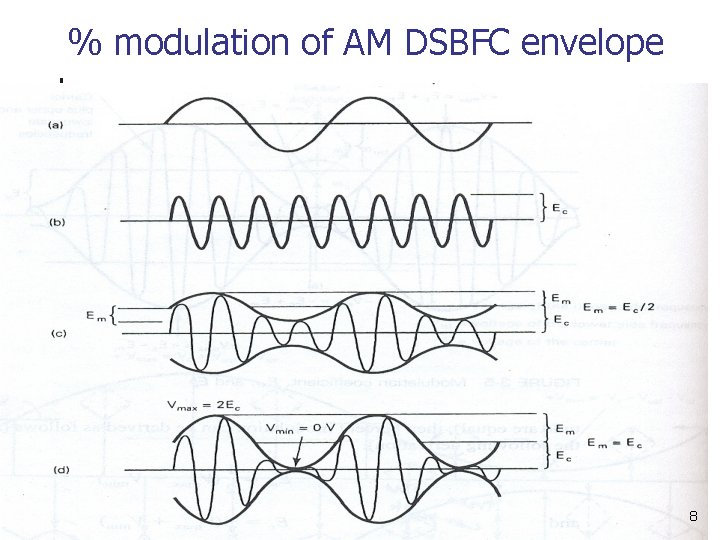
% modulation of AM DSBFC envelope 8

Cont’d… n n n For proper AM operation, Ec > Em means that 0≤ m ≤ 1. If Ec < Em means that m > 1 leads to severe distortion of the modulate wave. If Ec = Em the percentage of modulation index goes to 100%, means the maximum information signal is transmitted. In this case, Vmax = 2 Ec and Vmin = 0. 9

Example 2 n Suppose that Vmax value read from the graticule on an oscilloscope screen is 4. 6 divisions and Vmin is 0. 7 divisions. Calculate the modulation index and percentage of modulation. 10

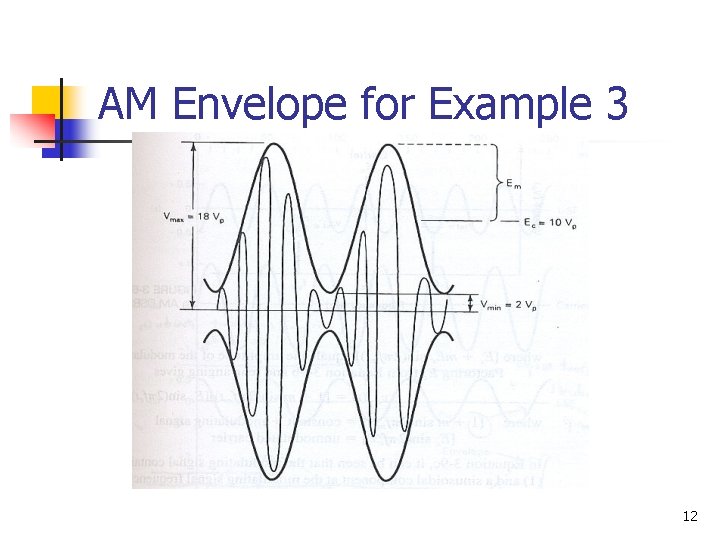
Example 3 n a) b) c) d) e) For the AM waveform shown in Figure below, determine Peak amplitude of the upper and lower side frequencies. Peak amplitude of the unmodulated carrier. Peak change in the amplitude of the envelope. Modulation index. Percent modulation. 11

AM Envelope for Example 3 12

The Mathematical Representation and Analysis of AM n n Representing both the modulating signal Vm(t) and the carrier signal Vc(t) in trigonometric functions. The AM DSBFC modulator must be able to produce mathematical multiplication of these two analog signals 13

Cont’d… n Substituting Vm = m. Vc gives: Constant + mod. signal Unmodulated carrier 14

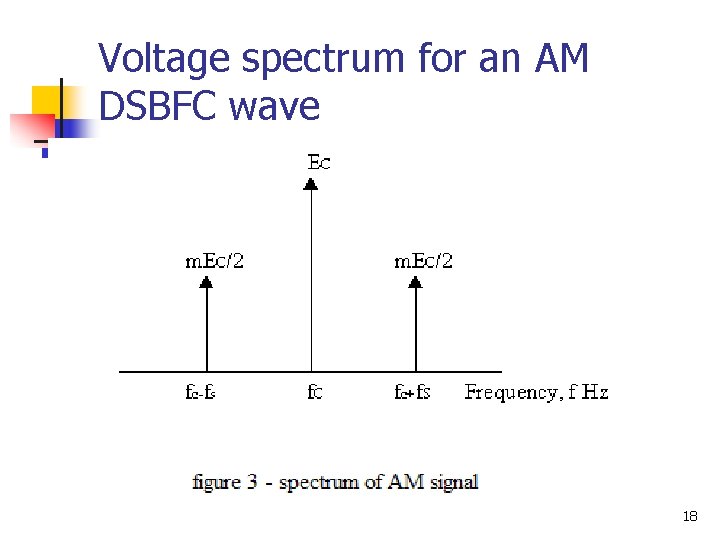
Cont’d… n The constant in the first term produces the carrier freq while the sinusoidal component in the first term produces side bands frequencies Carrier frequency signal (volts) Upper side frequency signal (volts) Lower side frequency signal (volts) 15

Cont’d… n n n From the equation it is obvious that the amplitude of the carrier is unaffected by the modulation process. The amplitude of side frequencies depends on both the carrier amplitude and modulation index. At 100% modulation the amplitudes of side frequencies are each equal to onehalf the amplitude of the carrier. 16

Generation of AM DSBFC envelope showing the time-domain of the modulated wave, carrier & sideband signals 17

Voltage spectrum for an AM DSBFC wave 18

Example 4 n a) b) c) d) e) f) g) One input to a conventional AM modulator is a 500 k. Hz carrier with an amplitude of 20 Vp. The second input is a 10 -k. Hz modulating signal that is of sufficient amplitude to cause a change in the output wave of ± 7. 5 Vp. Determine Upper and lower side frequencies. Modulation index and percentage modulation. Peak amplitude of the modulated carrier and the upper and lower side frequency voltages. Maximum and minimum amplitudes of the envelope. Mathematical expression for the modulated wave. Draw the output spectrum. Sketch the output envelope. 19

AM Power Distribution n n In any electrical circuit, the power dissipated is equal to the voltage squared (rms) divided by the resistance. Mathematically power in unmodulated carrier is Pc = carrier power (watts) Vc = peak carrier voltage (volts) R = load resistance i. e antenna (ohms) 20

Cont’d n n The upper and lower sideband powers will be Rearranging in terms of Pc, 21

Cont’d… n The total power in an AM wave is n Substituting the sidebands powers in terms of PC yields n Since carrier power in modulated wave is the same as unmodulated wave, obviously power of the carrier is unaffected by modulation process. 22

Power spectrum for AM DSBFC wave with a single-frequency modulating signal 23

Cont’d… n n n With 100% modulation the maximum power in both sidebands equals to one-half the carrier power. One of the most significant disadvantage of AM DSBFC is with m = 1, the efficiency of transmission is only 33. 3% of the total transmitted signal. The rest, wasted in the carrier which brings no information signal. The advantage of DSBFC is the use of relatively simple, inexpensive demodulator circuits in the receiver. 24

Example 5 n a) b) c) d) For an AM DSCFC wave with a peak unmodulated carrier voltage Vc = 10 Vp, a load resistor of RL = 10 and m = 1, determine Powers of the carrier and the upper and lower sidebands. Total sideband power. Total power of the modulated wave. Draw the power spectrum. 25

Transmitter Efficiency Transmitter efficiency, = תּ average power from sideband/total power absorbed. = m²/ ( 2+m² ) 26

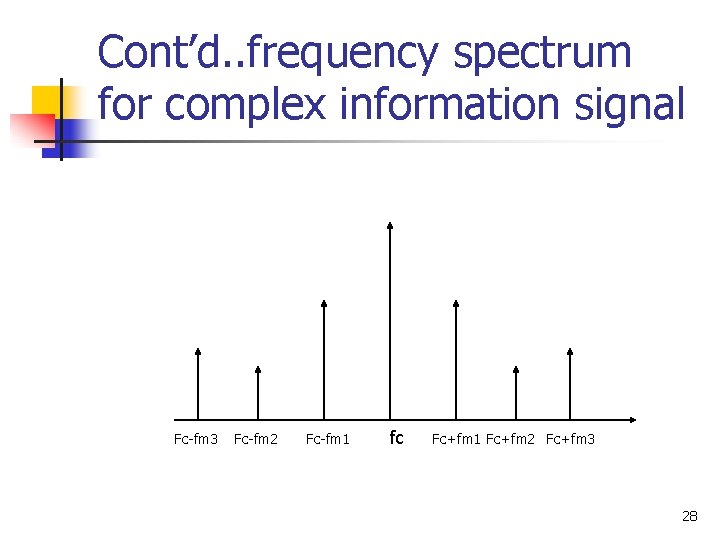
Modulation by a complex information signal n n Previous examples are all using a single frequency modulation signal. In practice, however, modulating signal is very often a complex waveform made up from many sine waves with different amplitudes and frequencies. Example: if a modulating signal contains three frequencies(f m 1, fm 2, fm 3), the modulated signal will contain the carrier and three sets of side frequencies, spaced symmetrically about the carrier: 27

Cont’d. . frequency spectrum for complex information signal Fc-fm 3 Fc-fm 2 Fc-fm 1 fc Fc+fm 1 Fc+fm 2 Fc+fm 3 28

Cont’d. . modulation index for complex information signal n When several frequencies simultaneously amplitude modulate a carrier, the combined coefficient of modulation is defined as: mt=total modulation index/coefficient of modulation m 1, m 2, m 3, mn= modulation index/coefficient of modulation for input 1, 2 , 3 , n 29

Cont’d. . Power calculation for complex information signal n The combined coefficient of modulation can be used to determine the total sideband power and transmitted power, using: 30

Example 6 n a) b) c) For an AM DSBFC transmitter with an unmodulated carrier power, Pc= 100 W that is modulated simultaneously by three modulating signals, with coefficients of modulation m 1=0. 2, m 2= 0. 4, m 3=0. 5, determine: Total coefficient of modulation Upper and lower sideband power Total transmitted power 31

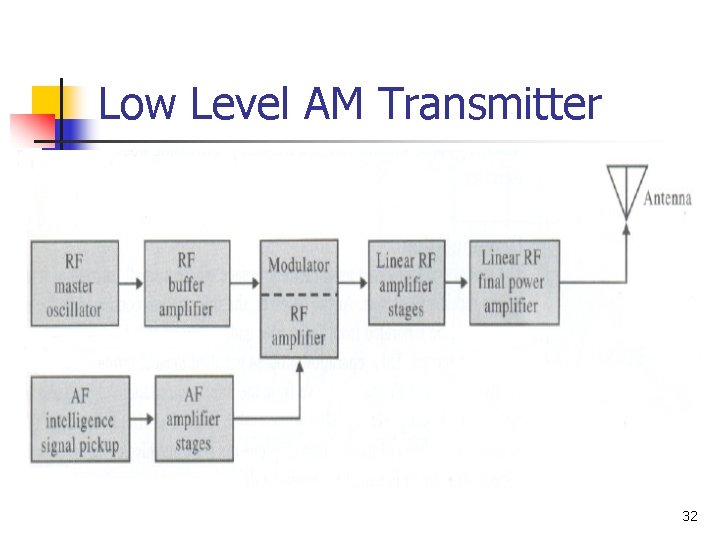
Low Level AM Transmitter 32

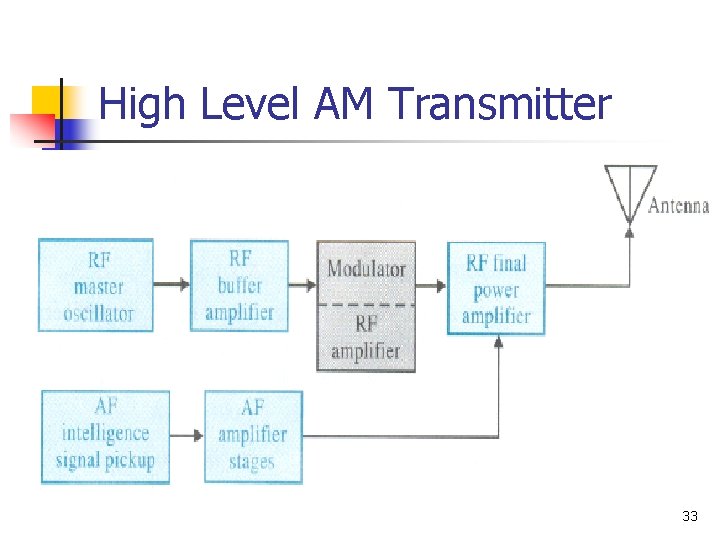
High Level AM Transmitter 33