Modulation Definition One signal carrier varies according to

Modulation

Definition One signal (carrier) varies according to the changes in another signal (modulator) Either amplitude modulation (AM) or frequency modulation (FM).

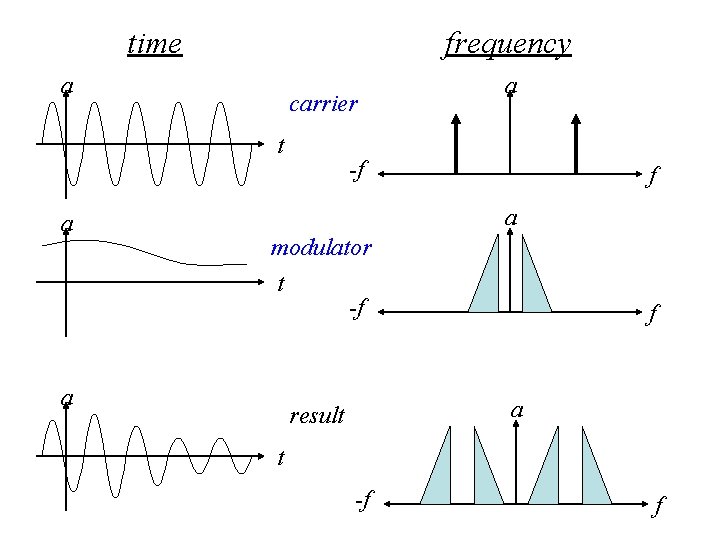
Amplitude Modulation Type #1 balanced/ring/double-sideband suppressed carrier amplitude modulation f 1(t) * f 2(t)

time frequency a carrier t a a -f f a modulator t -f a result t -f f

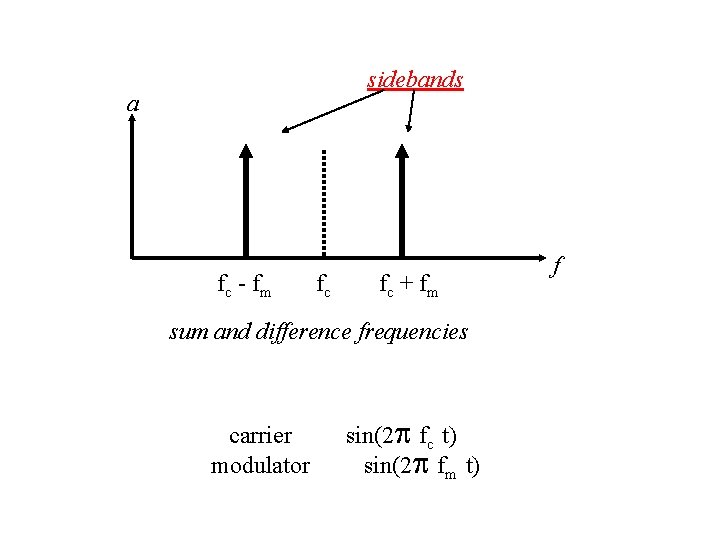
sidebands a fc - f m fc fc + f m sum and difference frequencies carrier modulator sin(2 p fc t) sin(2 p fm t) f

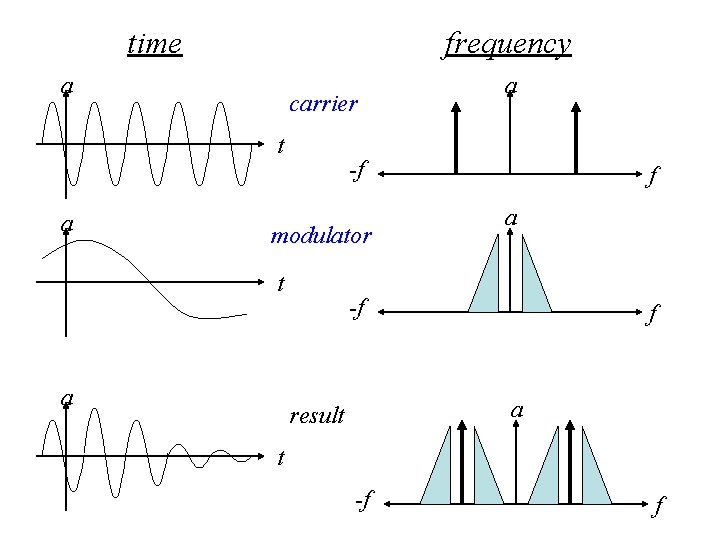
Amplitude Modulation Type #2 double-sideband amplitude modulation 0. 5 * (1. 0 + f 1(t)) * f 2(t) f 1 is offset to range between 0. 0 and 1. 0

time frequency a carrier t a -f modulator t a a f a -f f a result t -f f

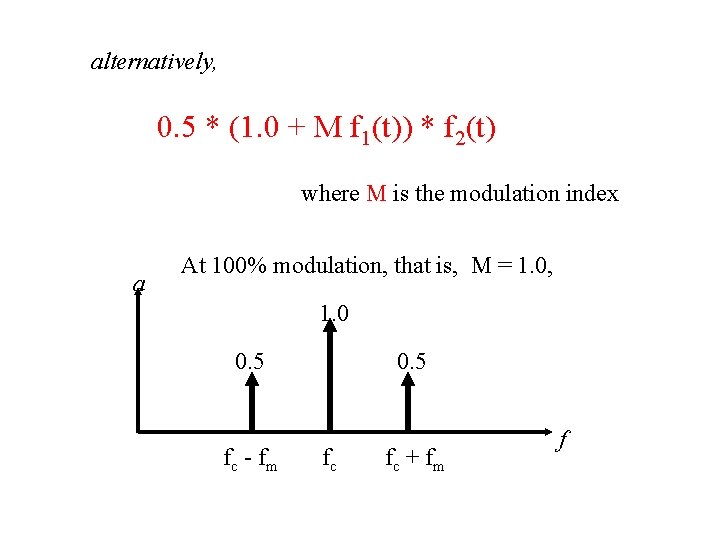
alternatively, 0. 5 * (1. 0 + M f 1(t)) * f 2(t) where M is the modulation index a At 100% modulation, that is, M = 1. 0, 1. 0 0. 5 fc - f m 0. 5 fc fc + f m f

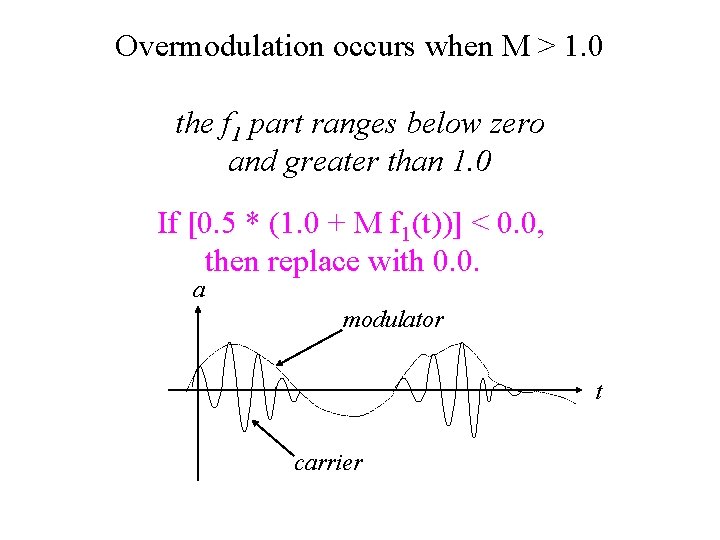
Overmodulation occurs when M > 1. 0 the f 1 part ranges below zero and greater than 1. 0 If [0. 5 * (1. 0 + M f 1(t))] < 0. 0, then replace with 0. 0. a modulator t carrier

Amplitude Modulation Type #3 single-sideband, suppressed carrier amplitude modulation Pretty hard to do digitally!

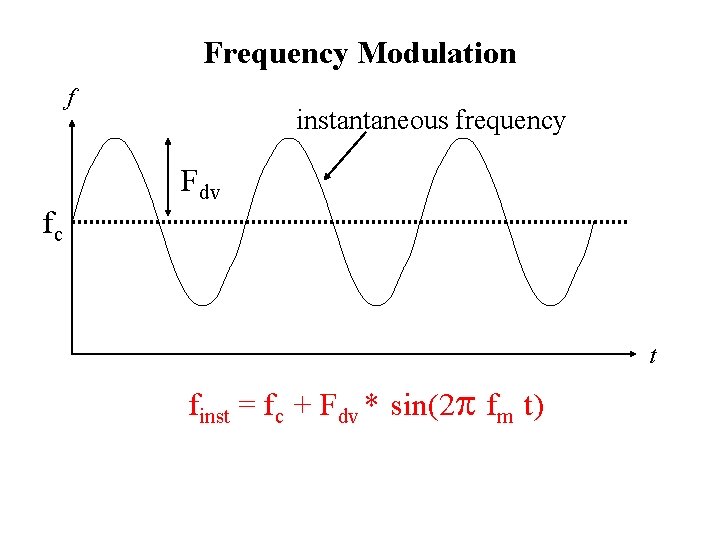
Frequency Modulation finst = fc + Fdv * sin(2 p fm t) amp * sin(2 p finst t) where fc is the carrier frequency, fm is the modulator frequency and finst is the instantaneous frequency

Frequency Modulation f instantaneous frequency Fdv fc t finst = fc + Fdv * sin(2 p fm t)

Frequency Modulation Index M = Fdv / fm Fdv = fm * M finst = fc + fm * M * sin(2 p fm t) amp * sin(2 p finst t)

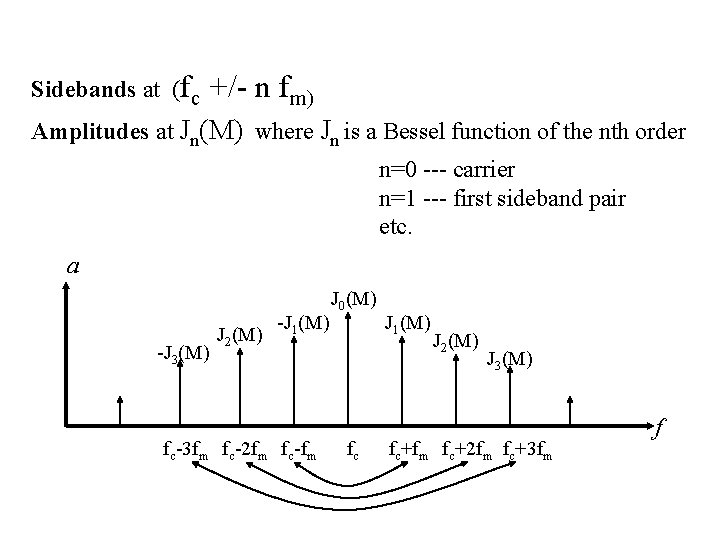
Sidebands at (fc +/- n fm) Amplitudes at Jn(M) where Jn is a Bessel function of the nth order n=0 --- carrier n=1 --- first sideband pair etc. a -J 3(M) J 2(M) -J 1(M) fc-3 fm fc-2 fm fc-fm J 0(M) fc J 1(M) J 2(M) J 3(M) fc+fm fc+2 fm fc+3 fm f

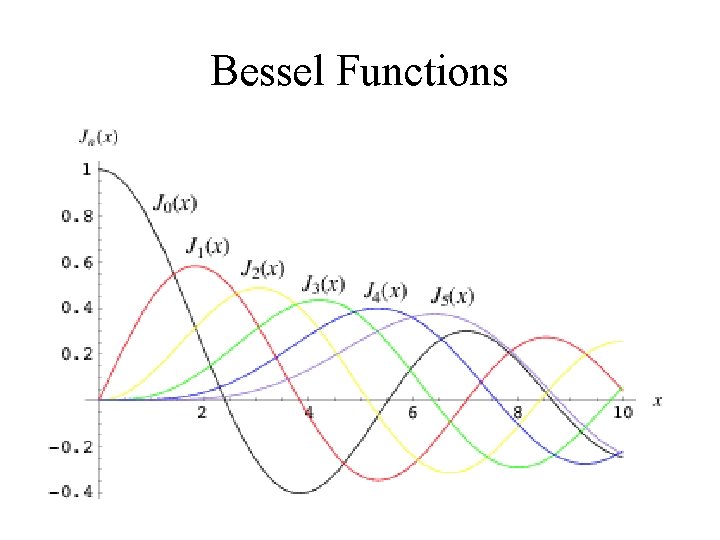
Bessel Functions

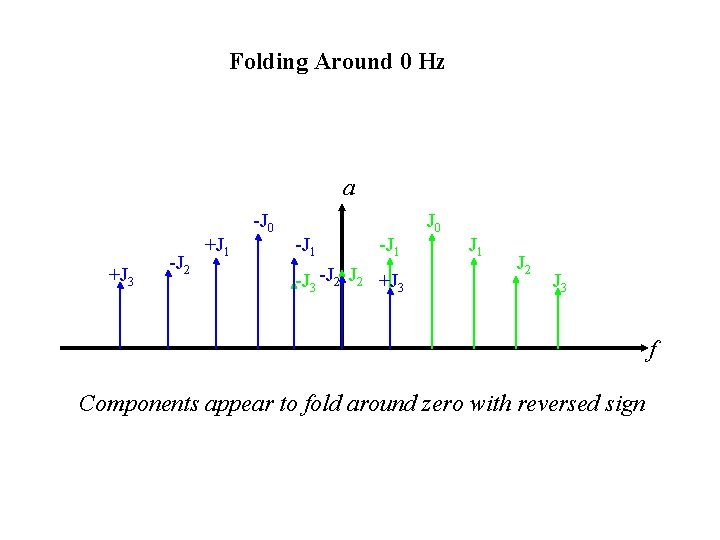
Folding Around 0 Hz a +J 3 -J 2 +J 1 -J 0 -J 1 -J 3 -J 2 +J 3 J 0 J 1 J 2 J 3 f Components appear to fold around zero with reversed sign

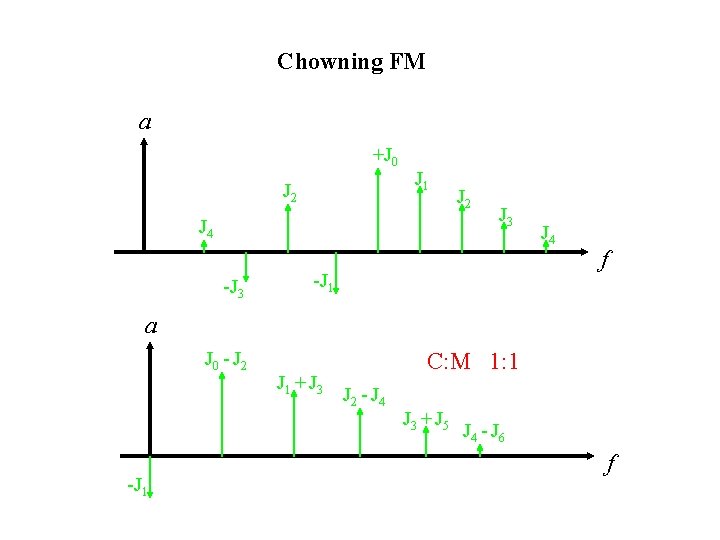
Chowning FM a +J 0 J 2 J 1 J 4 -J 3 J 2 J 3 -J 1 J 4 f a J 0 - J 2 -J 1 + J 3 C: M 1: 1 J 2 - J 4 J 3 + J 5 J 4 - J 6 f

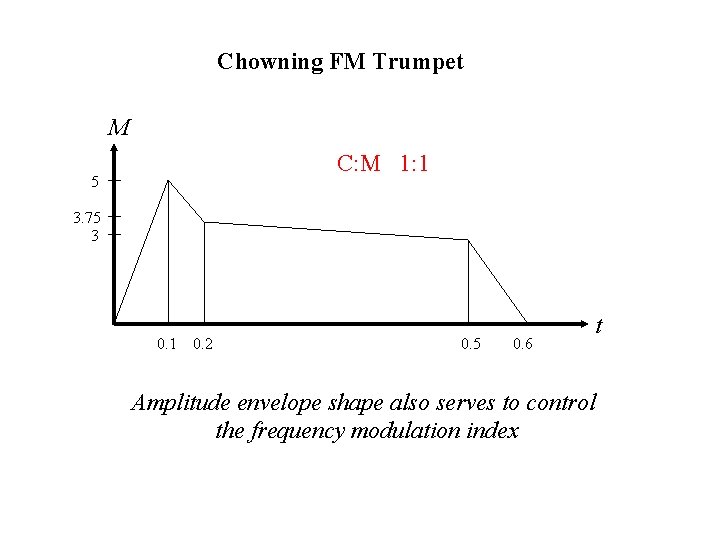
Chowning FM Trumpet M C: M 1: 1 5 3. 75 3 0. 1 0. 2 0. 5 0. 6 t Amplitude envelope shape also serves to control the frequency modulation index

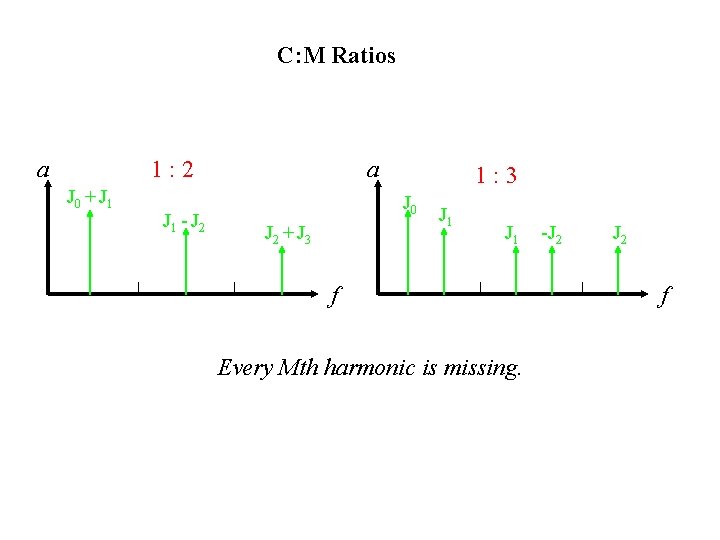
C: M Ratios a 1: 2 J 0 + J 1 - J 2 a 1: 3 J 0 J 2 + J 3 J 1 f Every Mth harmonic is missing. -J 2 f

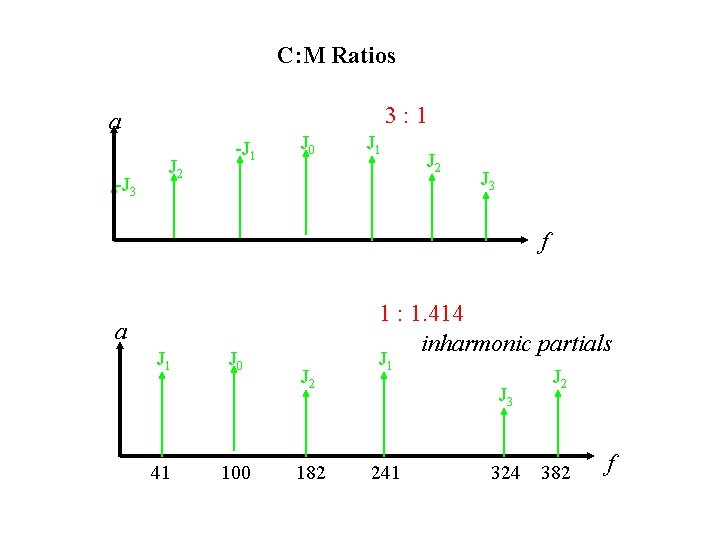
C: M Ratios 3: 1 a -J 3 J 2 -J 1 J 0 J 1 J 2 J 3 f 1 : 1. 414 inharmonic partials a J 1 41 J 0 100 J 2 182 J 1 J 3 241 324 J 2 382 f

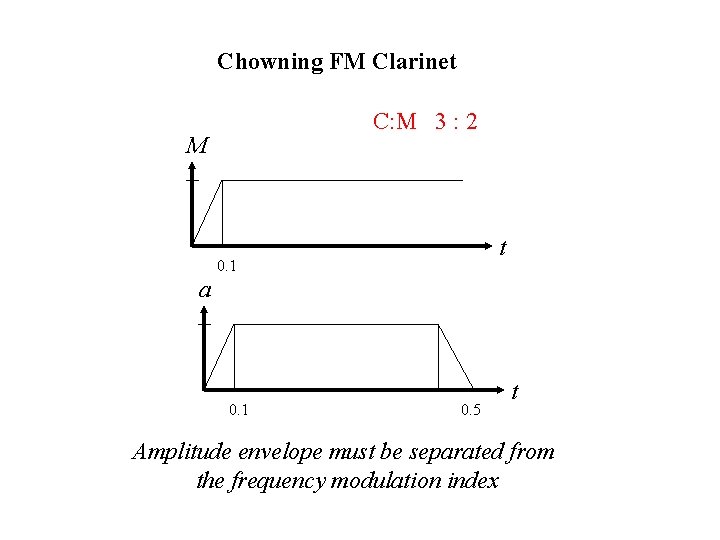
Chowning FM Clarinet C: M 3 : 2 M t 0. 1 a 0. 1 0. 5 t Amplitude envelope must be separated from the frequency modulation index

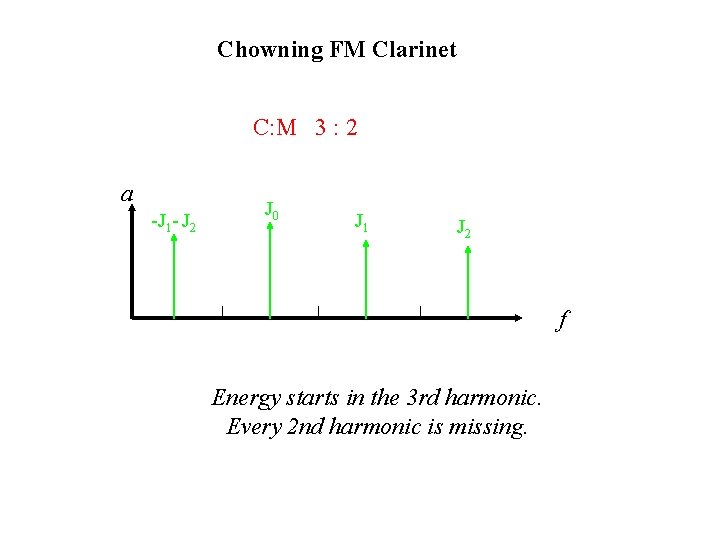
Chowning FM Clarinet C: M 3 : 2 a -J 1 - J 2 J 0 J 1 J 2 f Energy starts in the 3 rd harmonic. Every 2 nd harmonic is missing.

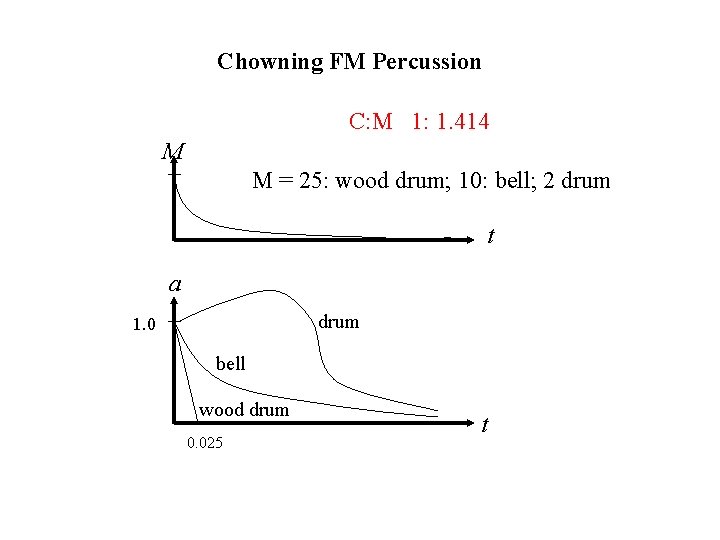
Chowning FM Percussion C: M 1: 1. 414 M M = 25: wood drum; 10: bell; 2 drum t a drum 1. 0 bell wood drum 0. 025 t

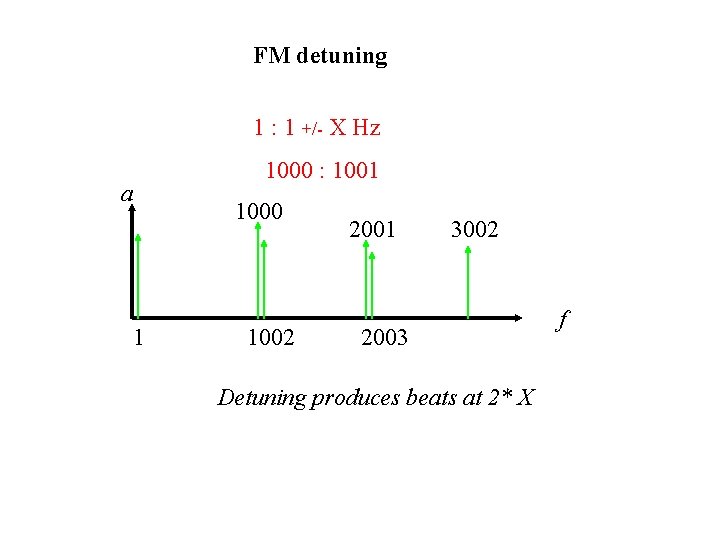
FM detuning 1 : 1 +/- X Hz 1000 : 1001 a 1000 1 1002 2001 3002 2003 Detuning produces beats at 2* X f

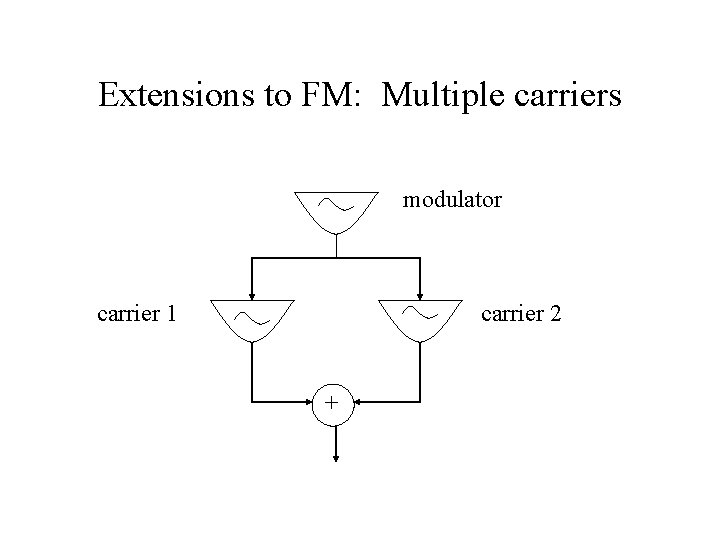
Extensions to FM: Multiple carriers modulator carrier 1 carrier 2 +

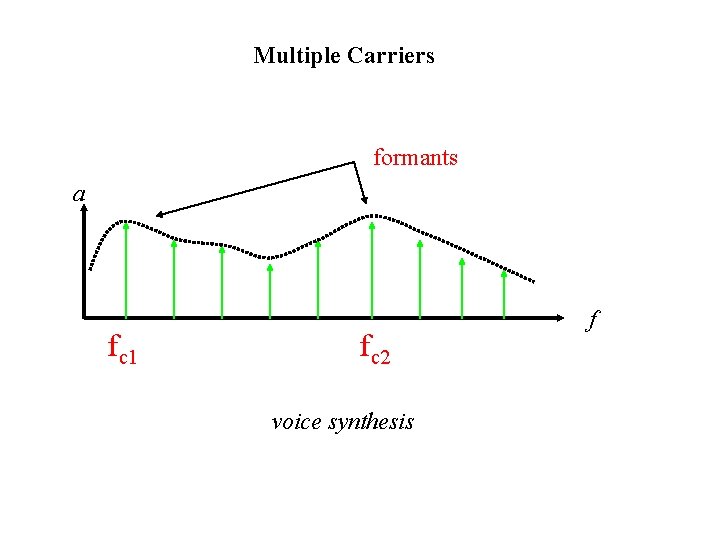
Multiple Carriers formants a fc 1 fc 2 voice synthesis f

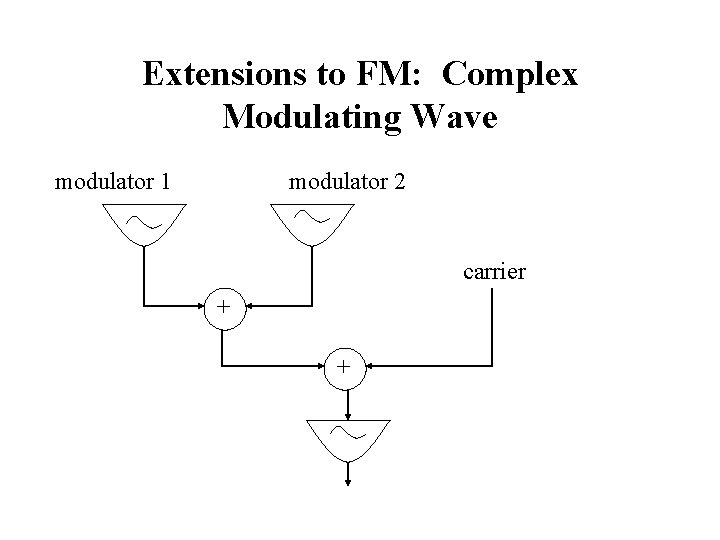
Extensions to FM: Complex Modulating Wave modulator 1 modulator 2 carrier + +

Multiple Modulator Sidebands Multiple Modulator FM produces sidebands at fc +/- i fm 1 +/- k fm 2 like one FM pair is modulated by the other (fc +/- i fm 1 ) +/- k fm 2

Multiple Modulator Sidebands Example C: M 1 : M 2 1 : 1: 4 M 1 = 1, M 2 = 0. 2 All cross combinations are formed 1: 1 1: 4 J 0. 77. 98 J 1. 44. 10 J 2. 12. 005 J 3. 02 Spreads energy out and limits the influence of dynamic M

Example: String Synthesis • • 1: 1: 3: 4 Each M dependent on frequency 5 -6 Hz Vibrato 10 -20 Hz random fluctuations Attack noise: 20% to 0% in. 2 sec M +1 for. 2 sec Detuning 1. 5 to 4 Hz