Modular analysis of a circuit description language by

Modular analysis of a circuit description language by Abstract Interpretation Application to the automatic extraction of circuit shapes Charles Hymans

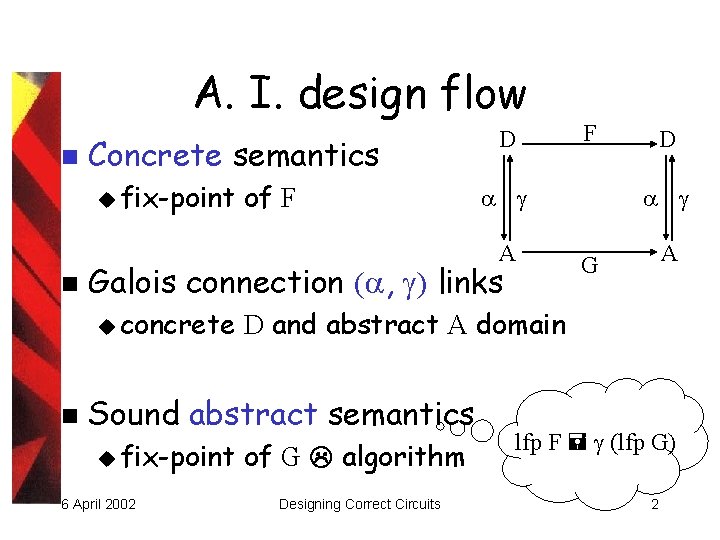
A. I. design flow n Concrete semantics u fix-point of F D A n Galois connection ( , ) links u concrete n 6 April 2002 D A G D and abstract A domain Sound abstract semantics u fix-point F of G algorithm Designing Correct Circuits lfp F (lfp G) 2

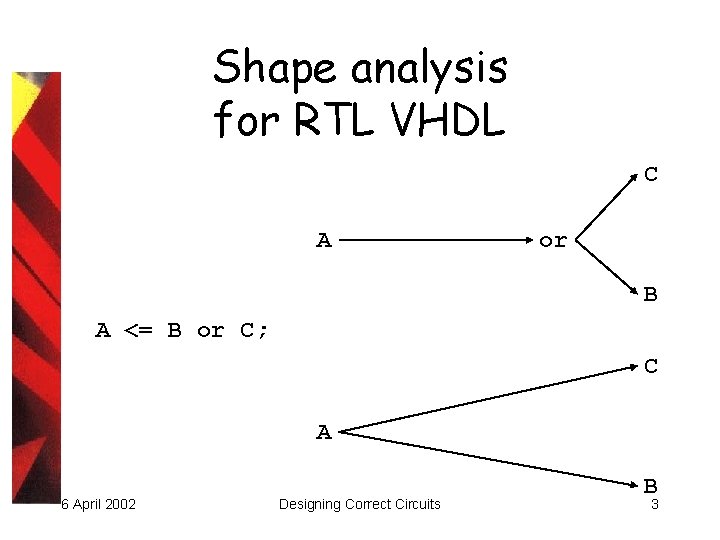
Shape analysis for RTL VHDL C A or B A <= B or C; C A 6 April 2002 Designing Correct Circuits B 3

Generic modules? entity example generic(n : integer) port(A : bit_vector(1 to n), B : bit_vector(1 to 2*n)) for I in 1 to n A[I] <= not B[I + 1]; end; 6 April 2002 Designing Correct Circuits No a-priori bound on n! 4

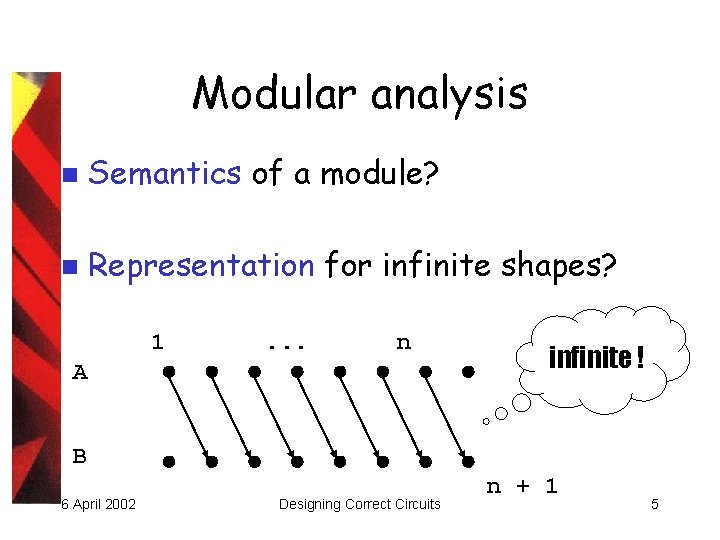
Modular analysis n Semantics of a module? n Representation for infinite shapes? 1 . . . n A infinite ! B 6 April 2002 Designing Correct Circuits n + 1 5

Operational semantics n Execution builds a circuit n State : (l, E, G, S) n VHDL command basic operators n 7 basic operators modify (E, G) u assert, 6 April 2002 create_int, connect. . . Designing Correct Circuits 6

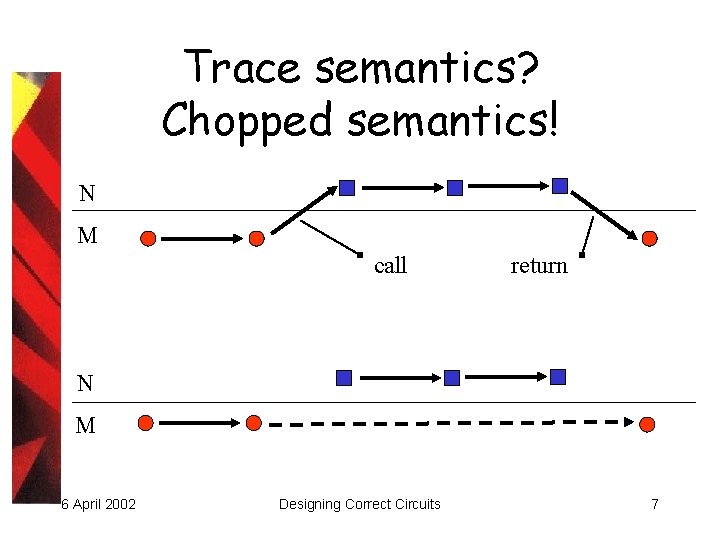
Trace semantics? Chopped semantics! N M call return N M 6 April 2002 Designing Correct Circuits 7

Fix-point for chopped semantics n F(X)(g) = entry(g) {s 0 … sn+1 | s 0 … sn X(g), sn sn+1 } {s 0 … sn+1 | s 0 … sn X(g), sn call(f), sn t 0, t 0 … tm X(f), tm return, tm sn+1 } 6 April 2002 Designing Correct Circuits 8

Abstract domain At each program point l n Possible values of integer variables u numerical n domain Shapes built since module entry u decorated 6 April 2002 connection graph Designing Correct Circuits 9

Numerical domains Symbolic representation for numerical functions Intervals u affine subspaces u octagons u polyhedra u 6 April 2002 X [a. X, b. X] Y [a. Y, b. Y] a. X + b. Y = c X Y c a. X + b. Y c Designing Correct Circuits 10

Decorated connection graph infinite ! for I in 1 to n A[I] <= not B[I + 1]; end; 1 . . . n A A l+1=r B n+1 6 April 2002 finite ! Designing Correct Circuits B 11

Abstract operators n n Operational semantics expressed thanks to 7 basic operators Design only u abstract operators u abstract module plug-in n sound operators sound analysis 6 April 2002 Designing Correct Circuits 12

Example: wire connection n A[2*I + 1] <= not B[J]; left expression: l = 2*I + 1 n environment: I = J n right expression: r = J n n resulting constraint: l = 2 * r + 1 6 April 2002 Designing Correct Circuits 13

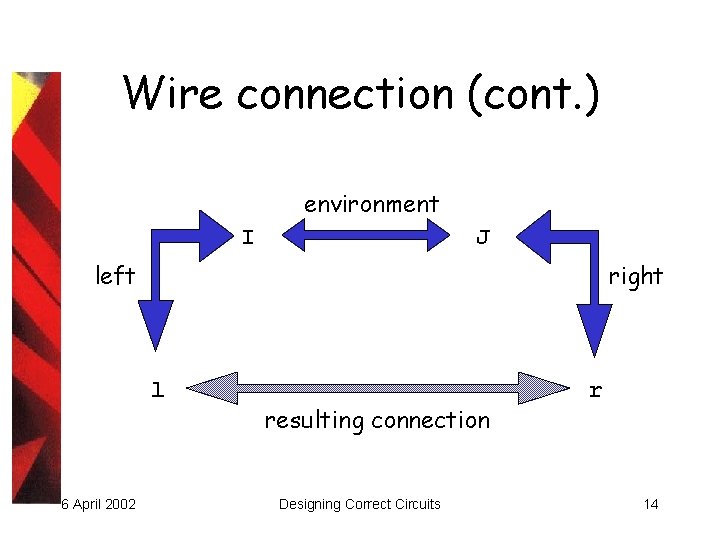
Wire connection (cont. ) environment I J left right l 6 April 2002 resulting connection Designing Correct Circuits r 14

Conclusion Modular analysis n Decorated connection graph n Quickly applicable to other languages n Data-dependency: all VHDL n Timed dependencies: n u “B 6 April 2002 depends on A with a delay of 3 cycles” Designing Correct Circuits 15

Thank you for your attention!