Modul 2 Physical Chemistry 2 Persamaan Clapeyron dan

Modul 2 Physical Chemistry 2 Persamaan Clapeyron dan Persamaan Clausius. Clapeyron Dr. M. Masykuri, M. Si. Chemistry Education Study Program Teacher Training and Education Faculty Sebelas Maret Universitfy (UNS) Website: http: //mmasykuri. wordpress. com, email: mmasykuri@yahoo. com Teacher Training and Education Faculty 4/26/2020 Sebelas Maret University 1 M. Masykuri_Physical Chemistry 2 Feb 2020 Solo, Peb 2020

Outline 1. 2. 3. 4. Persamaan Clapeyron Persamaan Clausius-Clapeyron Aturan Trouton Mengkonstruksi Diagram Fasa Teacher Training and Education Faculty Sebelas Maret University M. Masykuri_Physical Chemistry 2 Feb 2020

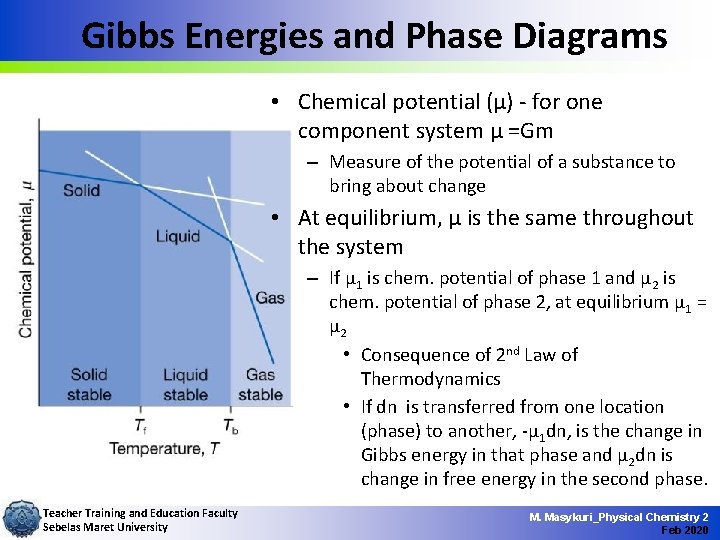
Gibbs Energies and Phase Diagrams • Chemical potential (µ) - for one component system µ =Gm – Measure of the potential of a substance to bring about change • At equilibrium, µ is the same throughout the system – If µ 1 is chem. potential of phase 1 and µ 2 is chem. potential of phase 2, at equilibrium µ 1 = µ 2 • Consequence of 2 nd Law of Thermodynamics • If dn is transferred from one location (phase) to another, -µ 1 dn, is the change in Gibbs energy in that phase and µ 2 dn is change in free energy in the second phase. Teacher Training and Education Faculty Sebelas Maret University M. Masykuri_Physical Chemistry 2 Feb 2020

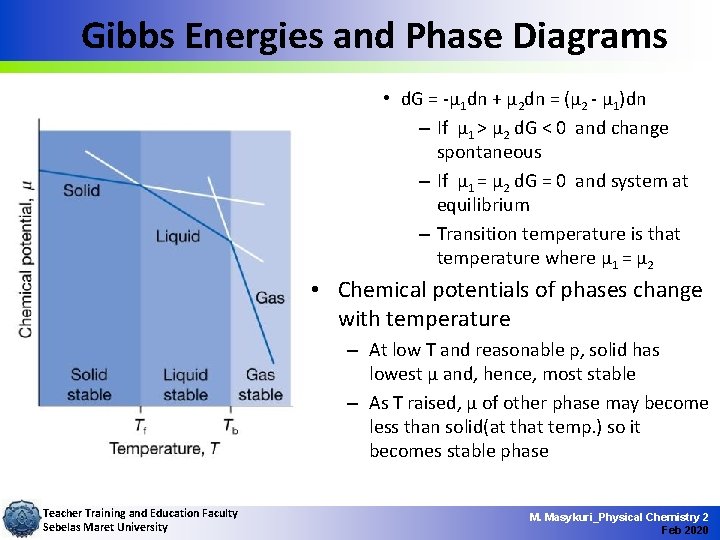
Gibbs Energies and Phase Diagrams • d. G = -µ 1 dn + µ 2 dn = (µ 2 - µ 1)dn – If µ 1 > µ 2 d. G < 0 and change spontaneous – If µ 1 = µ 2 d. G = 0 and system at equilibrium – Transition temperature is that temperature where µ 1 = µ 2 • Chemical potentials of phases change with temperature – At low T and reasonable p, solid has lowest µ and, hence, most stable – As T raised, µ of other phase may become less than solid(at that temp. ) so it becomes stable phase Teacher Training and Education Faculty Sebelas Maret University M. Masykuri_Physical Chemistry 2 Feb 2020

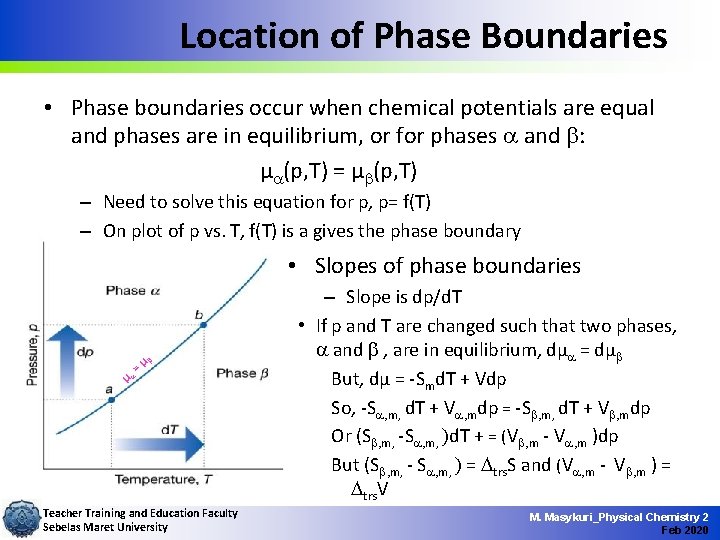
Location of Phase Boundaries • Phase boundaries occur when chemical potentials are equal and phases are in equilibrium, or for phases a and b: µa(p, T) = µb(p, T) – Need to solve this equation for p, p= f(T) – On plot of p vs. T, f(T) is a gives the phase boundary • Slopes of phase boundaries =µ b µa Teacher Training and Education Faculty Sebelas Maret University – Slope is dp/d. T • If p and T are changed such that two phases, a and b , are in equilibrium, dµa = dµb But, dµ = -Smd. T + Vdp So, -Sa, m, d. T + Va, mdp = -Sb, m, d. T + Vb, mdp Or (Sb, m, -Sa, m, )d. T + = (Vb, m - Va, m )dp But (Sb, m, - Sa, m, ) = trs. S and (Va, m - Vb, m ) = trs. V M. Masykuri_Physical Chemistry 2 Feb 2020

Location of Phase Boundaries • This rearranges to: dp/d. T = Dtrs. S / Dtrs. V where and are the entropy and volume of transition – This is called the Clapeyron Equation =µ b µa Teacher Training and Education Faculty Sebelas Maret University • Exact expression for the phase boundary at equilibrium • Can be used to predict appearance of phase diagrams and form of boundaries M. Masykuri_Physical Chemistry 2 Feb 2020

Solid-Liquid Boundary • For solid-liquid boundary, Clapeyron Equation becomes dp/d. T = Dfus. S / Dfus. V where fus. V is the change in molar volume on melting • fus. S is always positive (except for 3 He) and fus. V is usually small so dp/d. T is large (steep slope) and positive • Formula for phase boundary comes from integrating Clapeyron equation Teacher Training and Education Faculty Sebelas Maret University M. Masykuri_Physical Chemistry 2 Feb 2020

Solid-Liquid Boundary Teacher Training and Education Faculty Sebelas Maret University M. Masykuri_Physical Chemistry 2 Feb 2020

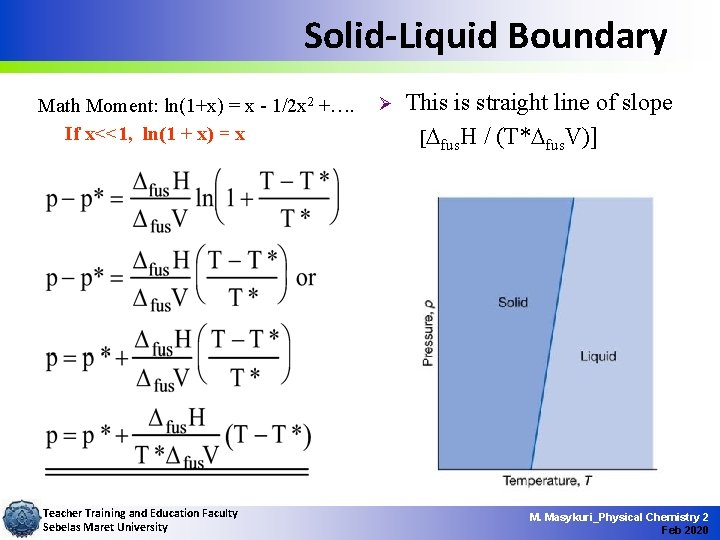
Solid-Liquid Boundary Math Moment: ln(1+x) = x - 1/2 x 2 +…. If x<<1, ln(1 + x) = x Teacher Training and Education Faculty Sebelas Maret University Ø This is straight line of slope [ fus. H / (T* fus. V)] M. Masykuri_Physical Chemistry 2 Feb 2020

Liquid-Vapor Boundary • Again, Clapeyron equation can be used » » » vap. V is large and positive so dp/d. T is positive, but smaller than for solid-liquid transition vap. H/T is Trouton’s constant Because Vm(gas) >> Vm(liquid), vap. V ≈ Vm(gas) Ù Ø For ideal gas, Vm(gas) = RT/p so vap. V ≈ RT/p Clapeyron equation becomes Teacher Training and Education Faculty Sebelas Maret University M. Masykuri_Physical Chemistry 2 Feb 2020

Liquid-Vapor Boundary Ø Integrating Clausius-Clapeyron equation gives variation of vapor pressure with temperature Assumes vap. H is independent of T and p* is vapor pressure at T* and p the vapor pressure at T » » This is a curve, not a line Does not extend beyond Tc Teacher Training and Education Faculty Sebelas Maret University M. Masykuri_Physical Chemistry 2 Feb 2020

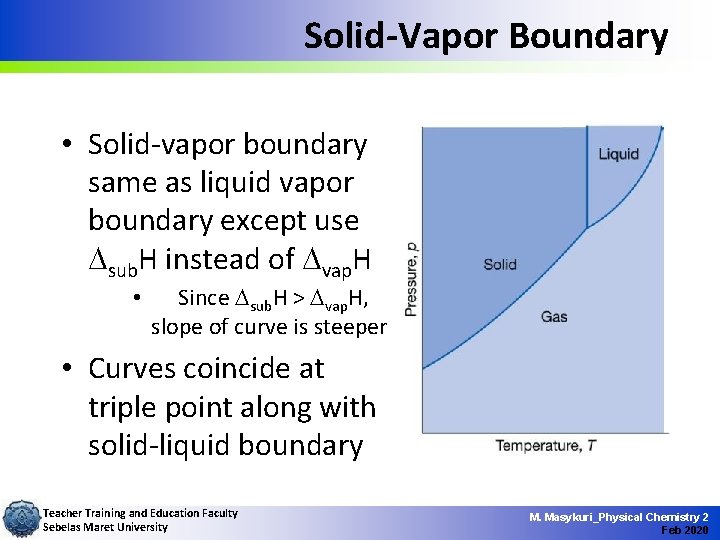
Solid-Vapor Boundary • Solid-vapor boundary same as liquid vapor boundary except use sub. H instead of vap. H • Since sub. H > vap. H, slope of curve is steeper • Curves coincide at triple point along with solid-liquid boundary Teacher Training and Education Faculty Sebelas Maret University M. Masykuri_Physical Chemistry 2 Feb 2020

Solid-Vapor Boundary • Solid-vapor boundary same as liquid vapor boundary except use sub. H instead of vap. H • Since sub. H > vap. H, slope of curve is steeper • Curves coincide at triple point along with solid-liquid boundary Teacher Training and Education Faculty Sebelas Maret University M. Masykuri_Physical Chemistry 2 Feb 2020

LATIHAN The normal freezing point for benzene (C 6 H 6, M = 78. 12 g/mol) is T fus = 5. 50 C. The density of liquid and solid benzene at the normal freezing point are (s) = 0. 891 g/cm 3, (� ) = 0. 879 g/cm 3, and the enthalpy of fusion for benzene is H fus = 10. 59 k. J/mol. a) Based on the above data, estimate the freezing point of benzene when p = 1000. atm (be careful about using consistent units). b) The vapor pressure of liquid benzene above the triple point temperature (in units of torr) is given by the expression log 10 p = 7. 960 – 1780. K T Using equn 4. 1, find the pressure of benzene at the triple point, and the normal boiling point for benzene. Teacher Training and Education Faculty Sebelas Maret University M. Masykuri_Physical Chemistry 2 Feb 2020

Teacher Training and Education Faculty Sebelas Maret University M. Masykuri_Physical Chemistry 2 Feb 2020