Modern Solid State NMR Techniques for the Study

Modern Solid State NMR Techniques for the Study of Glasses Hellmut Eckert Institut of Physics, Sao Carlos University of Sao Paulo, Brazil

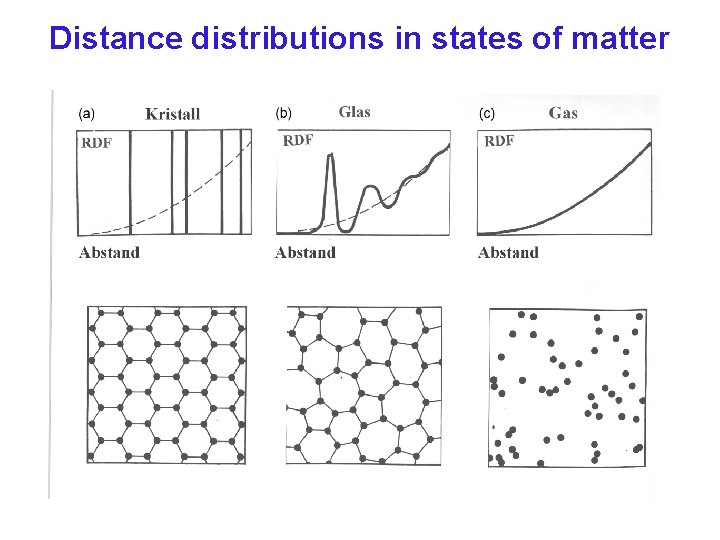
Distance distributions in states of matter

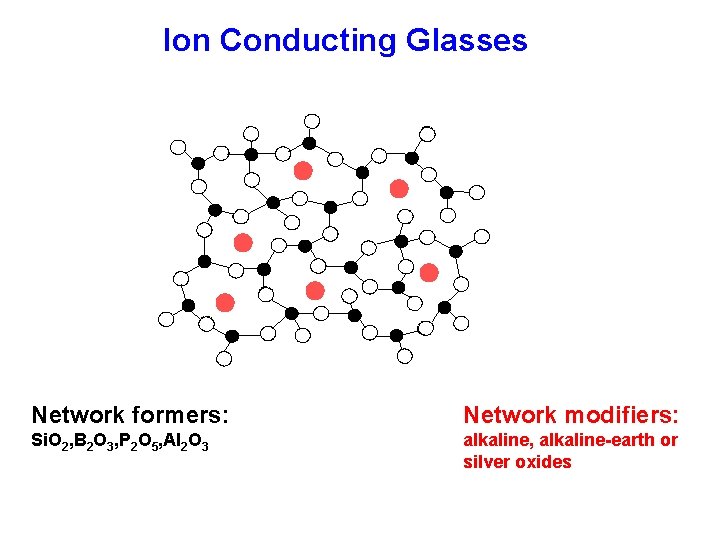
Ion Conducting Glasses Network formers: Network modifiers: Si. O 2, B 2 O 3, P 2 O 5, Al 2 O 3 alkaline, alkaline-earth or silver oxides

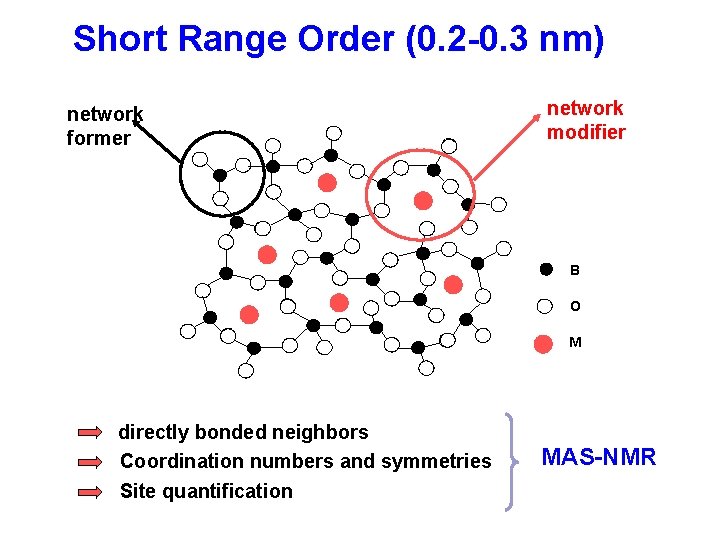
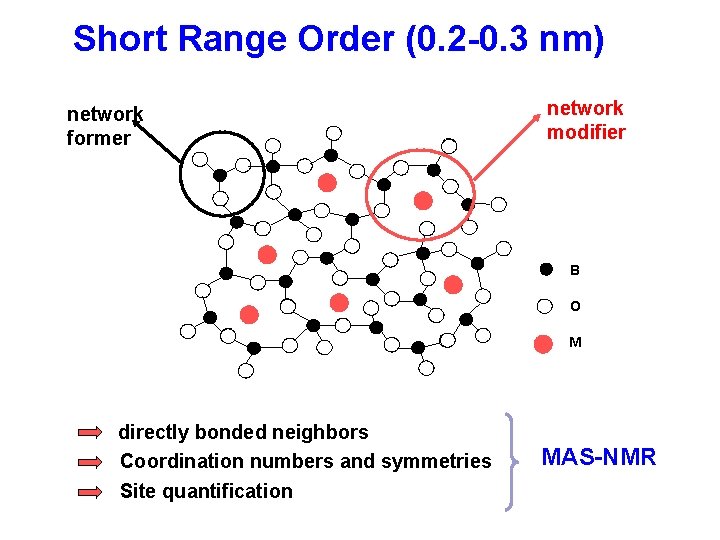
Short Range Order (0. 2 -0. 3 nm) network former network modifier B O M directly bonded neighbors Coordination numbers and symmetries Site quantification MAS-NMR

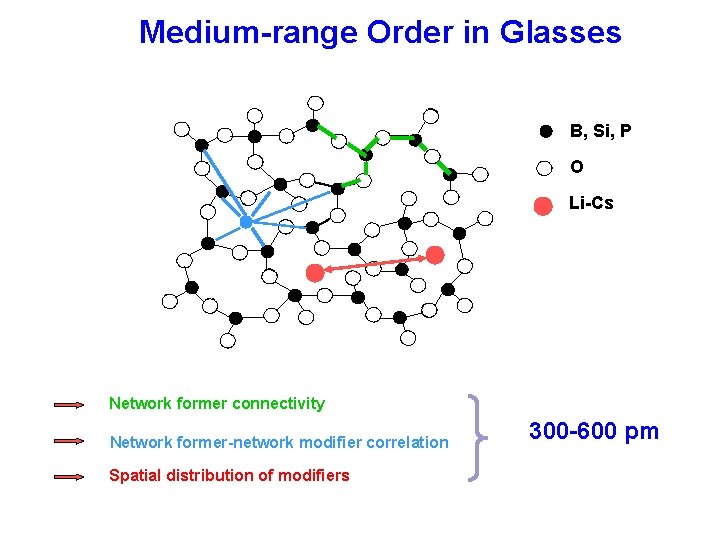
Medium-range Order in Glasses B, Si, P O Li-Cs Network former connectivity Network former-network modifier correlation Spatial distribution of modifiers 300 -600 pm

Nano- and Microstructure • Chemical Segregation, • Phase Separation, • Nucleation/growth > 1 nm

NMR = Nuclear Magnetic Resonance N: Property of the Atomic Nuclei in Matter M: Magnetic Property, arising from Spin Angular Momentum R: Interaction with electromagnetic waves spectroscopy

Solid State NMR applications to inorganic materials AK H. Eckert eckert@ifsc. usp. br eckerth@uni-muenster. de Methods Development Glass Science Li Ion battery Components Hybrid Materials Biomaterials FK-NMR, ESR Raman, Preparation history, Sol-Gel electrodes Glasses, polymers Zeolites Bioceramics Inclusion Comp. Implants Nanocomposites Biopolymers Support 1. 2. 3. 4. 5. Glass/Ceramics Industry: Corning, Schott, Ivoclar, Nippon Glass Fond der Chemischen Industrie State of NRW (Instrumentation und GSC) DFG/ SFB 858 / IRTG Research Networks FAPESP, CNPq – 1 A

Outline Solid State NMR – General Aspects Anisotropic Interactions: magnetic shielding dipole-dipole coupling nuclear electric quadrupole coupling Manipulation of Interactions magic angle spinning NMR dipolar spectroscopy –homonuclear dipolar spectroscopy –heteronuclear Some Applications to Glasses

Literature Highlight articles D. Laws, H. M. Bitter, A. Jerschow, Angew. Chem. Int. Ed. 41 (2002), 3096. M. J. Duer, Ann. Rep. NMR Spectrosc. 43 (2000), 1. Fundamental Principles (Theory) A. Abragam, The Principles of Nuclear Magnetism, Clarendon Press Oxford (1961). C. P. Slichter, Principles of Magnetic Resonance, Springer Verlag Heidelberg 1978. B. C. Gerstein, C. R. Dybowski, Transient Techniques in NMR of Solids, Academic Press Inc (1985). M. Mehring, Principles of High Resolution NMR in Solids, Springer Verlag Heidelberg (1983) R. R. Ernst, G. Bodenhausen, A. Wokaun, Principles of Nuclear Magnetic Resonance in One and Two Dimensions, Clarendon Press, Oxford (1987) NMR Applications to Materials Sciences J. Klinowski, Ed. New Techniques in Solid State NMR, Topics in Current Chemistry, 246, Springer-Verlag Heidelberg 2005. K. Schmidt-Rohr, H. W. Spiess, Multidimensional Solid-State NMR and Polymers, Academic Press, London (1996). M. J. Duer, Introduction into Solid State NMR Spectroscopy, Blackwell Publ. 2004

Nuclear Magnetism Nuclear magnetic moment: I, the angular momentum, is subject to quantization laws, concerning both magnitude and orientation I: m: spin quantum number orientational quantum number with m=-I, -I+1, …I-1, I

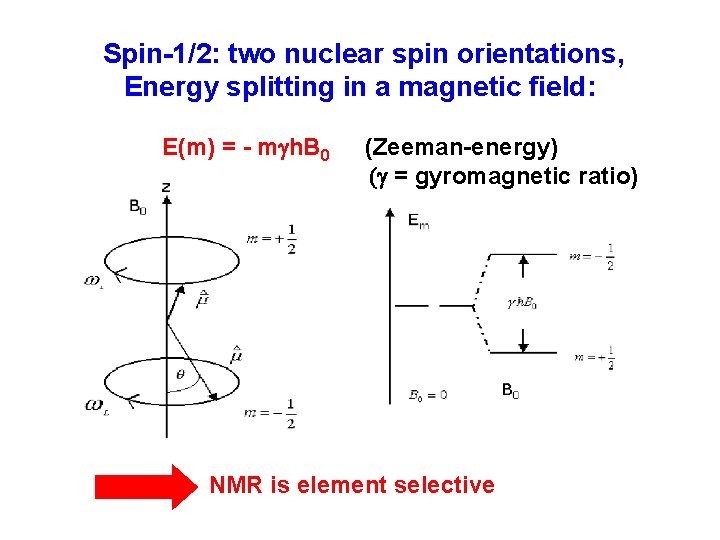
Spin-1/2: two nuclear spin orientations, Energy splitting in a magnetic field: E(m) = - mgh. B 0 (Zeeman-energy) (g = gyromagnetic ratio) NMR is element selective

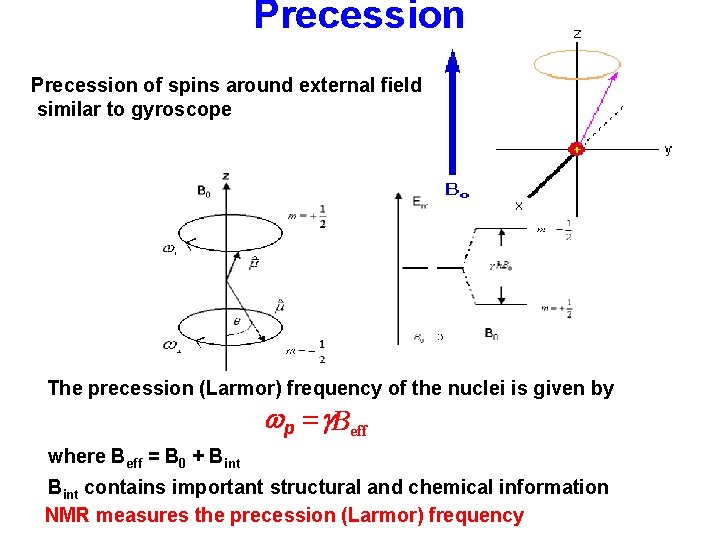
Precession of spins around external field similar to gyroscope The precession (Larmor) frequency of the nuclei is given by wp = g. Beff where Beff = B 0 + Bint contains important structural and chemical information NMR measures the precession (Larmor) frequency

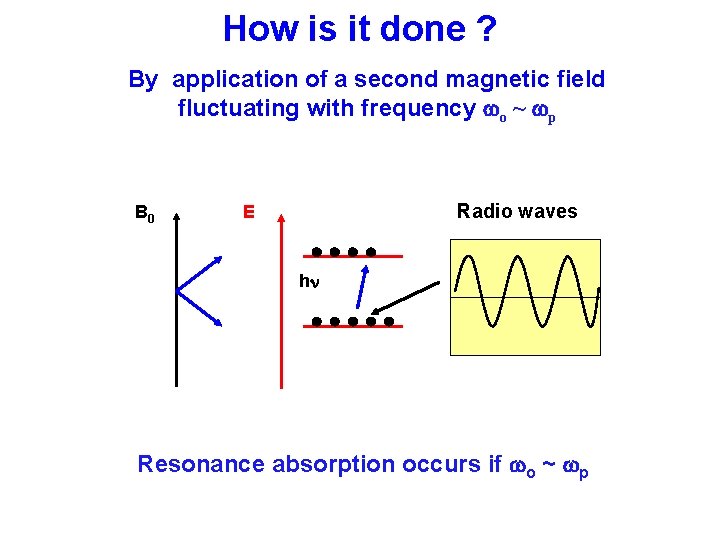
How is it done ? By application of a second magnetic field fluctuating with frequency wo ~ wp B 0 Radio waves E hn Resonance absorption occurs if wo ~ wp

Macroscopic Sample In a sample spins are distributed among energy levels ( Boltzmann-distribution)l Macroscopic magnetization along B 0 No net magnetization in x- or y-direction Curie Law NMR is quantitative

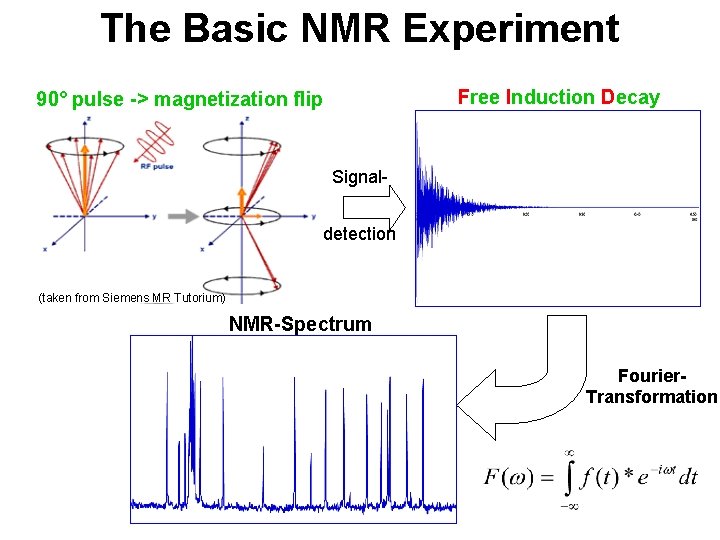
The Basic NMR Experiment Free Induction Decay 90° pulse -> magnetization flip Signaldetection (taken from Siemens MR Tutorium) NMR-Spectrum Fourier. Transformation

Equipment Magnet Probe Sample in Rotor Console /Computer

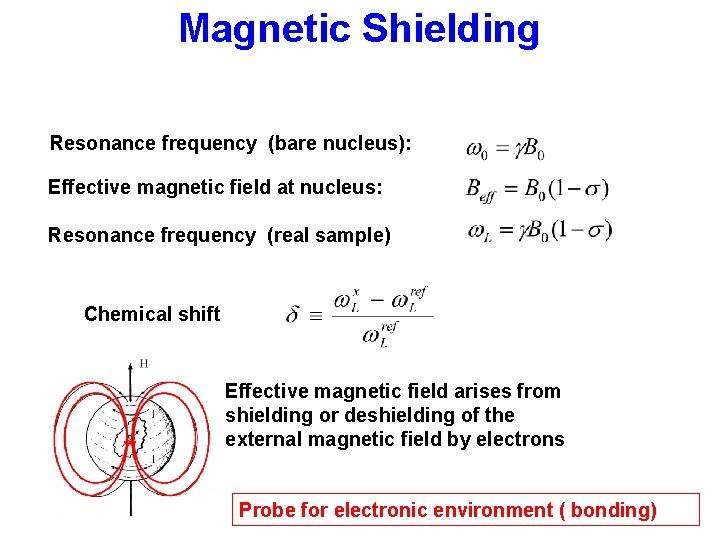
Magnetic Shielding Resonance frequency (bare nucleus): Effective magnetic field at nucleus: Resonance frequency (real sample) Chemical shift Effective magnetic field arises from shielding or deshielding of the external magnetic field by electrons Probe for electronic environment ( bonding)

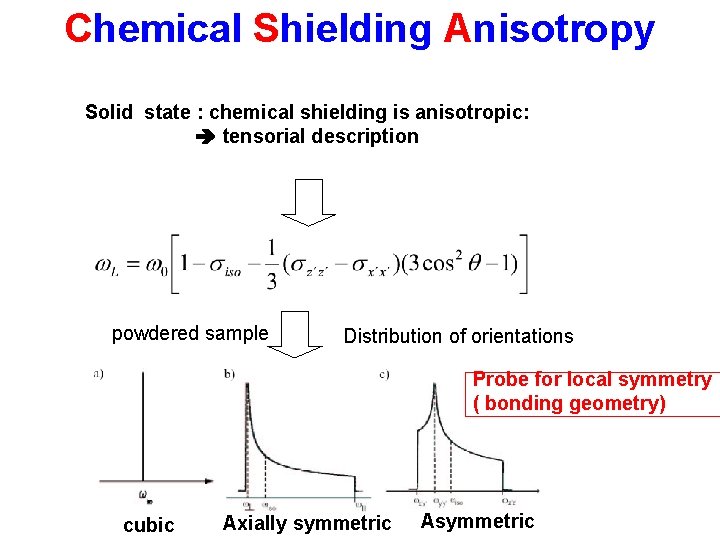
Chemical Shielding Anisotropy Solid state : chemical shielding is anisotropic: tensorial description powdered sample Distribution of orientations Probe for local symmetry ( bonding geometry) cubic Axially symmetric Asymmetric

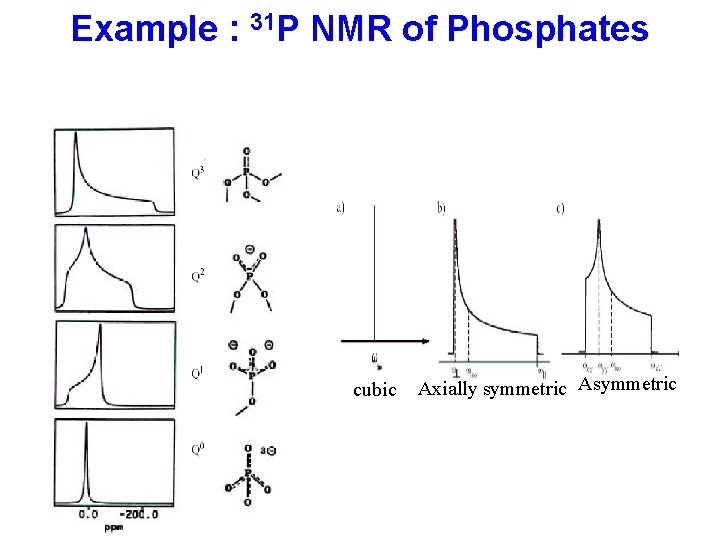
Example : 31 P NMR of Phosphates cubic Axially symmetric Asymmetric

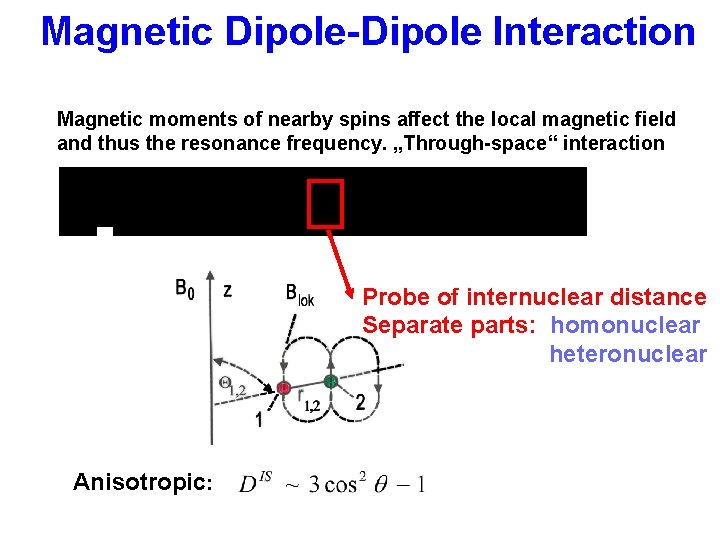
Magnetic Dipole-Dipole Interaction Magnetic moments of nearby spins affect the local magnetic field and thus the resonance frequency. „Through-space“ interaction Probe of internuclear distance Separate parts: homonuclear heteronuclear Anisotropic:

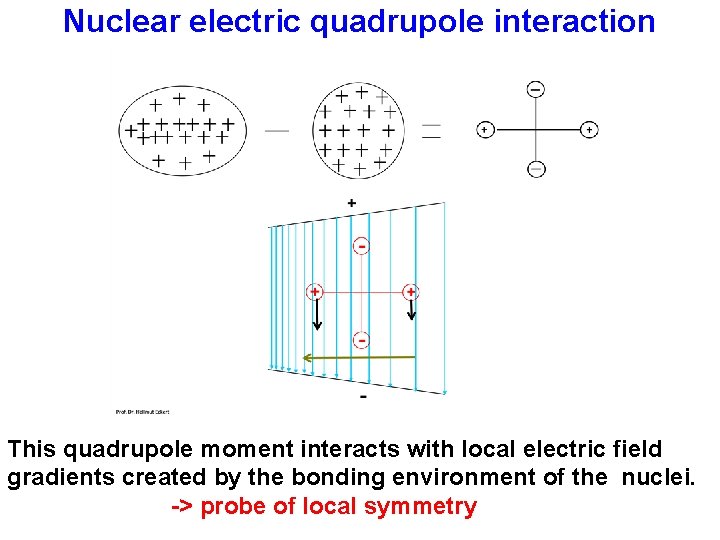
Nuclear electric quadrupole interaction This quadrupole moment interacts with local electric field gradients created by the bonding environment of the nuclei. -> probe of local symmetry

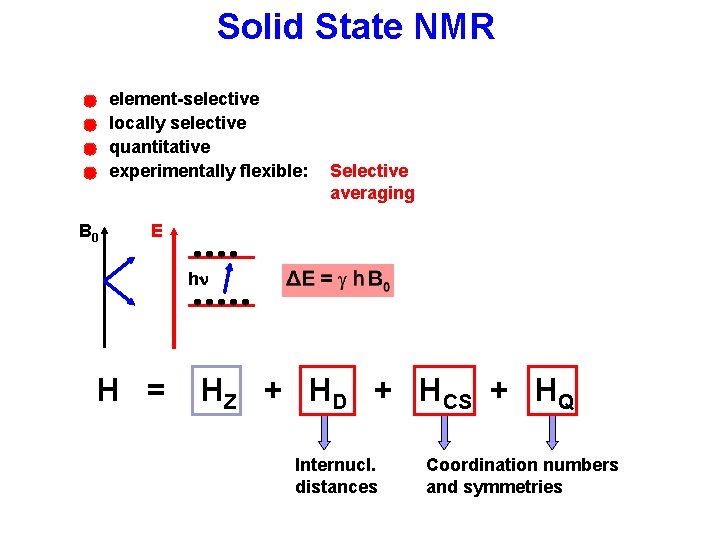
Solid State NMR element-selective locally selective quantitative experimentally flexible: B 0 Selective averaging E hn H = HZ + HD + HCS + HQ Internucl. distances Coordination numbers and symmetries

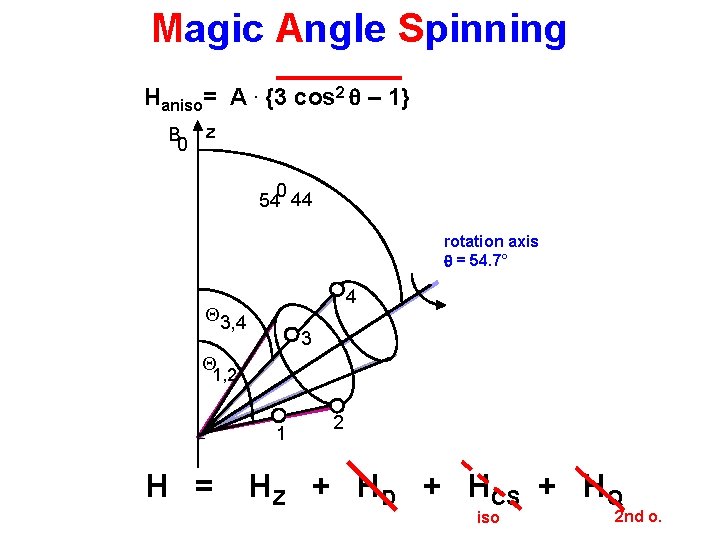
Magic Angle Spinning Haniso= A. {3 cos 2 q – 1} B 0 z 0 54 44 rotation axis q = 54. 7° 4 Q 3, 4 3 Q 1, 2 1 H = 2 HZ + HD + HCS + HQ iso 2 nd o.

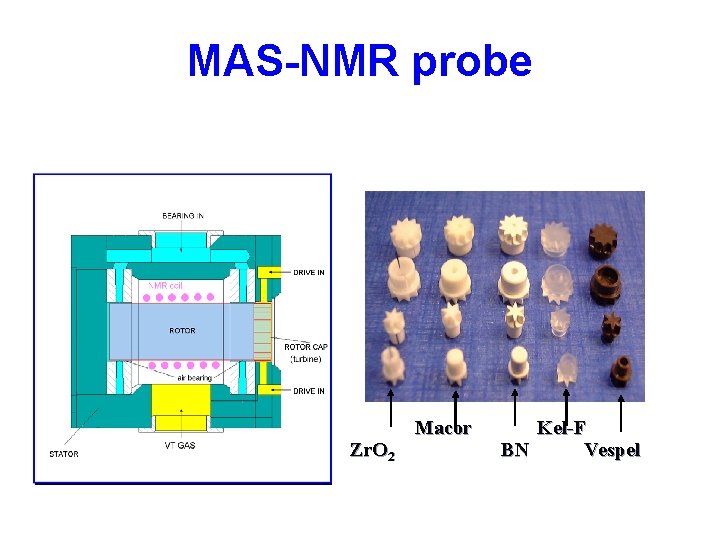
MAS-NMR probe Zr. O 2 Macor Kel-F BN Vespel

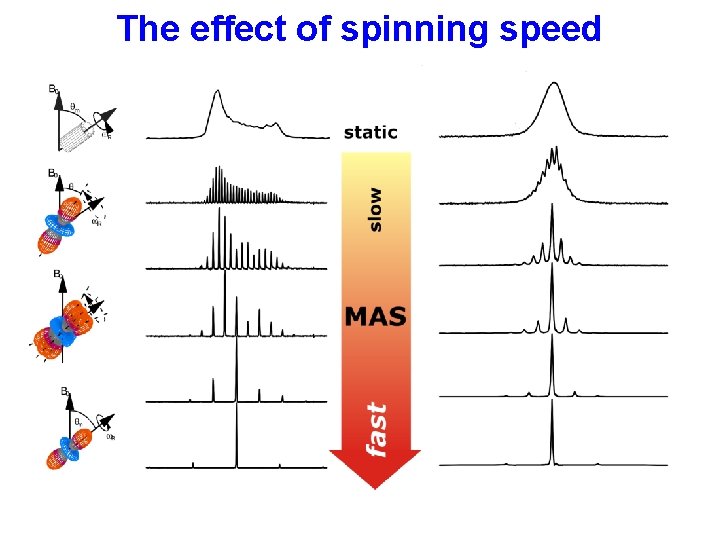
The effect of spinning speed

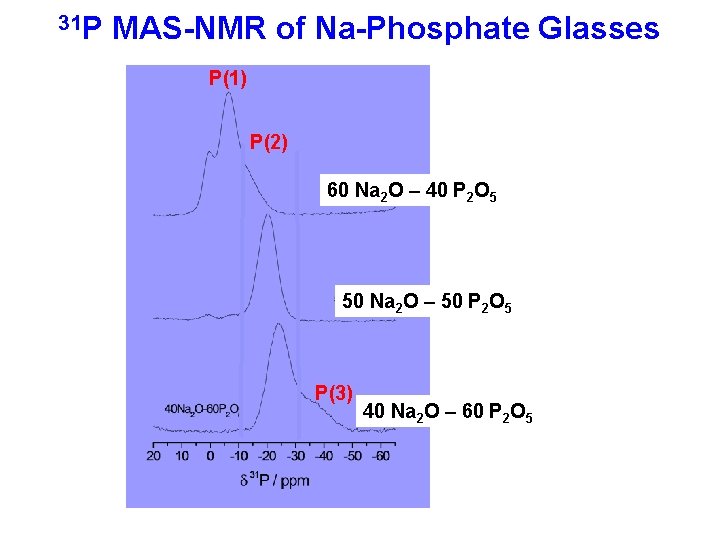
31 P MAS-NMR of Na-Phosphate Glasses P(1) P(2) 60 Na 2 O – 40 P 2 O 5 50 Na 2 O – 50 P 2 O 5 P(3) 40 Na 2 O – 60 P 2 O 5

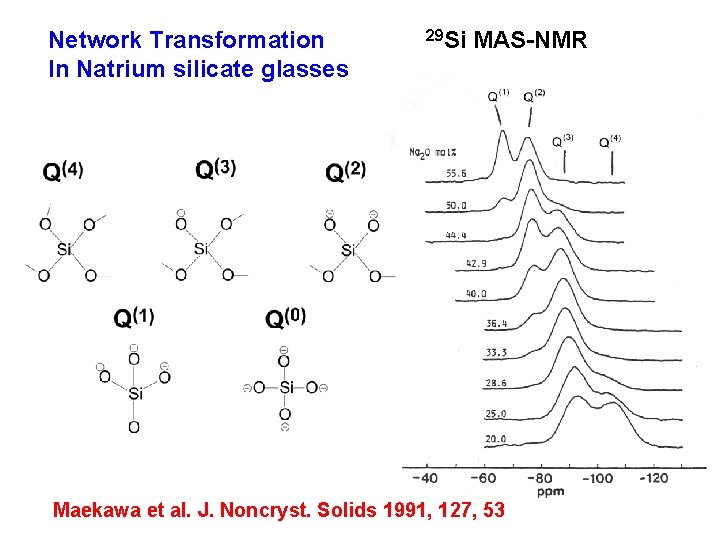
Network Transformation In Natrium silicate glasses 29 Si MAS-NMR Maekawa et al. J. Noncryst. Solids 1991, 127, 53

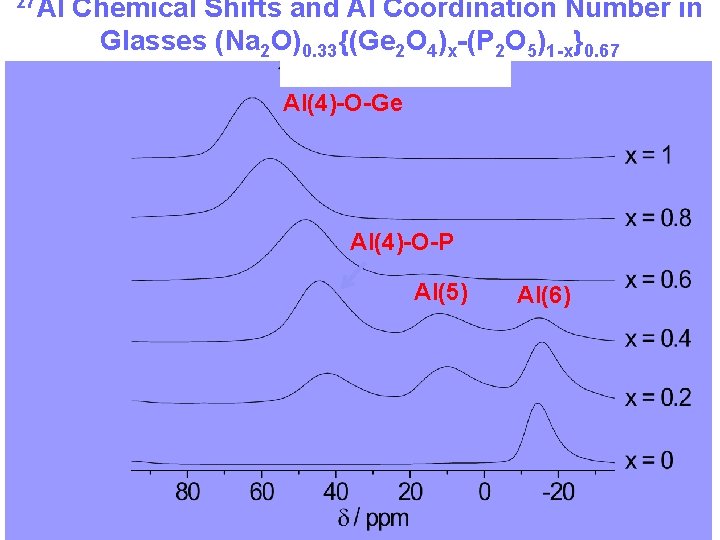
27 Al Chemical Shifts and Al Coordination Number in Glasses (Na 2 O)0. 33{(Ge 2 O 4)x-(P 2 O 5)1 -x}0. 67 Al(4)-O-Ge Al(4)-O-P Al(5) Al(6)

Short Range Order (0. 2 -0. 3 nm) network former network modifier B O M directly bonded neighbors Coordination numbers and symmetries Site quantification MAS-NMR

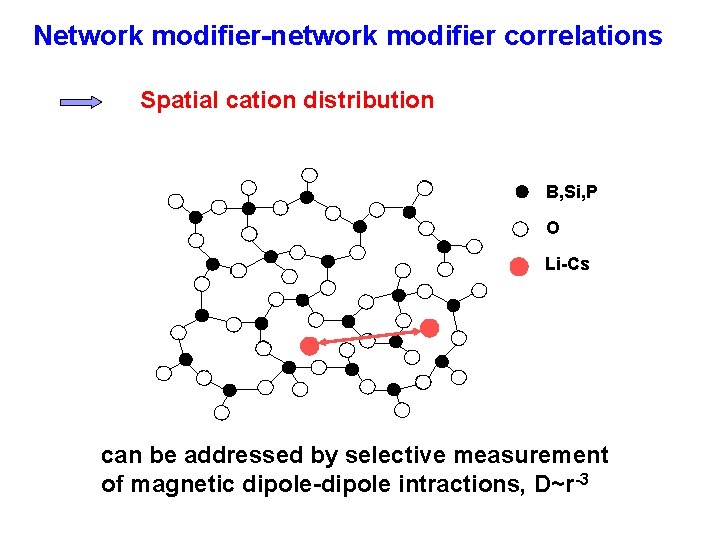
Network modifier-network modifier correlations Spatial cation distribution B, Si, P O Li-Cs can be addressed by selective measurement of magnetic dipole-dipole intractions, D~r-3

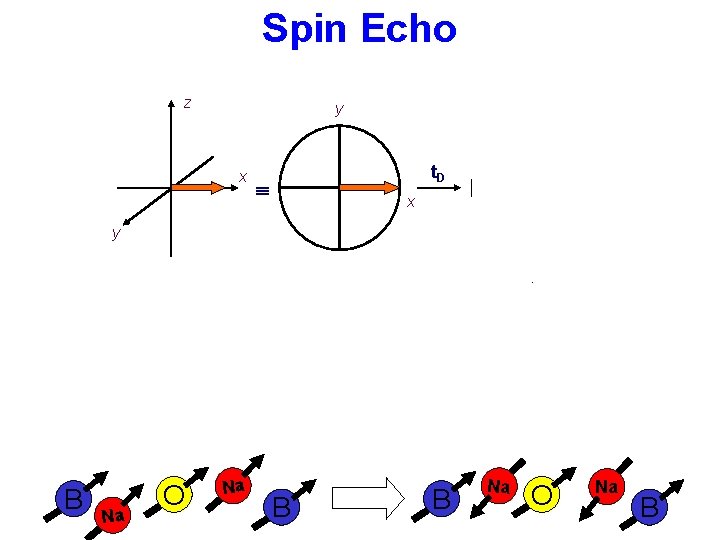
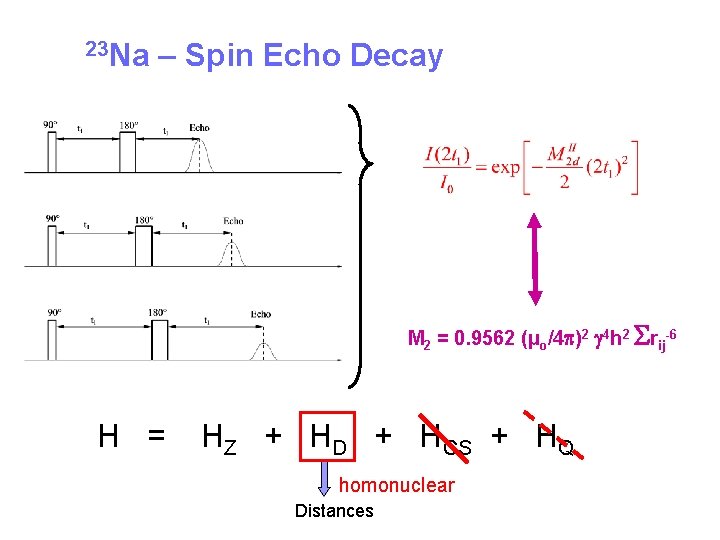
Spin Echo z y x y t. D x x y y dephasing y t. D x x 180 y (or x) refocusing B Na O Na B

23 Na – Spin Echo Decay M 2 = 0. 9562 (µo/4 p)2 g 4 h 2 Srij-6 H = HZ + HD + HCS + HQ homonuclear Distances

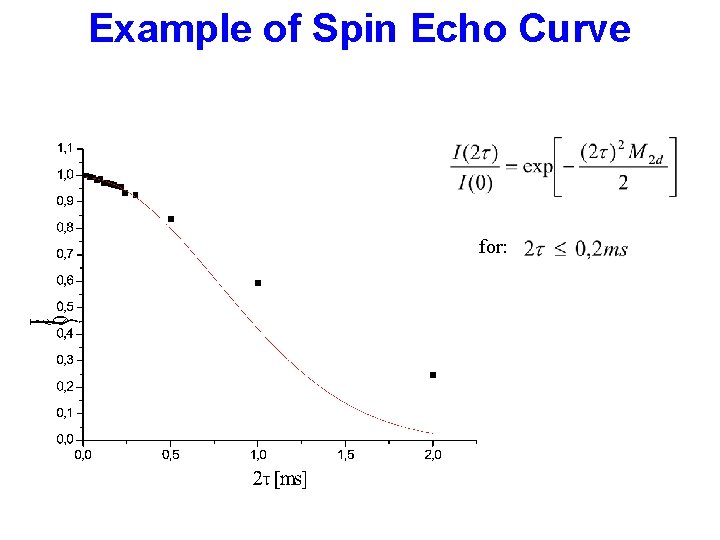
Example of Spin Echo Curve for:

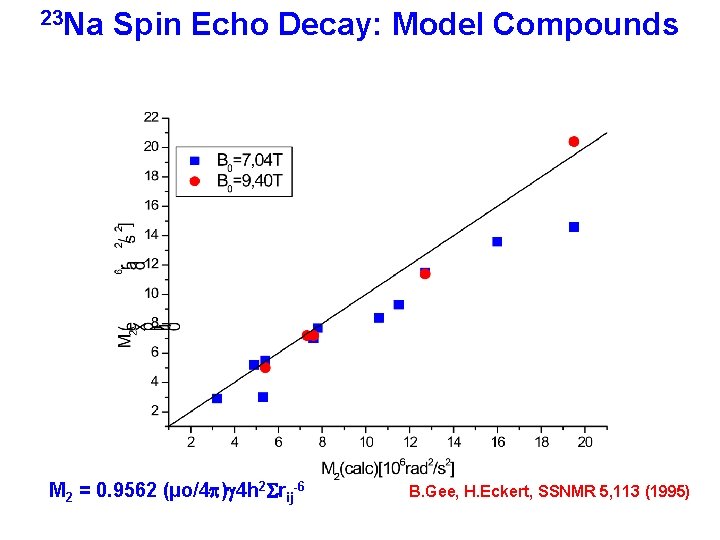
23 Na Spin Echo Decay: Model Compounds M 2 = 0. 9562 (µo/4 p)g 4 h 2 Srij-6 B. Gee, H. Eckert, SSNMR 5, 113 (1995)

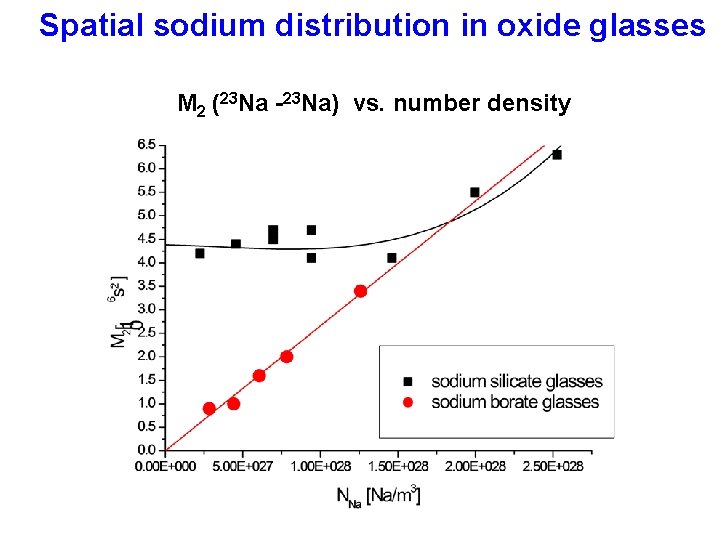
Spatial sodium distribution in oxide glasses M 2 (23 Na -23 Na) vs. number density

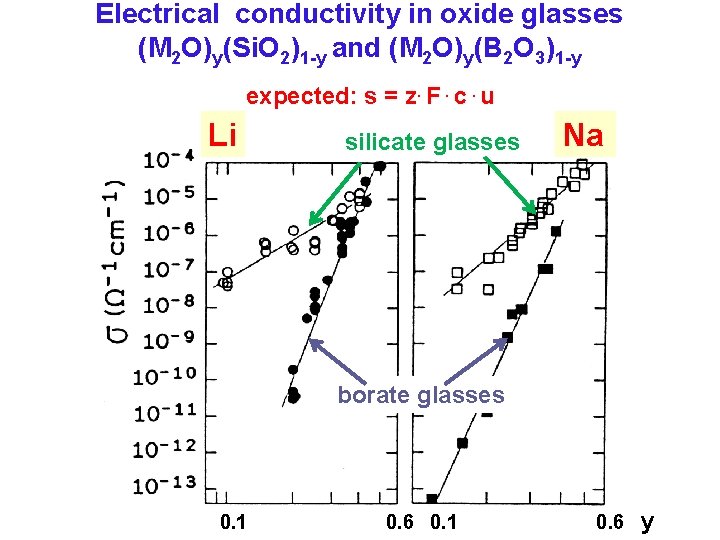
Electrical conductivity in oxide glasses (M 2 O)y(Si. O 2)1 -y and (M 2 O)y(B 2 O 3)1 -y expected: s = z. F. c. u Li silicate glasses Na borate glasses 0. 1 0. 6 y

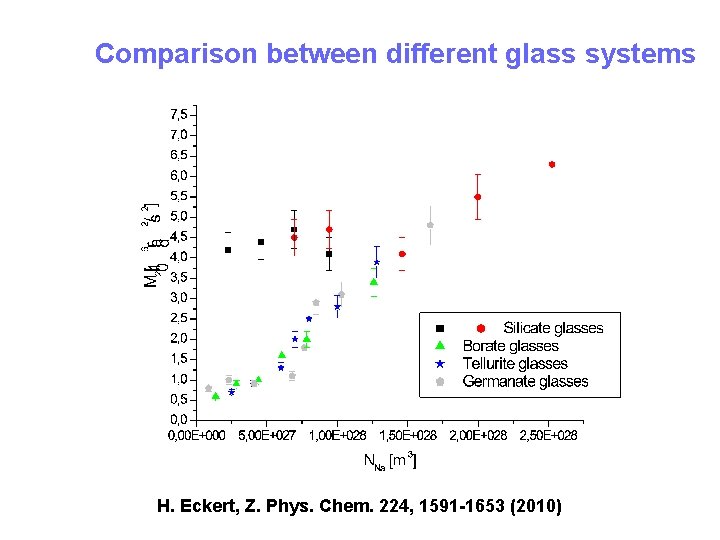
Comparison between different glass systems H. Eckert, Z. Phys. Chem. 224, 1591 -1653 (2010)

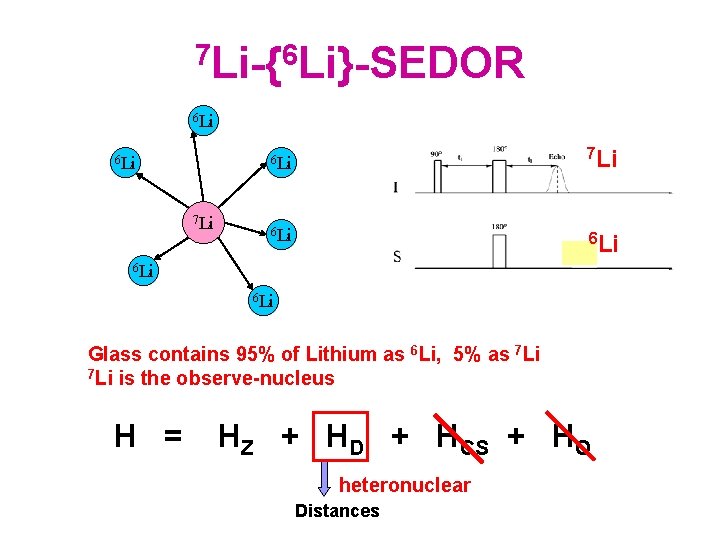
7 Li-{6 Li}-SEDOR 6 Li 7 Li 6 Li 6 Li 6 Li Glass contains 95% of Lithium as 6 Li, 5% as 7 Li is the observe-nucleus H = HZ + HD + HCS + HQ heteronuclear Distances

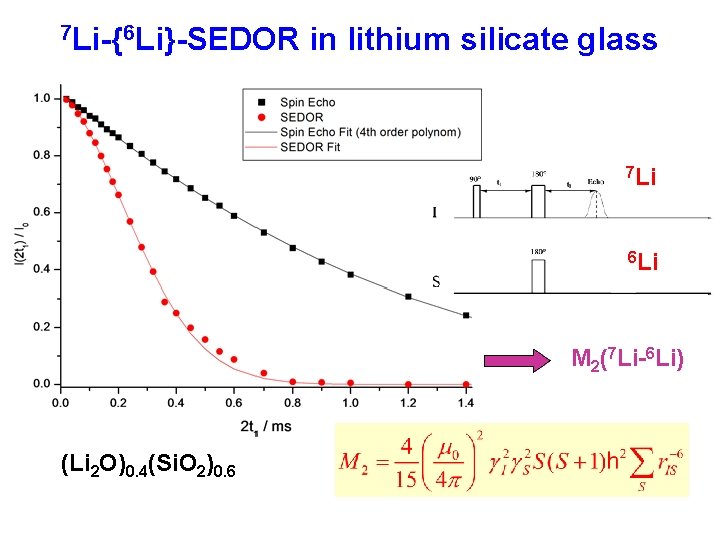
7 Li-{6 Li}-SEDOR in lithium silicate glass 7 Li 6 Li M 2(7 Li-6 Li) (Li 2 O)0. 4(Si. O 2)0. 6

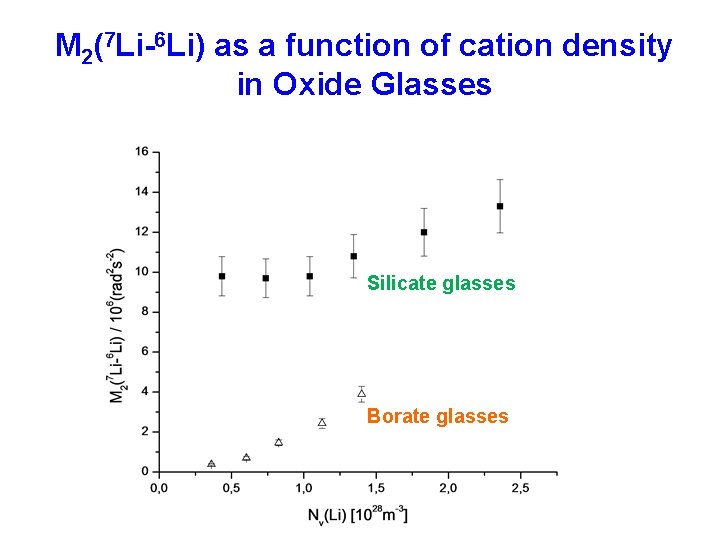
M 2(7 Li-6 Li) as a function of cation density in Oxide Glasses Silicate glasses Borate glasses

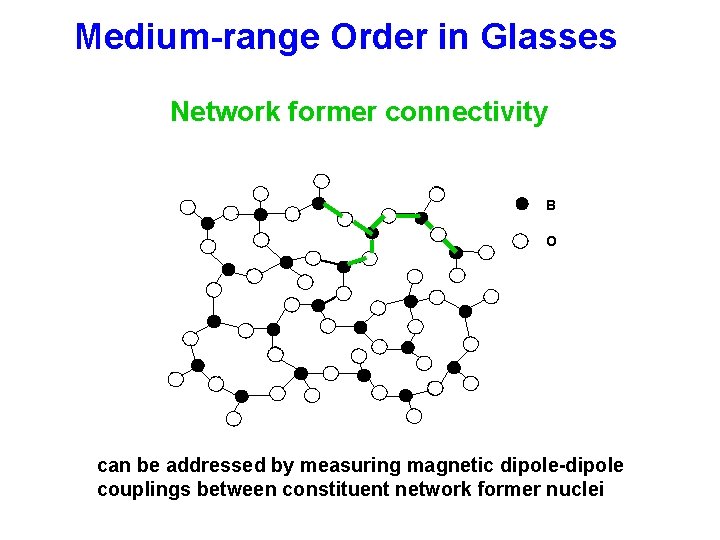
Medium-range Order in Glasses Network former connectivity B O can be addressed by measuring magnetic dipole-dipole couplings between constituent network former nuclei

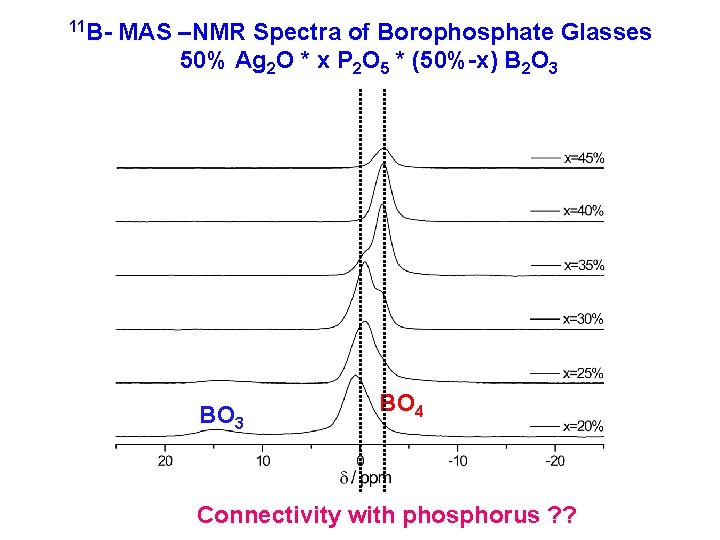
11 B- MAS –NMR Spectra of Borophosphate Glasses 50% Ag 2 O * x P 2 O 5 * (50%-x) B 2 O 3 BO 4 Connectivity with phosphorus ? ?

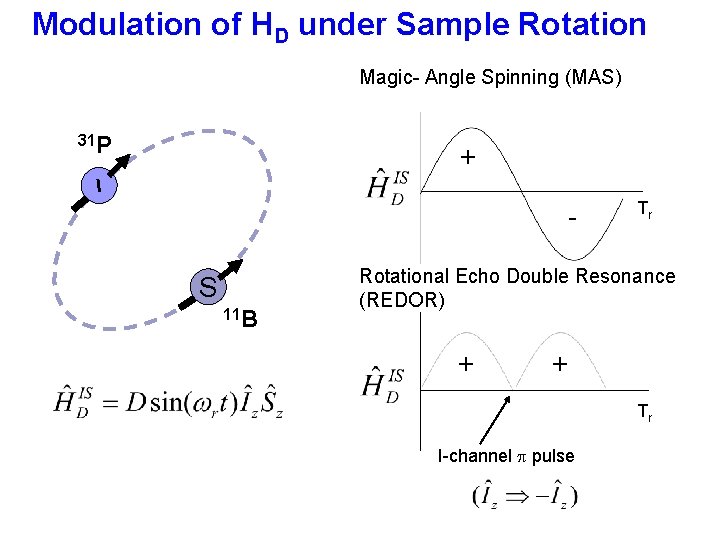
Modulation of HD under Sample Rotation Magic- Angle Spinning (MAS) 31 P + I S 11 B Tr Rotational Echo Double Resonance (REDOR) + + Tr I-channel p pulse

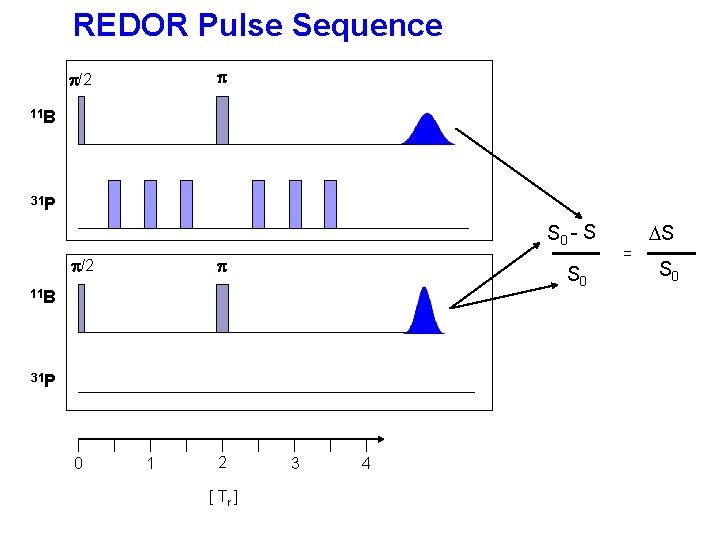
REDOR Pulse Sequence p p/2 11 B 31 P S 0 - S p/2 p S 0 11 B 31 P 0 1 2 [ Tr ] 3 4 = DS S 0

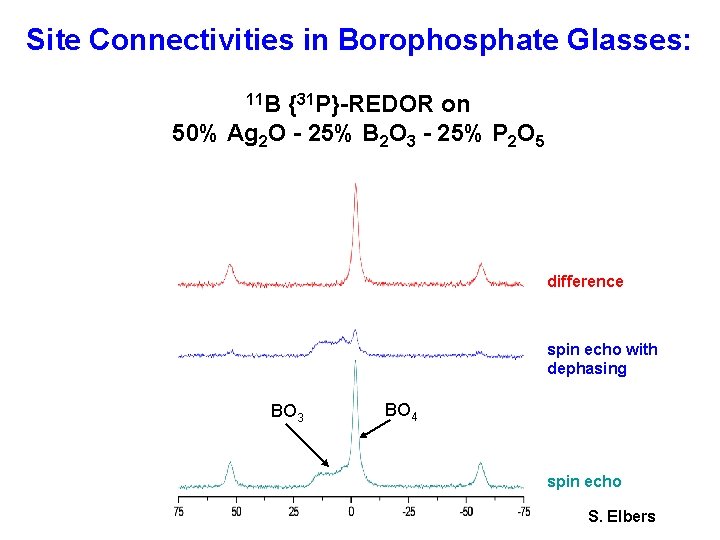
Site Connectivities in Borophosphate Glasses: 11 B {31 P}-REDOR on 50% Ag 2 O - 25% B 2 O 3 - 25% P 2 O 5 difference spin echo with dephasing BO 3 BO 4 spin echo S. Elbers

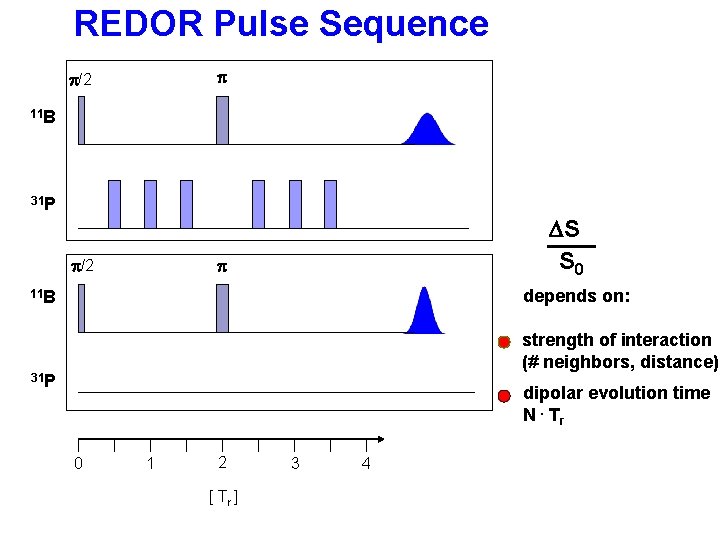
REDOR Pulse Sequence p p/2 11 B 31 P p/2 DS S 0 p depends on: 11 B strength of interaction (# neighbors, distance) 31 P dipolar evolution time N. Tr 0 1 2 [ Tr ] 3 4

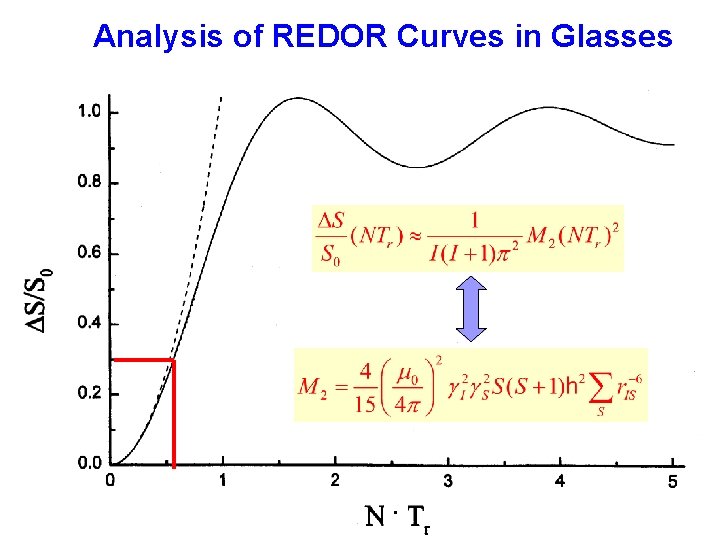
Analysis of REDOR Curves in Glasses .

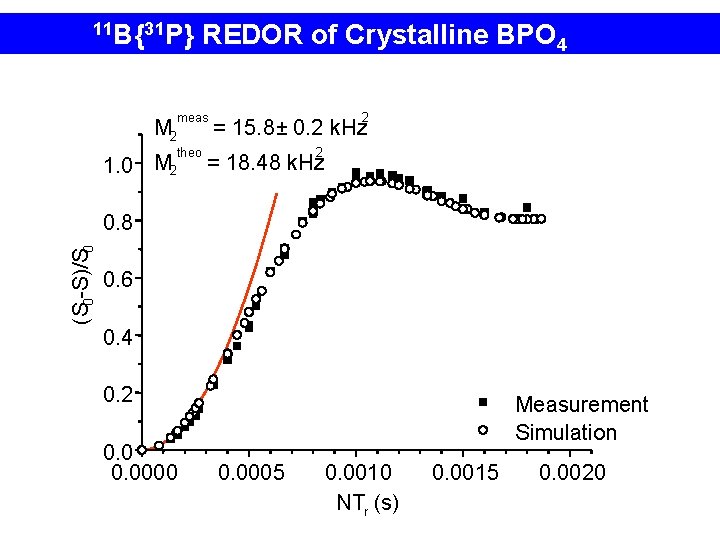
11 B{31 P} REDOR of Crystalline BPO 4 meas M 2 theo 1. 0 M 2 2 = 15. 8 ± 0. 2 k. Hz 2 = 18. 48 k. Hz (S 0 -S)/S 0 0. 8 0. 6 0. 4 0. 2 0. 0000 Measurement Simulation 0. 0005 0. 0010 NTr (s). 0. 0015 0. 0020

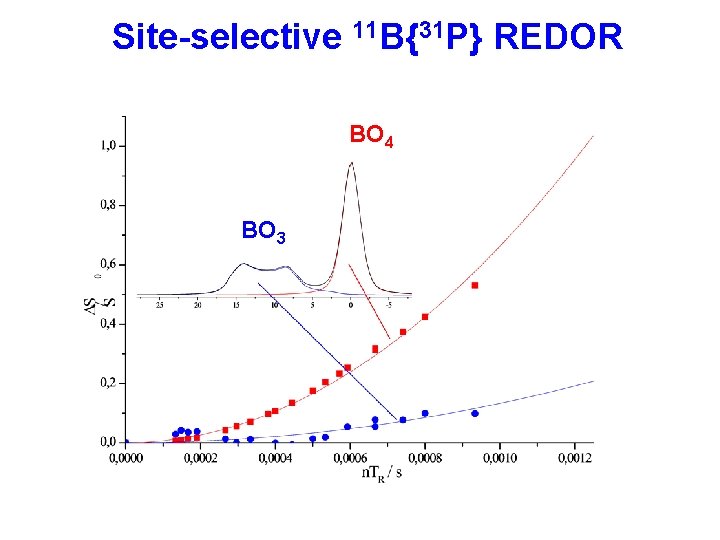
Site-selective 11 B{31 P} REDOR BO 4 BO 3

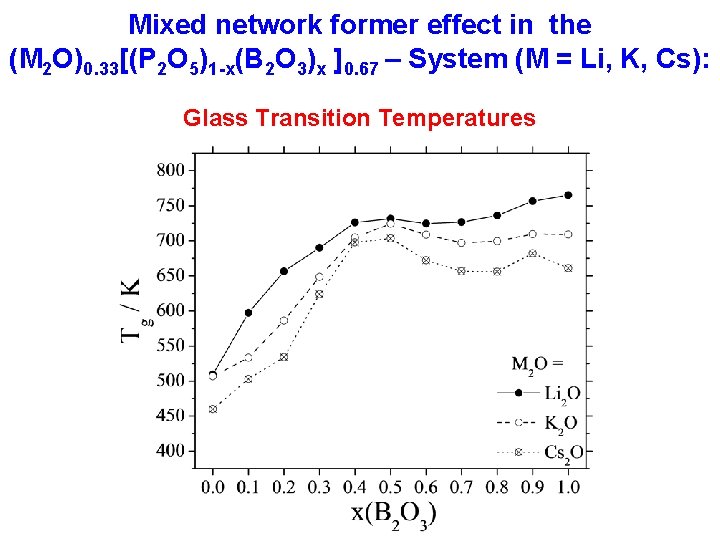
Mixed network former effect in the (M 2 O)0. 33[(P 2 O 5)1 -x(B 2 O 3)x ]0. 67 – System (M = Li, K, Cs): Glass Transition Temperatures

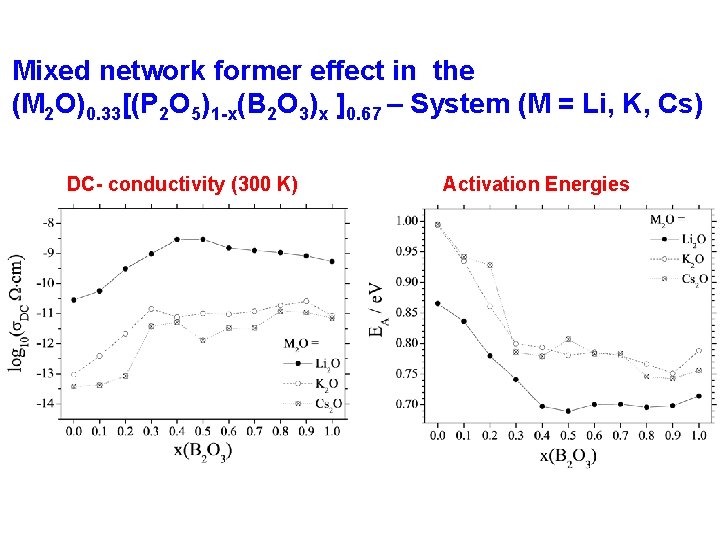
Mixed network former effect in the (M 2 O)0. 33[(P 2 O 5)1 -x(B 2 O 3)x ]0. 67 – System (M = Li, K, Cs) DC- conductivity (300 K) Activation Energies

Structural Issues Regarding the Mixed. Network Former Effect n Network former speciations ¨ Coordination polyhedra ¨ Types of anionic and neutral n Connectivity distributions ¨ Random Linkages ? ¨ Connectivity Preferences ? ¨ Clustering/Phase separation n ? Competition for the network modifier ¨ Proportional n species present sharing vs. preferential attraction Relation to physical properties

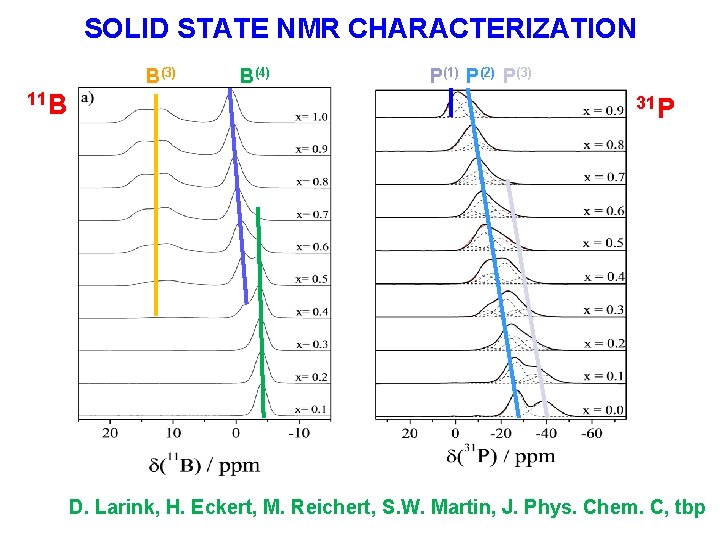
SOLID STATE NMR CHARACTERIZATION B(3) 11 B B(4) P(1) P(2) P(3) 31 P D. Larink, H. Eckert, M. Reichert, S. W. Martin, J. Phys. Chem. C, tbp

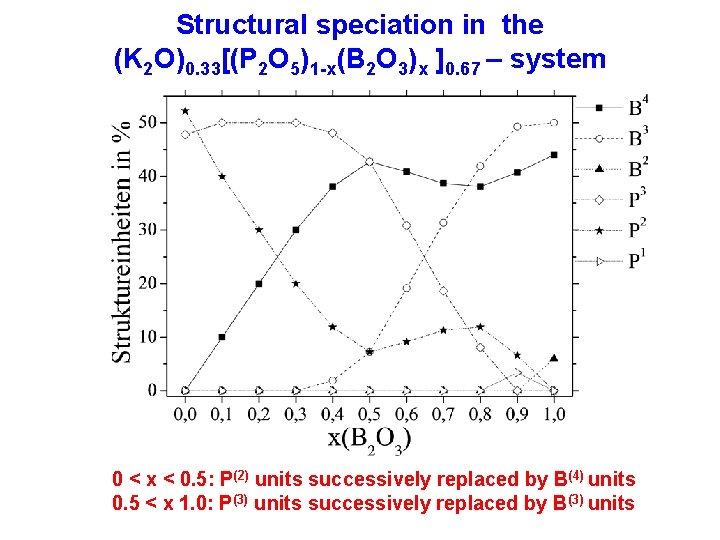
Structural speciation in the (K 2 O)0. 33[(P 2 O 5)1 -x(B 2 O 3)x ]0. 67 – system 0 < x < 0. 5: P(2) units successively replaced by B(4) units 0. 5 < x 1. 0: P(3) units successively replaced by B(3) units

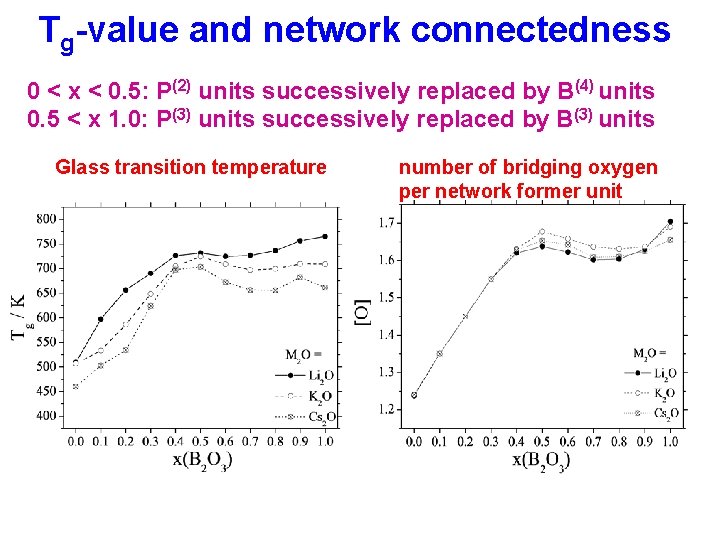
Tg-value and network connectedness 0 < x < 0. 5: P(2) units successively replaced by B(4) units 0. 5 < x 1. 0: P(3) units successively replaced by B(3) units Glass transition temperature number of bridging oxygen per network former unit

Correlation between Tg and [O] (M 2 O)0. 33[(P 2 O 5)1 -x(B 2 O 3)x ]0. 67 (M = Li, K, Cs):

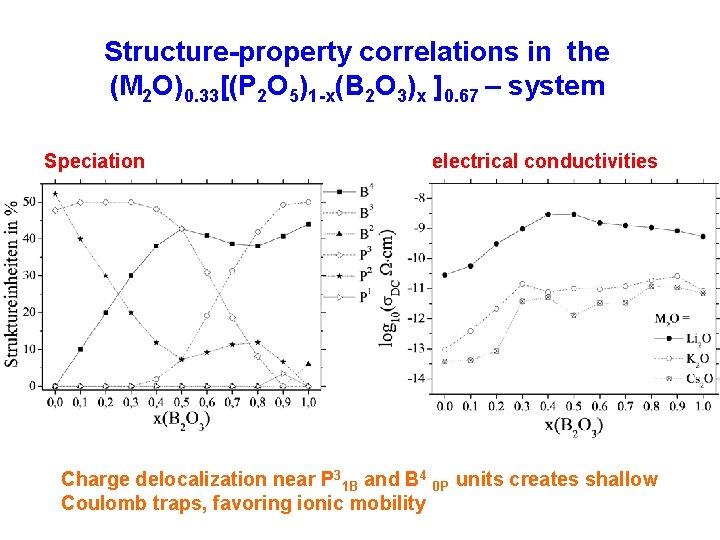
Structure-property correlations in the (M 2 O)0. 33[(P 2 O 5)1 -x(B 2 O 3)x ]0. 67 – system Speciation electrical conductivities Charge delocalization near P 31 B and B 4 0 P units creates shallow Coulomb traps, favoring ionic mobility

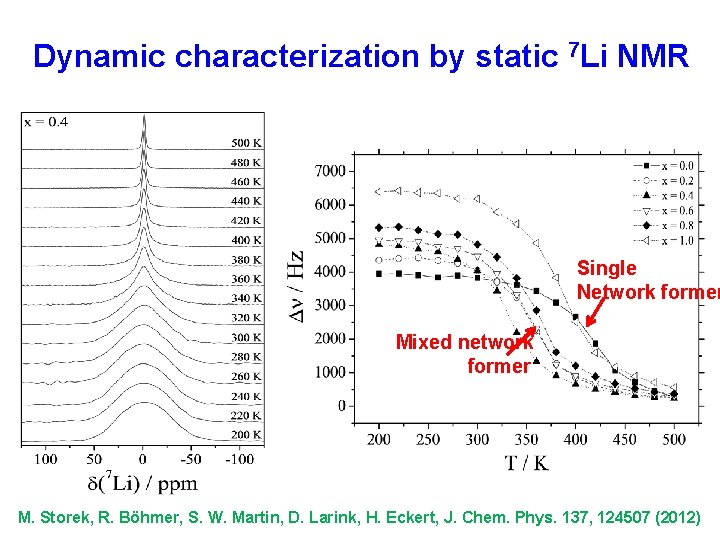
Dynamic characterization by static 7 Li NMR Single Network former Mixed network former M. Storek, R. Böhmer, S. W. Martin, D. Larink, H. Eckert, J. Chem. Phys. 137, 124507 (2012)

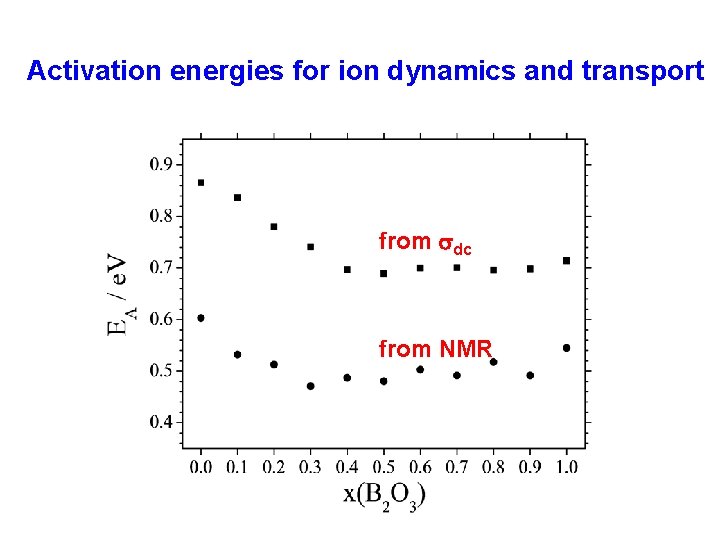
Activation energies for ion dynamics and transport from sdc from NMR

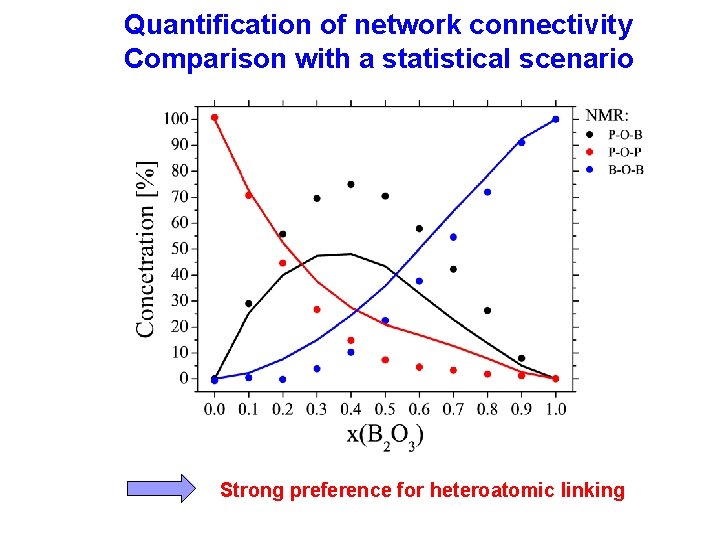
Quantification of network connectivity Comparison with a statistical scenario Strong preference for heteroatomic linking

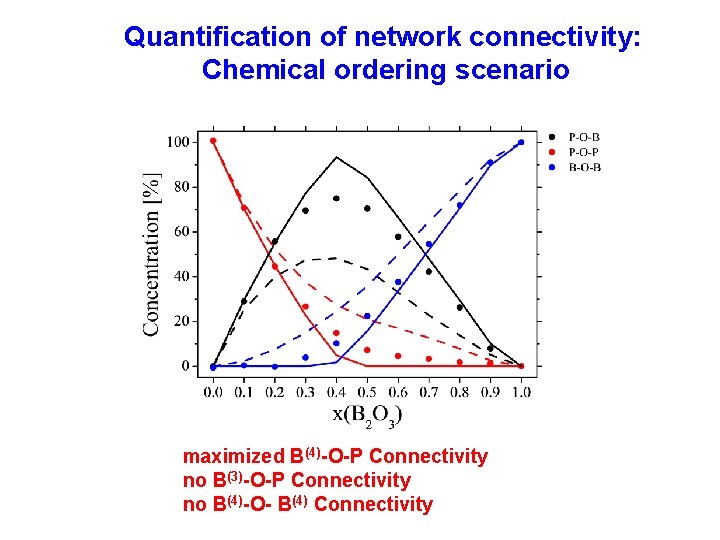
Quantification of network connectivity: Chemical ordering scenario maximized B(4)-O-P Connectivity no B(3)-O-P Connectivity no B(4)-O- B(4) Connectivity

Solid State NMR Periodic Table

Acknowledgments Center for Research, Technology and Education in Vitreous Materials Andrea de Camargo Zanotto Claudio Magon Edgar Ana Candida

Acknowledgments 66 Dr. J. D. Epping (WWU) Dr. Ulrike Voigt (WWU) Dr. S. Elbers (WWU) Dr. S. Puls (WWU) Dr. D. Zielniok (WWU) Dr. Dirk Larink (WWU) Frederik Behrends (WWU) AK Prof. H. Eckert, WWU Münster Prof. Steve W. Martin (Iowa State) R. Moreira (IFSC) Prof. A. S. S. de Camargo (IFSC)