Modern Cryptography The Enigma Machine n n German




















- Slides: 28

Modern Cryptography

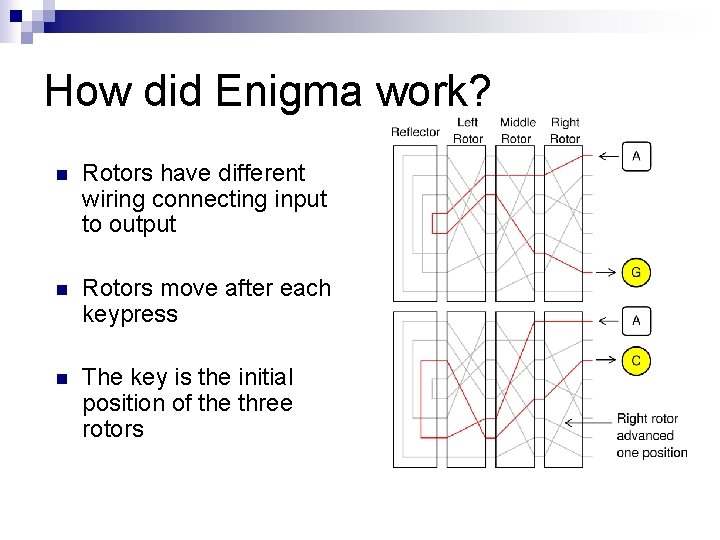
The Enigma Machine n n German encryption and decryption machine used in WWII Essentially a complex, automated substitution cipher

How did Enigma work? n Rotors have different wiring connecting input to output n Rotors move after each keypress n The key is the initial position of the three rotors

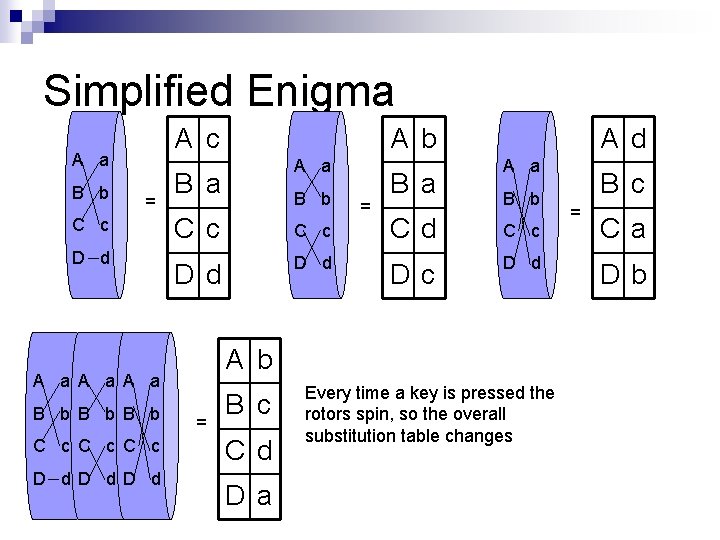
Simplified Enigma A c A a B b = C c D d C c C c D d D d A a B b = B a A d A a B b Cc C c Cd C c Dd D d Dc D d A b A a A a B b B b A b = B c Cd Da Every time a key is pressed the rotors spin, so the overall substitution table changes B c = Ca Db

Breaking the Enigma n n Britain set up its cryptanalysis team in Bletchley Park They consistently broke German codes throughout the war ¨ n Provided the intelligence codenamed ULTRA Important location in the history of computing ¨ ¨ Alan Turing COLOSSUS

Cryptography in the Computer Age n Working with binary instead of letters n We can do things many, many times ¨ Think of an Enigma machine that has 2128 pairs of symbols on each rotor, and 20 rotors n Other than that, the basic principles are the same as classical cryptography

The XOR Operation a b 0 0 1 1 0 1 a b 0 1 1 0 n n e. Xclusive OR “should we go left or right? ” ¨ n Can do one or the other, but not both Useful in cryptography for mixing two binary strings together

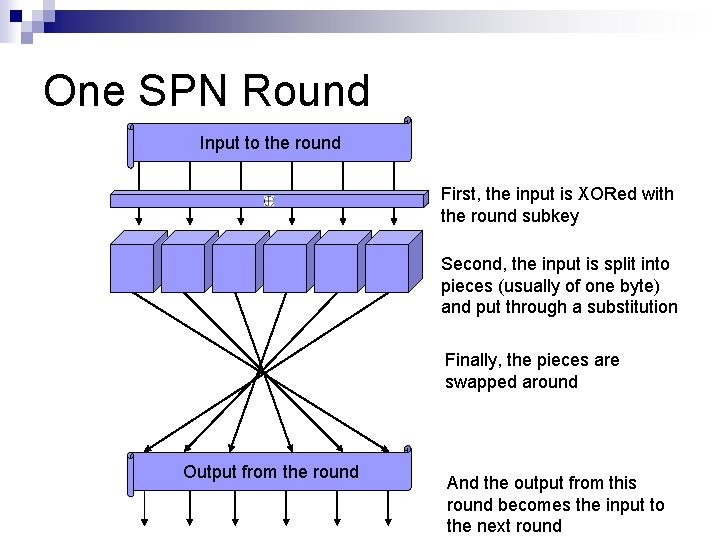
Modern Ciphers n We design one relatively simple scrambling method (called a round) and repeat it many times Think of each round as a rotor on the Enigma ¨ One round may be easy to break, but when you put them all together it becomes very hard ¨ n Almost all ciphers follow one of two structures SPN (Substitution Permutation Network) ¨ Feistel Network ¨ These describe the basic structure of a round ¨

One SPN Round Input to the round First, the input is XORed with the round subkey Second, the input is split into pieces (usually of one byte) and put through a substitution Finally, the pieces are swapped around Output from the round And the output from this round becomes the input to the next round

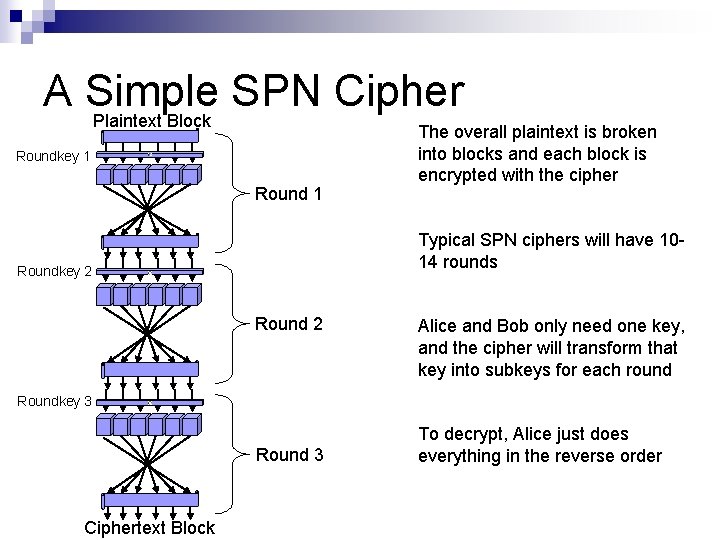
A Simple SPN Cipher Plaintext Block Roundkey 1 Round 1 The overall plaintext is broken into blocks and each block is encrypted with the cipher Typical SPN ciphers will have 1014 rounds Roundkey 2 Round 2 Alice and Bob only need one key, and the cipher will transform that key into subkeys for each round Roundkey 3 Round 3 Ciphertext Block To decrypt, Alice just does everything in the reverse order

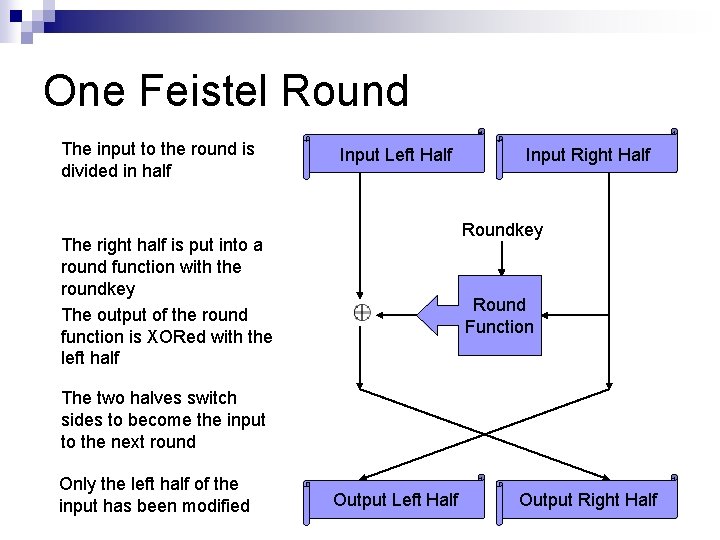
One Feistel Round The input to the round is divided in half Input Left Half Input Right Half Roundkey The right half is put into a round function with the roundkey The output of the round function is XORed with the left half Round Function The two halves switch sides to become the input to the next round Only the left half of the input has been modified Output Left Half Output Right Half

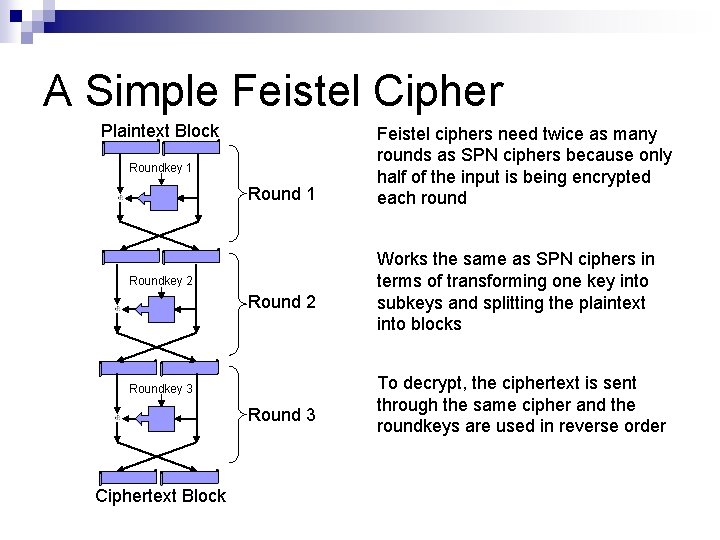
A Simple Feistel Cipher Plaintext Block Roundkey 1 Roundkey 2 Roundkey 3 Round 3 Ciphertext Block Feistel ciphers need twice as many rounds as SPN ciphers because only half of the input is being encrypted each round Works the same as SPN ciphers in terms of transforming one key into subkeys and splitting the plaintext into blocks To decrypt, the ciphertext is sent through the same cipher and the roundkeys are used in reverse order

Modern Ciphers in Practice n Follow SPN/Feistel structure in general, but with added twists for security n There are two important ciphers in the history of modern cryptography ¨ DES (Data Encryption Standard) ¨ AES (Advanced Encryption Standard)

DES n U. S. Government recognized the need to have a standardized cipher for secret documents n DES was developed by IBM in 1976 Feistel structure ¨ Key length of 56 bits, block size of 64 bits ¨ 16 rounds ¨ n Analysis of DES was the beginning of modern cryptographic research

Controversy Surrounding DES n Development process was hidden from public ¨ Suspicions that the government had put in a “backdoor” n Government attempted to shut down research in cryptography

Breaking DES n The key length of DES was too short ¨ If a key is 56 bits long, that means there are 256 possible keys ¨ “DES Cracker” machines were designed to simply brute force all possible keys n People began encrypting the plaintext multiple times with different keys in order to increase the number of keys that need to be checked

Breaking DES cont. n DES was further weakened by the discovery of differential cryptanalysis ¨ ¨ n Ideally a ciphertext should be completely random, there should be no connection to its matching plaintext ¨ ¨ n Biham and Shamir in 1990 The most significant advance in cryptanalysis since frequency analysis Differential analysis exploits the fact that this is never actually the case Uses patterns between plaintext and ciphertext to discover the key There is evidence that IBM knew about differential cryptanalysis back when they were designing DES in 1976

Developing the AES n With DES effectively broken, a new standard was needed n U. S. Government made it an open application/review process this time, and received many submissions n In 2001, after five years, the Rijndael cipher was selected to become the Advanced Encryption Standard

AES (Rijndael) Developed by Vincent Rijmen and Joan Daemen n SPN structure n Block size of 128 bits n Key size of 128, 192, or 256 bits n 10, 12, or 14 rounds depending on the key size n

Current attacks against AES n On AES with 128 -bit keys, a brute force attack would require 2128 work ¨ Any technique that can decrypt a ciphertext with less than 2128 work is considered an attack n Currently the best attacks on AES use variations of differential cryptanalysis ¨ None of them could actually be completed before the sun burns out ¨ None of them work on the full number of rounds

The Problem of Symmetric Key Cryptography n Up until now we’ve been talking about symmetric key cryptography ¨ Alice and Bob are using the same key to encrypt/decrypt n Problem: How does Bob get the key to Alice when Eve is eavesdropping? n Up until 1976 the only solution was to physically give Alice the key in a secure environment

Public Key Cryptography n n n Diffie and Hellman published a paper in 1976 providing a solution We use one key for encryption (the public key), and a different key for decryption (the private key) Everyone knows Alice’s public key, so they can encrypt messages and send them to her ¨ But n only Alice has the key to decrypt those messages No one can figure out Alice’s private key even if they know her public key

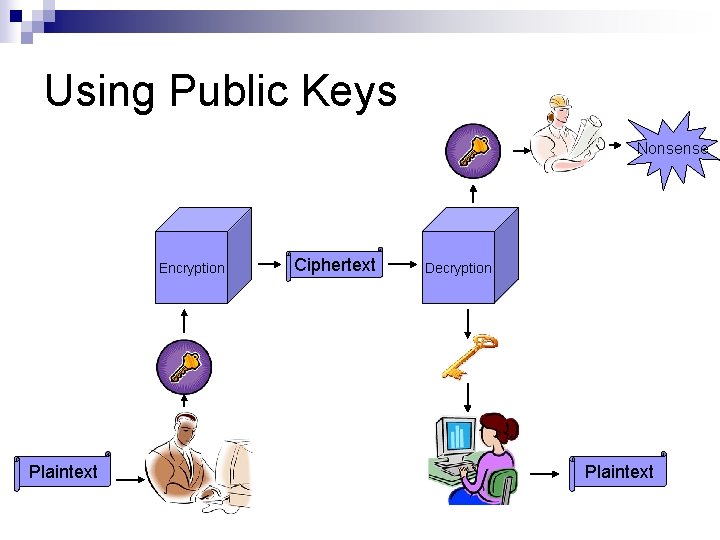
Using Public Keys Nonsense Encryption Plaintext Ciphertext Decryption Plaintext

Public Key Cryptography in Practice n The problem is that public key algorithms are too slow to encrypt large messages ¨ Instead Bob uses public key algorithms to send Alice the symmetric key, and then uses symmetric key algorithms to send the message n Bob and Alice have to be careful when sending these communications back and forth that Eve can’t overhear anything that would allow her to decrypt the message

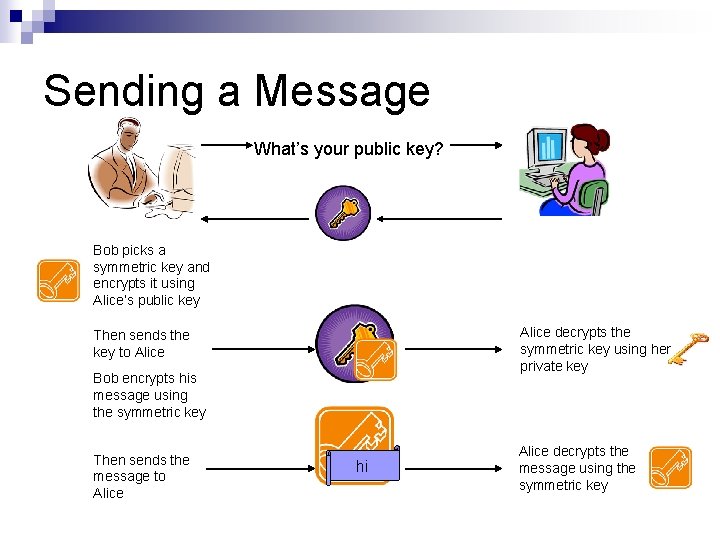
Sending a Message What’s your public key? Bob picks a symmetric key and encrypts it using Alice’s public key Alice decrypts the symmetric key using her private key Then sends the key to Alice Bob encrypts his message using the symmetric key Then sends the message to Alice hi Alice decrypts the message using the symmetric key

The RSA Public Key Cipher n The most popular algorithm is RSA, developed in 1977 ¨ n n Named after its creators: Rivest, Shamir, and Adleman Alice picks two large primes and finds their product She then uses this product to create the public and private keys She sends the product and the public key to Bob, who can use them to encrypt messages Even if Eve knows the product and the public key, she can’t figure out the private key unless she can factor the product ¨ There is no known way to do this efficiently

Are we all secure now? n Unfortunately not, there are still many problems that need to be dealt with ¨ How does Bob know that he’s really talking to Alice? ¨ How does Alice know that the message she receives hasn’t been tampered with? ¨ How does Alice know the message was sent by Bob? n These are questions addressed by other areas of cryptography

The End