Models for Retrieval and Browsing Classical IR Models

Models for Retrieval and Browsing - Classical IR Models Berlin Chen 2004 Reference: 1. Modern Information Retrieval, chapter 2

Index Terms • Meanings From Two Perspectives – In a restricted sense (keyword-based) • An index term is a (predefined) keyword (usually a noun) which has some semantic meaning of its own – In a more general sense (word-based) • An index term is simply any word which appears in the text of a document in the collection • Full-text 2

Index Terms (cont. ) • The semantics (main themes) of the documents and of the user information need should be expressed through sets of index terms – Semantics is lost when expressed through sets of words – Match between the documents and user queries is in the (imprecise? ) space of index terms 3

Index Terms (cont. ) • Documents retrieved are flrequently irrelevant – Since most users have no training in query formation, problem is even worst • Not familar with the underlying IR process • E. g: frequent dissatisfaction of Web users – Issue of deciding document relevance, i. e. ranking, is critical for IR systems 4

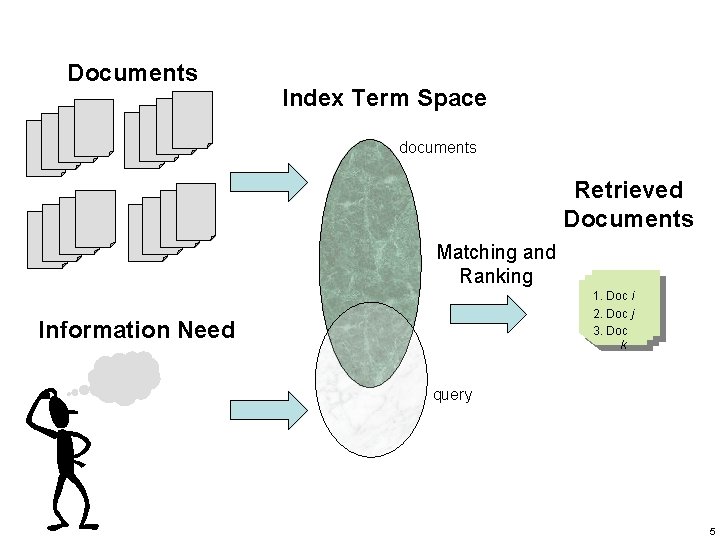
Documents Index Term Space documents Retrieved Documents Matching and Ranking 1. Doc i 2. Doc j 3. Doc k Information Need query 5

Ranking Algorithms • Also called the “information retrieval models” • Ranking Algorithms – Predict which documents are relevant and which are not – Attempt to establish a simple ordering of the document retrieved – Documents at the top of the ordering are more likely to be relevant – The core of information retrieval systems 6

Ranking Algorithms (cont. ) • A ranking is based on fundamental premisses regarding the notion of relevance, such as: – – Common sets of index terms Sharing of weighted terms Likelihood of relevance Concept/semantic matching ? literal-term matching • Distinct sets of premisses lead to a distinct IR models 7

Taxonomy of Classic IR Models • References to the text content – Boolean Model (Set Theoretic) • Documents and queries are represented as sets of index terms – Vector (Space) Model (Algebraic) • Documents and queries are represented as vectors in a tdimensional space – Probabilistic Model (Probabilistic) • Document and query are represented based on probability theory Alternative modeling paradigms will also be extensively studied ! 8

Taxonomy of Classic IR Models (cont. ) • References to the text structure – Non-overlapping list • A document divided in non-overlapping text regions and represented as multiple lists for chapter, sections, subsection, etc. – Proximal Nodes • Define a strict hierarchical index over the text which composed of chapters, sections, subsections, paragraphs or lines 9

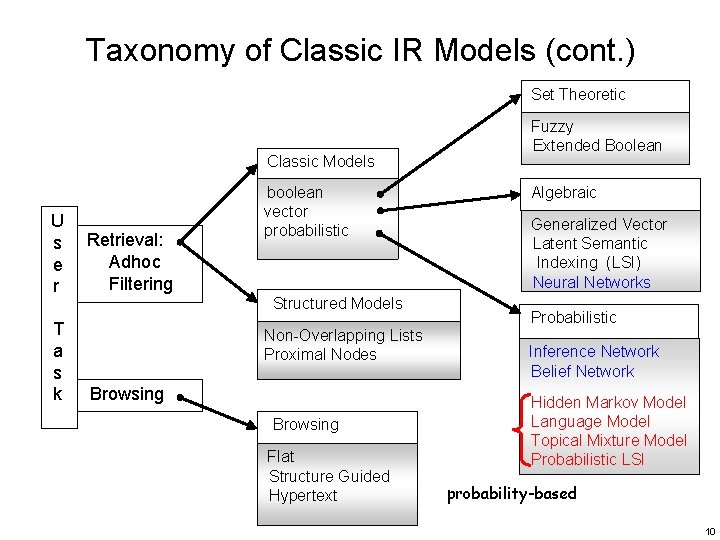
Taxonomy of Classic IR Models (cont. ) Set Theoretic Classic Models U s e r T a s k Retrieval: Adhoc Filtering boolean vector probabilistic Structured Models Non-Overlapping Lists Proximal Nodes Browsing Flat Structure Guided Hypertext Fuzzy Extended Boolean Algebraic Generalized Vector Latent Semantic Indexing (LSI) Neural Networks Probabilistic Inference Network Belief Network Hidden Markov Model Language Model Topical Mixture Model Probabilistic LSI probability-based 10

Taxonomy of Classic IR Models (cont. ) • Three-dimensional Representation • The same IR models can be used with distinct document logical views 11

Browsing the Text Content • Flat/Structure Guided/Hypertext • Example (Spoken Document Retrieval) 12

Browsing the Text Content (cont. ) • Example (Spoken Document Retrieval) 13

Browsing the Text Content (cont. ) • Example (Spoken Document Retrieval) 14

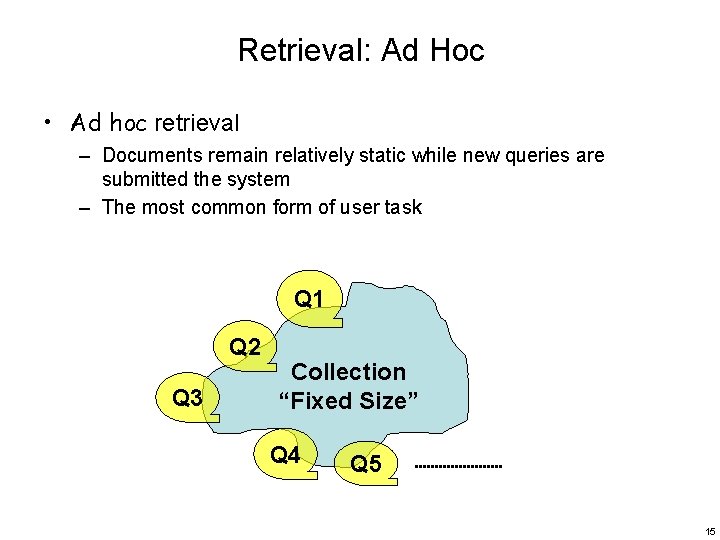
Retrieval: Ad Hoc • Ad hoc retrieval – Documents remain relatively static while new queries are submitted the system – The most common form of user task Q 1 Q 2 Q 3 Collection “Fixed Size” Q 4 Q 5 15

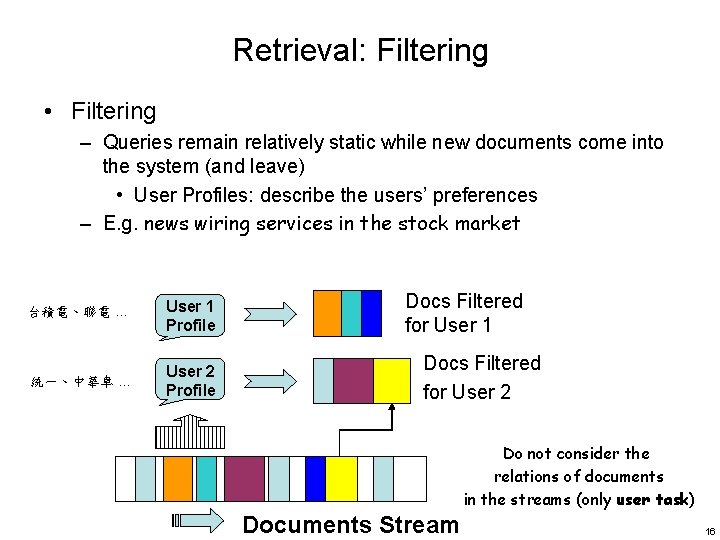
Retrieval: Filtering • Filtering – Queries remain relatively static while new documents come into the system (and leave) • User Profiles: describe the users’ preferences – E. g. news wiring services in the stock market 台積電、聯電 … User 1 Profile 統一、中華車 … User 2 Profile Docs Filtered for User 1 Docs Filtered for User 2 Do not consider the relations of documents in the streams (only user task) Documents Stream 16

Filtering & Routing • Filtering task indicates to the user which document might be interested to him • Determine which ones are really relevant is fully reserved to the user – Documents with a ranking about a given threshold is selected • But no ranking information of filtered documents is presented to user • Routing: a variation of filtering • Ranking information of the filtered documents is presented to the user • The user can examine the Top N documents • The vector model is preferred 17

Filtering: User Profile Construction • Simplistic approach – – Describe the profile through a set of keywords The user provides the necessary keywords User is not involved too much Drawback: If user not familiar with the service (e. g. the vocabulary of upcoming documents) • Elaborate approach – Collect information from user the about his preferences – Initial (primitive) profile description is adjusted by relevance feedback (from relevant/irrelevant information) • User intervention – Profile is continue changing 18

A Formal Characterization of IR Models • The quadruple /D, Q, F, R(qi, dj)/ definition – D: a set composed of logical views (or representations) for the documents in collection – Q: a set composed of logical views (or representations) for the user information needs, i. e. , “queries” – F: a framework for modeling documents representations, queries, and their relationships and operations – R(qi, dj): a ranking function which associations a real number with qi Q and dj D 19

A Formal Characterization of IR Models (cont. ) • Classic Boolean model – Set of documents – Standard operations on sets • Classic vector model – t-dimensional vector space – Standard linear algebra operations on vectors • Classic probabilistic model – Sets (relevant/irrelevant document sets) – Standard probabilistic operations • Mainly the Bayes’ theorem 20

Classic IR Models - Basic Concepts • Each document represented by a set of representative keywords or index terms • An index term is a document word useful for remembering the document main themes • Usually, index terms are nouns because nouns have meaning by themselves – Complements: adjectives, adverbs, amd connectives • However, search engines assume that all words are index terms (full text representation) 21

Classic IR Models - Basic Concepts (cont. ) • Not all terms are equally useful for representing the document contents – less frequent terms allow identifying a narrower set of documents • The importance of the index terms is represented by weights associated to them – Let • ki be an index term • dj be a document • wij be a weight associated with (ki, dj ) • dj=(w 1, j, w 2, j, …, wt, j): an index term vector for the document dj • gi(dj)= wi, j – The weight wij quantifies the importance of the index term for describing the document semantic contents 22

Classic IR Models - Basic Concepts (cont. ) • Correlation of index terms – E. g. : computer and network – Consideration of such correlation information does not consistently improve the final ranking result • Complex and slow operations • Important Assumption/Simplification – Index term weights are mutually independent ! 23

The Boolean Model • Simple model based on set theory and Boolean algebra • A query specified as boolean expressions with and, or, not operations – Precise semantics, neat formalism and simplicity – Terms are either present or absent, i. e. , wij {0, 1} • A query can be expressed as a disjunctive normal form (DNF) composed of conjunctive components – qdnf: the DNF for a query q – qcc: conjunctive components (binary weighted vectors) of qdnf 24

The Boolean Model (cont. ) • For intance, a query [q = ka (kb kc)] can be written as a DNF qdnf=(1, 1, 1) (1, 1, 0) (1, 0, 0) a canonical representation conjunctive components (binary weighted vectors) Ka ka (kb kc) =(ka kb) (ka kc) = (ka kb kc) (ka kb kc) (ka kb kc) => qdnf=(1, 1, 1) (1, 1, 0) (1, 0, 0) Kb (1, 0, 0) (1, 1, 0) (0, 1, 0) (1, 1, 1) (1, 0, 1) (0, 1, 1) (0, 0, 1) Kc 25

The Boolean Model (cont. ) • The similarity of a document dj to the query q sim(dj, q)= 1: if qcc | (qcc qdnf ( ki, gi(dj)=gi(qcc)) 0: otherwise A document is represented as a conjunctive normal form – sim(dj, q)=1 means that the document dj is relevant to the query q – Each document dj can be represented as a conjunctive component 26

Advantages of the Boolean Model • Simple queries are easy to understand relatively easy to implement • Dominant language in commercial (bibliographic) systems until the WWW ka d 9 d 11 cc 3 cc 6 d 5 d 3 d 1 cc 2 0 cc 8 d 2 d 1 cc 5 d 8 cc 1 d 6 cc 4 cc 7 d 7 kc kb d 4 cc 1 = ka kb kc cc 2 = ka kb kc cc 3 = ka kb kc cc 4 = ka kb kc cc 5 = ka kb kc cc 6 = ka kb kc cc 7 = ka kb kc cc 8 = ka kb kc 27

Drawbacks of the Boolean Model • Retrieval based on binary decision criteria with no notion of partial matching (no term weighting) – No notation of a partial match to the query comdition – No ranking (ordering) of the documents is provided (absence of a grading scale) – Term freqency counts in documents not considered – Much more like a data retrieval model 28

Drawbacks of the Boolean Model (cont. ) • Information need has to be translated into a Boolean expression which most users find awkward – The Boolean queries formulated by the users are most often too simplistic (difficult to specify what is wanted) • As a consequence, the Boolean model frequently returns either too few or too many documents in response to a user query 29

The Vector Model • Also called Vector Space Model SMART system Cornell U. , 1968 • Some perspectives – Use of binary weights is too limiting – Non-binary weights provide consideration for partial matches – These term weights are used to compute a degree of similarity between a query and each document – Ranked set of documents provides for better matching for user information need 30

The Vector Model (cont. ) • Definition: – – – wij > =0 whenever ki dj totally t terms in the vocabulary wiq >= 0 whenever ki q document vector dj= (w 1 j, w 2 j, . . . , wtj) query vector q= (w 1 q, w 2 q, . . . , wtq) To each term ki is associated a unitary (basis) vector ui The unitary vectors ui and us are assumed to be orthonormal (i. e. , index terms are assumed to occur independently within the documents) • The t unitary vectors ui form an orthonormal basis for a t -dimensional space – Queries and documents are represented as weighted vectors 31

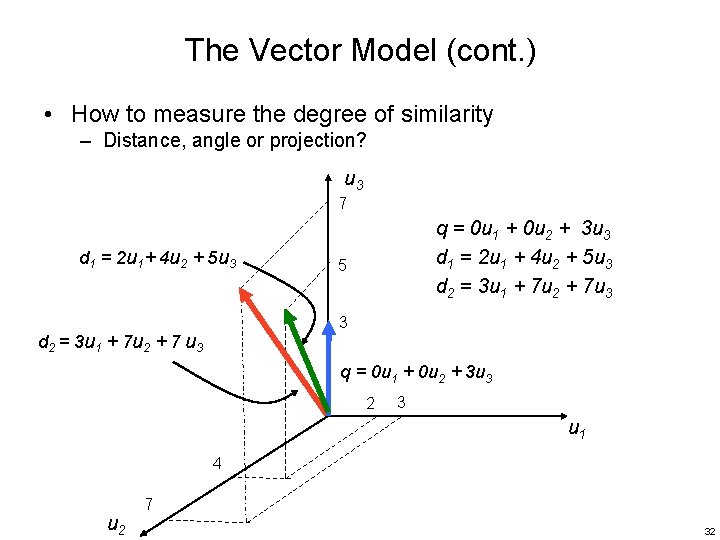
The Vector Model (cont. ) • How to measure the degree of similarity – Distance, angle or projection? u 3 7 d 1 = 2 u 1 + 4 u 2 + 5 u 3 q = 0 u 1 + 0 u 2 + 3 u 3 d 1 = 2 u 1 + 4 u 2 + 5 u 3 d 2 = 3 u 1 + 7 u 2 + 7 u 3 5 3 d 2 = 3 u 1 + 7 u 2 + 7 u 3 q = 0 u 1 + 0 u 2 + 3 u 3 2 3 u 1 4 u 2 7 32

The Vector Model (cont. ) • The similarity of a document dj to the query q y dj q x Document length normalization Won’t affect the final ranking The same for documents, can be discarded (if discarded, equivalent to the projection of the query on the document vector) – Establish a threshold on sim(dj, q) and retrieve documents with a degree of similarity above threshold 33

The Vector Model (cont. ) • Degree of similarity Relevance – Usually, wij > =0 & wiq >= 0 • Cosine measure ranges between 0 and 1 – highly relevant ! – almost irrelevant ! 34

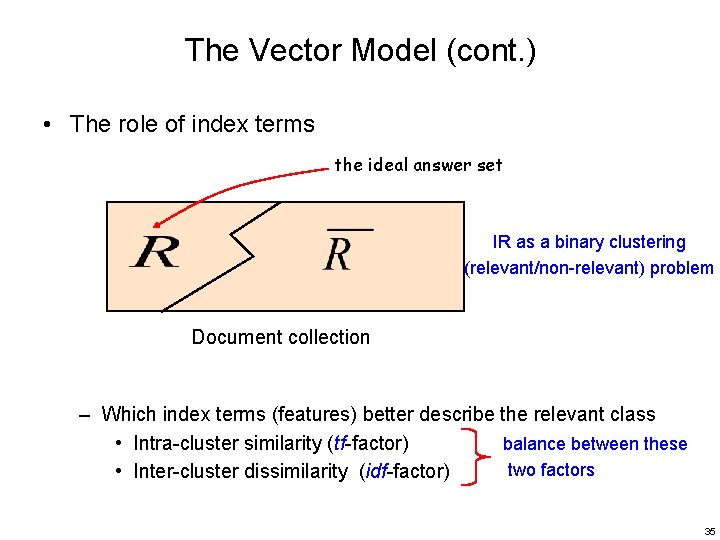
The Vector Model (cont. ) • The role of index terms the ideal answer set IR as a binary clustering (relevant/non-relevant) problem Document collection – Which index terms (features) better describe the relevant class • Intra-cluster similarity (tf-factor) balance between these two factors • Inter-cluster dissimilarity (idf-factor) 35

The Vector Model (cont. ) • How to compute the weights wij and wiq ? • A good weight must take into account two effects: – Quantification of intra-document contents (similarity) • tf factor, the term frequency within a document • High term frequency is needed – Quantification of inter-documents separation (dissi-milarity) • Low document frequency is preferred • idf (IDF) factor, the inverse document frequency – wi, j = tfi, j * idfi 36

The Vector Model (cont. ) • Let, – N be the total number of docs in the collection – ni be the number of docs which contain ki – freqi, j raw frequency of ki within dj • A normalized tf factor is given by – where the maximum is computed over all terms which occur within the document dj 37

The Vector Model (cont. ) • The idf factor is computed as Sparck Jones Document frequency of term ki = – the log is used to make the values of tf and idf comparable. It can also be interpreted as the amount of information associated with the term ki • The best term-weighting schemes use weights which are give by – the strategy is called a tf-idf weighting scheme 38

The Vector Model (cont. ) • For the query term weights, a suggestion is Salton & Buckley • The vector model with tf-idf weights is a good ranking strategy with general collections • The vector model is usually as good as the known ranking alternatives. It is also simple and fast to compute 39

The Vector Model (cont. ) • Advantages – Term-weighting improves quality of the answer set – Partial matching allows retrieval of docs that approximate the query conditions – Cosine ranking formula sorts documents according to degree of similarity to the query • Disadvantages – Assumes mutual independence of index terms • Not clear that this is bad though (? ? ) 40

The Vector Model (cont. ) • Another tf-idf term weighting scheme – For query q Term Frequency Inverse Document Frequency – For document dj 41

The Vector Model (cont. ) • Example k 2 k 1 d 7 d 6 d 2 d 4 d 5 d 1 d 3 k 3 42

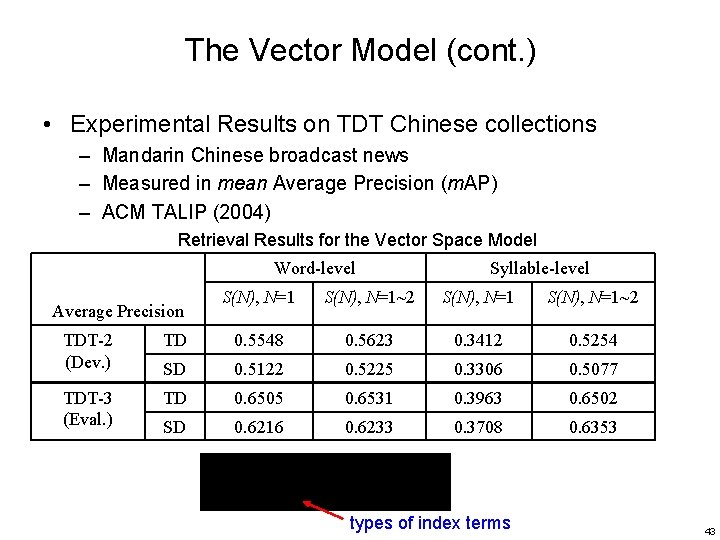
The Vector Model (cont. ) • Experimental Results on TDT Chinese collections – Mandarin Chinese broadcast news – Measured in mean Average Precision (m. AP) – ACM TALIP (2004) Retrieval Results for the Vector Space Model Word-level Average Precision Syllable-level S(N), N=1~2 TDT-2 (Dev. ) TD 0. 5548 0. 5623 0. 3412 0. 5254 SD 0. 5122 0. 5225 0. 3306 0. 5077 TDT-3 (Eval. ) TD 0. 6505 0. 6531 0. 3963 0. 6502 SD 0. 6216 0. 6233 0. 3708 0. 6353 types of index terms 43

The Probabilistic Model Roberston & Sparck Jones 1976 • Known as the Binary Independence Retrieval (BIR) model – “Binary”: all weights of index terms are binary (0 or 1) – “Independence”: index terms are independent ! • Capture the IR problem using a probabilistic framework – Bayes’ decision rule 44

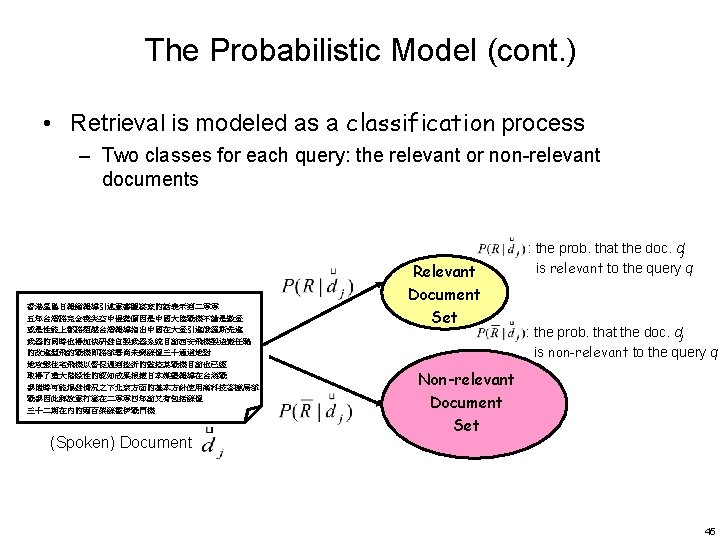
The Probabilistic Model (cont. ) • Given a user query, there is an ideal answer set – The querying process as specification of the properties of this ideal answer set • Problem: what are these properties? – Only the semantics of index terms can be used to characterize these properties • Guess at the beginning what they could be – I. e. , an initial guess for the primimary probabilistis description of ideal answer set • Improve by iterations/interations 46

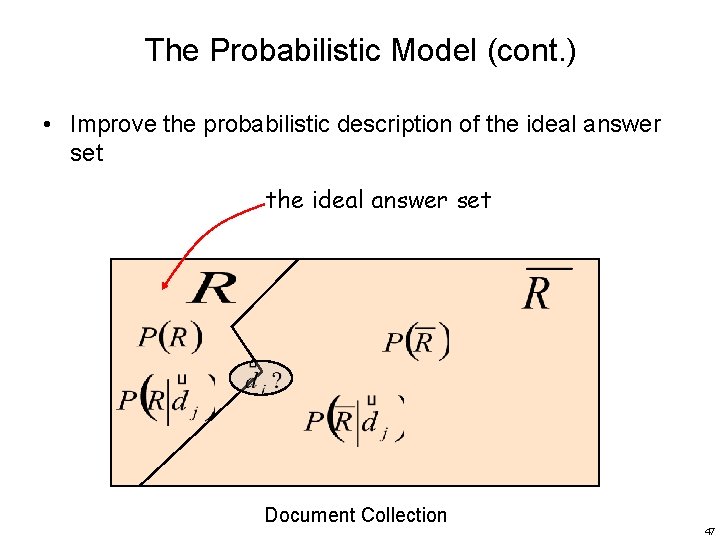
The Probabilistic Model (cont. ) • Improve the probabilistic description of the ideal answer set Document Collection 47

The Probabilistic Model (cont. ) • Given a particular document dj , calculate the probability of belonging to the relevant class, retrieve if greater than probability of belonging to non-relevant class Bayes’ Decision Rule • The similarity of a document dj to the query q Likelihood/Odds Ratio Test The same for all documents Bayes’ Theory 48

The Probabilistic Model (cont. ) • Explanation – : the prob. that a doc randomly selected form the entire collection is relevant – : the prob. that the doc dj is relevant to the query q (selected from the relevant doc set R ) • Further assume independence of index terms : prob. that ki is present in a doc randomly selected form the set R : prob. that ki is not present in a doc randomly selected form the set R 49

The Probabilistic Model (cont. ) • Further assume independence of index terms – Another representation – Take logarithms The same for all documents! 50

The Probabilistic Model (cont. ) • Further assume independence of index terms – Use term weighting wi, q x wi, j to replace gi(dj) Binary weights (0 or 1) are used here is not known at the beginning How to compute and 51

The Probabilistic Model (cont. ) • Initial Assumptions – – : is constant for all indexing terms : approx. by distribution of index terms among all doc in the collection, i. e. the document frequency of indexing term (Suppose that |R|>>|R|, N |R|)) ( : no. of doc that contain . : the total doc no. ) • Re-estimate the probability distributions – Use the initially retrieved and ranked Top V documents : the no. of documents in V that contain ki 52

The Probabilistic Model (cont. ) • Handle the problem of “zero” probabilities – Add constants as the adjust constant – Or use the information of document frequency 53

The Probabilistic Model (cont. ) • Advantages – Documents are ranked in decreasing order of probability of relevance • Disadvantages – Need to guess initial estimates for – All weights are binary: the method does not take into account tf and idf factors – Independence assumption of index terms 54

Brief Comparisons of Classic Models • Boolean model does not provide for partial matches and is considered to be the weakest classic model • Salton and Buckley did a series of experiments that indicated that, in general, the vector model outperforms the probabilistic model with general collections 55