Models for Measuring What do the models have

Models for Measuring

What do the models have in common? l They are all cases of a general model. • How are people responding? • What are your intentions in the analysis? l The items and persons are separable. l They all start with a “number correct” (test) or an “integer score” (Likert scale). • You must have whole-number responses l They do not use a slope parameter • Slopes do not vary from person to person (or item to item) • All person parameters and item parameters are expressed in same scale units.

Dichotomous Model l l Pass / Fail…Right / Wrong…Yes / No One step: Successfully complete it or not : a person’s (n) probability of scoring 1 rather than 0 on item i : ability of person n : difficulty of item i (the step from 0 to 1)

Item Characteristic Curves for Five Dichotomous Items

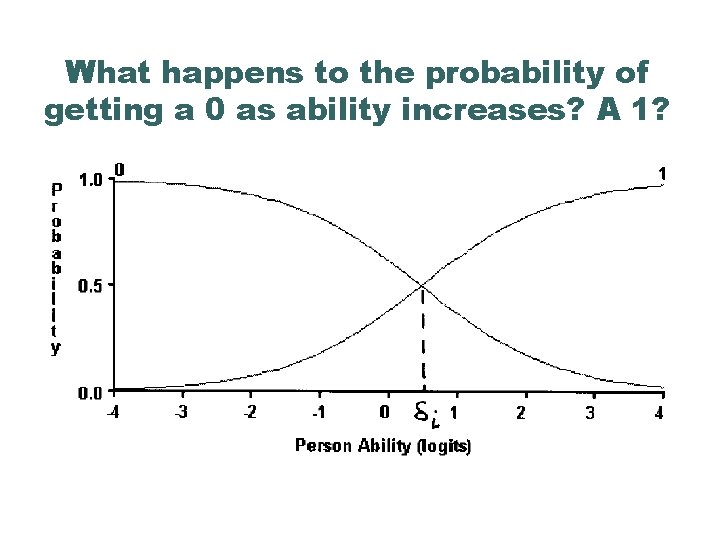
What happens to the probability of getting a 0 as ability increases? A 1?

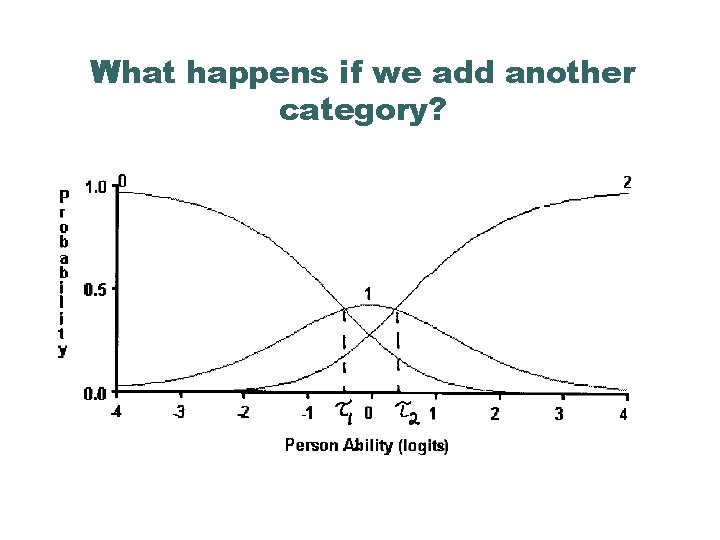
What happens if we add another category?

Interpreting the curves l Between the 0 and 2 curves is the curve which shows the probability of a score of 1. l When a person has very low “ability” relative to the item’s difficulty, the most likely response is 0 l When a person is of moderate “ability” relative to the item’s difficulty, the most likely response is 1 l When a person has an ”ability” much greater than the item’s difficulty, the most likely response is 2.

The τs are Thresholds l Show the points where the probability of a response of either 0 or 1, and 1 or 2 are equally likely. l In the case of a dichotomous response (with two categories), the only threshold is the difficulty, which is the point where the probability of either 0 or 1 is the same. l In the case of three categories there are two thresholds, each of which qualifies the average difficulty of the item.

Rating Scale l Specifies that a set of items share the same rating scale structure. l Originates in attitude surveys where the respondent is presented the same response choices for several items. l When measures are communicated to others, it is impractical to present a different rating scale structure for each item. • Perhaps the audience can comprehend two structures, one for positively worded items and one for negatively worded items.

Rating Scale Model Probability of person n responding in category x to item i. • A position on the variable βn is estimated for each person n • δi is the location of item i on the variable, and τk is the location of the kth step in each item relative to that item’s scale value • m response “thresholds” τ1, τ2, … τm, are estimated for the m+1 rating categories

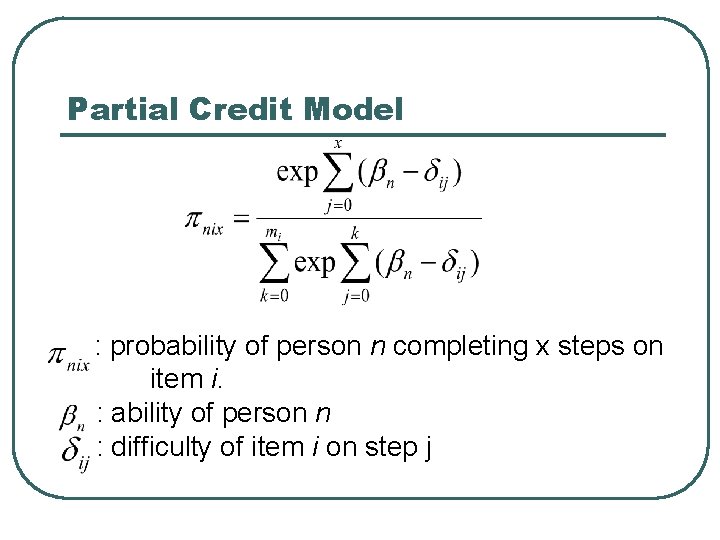
Partial Credit l We can take the second step only if we have successfully completed the first l Responses that are incorrect, but indicate some knowledge, are given partial credit toward a correct response. The amount of partial correctness varies across items. l Response structure and process: the response of one person to one item in one of the categories. l Specifies that each item has its own rating scale structure.

Partial Credit Model : probability of person n completing x steps on item i. : ability of person n : difficulty of item i on step j

Rasch Reliability: “Reproducibility of Relative Measure Location” l High reliability: There is a high probability that persons (or items) estimated with high measures actually do have higher measures than persons (or items) estimated with low measures. l Winsteps reports a “model” and a “real” reliability: • The "model" reliability is an upper bound to this value. • The "real" reliability is a lower bound to this value Raw score-based reliability vs. Measure-based reliability: www. rasch. org/rmt 113 l. htm

Person Reliability l Equivalent to the traditional "test" reliability. l Does your instrument discriminate the sample into enough levels for your purpose? • • l 0. 9 = 3 or 4 levels. 0. 8 = 2 or 3 levels. 0. 5 = 1 or 2 levels Low values indicate a narrow range of person measures OR a small number of items. To Improve person reliability: • Test persons with a wider range of abilities • Lengthen the instrument • Improving the test targeting may help slightly Note: Person reliability is independent of sample size.

Item Reliability l Low reliability means that your sample is not big enough to precisely locate the items on the latent variable. l To improve item reliability: • Increase item difficulty variance • Increase person sample size Note: Item reliability is independent of test length.

What is Separation? l Separation is the number of statistically different performance strata that the test can identify in the sample. l A separation of "2" implies that only two levels of performance can be consistently identified by the test for samples like the one tested. • 0. 95 corresponds to a separation of 4. 5, meaning 4 consistently identifiable strata.

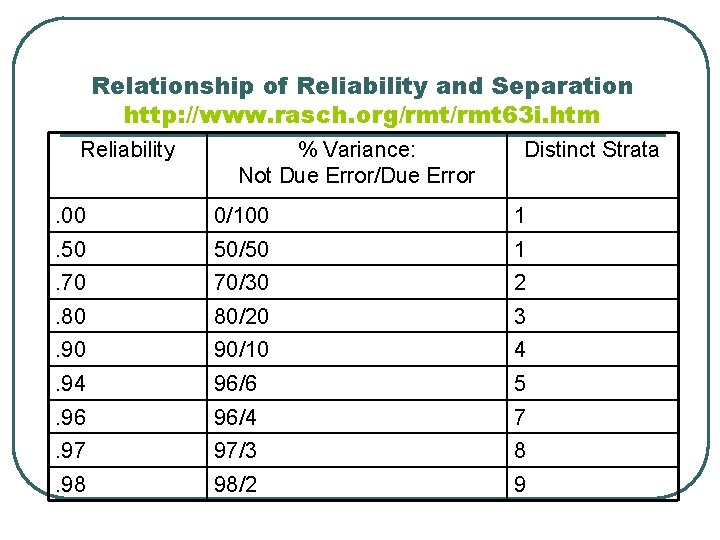
Relationship of Reliability and Separation http: //www. rasch. org/rmt 63 i. htm Reliability % Variance: Not Due Error/Due Error Distinct Strata . 00 0/100 1 . 50 50/50 1 . 70 70/30 2 . 80 80/20 3 . 90 90/10 4 . 94 96/6 5 . 96 96/4 7 . 97 97/3 8 . 98 98/2 9