Models and Security Requirements for IDS Overview Sensitivity

Models and Security Requirements for IDS

Overview • Sensitivity and detection as security requirements for IDS • IDS using the security framework based on sensitivity and detection • Combinatorial tools in intrusion detection

The system and attack model • The model of the system: – Scenario • What are the elements of the network? – Connectivity • How are these elements connected? – Action • What traffic is sent between these elements?

The system and attack model • Scenario – A large network, also called Autonomous System (AS) – AS can have many points of entry, called Border Gateways (BG) of the AS.

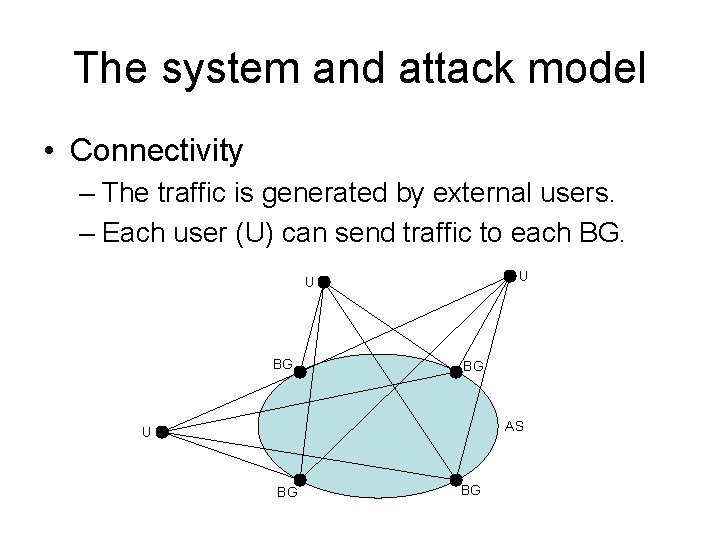
The system and attack model • Connectivity – The traffic is generated by external users. – Each user (U) can send traffic to each BG. U U BG BG AS U BG BG

The system and attack model • Action – The network traffic is a sequence of atomic packets. – The abstraction of a packet: p=(sid, time, poe, pl) sid – the identity of the sender (U) time – a timestamp of the action poe – point of entry (BG) pl – the payload – what is actually sent.

The system and attack model • Action (cont. ) – At any time, the action in an AS is a stream of packets entering AS through any of its BGs. – Each packet in this stream can trigger an event in the AS.

The system and attack model • The model of an attack – Any sequence of c packets, c 1, that successfully alters the state of the nodes (hosts) in an AS in order to achieve a specific (malicious) goal. – Let t be the state of the AS at the time instant t. The state may include, for example: • Available bandwidth • Internal states of all hosts within the AS.

The system and attack model • The model of an attack (cont. ) – We can then define a polynomial time computable predicate (predicates are functions that take binary values) • (1 n, t, t) • n – a security parameter • 1 n – input, unary string of length n

The system and attack model • The model of an attack (cont. ) – Attack • A probability distribution A over all packet sequences ps=(p 1, …, pl) • Samples with this distribution can be obtained efficiently (efficiently samplable distribution) • The probability that the experiment E(A) is unsuccessful is negligible, i. e. smaller than 1/p(n), for all positive polynomials p and all sufficiently large n.

The system and attack model • The model of an attack (cont. ) – Attack (cont. ) • The experiment E(D), for any distribution D: – – A sequence p of packets is drawn from D The sequence p is sent to the network AS turns into the state t The predicate (1 n, t, t) evaluates to the value b {0, 1} • E(D) is successful if b=1.

The system and attack model • The model of an attack (cont. ) – A class of attacks • C={A 1, A 2, …} – Normal traffic distribution • Efficiently samplable probability distribution N over the set of packets, such that the probability that the experiment E(N) is successful is negligible.

The system and attack model • The model of an IDS – An IDS is a triple of algorithms: • A representation algorithm R (data filtering, formatting, feature selection, etc. ) • A data structure algorithm S (data collection, aggregation, knowledge base creation, etc. ) • A classification algorithm C (detection in all forms – pattern-based, rule-based, anomaly-based, response, refinement, information tracing, visualization, etc. )

The system and attack model • The model of an IDS (cont. ) – Two phases in the execution of an IDS: • An initialization phase • A detection phase. – The algorithm S is run in the initialization phase. – The algorithm C is run in the detection phase. – Both S and C use the algorithm R as a subroutine.

The system and attack model • The model of an IDS (cont. ) – In the initialization phase: • The algorithm S uses the algorithm R to process a stream of packet data obtained from normal traffic distributions or known attack distributions. • The output from the algorithm S is a data structure that will be used in the detection phase. • It is assumed that the traffic generated in the initialization phase is not subject to an attack, unless it simulates a known attack.

The system and attack model • The model of an IDS (cont. ) – In the detection phase: • The algorithm C is run on the input data structure and a sequence of traffic packets (possibly subject to a known or a new attack). • It returns an assessment of whether the input sequence of packets contains an attack (and if so whether this attack is new). • The algorithm R maps the sequence of packets entering the AS into a fixed-length tuple having a more compact form (e. g. a point in a highdimensional space)

Security requirements for IDS • Given the following: – A security parameter n – Normal traffic distribution N – (Known) attack distributions A 1, …, At • N, A 1, …, At are efficiently samplable and pairwise disjoint.

Security requirements for IDS • An IDS is a triple of polynomial time algorithms R, S, C such that: – Given a sequence of rw packets p, algorithm R returns a d-tuple r. – Given distributions N, A 1, …, At, algorithm S returns a data structure ds of size at most m[init]. – Given a data structure ds, a sequence m[det] packets p, a detection window dw and a class of attacks C 1, algorithm C returns a classification value out.

Security requirements for IDS • IDS data: rw - representation window • the window of packets used in a single execution of R • usually a small value. m[init] - the length of the stream of packets used in the initialization phase.

Security requirements for IDS • IDS data (cont. ): m[det] - the length of the stream of packets used in the detection phase, to be classified by algorithm S • Considered arbitrarily large, but polynomially dependent on n and rw. dw - Maximum distance between the first and the last packet of an attack sequence within the stream m[det].

Security requirements for IDS • In general, rw, d, m[init], m[det] and dw are all bounded by a polynomial in n. • A typical setting: rw=O(n) d=O(1) m[init]=na m[det]=nb rw dw m[det] a, b>1, potentially large constants.

Security requirements for IDS • An IDS can satisfy two requirements – Sensitivity – Detection

Sensitivity • We would like the output d-tuple of the algorithm R to capture differences between normal traffic and attack traffic. • Capturing these differences is formalized using the notion of computational distinguishability. • We require this distinguishability with respect to a single sample of the distributions, because an attack may be executed only once.

Sensitivity • Informal definition of sensitivity: – A is an attack distribution – N is a normal traffic distribution – The sensitivity of a representation algorithm R is defined on the basis of the distinguishability of the packet streams taken from the distributions A and N.

Sensitivity • Informal definition of sensitivity (cont. ): – The measure of sensitivity is probabilistic: it describes the probability that an attack distribution A can be distinguished from a normal traffic distribution N. • The definition of sensitivity can be generalized to families of distributions.

Detection • The representation algorithm R should give different outputs given fixed-window attack/normal traffic packet streams. • It does not clarify anything about the nature of this difference. • It does not give any constructive algorithm to distinguish which of two different outputs is of which type.

Detection • We would like the algorithms S and C to directly provide “good enough” detection properties on arbitrarily large traffic sequences as long as the algorithm R has “good enough” sensitivity properties on small and fixed traffic sequences.

Detection • The IDS operates in the following way: – In the first phase, the data structure algorithm S is given access to a stream of m packets and can run the representation algorithm on inputs of length rw. – S is allowed to query both the normal traffic distribution N and several (known) attack distributions A 1, …, At. – At the end of the first phase, S returns the data structure ds.

Detection • Operation of the IDS (cont. ): – A sequence of dw packets q is generated and the classification algorithm C returns an output out saying if q contains a sample from one of the known attacks A 1, …, At, or a different (unknown) attack A or no attack at all. – The IDS is successful if this classification is correct.

Detection • Informal definition of detection: – If A is an attack distribution (potentially unknown), the IDS will detect that the given packet sequence q originates from A with probability , for any q. • This definition can also be generalized for classes of attack distributions.

Detection • is always smaller than . • An IDS is considered a “good” detector if is close to . • If A is not distinguishable from N (i. e. =0), then no pair of algorithms S, C can be a detector.

Analysis methodology • An ideal methodology to analyze an IDS would prove that it satisfies: – The sensitivity requirement (for some appropriate parameter values) – The detection requirement (for some appropriate parameter values) under the assumption that it satisfies the sensitivity requirement.

Analysis methodology • A mathematical proof that an IDS satisfies the sensitivity requirement is difficult to obtain, because of the unpredictable nature of a generic unknown attack. • Because of that, validating the sensitivity of the representation algorithm is performed by simulation.

Analysis methodology • Once the sensitivity property is validated for the representation algorithm R, the challenge is to formally prove that the given IDS is a detector.

IDS satisfying the framework • IDS-1 – The algorithm C is based on the approximate nearest neighbour search. • IDS-2 – The algorithm C is based on clustering – allows for more than one distribution for normal traffic – the class of detectable attacks with IDS-2 is larger than that of IDS-1.

IDS satisfying the framework • Approximate nearest neighbour search problem – V is a vector space of dimension d. – is a distance function defined over V. – Given a set Q of k d-component vectors in V, an error parameter and a d-component vector q V, we define the (1+ )-approximate nearest neighbour of q as the vector v in Q such that (q, v) (1+ ) (q, w), for any w Q. – Problem: find the nearest neighbour in Q for any q V.

IDS satisfying the framework • Approximate nearest neighbour search problem (cont. ) – A solution is a pair of algorithms (Init, Search): • On input an k-size set Q of d-length vectors and parameters and , the algorithm Init returns a data structure ds. • On input data structure ds, a vector q and parameter , the algorithm Search returns a vector v. • With probability at least , v Q and v is a (1+ )approximate nearest neighbour of q.

IDS satisfying the framework • Approximate nearest neighbour search problem (cont. ) – The algorithm Init must run in time polynomial in k and d. – The algorithm Search must run in time polynomial in d and log k. – Init is used in the initialization phase (off-line). – Search is used in the detection phase (on-line). – Such algorithms Init and Search exist.

Combinatorial tools in ID • We would like to have an IDS with arbitrary detection window. • We start with IDS 1=(R 1, S 1, C 1) with the representation window rw 1 and detection window dw 1=k. • IDS 1 with its level of sensitivity can detect attacks having l effective packets.

Combinatorial tools in ID • We construct IDS 2=(R 2, S 2, C 2) from IDS 1, with representation window rw 2 and detection window dw 2=m. • This can be done by means of a covering set system (l, k, m) – a combinatorial object.

Combinatorial tools in ID • Covering set system (covering design) – l, k, m – positive integers. – S – a set of cardinality m. – T={T 1, …, Ts} – a set of subsets of S of cardinality k. – T is an (l, k, m)-covering set system for S if for any Si S of cardinality l, there exists a subset Tj T such that Si Tj.

Combinatorial tools in ID • Covering set system (cont. ) – Space efficiency of the covering set system T is the cardinality s of T (can be a function of l, k, m). – Time efficiency of T is the running time (as a function of l, k, m) that an algorithm takes to construct T.

Combinatorial tools in ID • Starting from IDS 1=(R 1, S 1, C 1) with representation window rw 1 and detection window dw 1=k and given an (l, k, m)-covering set system for S={1, …, m} with time efficiency t and space efficiency s, it is possible to construct IDS 2=(R 2, S 2, C 2) with rw 2=rw 1 and dw 2=m, for any m polynomial in k, where C 2 runs in time O(t+s time(C 1)). • R 2=R 1, S 2=S 1.

Further reading • G. Di Crescenzo, A. Ghosh, R. Talpade, Towards a Theory of Intrusion Detection, Proceedings of ESORICS 2005, LNCS 3679, pp. 267 -286, 2005.