Modelo Linear Geometria Aspectos bsicos 1 NADA SUBSTITUI

Modelo Linear : Geometria + Aspectos básicos 1
NADA SUBSTITUI A LEITURA DOS “CLÁSSICOS” SEJA EFICAZ ESTUDE ESTA LIÇÃO ANTES DE “ABRIR O LIVRO”. MELHORARÁ O SEU RENDIMENTO E GANHARÁ TEMPO mas… 2

3
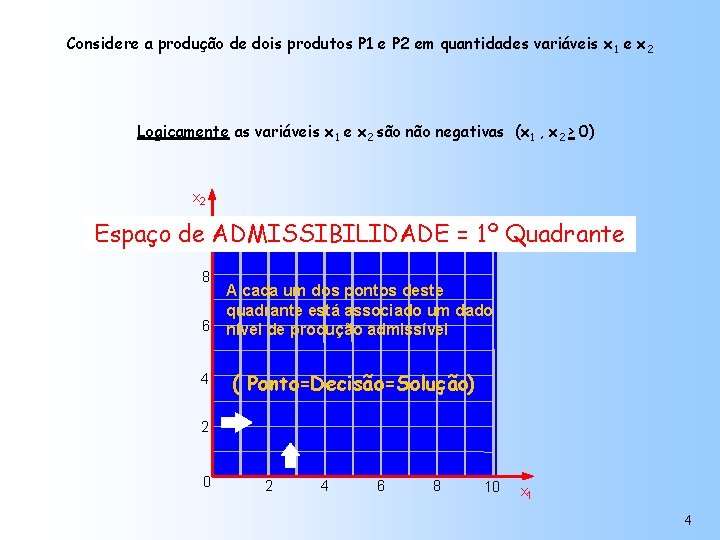
Considere a produção de dois produtos P 1 e P 2 em quantidades variáveis x 1 e x 2 Logicamente as variáveis x 1 e x 2 são negativas (x 1 , x 2 > 0) x 2 Espaço de 10 ADMISSIBILIDADE = 1º Quadrante 8 A cada um dos pontos deste quadrante está associado um dado 6 nível de produção admissível 4 ( Ponto=Decisão=Solução) 2 0 2 4 6 8 10 x 1 4
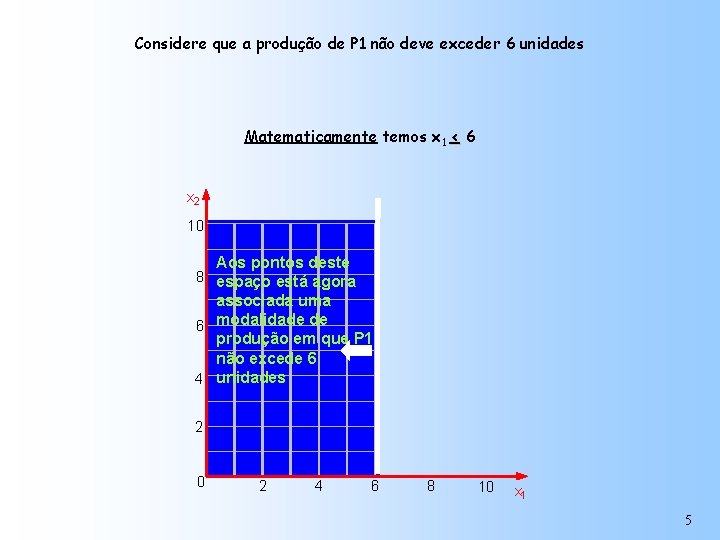
Considere que a produção de P 1 não deve exceder 6 unidades Matematicamente temos x 1 < 6 x 2 10 Aos pontos deste 8 espaço está agora associada uma 6 modalidade de produção em que P 1 não excede 6 4 unidades 2 0 2 4 6 8 10 x 1 5
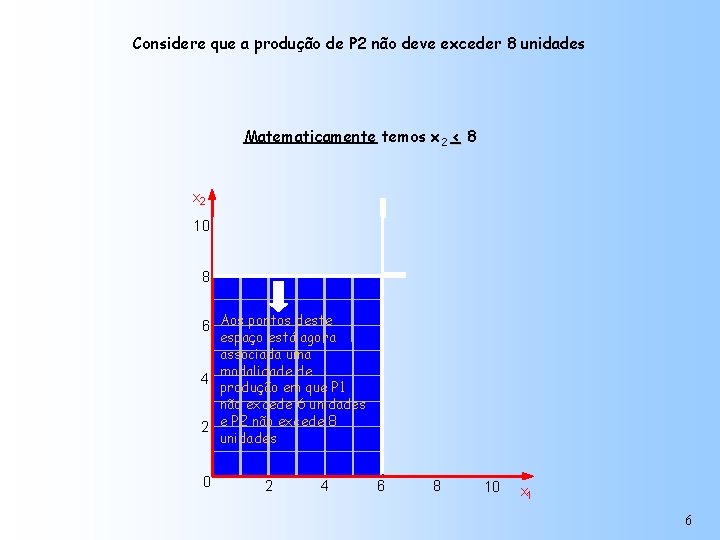
Considere que a produção de P 2 não deve exceder 8 unidades Matematicamente temos x 2 < 8 x 2 10 8 6 Aos pontos deste espaço está agora associada uma modalidade de 4 produção em que P 1 não excede 6 unidades 2 e P 2 não excede 8 unidades 0 2 4 6 8 10 x 1 6
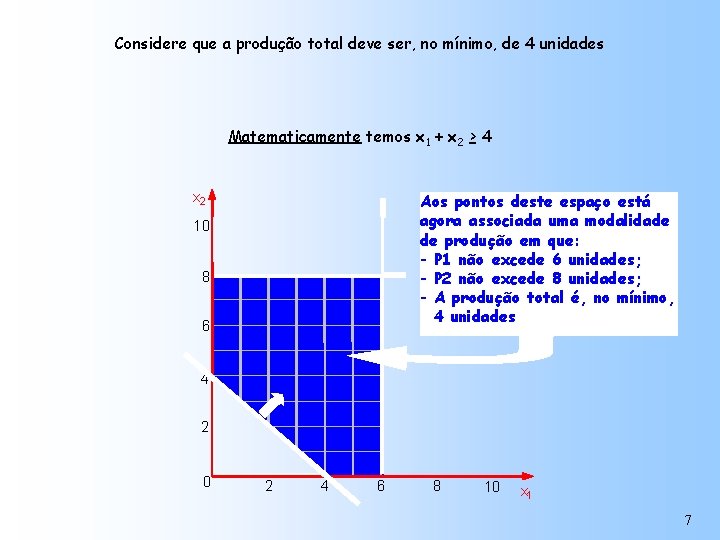
Considere que a produção total deve ser, no mínimo, de 4 unidades Matematicamente temos x 1 + x 2 > 4 x 2 Aos pontos deste espaço está agora associada uma modalidade de produção em que: - P 1 não excede 6 unidades; - P 2 não excede 8 unidades; - A produção total é, no mínimo, 4 unidades 10 8 6 4 2 0 2 4 6 8 10 x 1 7
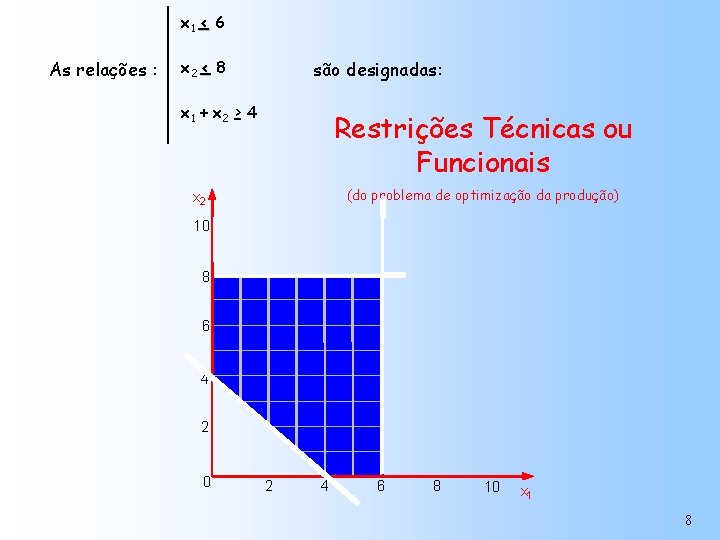
x 1 < 6 As relações : x 2 < 8 são designadas: x 1 + x 2 > 4 Restrições Técnicas ou Funcionais (do problema de optimização da produção) x 2 10 8 6 4 2 0 2 4 6 8 10 x 1 8
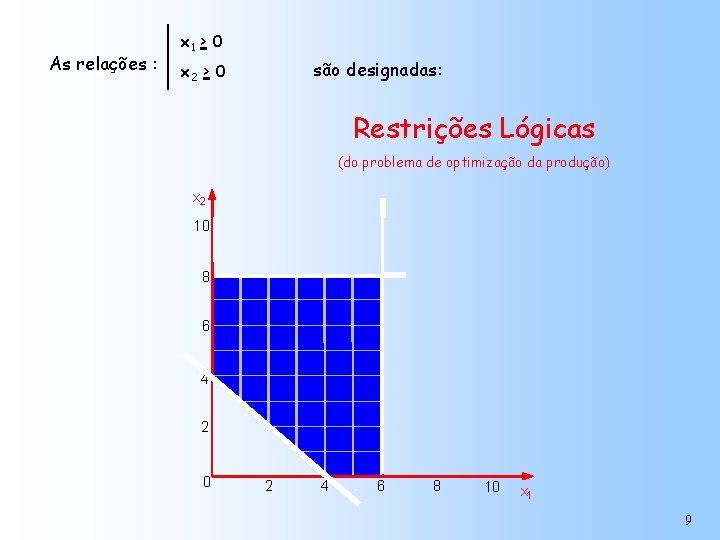
As relações : x 1 > 0 são designadas: x 2 > 0 Restrições Lógicas (do problema de optimização da produção) x 2 10 8 6 4 2 0 2 4 6 8 10 x 1 9
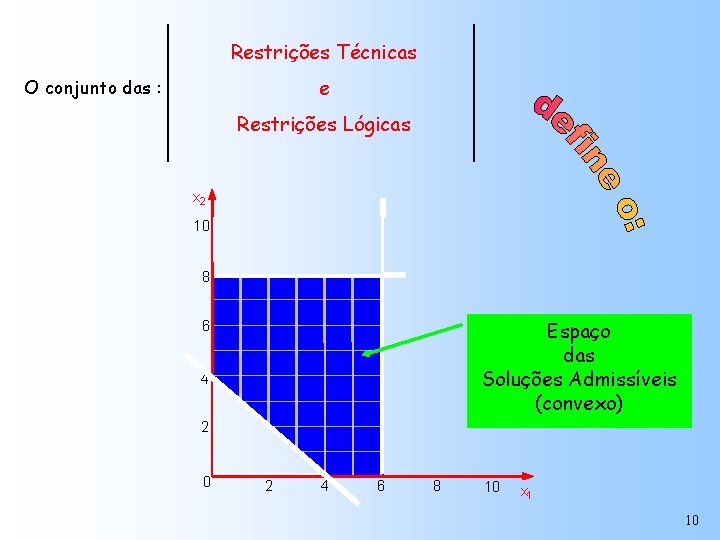
Restrições Técnicas e O conjunto das : Restrições Lógicas x 2 10 8 Espaço das Soluções Admissíveis (convexo) 6 4 2 0 2 4 6 8 10 x 1 10
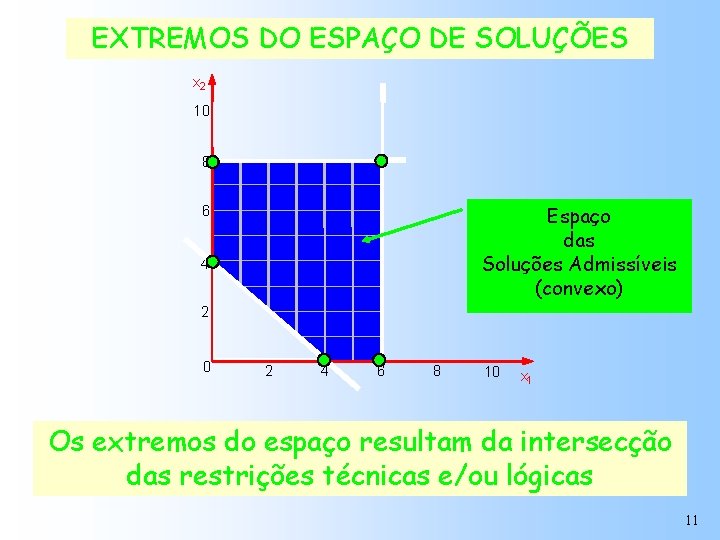
EXTREMOS DO ESPAÇO DE SOLUÇÕES x 2 10 8 Espaço das Soluções Admissíveis (convexo) 6 4 2 0 2 4 6 8 10 x 1 Os extremos do espaço resultam da intersecção das restrições técnicas e/ou lógicas 11
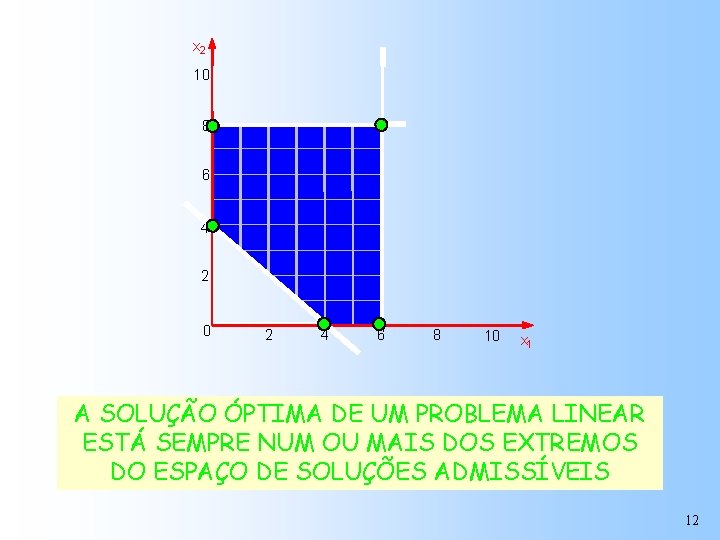
x 2 10 8 6 4 2 0 2 4 6 8 10 x 1 A SOLUÇÃO ÓPTIMA DE UM PROBLEMA LINEAR ESTÁ SEMPRE NUM OU MAIS DOS EXTREMOS DO ESPAÇO DE SOLUÇÕES ADMISSÍVEIS 12
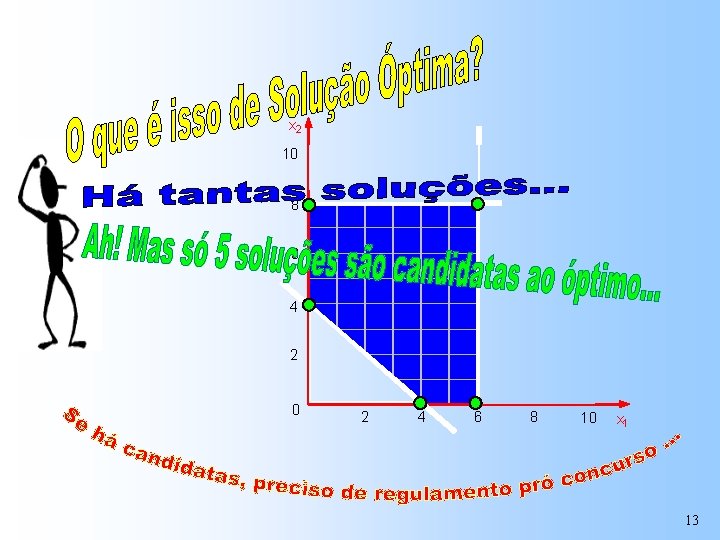
x 2 10 8 6 4 2 0 2 4 6 8 10 x 1 13

Considere que a venda dos produtos P 1 e P 2 é feita, respectivamente, com margens de lucro de 3 e 5 € por unidade vendida 14

Considere que a venda dos produtos P 1 e P 2 é feita, respectivamente, com margens de lucro de 3 e 5 € por unidade vendida 3 x 1 + 5 x 2 Max f(X)=3 x 1 + 5 x 2 15

e… temos o Modelo de Programação Linear para optimizar a produção de P 1 e P 2 … Max f(X)=3 x 1 + 5 x 2 (lucro a maximizar) sujeito a: x 1 < 6 (produção de P 1 não deve exceder 6 unidades) x 2 < 8 (produção de P 2 não deve exceder 8 unidades) x 1 + x 2 > 4 (produção total mínima de 4 unidades) x 1 , x 2 > 0 (não negatividade) 16

Componentes do Modelo de PL § Uma função – Função Objectivo – para Maximizar ou Minimizar § Exº: Maximizar lucro, produção, contribuição § Exº: Minimizar custo, espaço usado, tempo necessário § Um conjunto de variáveis reais – Variáveis de Decisão § Exº: Níveis de produção § Exº: Matéria prima a adquirir § Um conjunto de restrições – Restrições Técnicas e Lógicas – aos valores das variáveis de decisão § Exº: Não produzir menos do que 0 unidades de um produto § Exº: Não utilizar mais do que 500 horas de trabalho 17
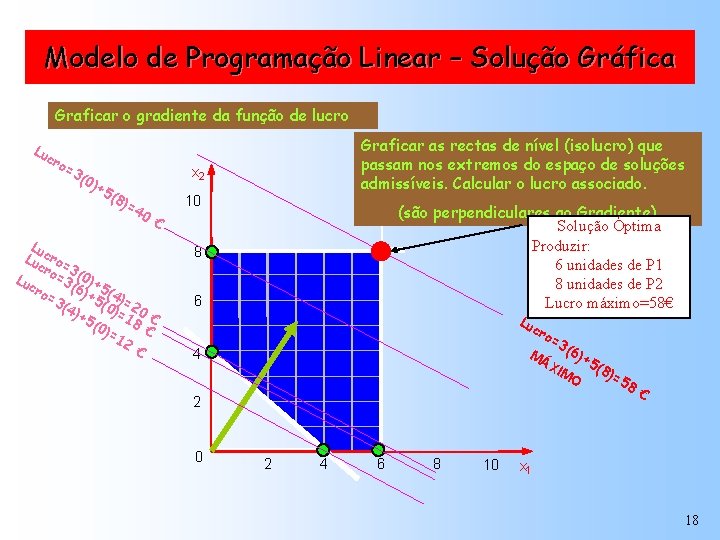
Modelo de Programação Linear – Solução Gráfica Graficar o gradiente da função de lucro Lu cr o= 3( 0) +5 (8 )= 4 Graficar as rectas de nível (isolucro) que passam nos extremos do espaço de soluções admissíveis. Calcular o lucro associado. x 2 0 10 (são perpendiculares ao Gradiente) Solução Óptima Produzir: 6 unidades de P 1 8 unidades de P 2 Lucro máximo=58€ € Lu Lu cro= cr 3 Lu o=3( (0)+ cr o= 6)+55(4) 3( (0 =2 4) +5 )=180 € (0 € )= 12 € 8 6 Lu cr o= 3 MÁ (6)+ XIM 5(8 )= O 4 58 2 0 2 4 6 8 10 € x 1 18

19
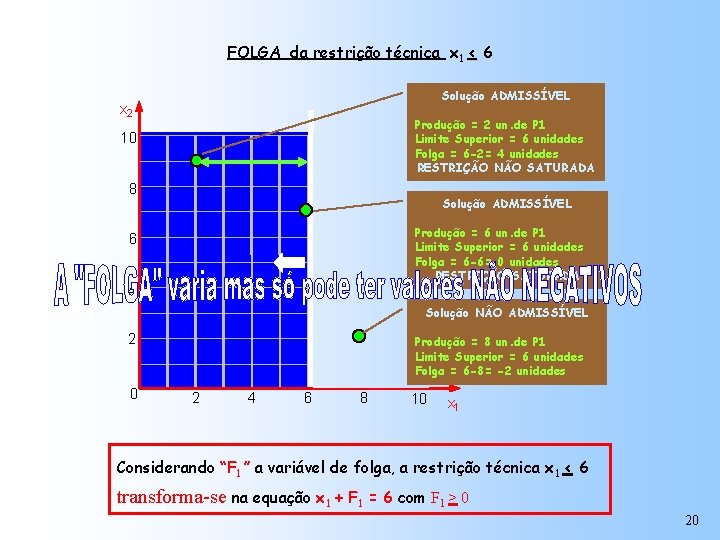
FOLGA da restrição técnica x 1 < 6 Solução ADMISSÍVEL x 2 Produção = 2 un. de P 1 Limite Superior = 6 unidades Folga = 6 -2= 4 unidades RESTRIÇÃO NÃO SATURADA 10 8 Solução ADMISSÍVEL Produção = 6 un. de P 1 Limite Superior = 6 unidades Folga = 6 -6= 0 unidades RESTRIÇÃO SATURADA 6 4 Solução NÃO ADMISSÍVEL 2 0 Produção = 8 un. de P 1 Limite Superior = 6 unidades Folga = 6 -8= -2 unidades 2 4 6 8 10 x 1 Considerando “F 1 ” a variável de folga, a restrição técnica x 1 < 6 transforma-se na equação x 1 + F 1 = 6 com F 1 > 0 20
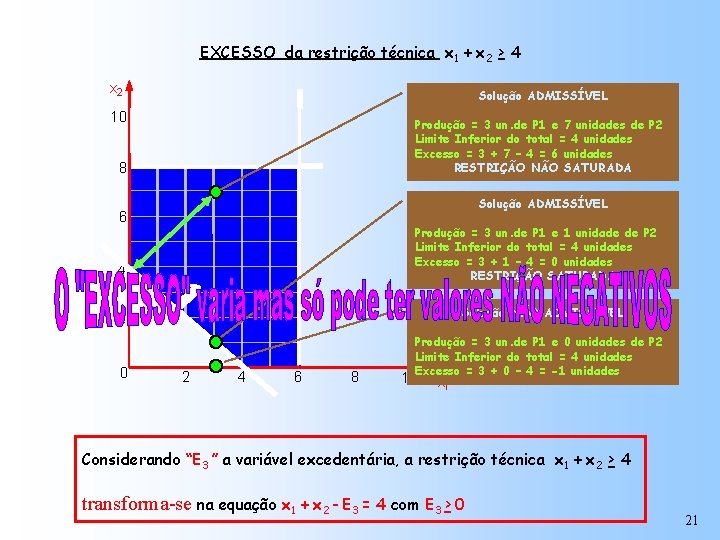
EXCESSO da restrição técnica x 1 + x 2 > 4 x 2 Solução ADMISSÍVEL 10 Produção = 3 un. de P 1 e 7 unidades de P 2 Limite Inferior do total = 4 unidades Excesso = 3 + 7 – 4 = 6 unidades RESTRIÇÃO NÃO SATURADA 8 Solução ADMISSÍVEL 6 Produção = 3 un. de P 1 e 1 unidade de P 2 Limite Inferior do total = 4 unidades Excesso = 3 + 1 – 4 = 0 unidades RESTRIÇÃO SATURADA 4 Solução NÃO ADMISSÍVEL 2 0 2 4 6 8 Produção = 3 un. de P 1 e 0 unidades de P 2 Limite Inferior do total = 4 unidades Excesso = 3 + 0 – 4 = -1 unidades 10 x 1 Considerando “E 3 ” a variável excedentária, a restrição técnica x 1 + x 2 > 4 transforma-se na equação x 1 + x 2 - E 3 = 4 com E 3 > 0 21

AS VARIÁVEIS AUXILIARES PERMITEM “EQUILIBRAR” AS RESTRIÇÕES DE UM MODELO Max f(X)=3 x 1 + 5 x 2 (lucro a maximizar) sujeito a: x 1 < 6 (produção de P 1 não deve exceder 6 unidades) x 2 < 8 (produção de P 2 não deve exceder 8 unidades) x 1 + x 2 > 4 (produção total mínima de 4 unidades) x 1 , x 2 > 0 (não negatividade) 22

AS VARIÁVEIS AUXILIARES PERMITEM “EQUILIBRAR” AS RESTRIÇÕES DE UM MODELO Max f(X)=3 x 1 + 5 x 2 + 0 F 1 sujeito a: x 1 + F 1 = 6 (restrição do tipo < equilibra com variável de FOLGA) x 2 < 8 (produção de P 2 não deve exceder 8 unidades) x 1 + x 2 > 4 (produção total mínima de 4 unidades) x 1 , x 2 , F 1 > 0 (não negatividade) 23

AS VARIÁVEIS AUXILIARES PERMITEM “EQUILIBRAR” AS RESTRIÇÕES DE UM MODELO Max f(X)=3 x 1 + 5 x 2 + 0 F 1 + 0 F 2 sujeito a: x 1 + F 1 = 6 (restrição do tipo < equilibra com variável de FOLGA) x 2 + F 2 = 8 x 1 + x 2 > 4 (restrição do tipo < equilibra com variável de FOLGA) (produção total mínima de 4 unidades) x 1 , x 2 , F 1 , F 2 > 0 (não negatividade) 24

AS VARIÁVEIS DE FOLGA E EXCEDENTÁRIAS PERMITEM “EQUILIBRAR” TODAS AS RESTRIÇÕES DO MODELO Max f(X)=3 x 1 + 5 x 2 + 0 F 1 + 0 F 2 + 0 E 3 sujeito a: x 1 + F 1 = 6 (restrição do tipo < equilibra com variável de FOLGA) x 2 + F 2 = 8 (restrição do tipo x 1 + x 2 – E 3 = 4 < equilibra com variável de FOLGA) (restrição do tipo > equilibra com variável EXCEDENTÁRIA) x 1 , x 2 , F 1 , F 2 , E 3 > 0 (não negatividade) 25

AS VARIÁVEIS DE FOLGA E EXCEDENTÁRIAS PERMITEM “EQUILIBRAR” TODAS AS RESTRIÇÕES DO MODELO Max f(X)=3 x 1 + 5 x 2 + 0 F 1 + 0 F 2 + 0 E 3 sujeito a: x 1 + F 1 = 6 x 2 + F 2 = 8 Sistema de Equações para cálculo da solução óptima x 1 + x 2 – E 3 = 4 x 1 , x 2 , F 1 , F 2 , E 3 > 0 (não negatividade) 26

(ligue o som) 27

28

29

PROGRAMAÇÃO MATEMÁTICA l l Técnica utilizada para calcular a solução óptima de um problema que requer uma decisão ou um conjunto de decisões acerca do melhor uso de um conjunto limitado de recursos disponíveis para atingir um ou mais objectivos “Passos” a executar – Conversão do problema proposto num modelo matemático que incorpore os elementos essenciais do problema. – Exploração das diferentes soluções do problema. – Calcular a solução mais favorável ou a solução óptima. l A Programação Matemática Linear (PL) requer que, no modelo, todas as funções sejam lineares. 30

PL - Terminologia l l l l l Solução (decisão, ponto): conjunto de valores para todas as variáveis do modelo (decisão e auxiliares) independentemente de serem desejáveis ou mesmo admissíveis Solução admissível: uma solução que satisfaz todas as restrições (técnicas e lógicas). Região admissível (espaço das soluções admissíveis, convexo das soluções admissíveis): colecção de todas as soluções admissíveis Rectas de nível da função objectivo (linhas de isocusto ou isolucro): rectas em cujos pontos a função tem o mesmo valor Solução Óptima (óptimo): uma solução admissível onde a função atinge o valor mais favorável (máximo ou mínimo) Valor Óptimo: valor da função objectivo associado a uma solução óptima. Restrição activa: diz-se de uma restrição saturada (a variável auxiliar é nula) Restrição inactiva ou não activa: diz-se de uma restrição não saturada (variável auxiliar não nula) Restrição redundante: é uma restrição que resulta da combinação linear de outras restrições do modelo Ponto extremo: é um ponto do conjunto de soluções que não pode ser obtido por combinação linear convexa de pontos do conjunto 31
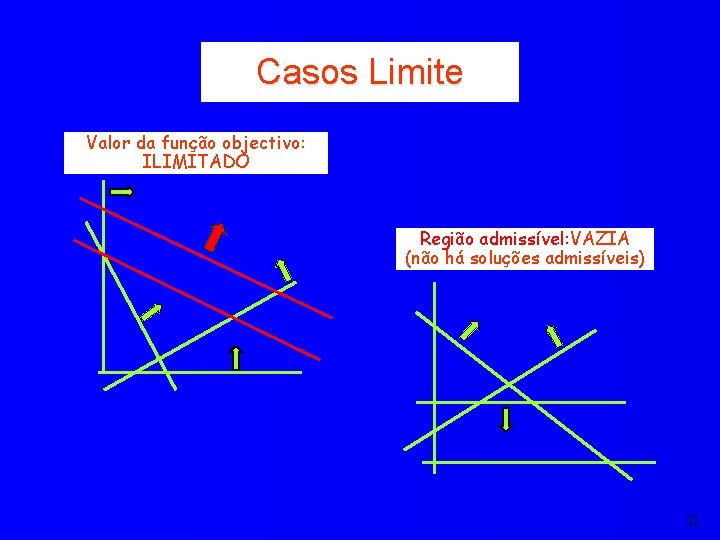
Casos Limite Valor da função objectivo: ILIMITADO Região admissível: VAZIA (não há soluções admissíveis) 32

Teoria da Programação Linear Um problema de PL pode ser de um dos três tipos seguintes: l l l Sem solução: a região admissível é vazia Solução ilimitada : a região admissível é ilimitada na direcção óptima de optimização Solução admissível e limitada : há região admissível e num ou mais dos seus extremos a solução é óptima. Nesta ou nestas soluções pode haver: - óptimo único (solução óptima única) - mais do que um óptimo: solução óptima múltipla ou indeterminada 33

34
- Slides: 34