Modelling induction heating of ionic solutions using COMSOL

Modelling induction heating of ionic solutions using COMSOL Dr M J Taylor CPhy FInst. P Perpetual Research Consultancy Ltd

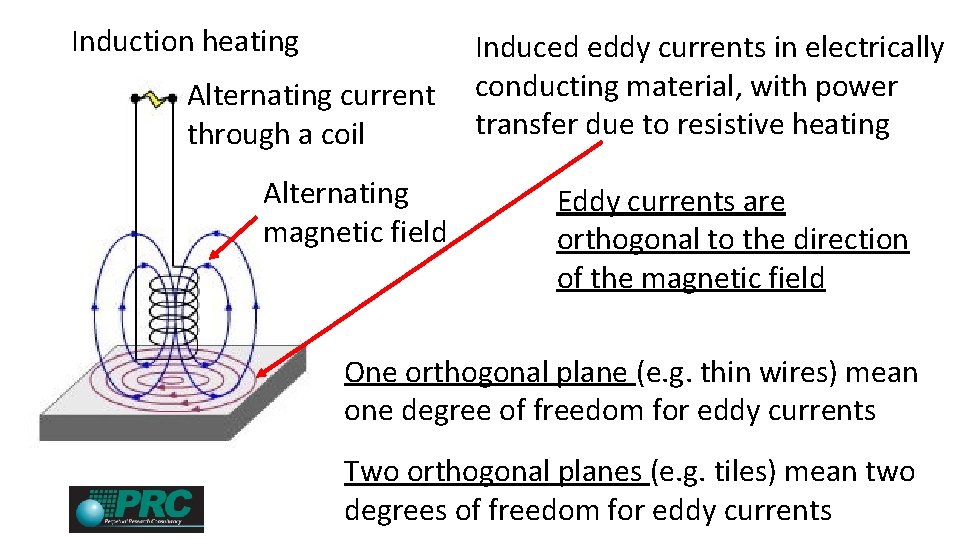
Induction heating Induced eddy currents in electrically Alternating current conducting material, with power transfer due to resistive heating through a coil Alternating magnetic field Eddy currents are orthogonal to the direction of the magnetic field One orthogonal plane (e. g. thin wires) mean one degree of freedom for eddy currents Two orthogonal planes (e. g. tiles) mean two degrees of freedom for eddy currents

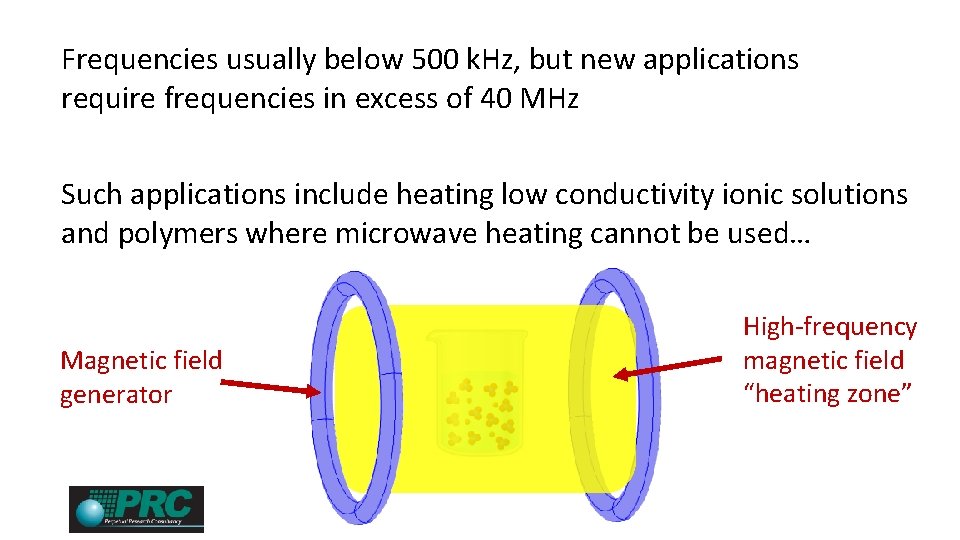
Frequencies usually below 500 k. Hz, but new applications require frequencies in excess of 40 MHz Such applications include heating low conductivity ionic solutions and polymers where microwave heating cannot be used… Magnetic field generator High-frequency magnetic field “heating zone”

The specific power transferred via induction heating can be described by a numerical approximation: Equ (1)

Experimental validation is difficult at megahertz frequencies Equ (1) So the AC/DC model of COMSOL has been used in a 3 D frequency-transient study The aim of this study was to validate the equation, and determine the value of k for different geometries, for frequencies from 2 MHz to 40 MHz

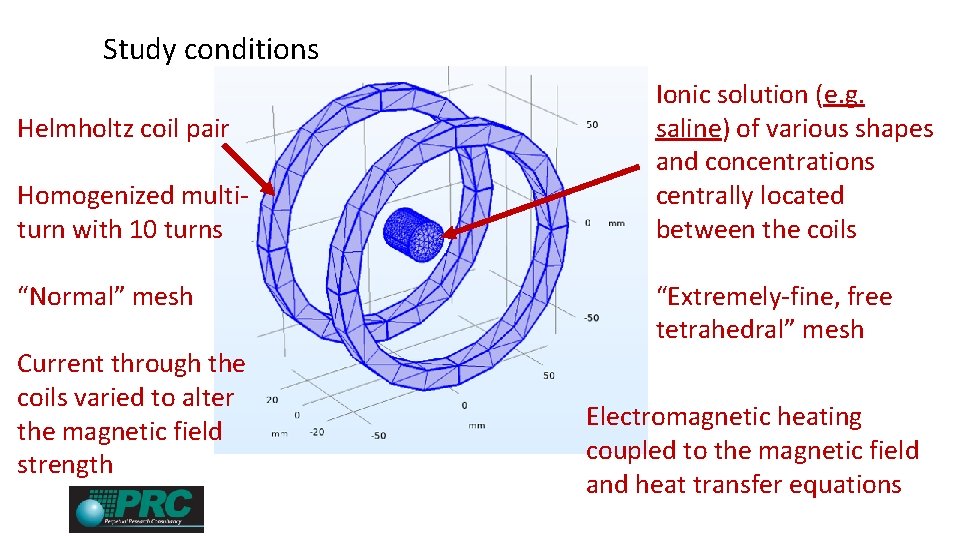
Study conditions Helmholtz coil pair Homogenized multiturn with 10 turns “Normal” mesh Current through the coils varied to alter the magnetic field strength Ionic solution (e. g. saline) of various shapes and concentrations centrally located between the coils “Extremely-fine, free tetrahedral” mesh Electromagnetic heating coupled to the magnetic field and heat transfer equations

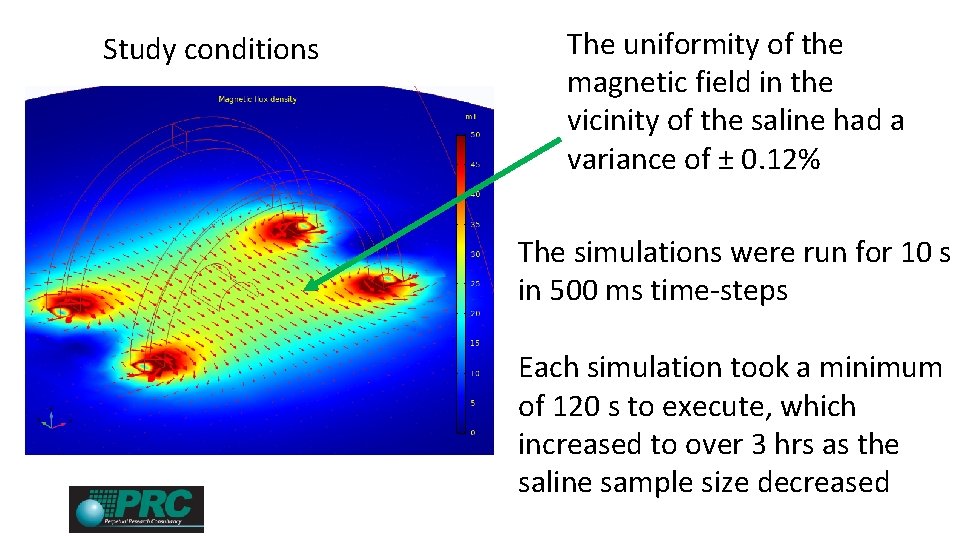
Study conditions The uniformity of the magnetic field in the vicinity of the saline had a variance of ± 0. 12% The simulations were run for 10 s in 500 ms time-steps Each simulation took a minimum of 120 s to execute, which increased to over 3 hrs as the saline sample size decreased

Equ (1) can be re-arranged to give the heating rate of an inductively heated body Equ (2)

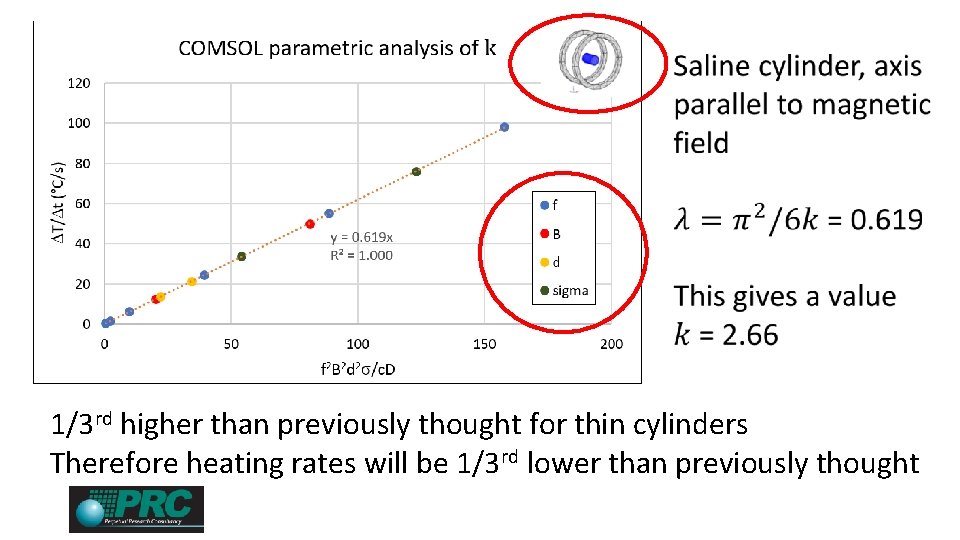
1/3 rd higher than previously thought for thin cylinders Therefore heating rates will be 1/3 rd lower than previously thought

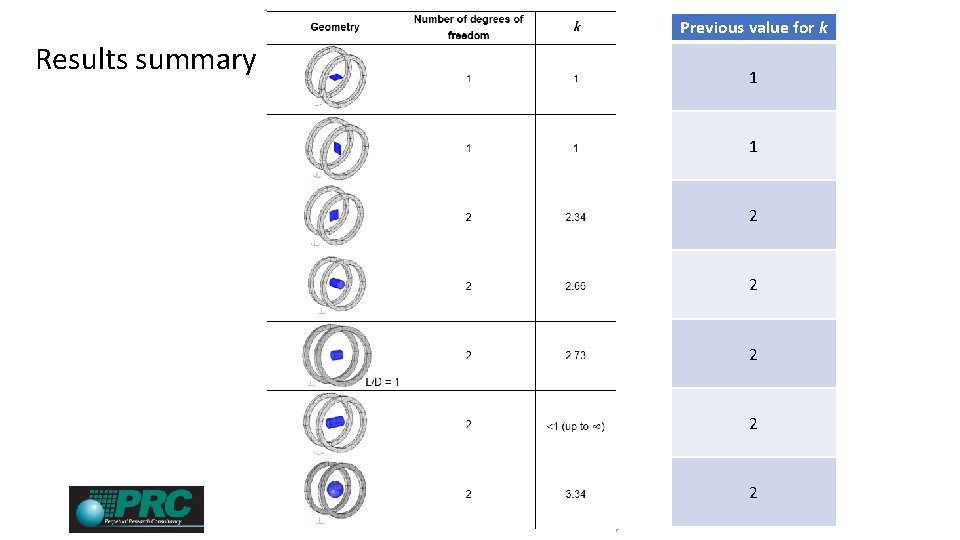
Results summary Previous value for k 1 1 2 2 2

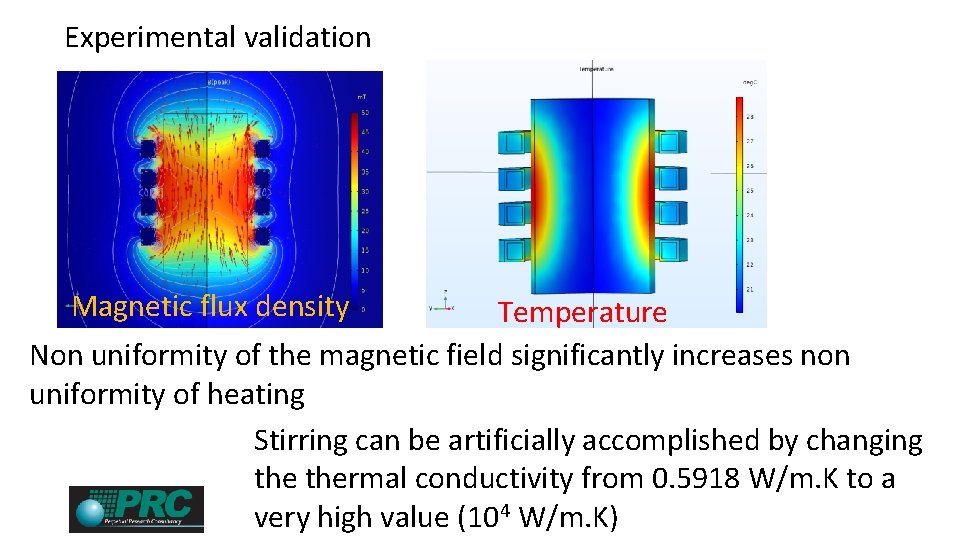
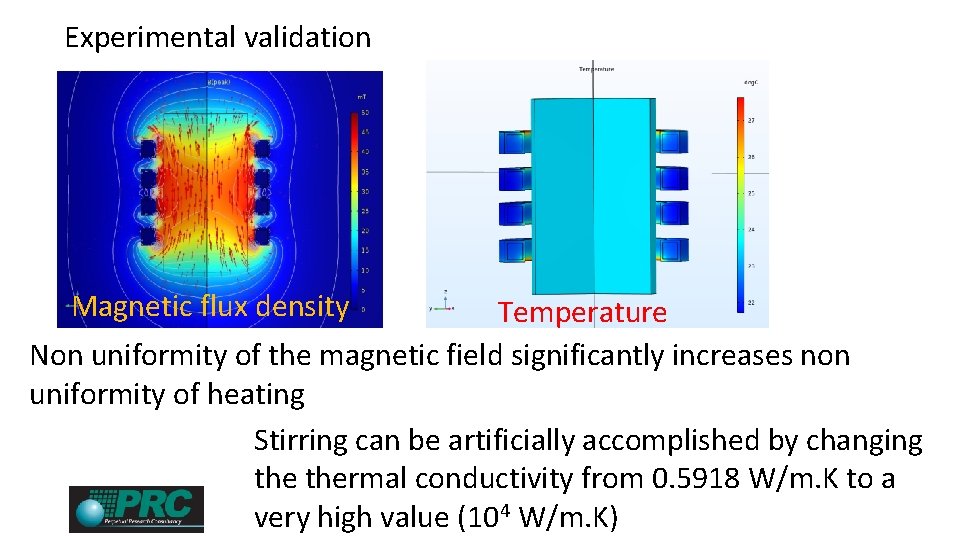
Experimental validation Inductive heating tests at 2 MHz undertaken courtesy of Trumpf Hüttinger Gmb. H, Freiburg

Experimental validation Inductive heating tests at 2 MHz undertaken courtesy of Trumpf Hüttinger Gmb. H, Freiburg

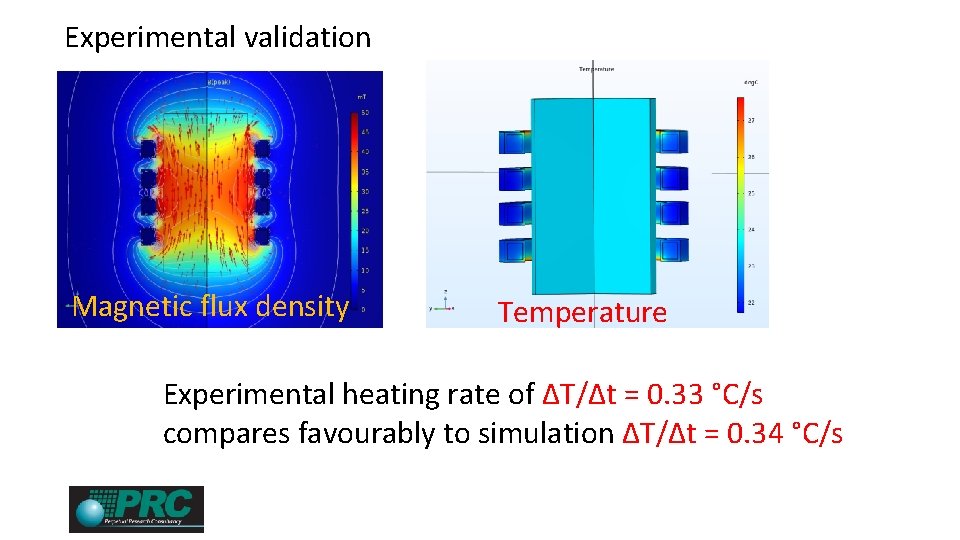
Experimental validation Magnetic flux density Temperature Non uniformity of the magnetic field significantly increases non uniformity of heating Stirring can be artificially accomplished by changing thermal conductivity from 0. 5918 W/m. K to a very high value (104 W/m. K)

Experimental validation Magnetic flux density Temperature Non uniformity of the magnetic field significantly increases non uniformity of heating Stirring can be artificially accomplished by changing thermal conductivity from 0. 5918 W/m. K to a very high value (104 W/m. K)

Experimental validation Magnetic flux density Temperature Experimental heating rate of ΔT/Δt = 0. 33 °C/s compares favourably to simulation ΔT/Δt = 0. 34 °C/s

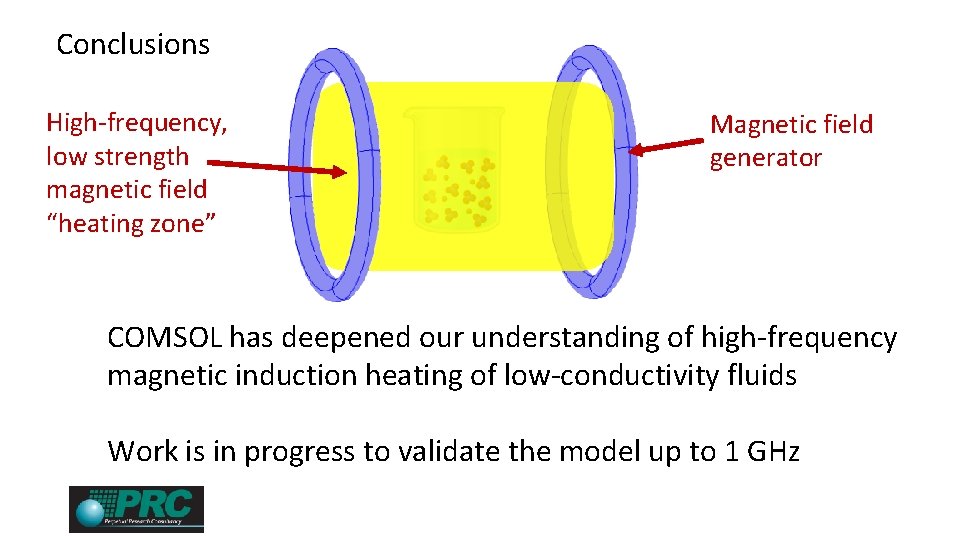
Conclusions High-frequency, low strength magnetic field “heating zone” Magnetic field generator COMSOL has deepened our understanding of high-frequency magnetic induction heating of low-conductivity fluids Work is in progress to validate the model up to 1 GHz

Thank you Questions?