Modelling in Mechanics Learning Calculate with SUVAT equations

Modelling in Mechanics Learning Calculate with SUVAT equations Objective 1 2 3 How do you find the velocity from a displacement time graph? 4 How do you find displacement from a velocity time graph? 5 Oasis Academy South Bank 6 th Form

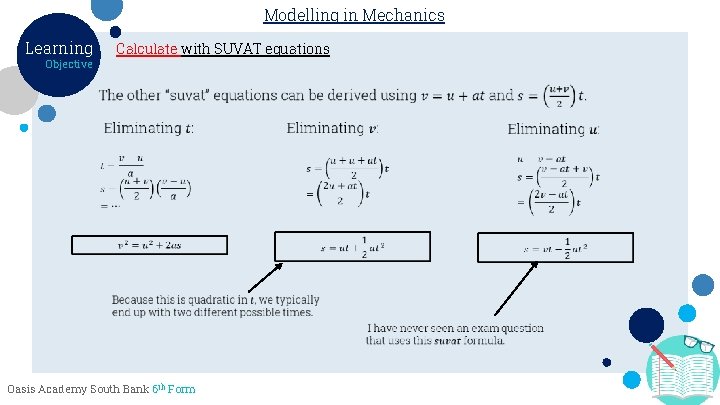
Modelling in Mechanics Learning Calculate with SUVAT equations Objective When there is constant acceleration, there a variety of formulae which relate the following 5 quantities: Velocity Oasis Academy South Bank 6 th Form Time

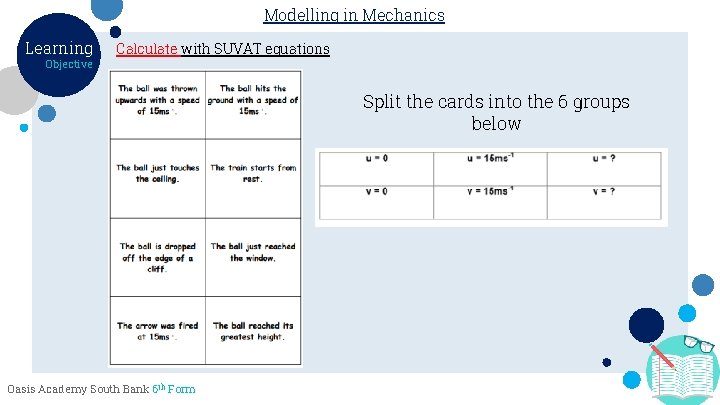
Modelling in Mechanics Learning Objective Calculate with SUVAT equations Split the cards into the 6 groups below Oasis Academy South Bank 6 th Form

Modelling in Mechanics Learning Calculate with SUVAT equations Objective A cyclist is travelling along a straight road. She accelerates at a constant rate from a velocity of 4 ms-1 to a velocity of 7. 5 ms-1 in 40 seconds. Find: (a) the distance she travels in these 40 seconds (b) her acceleration in these 40 seconds. Oasis Academy South Bank 6 th Form Always write each letter of suvat, putting a “? ” for any quantities you need to find.

Modelling in Mechanics Learning Objective Calculate with SUVAT equations Oasis Academy South Bank 6 th Form

Modelling in Mechanics Learning Calculate with SUVAT equations Objective [Textbook] A car moves from traffic lights along a straight road with constant acceleration. The car starts from rest at the traffic lights and 30 second later the car passes a speed-trap where it is registered as travelling at 45 km h-1. Find: (a) the acceleration of the car (b) the distance between the traffic lights and the speed-trap. Ensure everything is in SI units first. Oasis Academy South Bank 6 th Form

Modelling in Mechanics Learning Objective Calculate with SUVAT equations Oasis Academy South Bank 6 th Form

Modelling in Mechanics Learning Calculate with SUVAT equations Objective Oasis Academy South Bank 6 th Form

Modelling in Mechanics Learning Calculate with SUVAT equations Objective Oasis Academy South Bank 6 th Form

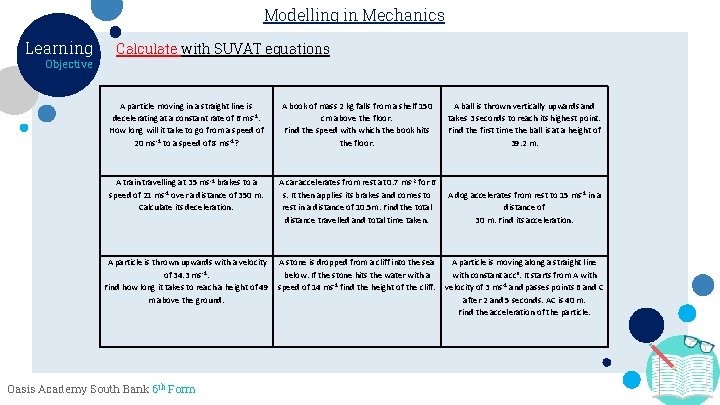
Modelling in Mechanics Learning Objective Calculate with SUVAT equations A particle moving in a straight line is decelerating at a constant rate of 6 ms-1. How long will it take to go from a speed of 20 ms-1 to a speed of 8 ms-1? A book of mass 2 kg falls from a shelf 150 cm above the floor. Find the speed with which the book hits the floor. A ball is thrown vertically upwards and takes 3 seconds to reach its highest point. Find the first time the ball is at a height of 39. 2 m. A train travelling at 35 ms-1 brakes to a speed of 21 ms-1 over a distance of 350 m. Calculate its deceleration. A car accelerates from rest at 0. 7 ms-2 for 6 s. It then applies its brakes and comes to rest in a distance of 10. 5 m. Find the total distance travelled and total time taken. A dog accelerates from rest to 15 ms-1 in a distance of 30 m. Find its acceleration. A particle is thrown upwards with a velocity A stone is dropped from a cliff into the sea A particle is moving along a straight line of 34. 3 ms-1. below. If the stone hits the water with a with constant accn. It starts from A with -1 Find how long it takes to reach a height of 49 speed of 14 ms find the height of the cliff. velocity of 3 ms-1 and passes points B and C m above the ground. after 2 and 5 seconds. AC is 40 m. Find the acceleration of the particle. Oasis Academy South Bank 6 th Form

Modelling in Mechanics Learning Objective Calculate with SUVAT equations Answer the first problem and then rewrite the problem to take into account the change in the variables and requirements for the other boxes on the sheet. You can keep the context of a puck on the ice or you might prefer to change it (particularly for positive acceleration). Oasis Academy South Bank 6 th Form

Modelling in Mechanics Learning Objective Calculate with SUVAT equations Oasis Academy South Bank 6 th Form

13 Groups:

A cyclist is travelling along a straight road. She accelerates at a constant rate from a velocity of 4 ms-1 to a velocity of 7. 5 ms-1 in 40 seconds. Find: (a) the distance she travels in these 40 seconds (b) her acceleration in these 40 seconds. A cyclist is travelling along a straight road. She accelerates at a constant rate from a velocity of 4 ms-1 to a velocity of 7. 5 ms-1 in 40 seconds. Find: (a) the distance she travels in these 40 seconds (b) her acceleration in these 40 seconds.

[Textbook] A car moves from traffic lights along a straight road with constant acceleration. The car starts from rest at the traffic lights and 30 second later the car passes a speed-trap where it is registered as travelling at 45 km h-1. Find: (a) the acceleration of the car (b) the distance between the traffic lights and the speed-trap. [Textbook] A car moves from traffic lights along a straight road with constant acceleration. The car starts from rest at the traffic lights and 30 second later the car passes a speed-trap where it is registered as travelling at 45 km h-1. Find: (a) the acceleration of the car (b) the distance between the traffic lights and the speed-trap.