Modelling Complex Systems Video 4 A simple example

Traditional models • • Probability theory and distributions. Ordinary differential equation models. Difference equations.

Using traditional models Usually a whole course or number of courses will be dedicated

‘Complex systems’ models • Cellular automata • Agent-based models • Self-propelled particles All are

`Complex systems’ models The basic approach is to write down an algorithm which describes

A very simple (not complex) example Lets assume we want to model two connected

Simulation Code %Number of particles N=50; %Simulation of Ehrenfest model %x is number in

Importance of multiple runs R=100; for j=1: R %Initial conditions MAIN CODE HERE %Store

Complex Systems Approach Express a model as an ‘algorithm’ Simulate it lots of times.

Code The code to generate the figures on the previous slides can be found

Slides: 22

Download presentation

Modelling Complex Systems Video 4: A simple example in a complex way

Traditional models • • Probability theory and distributions. Ordinary differential equation models. Difference equations. Partial differential equation models. Stochastic differential equations. Partial differential equations. Markov chain models Statistical mechanics models.

Using traditional models Usually a whole course or number of courses will be dedicated to looking at each technique. Each types of models are also useful in modelling complex systems. But we do not take any particular traditional model as our starting point. Instead we switch backwards and forwards between different approaches.

‘Complex systems’ models • Cellular automata • Agent-based models • Self-propelled particles All are computer simulations.

`Complex systems’ models The basic approach is to write down an algorithm which describes how our complex system works and use this algorithm to better understand the system. This algorithm becomes a computer simulation which we run to see how the system behaves. But the algorithm can also be related to more 'traditional' mathematical models in order that we can better analyse the system.

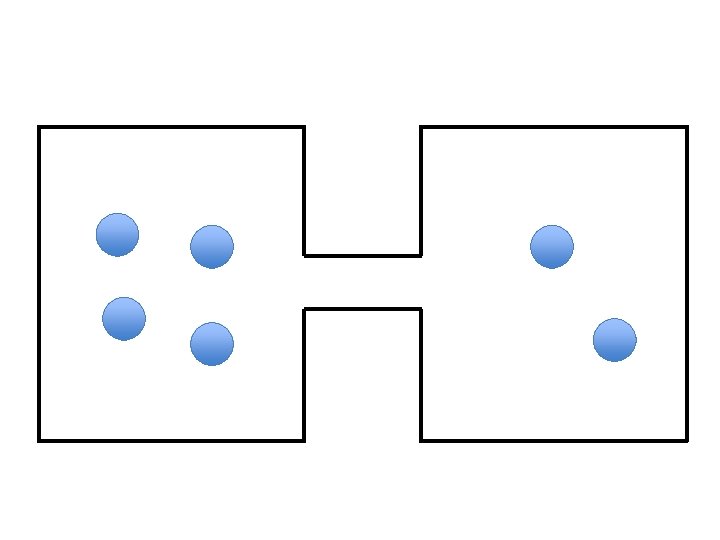
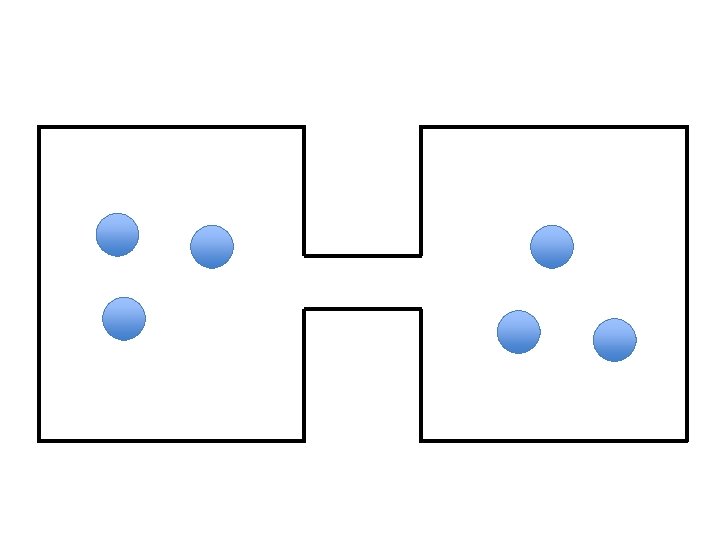
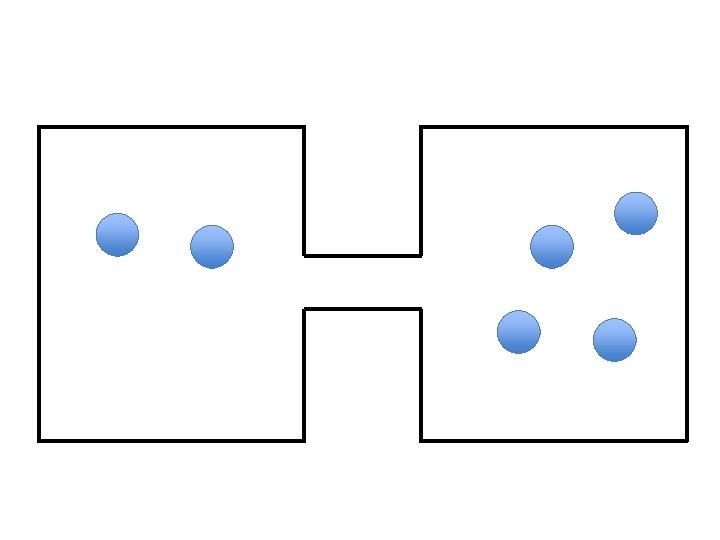
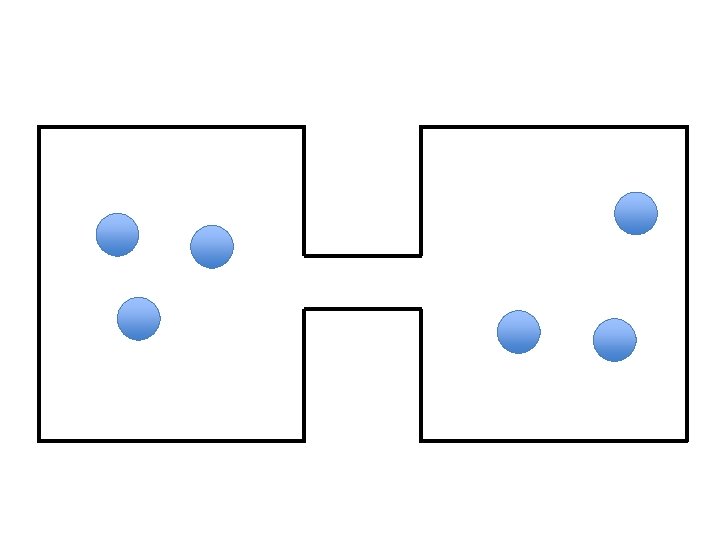
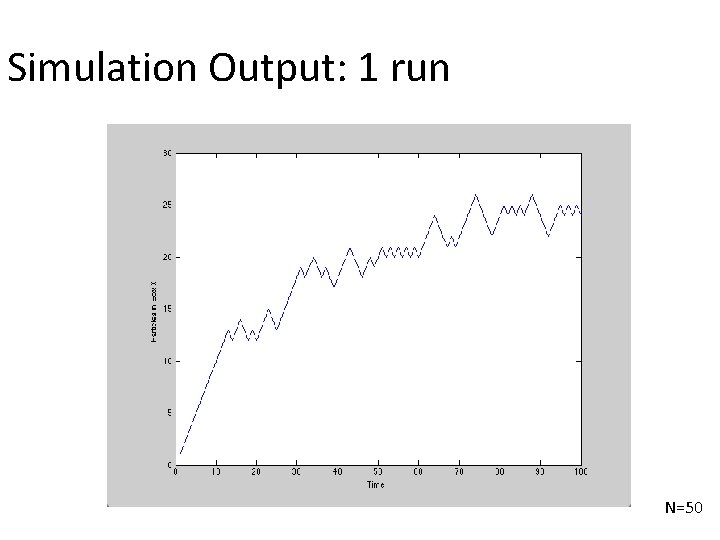
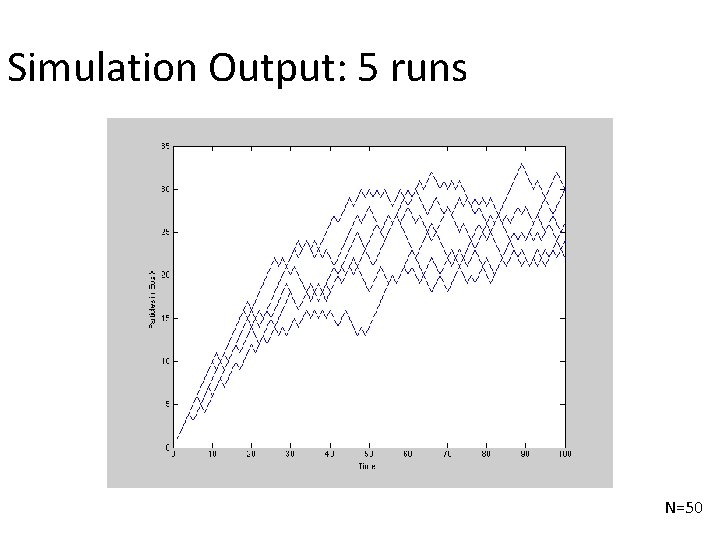
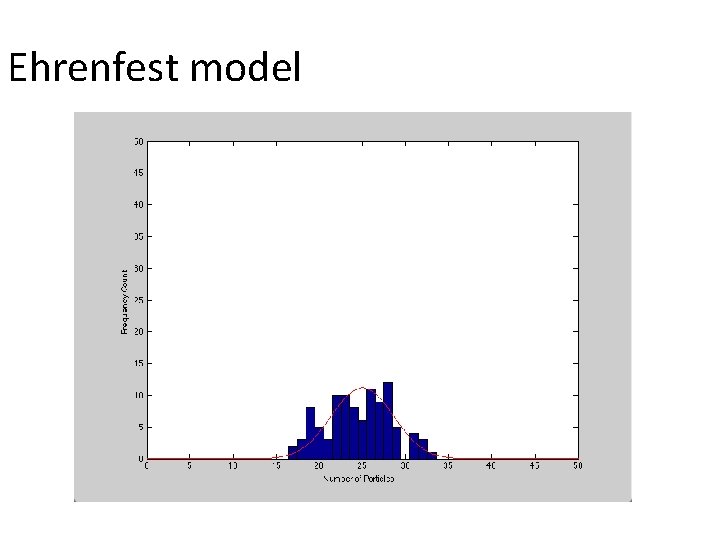
A very simple (not complex) example Lets assume we want to model two connected boxes in which ’particles’ can move • On each time step we choose one particle at random at move it to the other box. • What is the equilibrium distribution of particles between boxes? • How long does it take to reach this equilibrium?

Simulation Code %Number of particles N=50; %Simulation of Ehrenfest model %x is number in box x x(1)=round(rand); for t=1: T-1 if rand<x(t)/N %Leave box x x(t+1)=x(t)-1; else %Enter box x x(t+1)=x(t)+1; end

Simulation Output: 1 run N=50

Simulation Output: 5 runs N=50

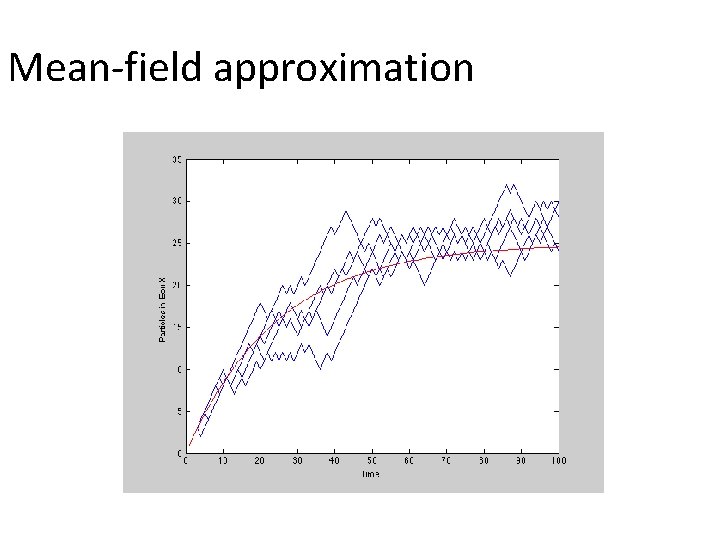
Mean-field approximation

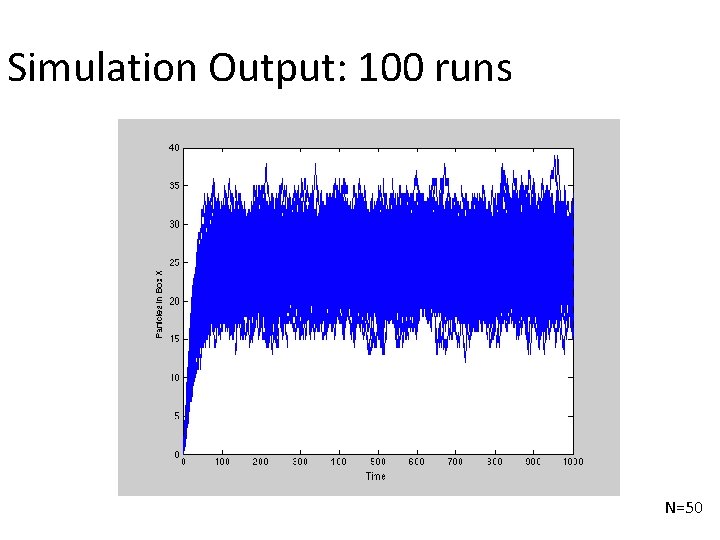
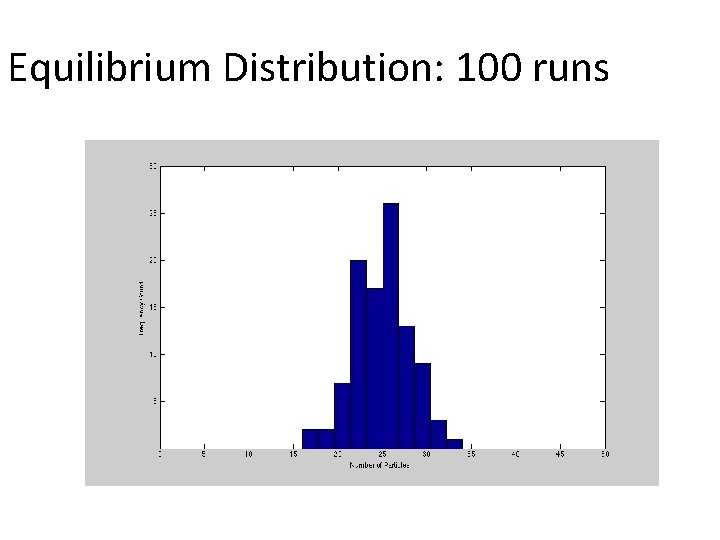
Importance of multiple runs R=100; for j=1: R %Initial conditions MAIN CODE HERE %Store final value xr(j)=x(end); end figure(2) hist(xr, [0: 1: 50]) ylabel('Frequency Count') xlabel('Number of Particles')

Simulation Output: 100 runs N=50

Equilibrium Distribution: 100 runs

Ehrenfest model

Complex Systems Approach Express a model as an ‘algorithm’ Simulate it lots of times. Look at equilibrium distribution. See if we can use traditional mathematics to approximate it. • Compare approximation and simulation. • Systematically investigate the effect of changing a parameter (next lecture). • •

Code The code to generate the figures on the previous slides can be found on studentportalen. Ehrenfest. m