Modelling and simulation of highspeed dynamic wetting phenomena

Modelling and simulation of highspeed dynamic wetting phenomena J. E. Sprittles Y. D. Shikhmurzaev (University of Oxford, U. K. ) (University of Birmingham, U. K. ) Mathematics of Splashing Workshop, ICMS, Edinburgh May 2013

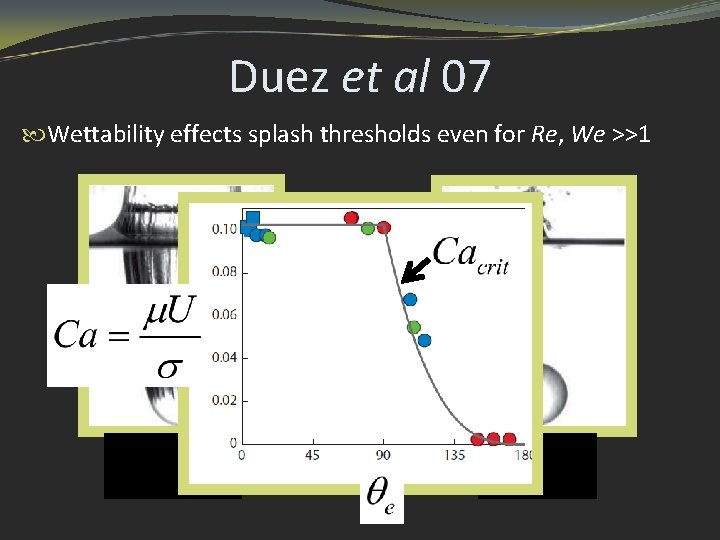
Duez et al 07 Wettability effects splash thresholds even for Re, We >>1

Rein & Delplanque 08 Splash threshold for drop impact can be expressed in terms of the capillary number.

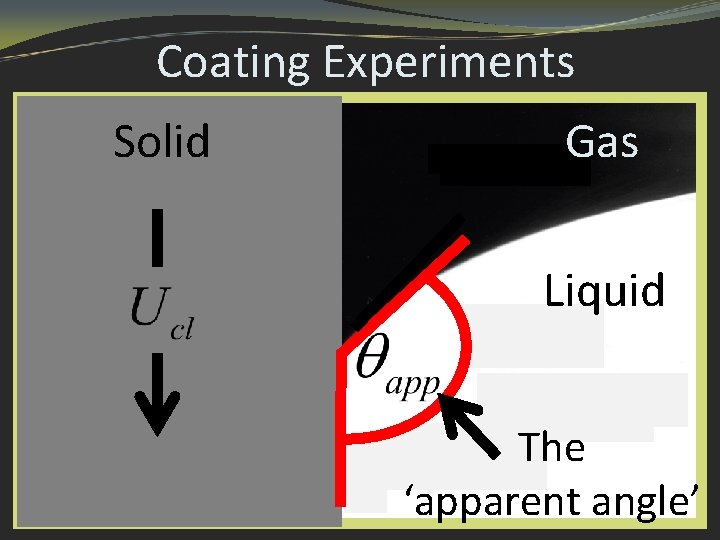
Coating Experiments Solid Advantages: Flow is steady making experimental analysis more tractable. Parameter space is easier to map: Speeds over 6 orders Viscosities over 3 orders Gas Liquid The ‘apparent angle’

Coating Results Apparent angle measured at resolution of 20 microns for water-glycerol solutions with μ=1, 100 m. Pas. Increasing μ

Interpretation A: Static Contact Angle You only observe the ‘apparent angle’. The actual one is fixed. Free surface bends below the experiment’s resolution (20μm) The ‘actual angle’

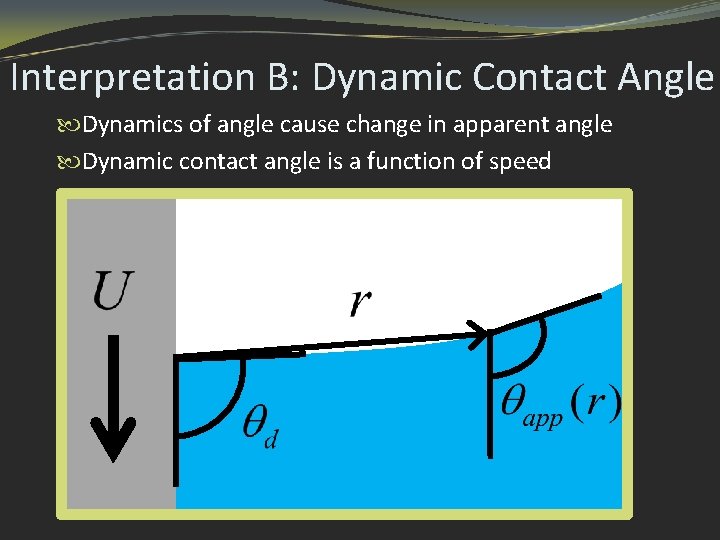
Interpretation B: Dynamic Contact Angle Dynamics of angle cause change in apparent angle Dynamic contact angle is a function of speed

Modelling of Dynamic Wetting Phenomena

The ‘Moving Contact Line Problem’ L. E. Scriven & C. Huh (1971), A. W. Neumann (1971), S. H. Davis (1974), E. B. Dussan (1974), E. Ruckenstein (1974), A. M. Schwartz (1975), M. N. Esmail (1975), L. M. Hocking (1976), O. V. Voinov (1976), C. A. Miller (1976), P. Neogi (1976), S. G. Mason (1977), H. P. Greenspan (1978), F. Y. Kafka (1979), L. Tanner (1979), J. Lowndes (1980), D. J. Benney (1980), W. J. Timson (1980), C. G. Ngan (1982), G. F. Telezke (1982), L. M. Pismen (1982), A. Nir (1982), V. V. Pukhnachev (1982), V. A. Solonnikov (1982), P. -G. de Gennes (1983), V. M. Starov (1983), P. Bach (1985), O. Hassager (1985), K. M. Jansons (1985), R. G. Cox (1986), R. Léger (1986), D. Kröner (1987), J. -F. Joanny (1987), J. N. Tilton (1988), P. A. Durbin (1989), C. Baiocchi (1990), P. Sheng (1990), M. Zhou (1990), W. Boender (1991), A. K. Chesters (1991), A. J. J. van der Zanden (1991), P. J. Haley (1991), M. J. Miksis (1991), D. Li (1991), J. C. Slattery (1991), G. M. Homsy (1991), P. Ehrhard (1991), Y. D. Shikhmurzaev (1991), F. Brochard-Wyart (1992), M. P. Brenner (1993), A. Bertozzi (1993), D. Anderson (1993), R. A. Hayes (1993), L. W. Schwartz (1994), H. -C. Chang (1994), J. R. A. Pearson (1995), M. K. Smith (1995), R. J. Braun (1995), D. Finlow (1996), A. Bose (1996), S. G. Bankoff (1996), I. B. Bazhlekov (1996), P. Seppecher (1996), E. Ram é (1997), R. Chebbi (1997), R. Schunk (1999), N. G. Hadjconstantinou (1999), H. Gouin (10999), Y. Pomeau (1999), P. Bourgin (1999), M. C. T. Wilson (2000), D. Jacqmin (2000), J. A. Diez (2001), M. &Y. Renardy (2001), L. Kondic (2001), L. W. Fan (2001), Y. X. Gao (2001), R. Golestanian (2001), E. Raphael (2001), A. O’Rear (2002), K. B. Glasner (2003), X. D. Wang (2003), J. Eggers (2004), V. S. Ajaev (2005), C. A. Phan (2005), P. D. M. Spelt (2005), J. Monnier (2006)

A) Slip Models (‘The Hydrodynamic Model’)

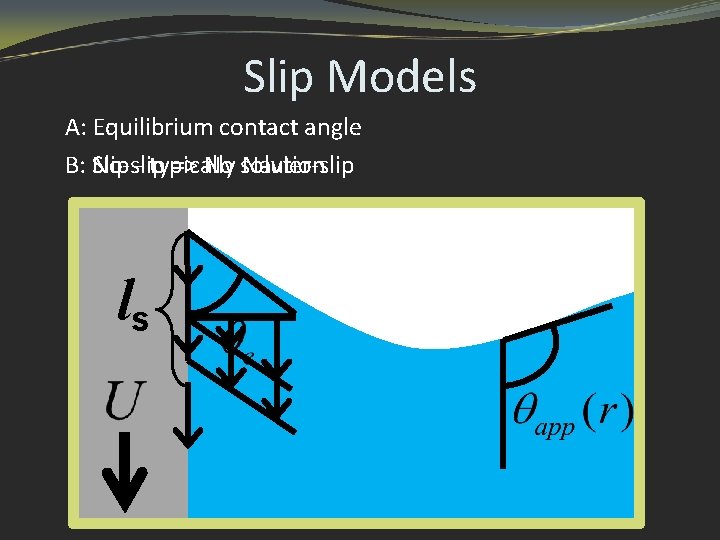
Slip Models A: Equilibrium contact angle B: No-slip Slip - typically => No solution Navier-slip ls

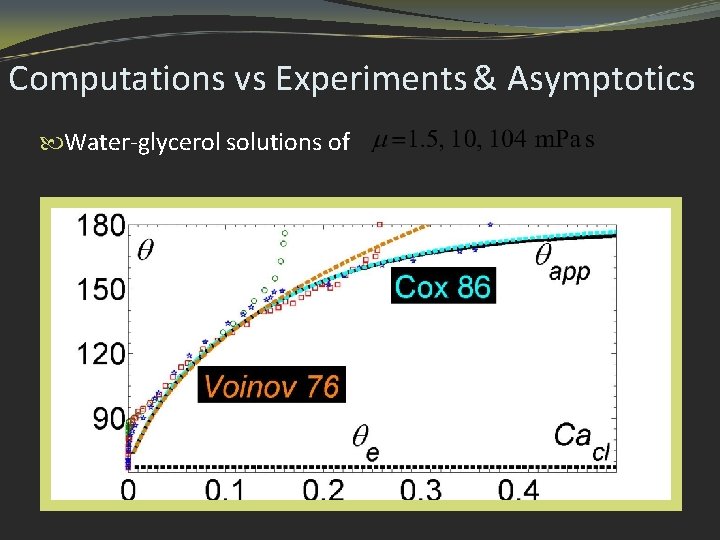
Asymptotics for the Apparent Angle Often, we have In Cox 86, it was shown that in this case: And for Voinov (76) has shown:

A Finite Element Based Computational Framework JES &YDS 2011, Viscous Flows in Domains with Corners, CMAME JES & YDS 2012, Finite Element Framework for Simulating Dynamic Wetting Flows, Int. J. Num. Meth Fluids. JES & YDS, 2012, The Dynamics of Liquid Drops and their Interaction with Surfaces of Varying Wettabilities, Phy. Fluids. JES & YDS, 2013, Finite Element Simulation of Dynamic Wetting Flows as an Interface Formation Process, to J. Comp. Phy.

Mesh Resolution Key

Arbitrary Lagrangian Eulerian Mesh Based on the ‘spine method’ of Scriven and co-workers Microdrop simulation with impact, spreading and rebound

Results: Slip Models

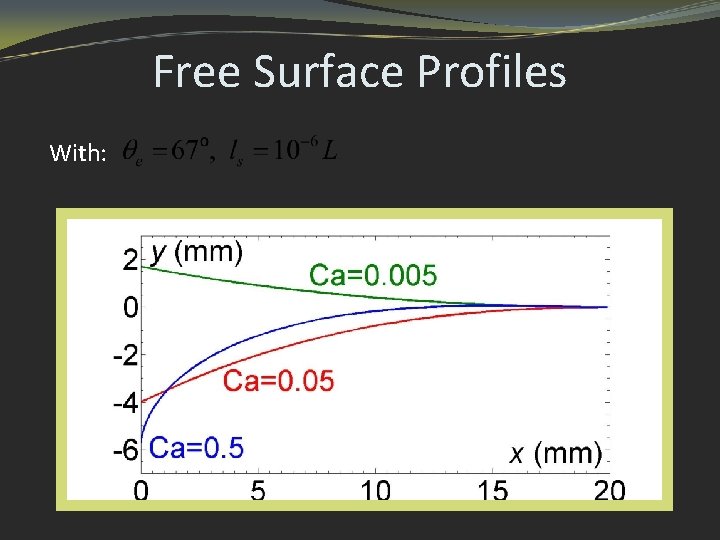
Free Surface Profiles With:

Computations vs Experiments & Asymptotics Water-glycerol solutions of

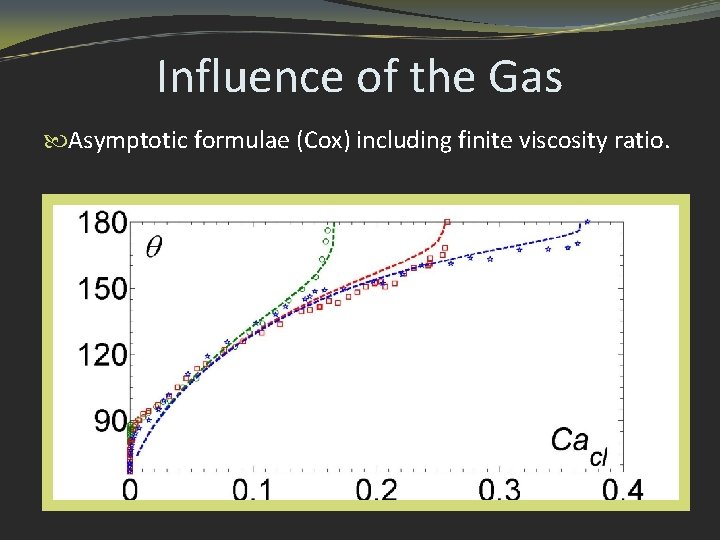
Influence of the Gas Asymptotic formulae (Cox) including finite viscosity ratio.

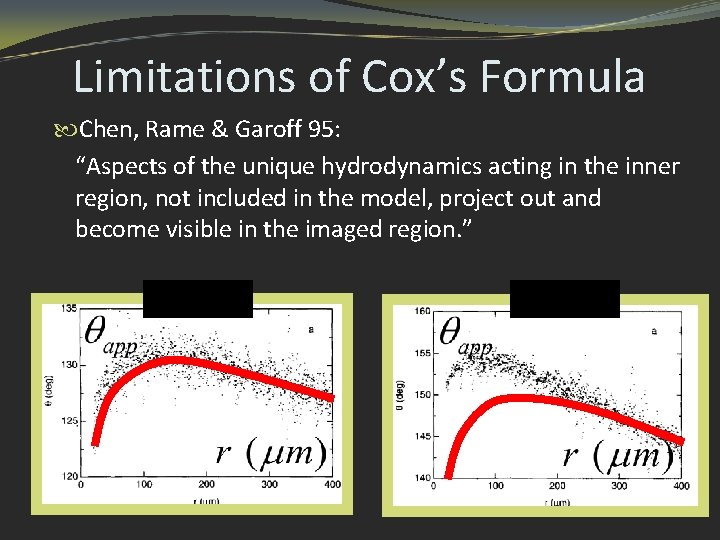
Limitations of Cox’s Formula Chen, Rame & Garoff 95: “Aspects of the unique hydrodynamics acting in the inner region, not included in the model, project out and become visible in the imaged region. ”

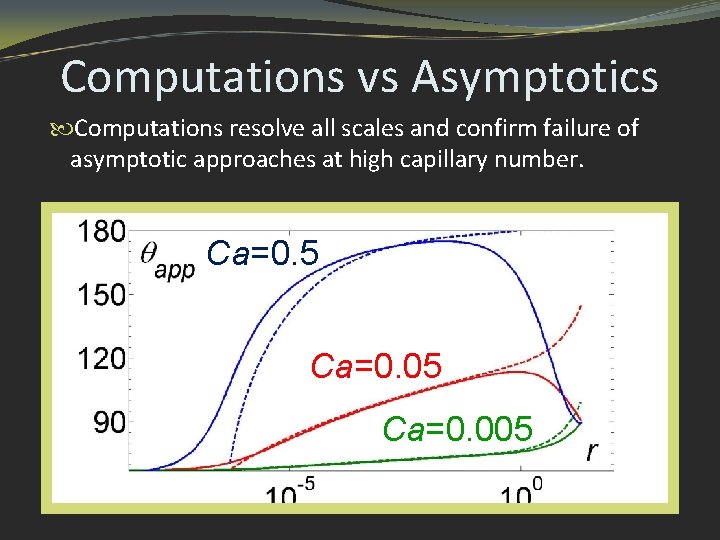
Computations vs Asymptotics Computations resolve all scales and confirm failure of asymptotic approaches at high capillary number. Ca=0. 5 Ca=0. 005

B) Evidence for a Dynamic (Flow Dependent) Angle

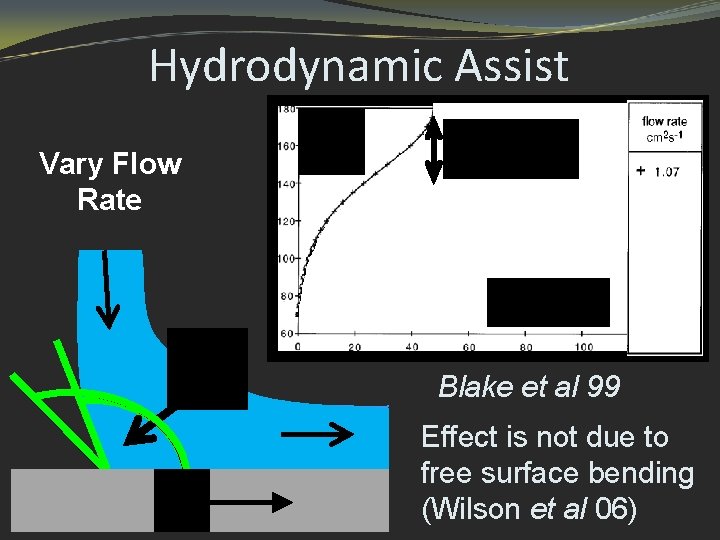
Hydrodynamic Assist Vary Flow Rate U, cm/s Blake et al 99 Effect is not due to free surface bending (Wilson et al 06)

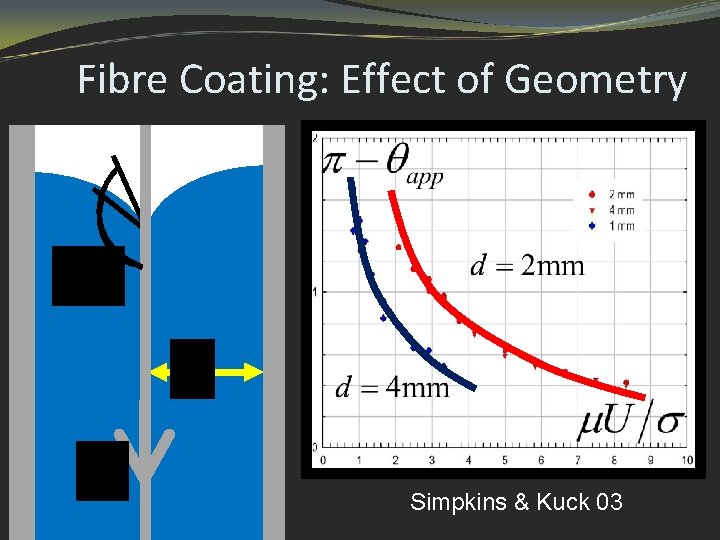
Fibre Coating: Effect of Geometry Simpkins & Kuck 03

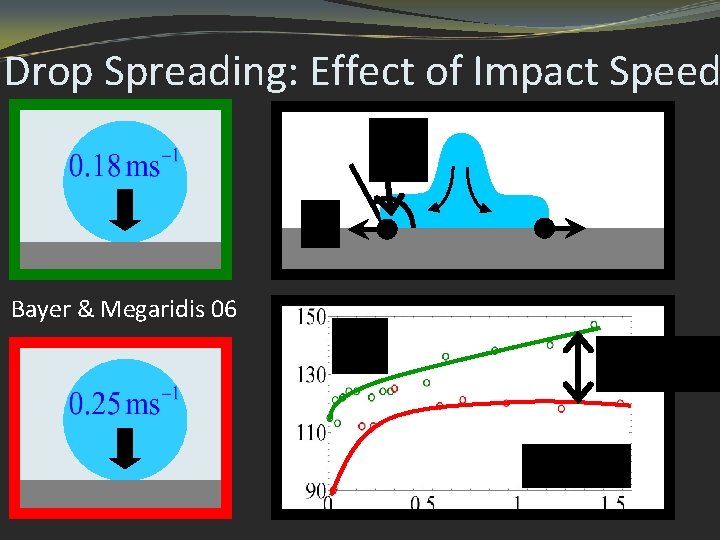
Drop Spreading: Effect of Impact Speed ) Bayer & Megaridis 06

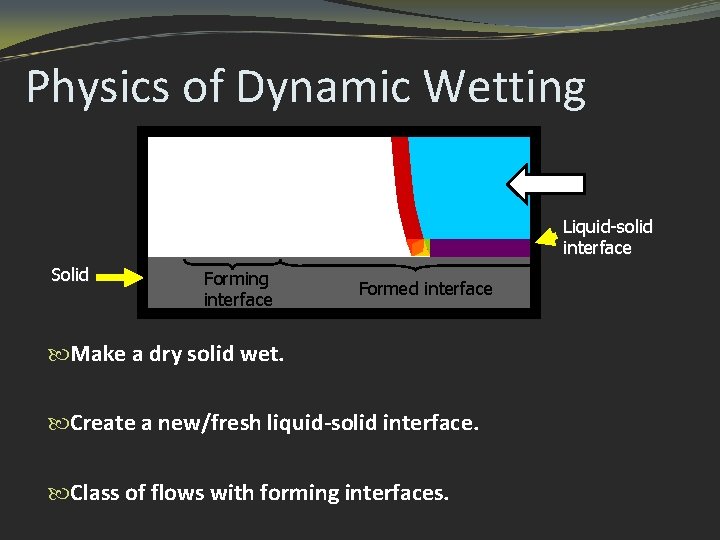
Dynamic Wetting: An Interface Formation Process

Physics of Dynamic Wetting Liquid-solid interface Solid Forming interface Formed interface Make a dry solid wet. Create a new/fresh liquid-solid interface. Class of flows with forming interfaces.

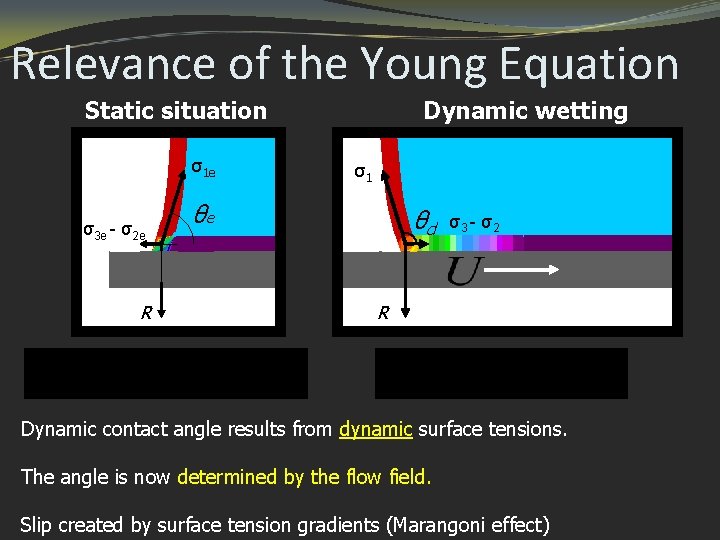
Relevance of the Young Equation Static situation σ1 e σ3 e - σ2 e R Dynamic wetting σ1 θe θd σ3 - σ2 R Dynamic contact angle results from dynamic surface tensions. The angle is now determined by the flow field. Slip created by surface tension gradients (Marangoni effect)

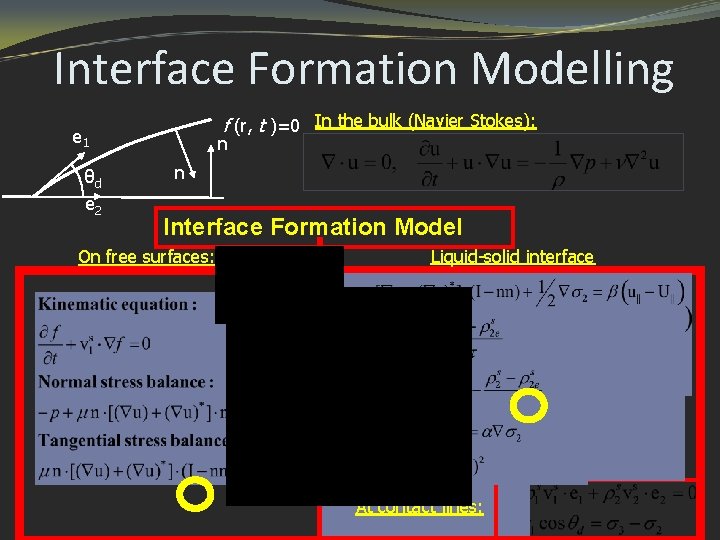
Interface Formation Modelling f (r, t )=0 In the bulk (Navier Stokes): e 1 θd e 2 n n Interface Formation Model On free surfaces: Liquid-solid interface At contact lines:

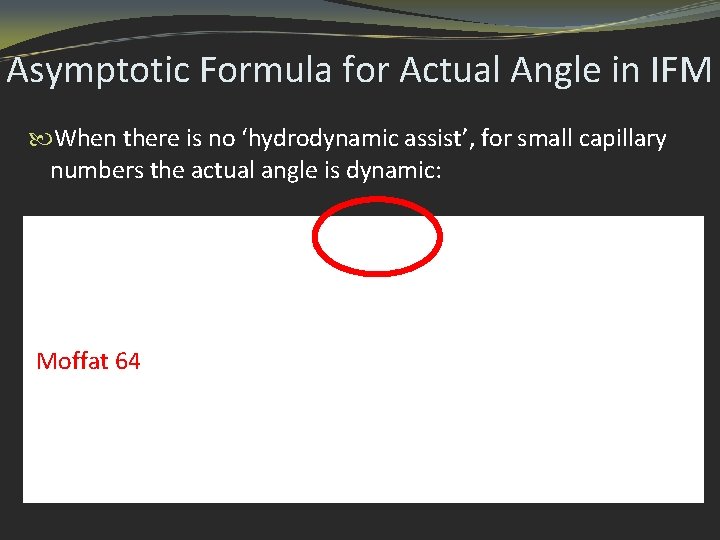
Asymptotic Formula for Actual Angle in IFM When there is no ‘hydrodynamic assist’, for small capillary numbers the actual angle is dynamic: Moffat 64

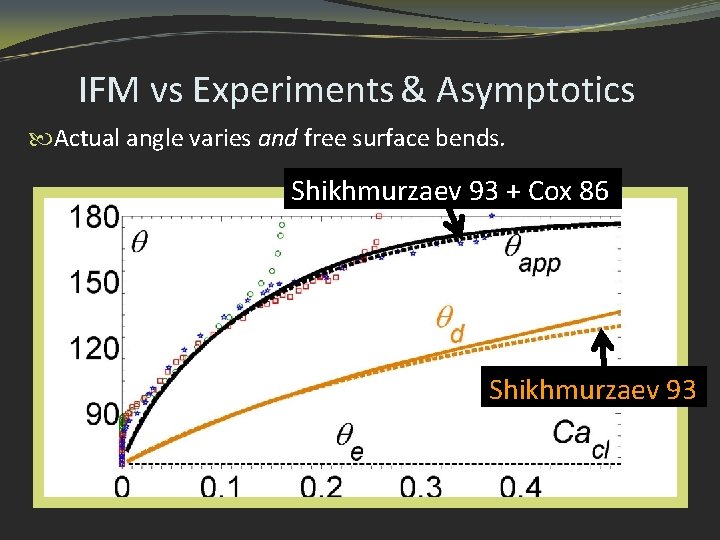
IFM vs Experiments & Asymptotics Actual angle varies and free surface bends. Shikhmurzaev 93 + Cox 86 Shikhmurzaev 93

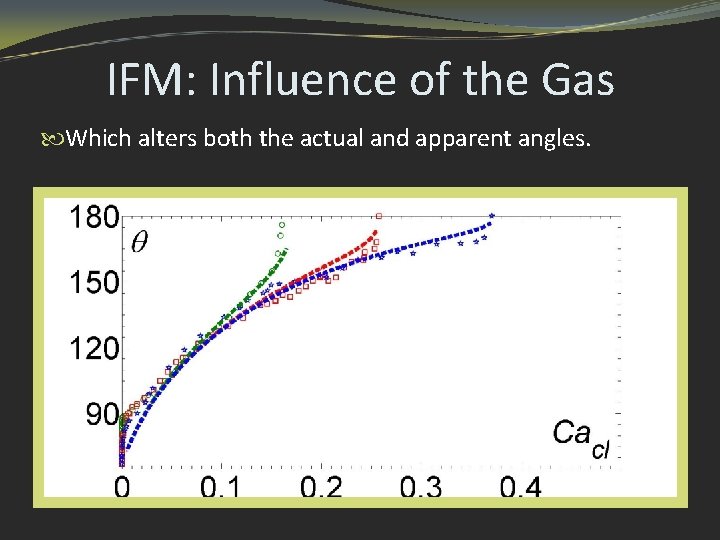
IFM: Influence of the Gas Which alters both the actual and apparent angles.

Microdrop Dynamics

Microdrop Impact ? 25 mm water drop impacting at 5 m/s. Experiments: Dong et al 06

Dynamic Wetting Phenomena 27 mm Radius Tube Millimetre scale Significant Routine 1 Million Orders experimental differences of Magnitude! between measurement models Microfluidics 50 nm Channels Nanofluidics

Coalescence of Liquid Drops: Models vs Experiments

Coalescence of Liquid Drops Developed framework can be adapted for coalescence. Thoroddsen’s Group: Ultra high-speed imaging Nagel’s Group: Sub-optical electrical measurements Experiment Simulation Thoroddsen et al 2005

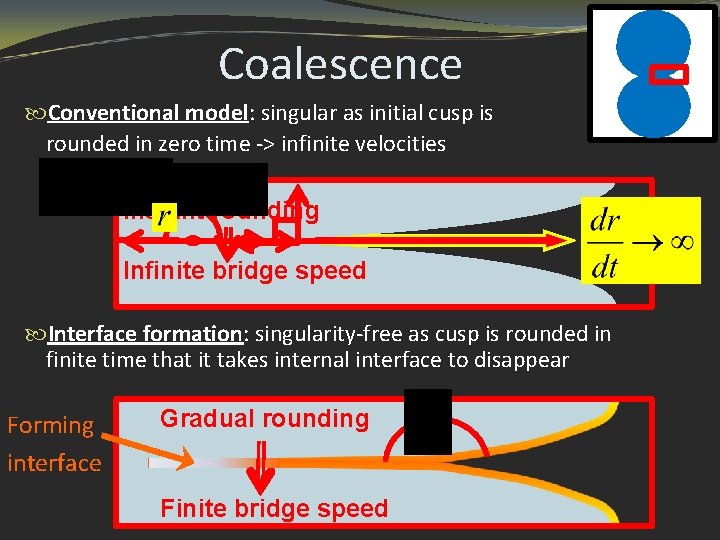
Coalescence Conventional model: singular as initial cusp is rounded in zero time -> infinite velocities Instant rounding Infinite bridge speed Interface formation: singularity-free as cusp is rounded in finite time that it takes internal interface to disappear Forming interface Gradual rounding Finite bridge speed

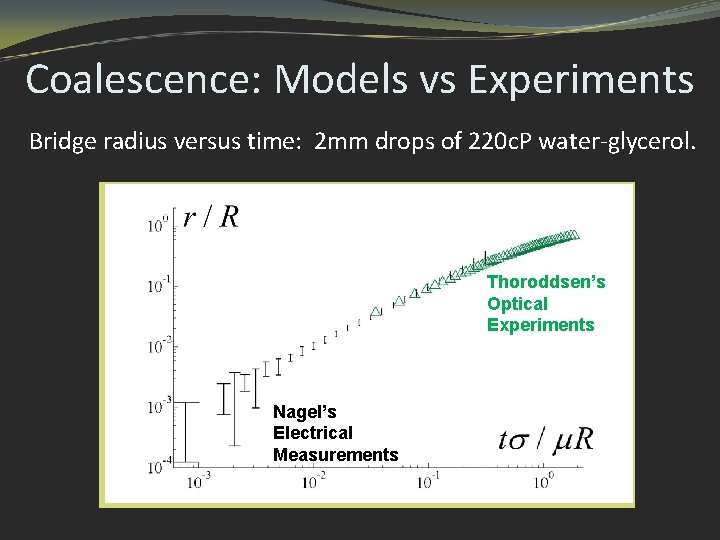
Coalescence: Models vs Experiments Bridge radius versus time: 2 mm drops of 220 c. P water-glycerol. Thoroddsen’s Optical Experiments Conventional Interface formation Nagel’s Electrical Measurements

Microfluidic Dynamic Wetting Phenomena

Microscale Dynamic Wetting Ultra high speed imaging of microfluidic wetting phenomenon, with Dr E. Li & Professor S. T. Thoroddsen

Funding This presentation is based on work supported by:

Thanks

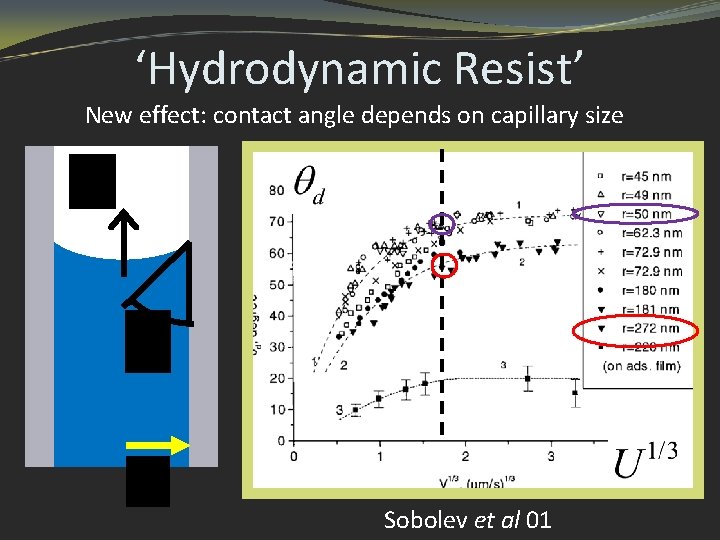
‘Hydrodynamic Resist’ New effect: contact angle depends on capillary size Smaller Capillaries Sobolev et al 01

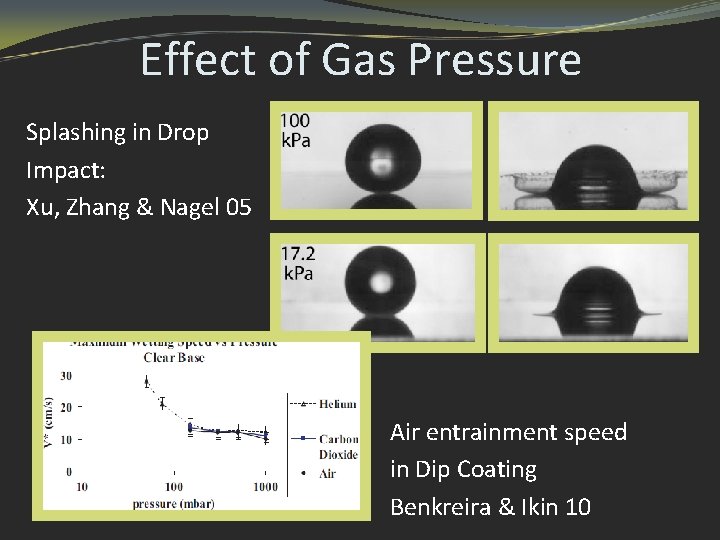
Effect of Gas Pressure Splashing in Drop Impact: Xu, Zhang & Nagel 05 Air entrainment speed in Dip Coating Benkreira & Ikin 10

Microdrop Impact 25 micron water drop impacting at 5 m/s on left: wettable substrate right: nonwettable substrate

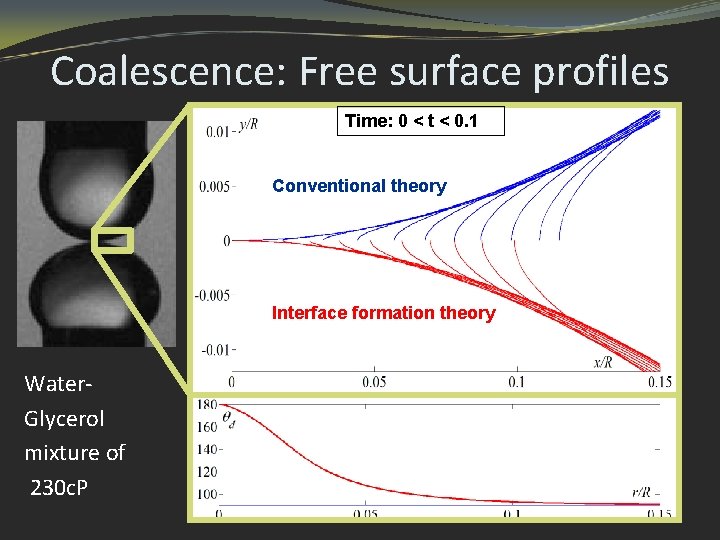
Coalescence: Free surface profiles Time: 0 < t < 0. 1 Conventional theory Interface formation theory Water. Glycerol mixture of 230 c. P

Appearance of V’s Impact of a solid sphere: Duez, Ybert, Clanet & Bocquet 07 Dip coating experiments Courtesy of Terry Blake