Modelling and Simulating Social Systems with MATLAB Lesson

Modelling and Simulating Social Systems with MATLAB Lesson 2 – Statistical plotting and animation A. Johansson & W. Yu © ETH Zürich | Datum

Lesson 2 - Contents § Repetition § Statistical Plotting § Animation 2008 -02 -25 A. Johansson & M. Moussaid / andersj@ethz. ch mehdim@ethz. ch 2

Repetition § Creating a scalar: >> a=10 a = 10 2008 -02 -25 A. Johansson & M. Moussaid / andersj@ethz. ch mehdim@ethz. ch 3

Repetition § Creating a row vector: >> v=[1 2 3 4 5] v = 1 2 3 4 5 2008 -02 -25 A. Johansson & M. Moussaid / andersj@ethz. ch mehdim@ethz. ch 4

Repetition § Creating a row vector, 2 nd method: >> v=1: 5 v = 1 2 3 4 5 2008 -02 -25 A. Johansson & M. Moussaid / andersj@ethz. ch mehdim@ethz. ch 5

Repetition § Creating a column vector: >> v=[1; 2; 3; 4; 5] v = 1 2 3 4 5 2008 -02 -25 A. Johansson & M. Moussaid / andersj@ethz. ch mehdim@ethz. ch 6

Repetition § Creating a column vector, 2 nd method: >> v=[1 2 3 4 5]’ v = 1 2 3 4 5 2008 -02 -25 A. Johansson & M. Moussaid / andersj@ethz. ch mehdim@ethz. ch 7

Repetition § Creating a matrix: >> A=[1 2 3 4; 5 6 7 8] A = 1 2 3 4 5 6 7 8 2008 -02 -25 A. Johansson & M. Moussaid / andersj@ethz. ch mehdim@ethz. ch 8

Repetition § Creating a matrix, 2 nd method: >> A=[1: 4; 5: 8] A = 1 2 3 4 5 6 7 8 2008 -02 -25 A. Johansson & M. Moussaid / andersj@ethz. ch mehdim@ethz. ch 9

Repetition § Accessing a scalar: >> a a = 10 2008 -02 -25 A. Johansson & M. Moussaid / andersj@ethz. ch mehdim@ethz. ch 10

Repetition § Accessing an element in a vector: v(index) >> v(2) ans = 2 2008 -02 -25 A. Johansson & M. Moussaid / andersj@ethz. ch mehdim@ethz. ch 11

Repetition § Accessing an element in a matrix: M(row. Index, column. Index) >> A(2, 1) ans = 5 2008 -02 -25 A. Johansson & M. Moussaid / andersj@ethz. ch mehdim@ethz. ch 12

Repetition - operators § Scalar operators: Basic: +, -, *, / Exponentialisation: ^ Square root: sqrt() 2008 -02 -25 A. Johansson & M. Moussaid / andersj@ethz. ch mehdim@ethz. ch 13

Repetition - operators § Matrix operators: Basic: +, -, * § Element-wise operators: Multiplication: . * Division: . / Exponentialisation: . ^ § Solving Ax=b: x = Ab 2008 -02 -25 A. Johansson & M. Moussaid / andersj@ethz. ch mehdim@ethz. ch 14

Repetition – for loop § Computation can be automized with for loops: >> y=0; for x=1: 4 y = y + x^2 + x; end >> y y = 40 2008 -02 -25 A. Johansson & M. Moussaid / andersj@ethz. ch mehdim@ethz. ch 15

Repetition – if case § Conditional computation can be made with if: >> val=-4; if (val>0 ) abs. Val = val; else abs. Val = -val; end 2008 -02 -25 A. Johansson & M. Moussaid / andersj@ethz. ch mehdim@ethz. ch 16

Statistics Function § Statistics in MATLAB can be performed with the following commands: Mean value: mean(x) Median value: median(x) Min/max values: min(x), max(x) Standard deviation: std(x) Variance: var(x) Covariance: cov(x) Correlation coefficient: corrcoef(x) 2008 -02 -25 A. Johansson & M. Moussaid / andersj@ethz. ch mehdim@ethz. ch 17

Plotting Function § Plotting in MATLAB can be performed with the following commands: Plot vector x vs. vector y: Linear scale: plot(x, y) Logarithmic scale: loglog(x, y) Plot histogram of x: hist(x) 2008 -02 -25 A. Johansson & M. Moussaid / andersj@ethz. ch mehdim@ethz. ch 18

Details of plot § An additional parameter can be provided to plot() to define how the curve will look like: plot(x, y, ‘key’) Where key is a string which can contain: Color codes: ‘r’, ‘g’, ‘b’, ‘k’, ‘y’, … Line codes: ‘-’, ‘--’ (solid, dashed, etc. ) Marker codes: ‘*’, ‘s’, ’c’ Examples: plot(x, y, ‘r--’) plot(x, y, ‘g*’) * * 2008 -02 -25 A. Johansson & M. Moussaid / andersj@ethz. ch mehdim@ethz. ch 19

Where can I get help? § >>help functionname § >>helpwin 2008 -02 -25 A. Johansson & M. Moussaid / andersj@ethz. ch mehdim@ethz. ch 20

Plotting Tips § To make the plots look nicer, the following commands can be used: Set label on x axis: xlabel(“text”) Set label on y axis: ylabel(“text”) Set title: title(“text”) 2008 -02 -25 A. Johansson & M. Moussaid / andersj@ethz. ch mehdim@ethz. ch 21

Plotting Tips § Two additional useful commands hold on|off § grid on|off § >> x=[-5: 0. 1: 5]; a=2; b=3; >> y 1=exp(-x. ^2); >> y 2=a*exp(-x. ^2); >> y 3=exp(-(x. ^2)/b); 2008 -02 -25 A. Johansson & M. Moussaid / andersj@ethz. ch mehdim@ethz. ch 22

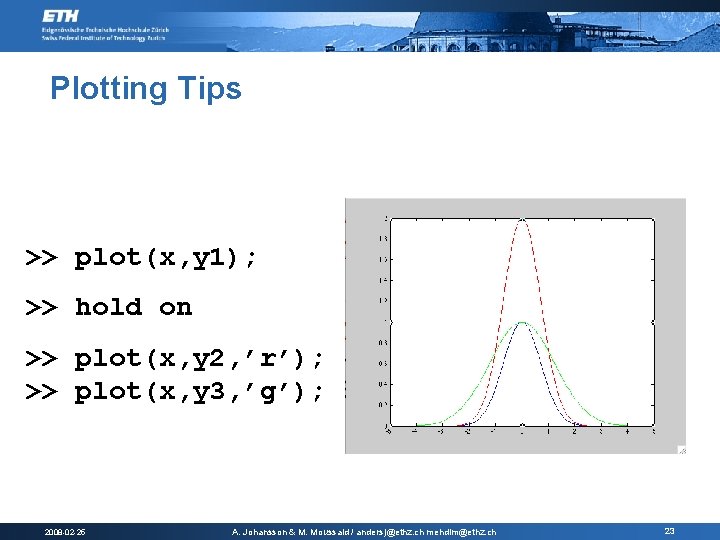
Plotting Tips >> plot(x, y 1); >> hold on >> plot(x, y 2, ’r’); >> plot(x, y 3, ’g’); 2008 -02 -25 A. Johansson & M. Moussaid / andersj@ethz. ch mehdim@ethz. ch 23

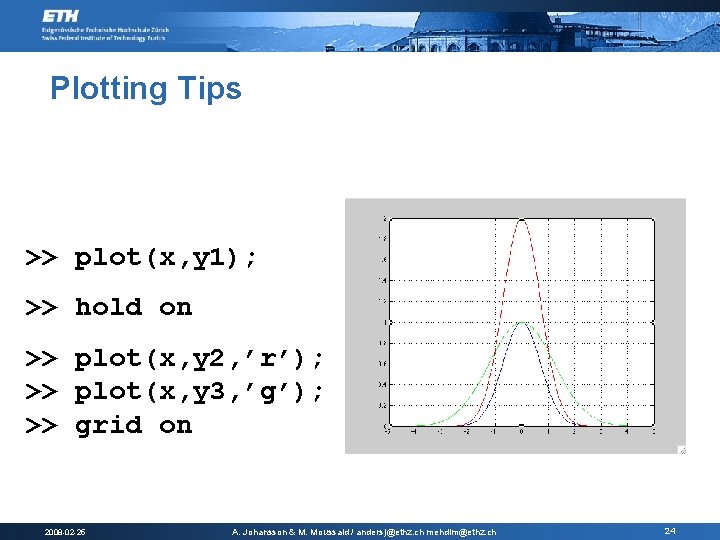
Plotting Tips >> plot(x, y 1); >> hold on >> plot(x, y 2, ’r’); >> plot(x, y 3, ’g’); >> grid on 2008 -02 -25 A. Johansson & M. Moussaid / andersj@ethz. ch mehdim@ethz. ch 24

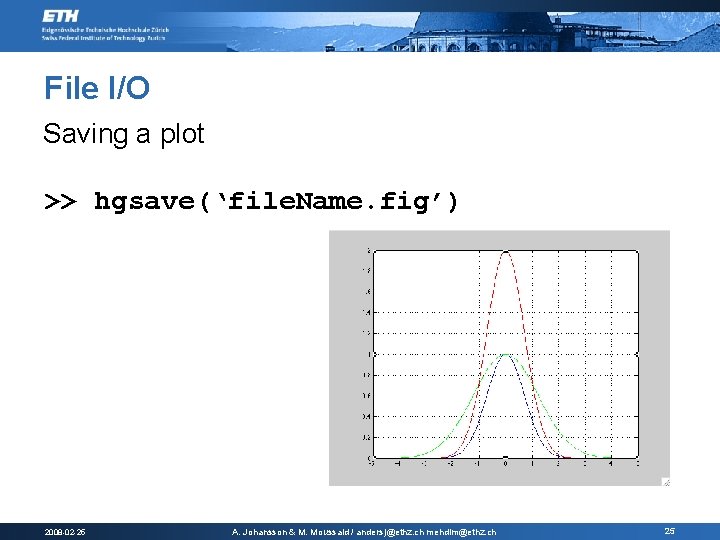
File I/O Saving a plot >> hgsave(‘file. Name. fig’) 2008 -02 -25 A. Johansson & M. Moussaid / andersj@ethz. ch mehdim@ethz. ch 25

Tips for I/O § Some commands in Linux are also applicable in Matlab. rmdir, mkdir § delete, edit § ls, cd § Tab § 2008 -02 -25 A. Johansson & M. Moussaid / andersj@ethz. ch mehdim@ethz. ch 26

Animation § A simple example of computer animation. r = 10; k = 1; pi = 3. 14; hold on; for t = 0 : 0. 01 : 2*pi x = r*cos(t); y = r*sin(t); plot(x, y, 'o', 'Marker. Size', 20); axis([-10, 10]); %adjust the range of axis M(k) = getframe; %get the current frame k = k+1; end%for 2008 -02 -25 A. Johansson & M. Moussaid / andersj@ethz. ch mehdim@ethz. ch 27

Replay a Movie § movie(M, N) plays the movie in matrix M for N times. 2008 -02 -25 A. Johansson & M. Moussaid / andersj@ethz. ch mehdim@ethz. ch 28

Save Movie as avi File § movie 2 avi(M, ’demo. avi’) saves the movie in matrix M as ‘demo. avi’. 2008 -02 -25 A. Johansson & M. Moussaid / andersj@ethz. ch mehdim@ethz. ch 29

3 Dimensions Plots § Plot a surface § surf(X, Y, Z) with: § X a vector containing the x-axis § Y a vector containing the y-axis § Z a matrix with Z(i, j) is the corresponding value for Y(i) and X(j) § Number of lines and columns in Z must respectively equal length(Y) and length(X). x 1 x 2 x 3 y 1 y 2 y 3 2008 -02 -25 z 11 z 12 z 13 z 21 z 22 z 23 z 31 z 32 z 33 A. Johansson & M. Moussaid / andersj@ethz. ch mehdim@ethz. ch 30

3 Dimensions Plots § Plot a surface >> X=-2: 0. 1: 2; >> Y=0: 0. 1: 1; >> Z = Y(2)*exp(-X. ^2) Z = 0. 0018 0. 0027 0. 0039 0. 0056 >> for i=1: length(Y) Z(i, : )= Y(i)*exp(-X. ^2); end 2008 -02 -25 A. Johansson & M. Moussaid / andersj@ethz. ch mehdim@ethz. ch 31

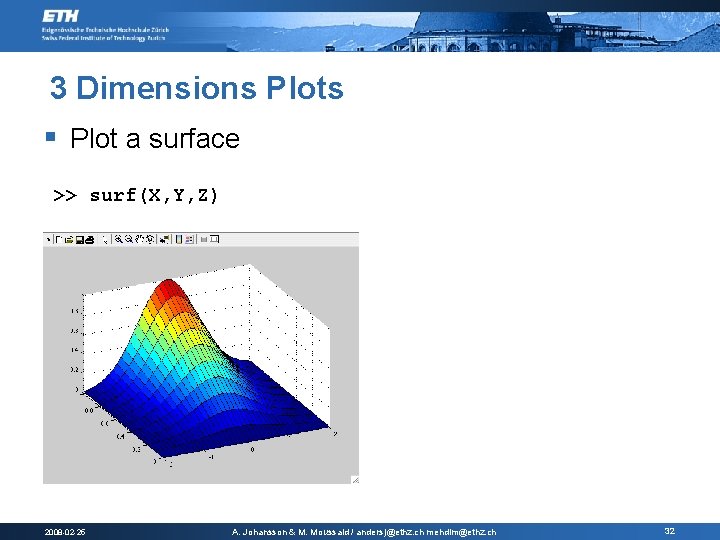
3 Dimensions Plots § Plot a surface >> surf(X, Y, Z) 2008 -02 -25 A. Johansson & M. Moussaid / andersj@ethz. ch mehdim@ethz. ch 32

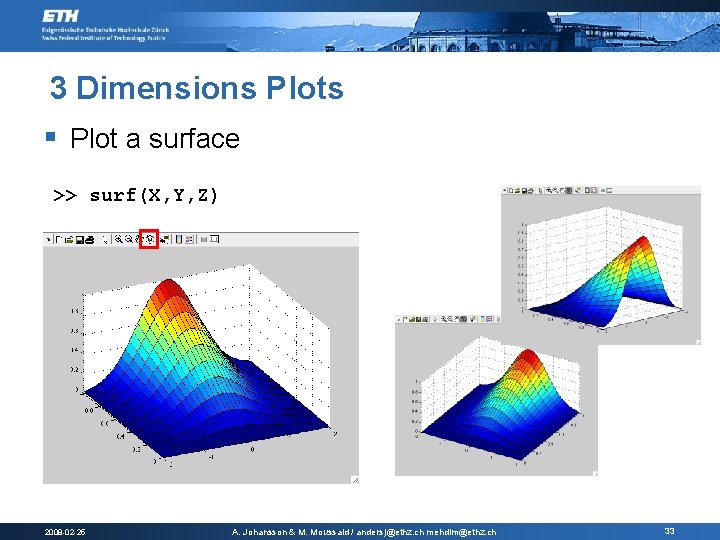
3 Dimensions Plots § Plot a surface >> surf(X, Y, Z) 2008 -02 -25 A. Johansson & M. Moussaid / andersj@ethz. ch mehdim@ethz. ch 33

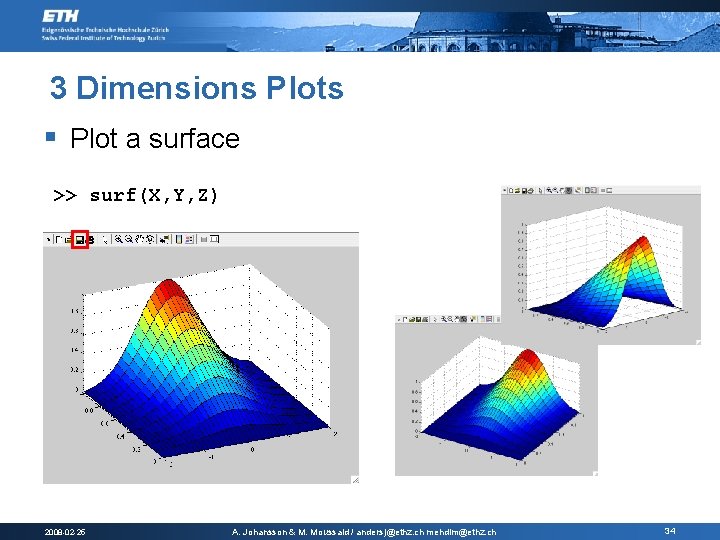
3 Dimensions Plots § Plot a surface >> surf(X, Y, Z) 2008 -02 -25 A. Johansson & M. Moussaid / andersj@ethz. ch mehdim@ethz. ch 34

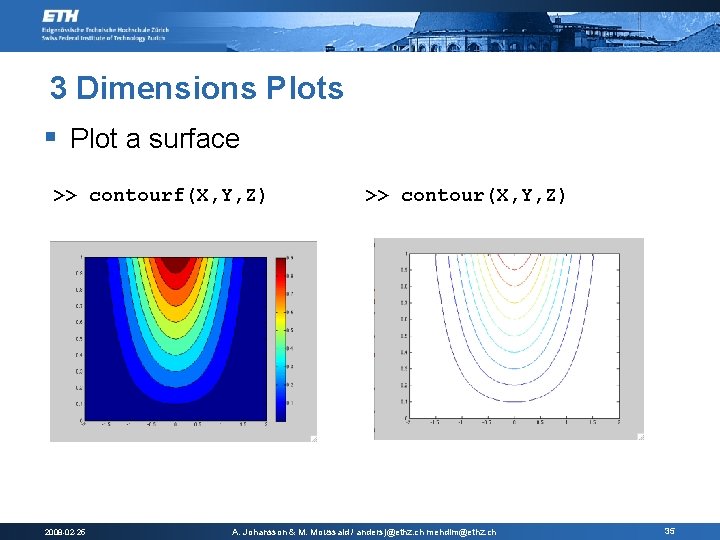
3 Dimensions Plots § Plot a surface >> contourf(X, Y, Z) 2008 -02 -25 >> contour(X, Y, Z) A. Johansson & M. Moussaid / andersj@ethz. ch mehdim@ethz. ch 35

Datasets § The datasets for statistical plotting can be found at the course web page http: //www. soms. ethz. ch/matlab you will find the files: countries. m cities. m 2008 -02 -25 A. Johansson & M. Moussaid / andersj@ethz. ch mehdim@ethz. ch 36

Datasets § Download the files countries. m and cities. m and save them in the working directory of MATLAB. 2008 -02 -25 A. Johansson & M. Moussaid / andersj@ethz. ch mehdim@ethz. ch 37

Datasets - countries § This dataset countries. m contains a matrix A with the following specification: § Rows: Different countries § Column 1: Population § Column 2: Annual growth (%) § Column 3: Percentage of youth § Column 4: Life expectancy (years) § Column 5: Mortality 2008 -02 -25 A. Johansson & M. Moussaid / andersj@ethz. ch mehdim@ethz. ch 38

Datasets - countries § Most often, we want to access complete columns in the matrix. This can be done by A(: , index) For example if you are interested in the lifeexpectancy column, it is recommended to do: >> life = x(: , 4); and then the vector life can be used to access the vector containing all life expectancies. 2008 -02 -25 A. Johansson & M. Moussaid / andersj@ethz. ch mehdim@ethz. ch 39

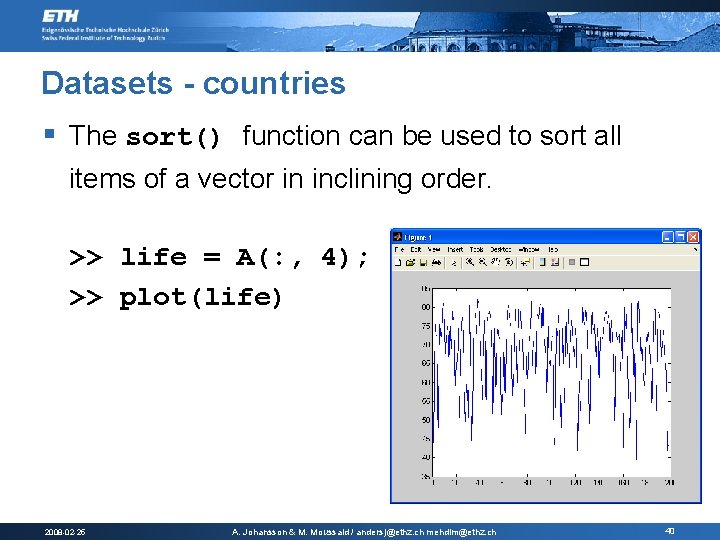
Datasets - countries § The sort() function can be used to sort all items of a vector in inclining order. >> life = A(: , 4); >> plot(life) 2008 -02 -25 A. Johansson & M. Moussaid / andersj@ethz. ch mehdim@ethz. ch 40

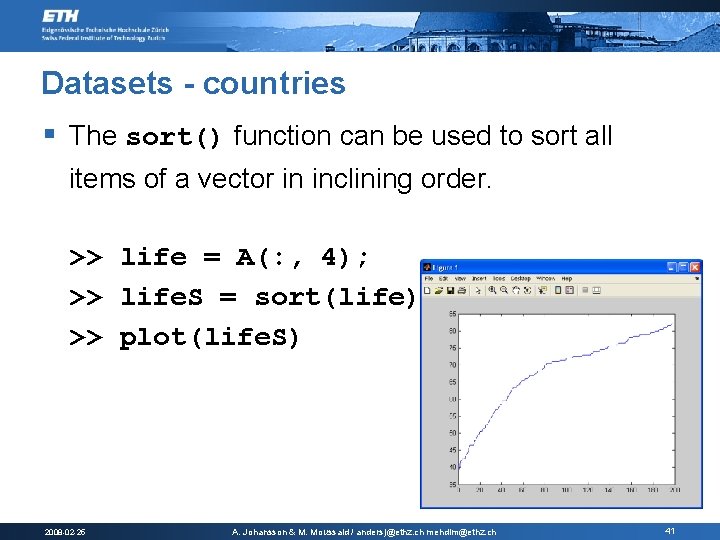
Datasets - countries § The sort() function can be used to sort all items of a vector in inclining order. >> life = A(: , 4); >> life. S = sort(life); >> plot(life. S) 2008 -02 -25 A. Johansson & M. Moussaid / andersj@ethz. ch mehdim@ethz. ch 41

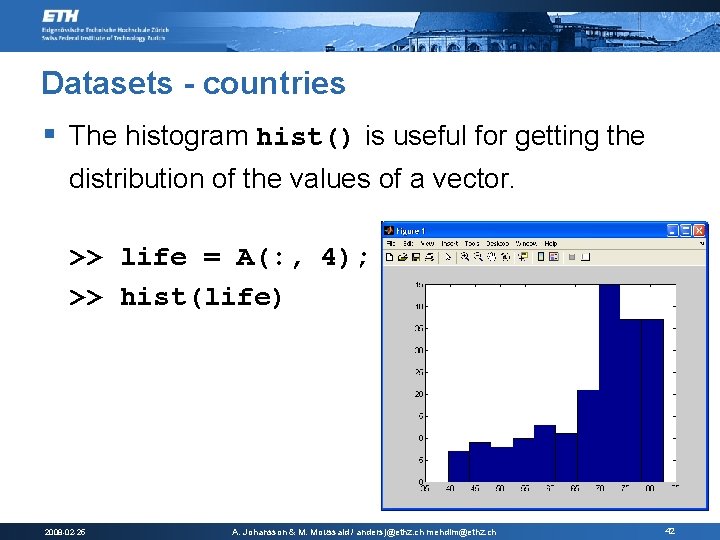
Datasets - countries § The histogram hist() is useful for getting the distribution of the values of a vector. >> life = A(: , 4); >> hist(life) 2008 -02 -25 A. Johansson & M. Moussaid / andersj@ethz. ch mehdim@ethz. ch 42

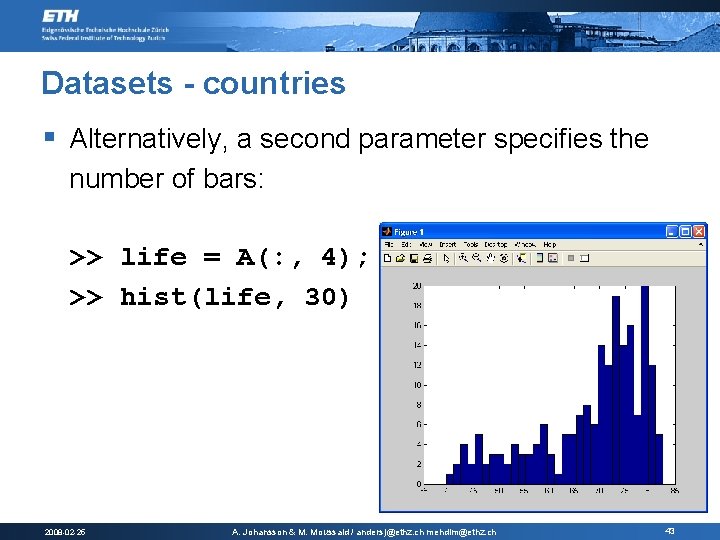
Datasets - countries § Alternatively, a second parameter specifies the number of bars: >> life = A(: , 4); >> hist(life, 30) 2008 -02 -25 A. Johansson & M. Moussaid / andersj@ethz. ch mehdim@ethz. ch 43

Exercise 1 § Statistics: Generate a vector of N random numbers with randn(N, 1) Calculate the mean and standard deviation. Do the mean and standard deviation converge to certain values, for an increasing N? Optional: Display the histogram with hist(randn(N, 1)) and compare with the histogram of rand() 2008 -02 -25 A. Johansson & M. Moussaid / andersj@ethz. ch mehdim@ethz. ch 44

Exercise 2 § Demographics: From the countries. m dataset, find out why there is such a large difference between the mean and the median population of all countries. Hint: Use hist(x, n) Also sort() can be useful. 2008 -02 -25 A. Johansson & M. Moussaid / andersj@ethz. ch mehdim@ethz. ch 45

Exercise 3 § Demographics: From the countries. m dataset, see which columns have strongest correlation. Can you reason why these columns have stronger correlations? Hint: Use corrcoef() to find the correlation between columns. 2008 -02 -25 A. Johansson & M. Moussaid / andersj@ethz. ch mehdim@ethz. ch 46

Exercise 4 - optional § Zipf’s law: Zipf’s law says that the rank, x, of cities (1: largest, 2: 2 nd largest, 3: 3 rd largest, . . . ) and the size, y, of cities (population) has a power-law relation: y ~ xb Test if Zipf’s law holds for the three cases in the cities. m file. Try to estimate the b parameter. Hint: Use log() and plot() (or loglog()) 2008 -02 -25 A. Johansson & M. Moussaid / andersj@ethz. ch mehdim@ethz. ch 47