Modellierung von Mehrkrpersystemen In dieser Vorlesung werden einige

Modellierung von Mehrkörpersystemen • In dieser Vorlesung werden einige spezielle Probleme behandelt, die Modellierung komplexer mechanischer Systeme begleiten. • Es wird erklärt, wie diese Probleme in Dymola angegangen worden sind. • Insbesondere wird die Wahl der Zustandsvariablen und der Konnektoren erläutert. • Es wird aufgezeigt, wie Matrizenkalkül es ermöglicht, die Definitionen äusserst kompakt zu halten. 17. November, 2004 Anfang Präsentation

Übersicht • • 17. November, 2004 Mehrkörpersysteme Wahl der Zustandsvariabeln Kinematische Schleifen Mechanische Konnektoren Mechanische Körper Mechanische Gelenke Beispiel Anfang Präsentation

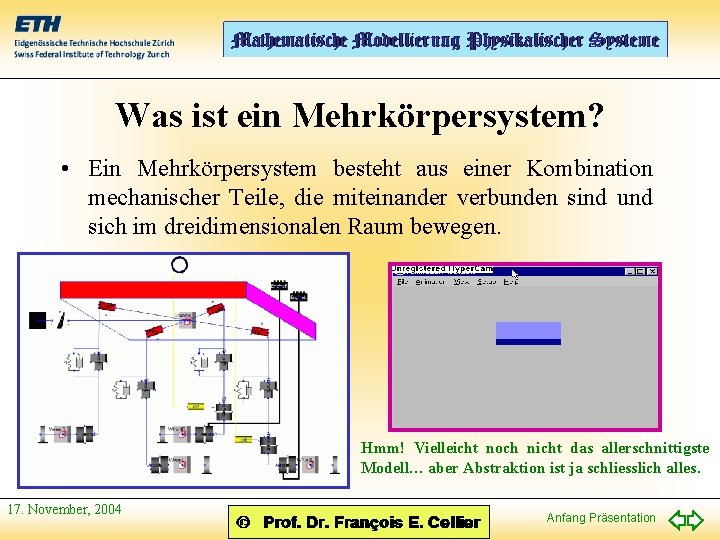
Was ist ein Mehrkörpersystem? • Ein Mehrkörpersystem besteht aus einer Kombination mechanischer Teile, die miteinander verbunden sind und sich im dreidimensionalen Raum bewegen. Hmm! Vielleicht noch nicht das allerschnittigste Modell… aber Abstraktion ist ja schliesslich alles. 17. November, 2004 Anfang Präsentation

Die Wahl der Zustandsvariablen • Bisher wurden bei den mechanischen Systemen, die wir betrachtet haben, die Differentialgleichungen immer mit den Massen gekoppelt. Dies schien sinnvoll zu sein, da das D’Alembert’sche Prinzip ja für die einzelnen Massen definiert werden muss. • Eine Masse, die fest mit der Erde (d. h. mit dem Inertialsystem) verankert ist, führt aber nicht zu Differentialgleichungen gibt es erst, wenn sich die Masse relativ zum Inertialsystem bewegt. • Somit mag es sinnvoller sein, die Integratoren mit den Relativbewegungen zwischen Körpern zu identifizieren. Dies wurde in der Mehrkörpersystembibliothek (MKS Bibliothek) von Dymola auch so implementiert. • In der MKS Bibliothek werden die Relativpositionen und Relativgeschwindigkeiten zwischen miteinander verbundenen Körpern als Zustandsvariabeln definiert. 17. November, 2004 Anfang Präsentation

Strukturelle Singularitäten I • Bei der getroffenen Wahl der Zustandsvariablen ergeben sich keine strukturellen Singularitäten bei Mehrkörpersystemen in Baumstruktur. • Bei kinematisch geschlossenen Schleifen ergeben sich strukturelle Singularitäten, da solche Strukturen weniger Freiheitsgrade aufweisen als Verbindungen zwischen benachbarten Körpern. Man denke zum Beispiel ans Scherengitter, welches nur einen Freiheitsgrad aufweist. y x 17. November, 2004 Kinematisch geschlossene Schleifen Anfang Präsentation

Strukturelle Singularitäten II • Um die strukturellen Singularitäten zu vermeiden, wird eines der Gelenke bei jeder kinematisch geschlossenen Schleife als Schneidegelenk (“cut joint”) definiert. y x Schneidegelenke • Schneidegelenke definieren keine Integratoren und vermeiden dadurch die Einführung struktureller Singularitäten. Dies ist effizienter, als sich auf den Pantelides Algorithmus zu verlassen. 17. November, 2004 Anfang Präsentation

Algebraische Schleifen • Geschlossene kinematische Schleifen führen unweigerlich auch zu bösen algebraischen Schleifen in den resultierenden Gleichungssystemen. Diese sind normalerweise sehr gross, da sie sich über alle Variablen der kinematischen Schleife erstrecken. • Das automatische Auffinden geeigneter Schneidevariablen ist teuer und ineffizient. • Die Schneidegelenke von Dymola enthalten Anweisungen, die es dem Schneidealgorithmus ermöglichen, schnell geeignete Schneidevariablen zu ermitteln. constrain(q, qdd) 17. November, 2004 Anfang Präsentation

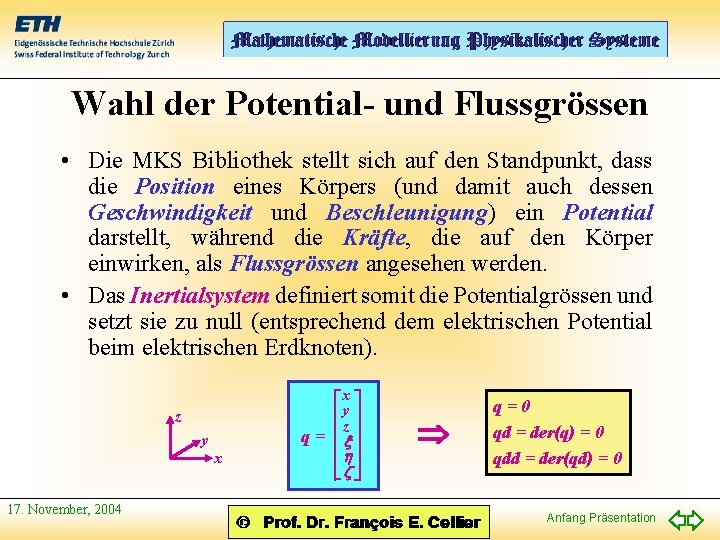
Wahl der Potential- und Flussgrössen • Die MKS Bibliothek stellt sich auf den Standpunkt, dass die Position eines Körpers (und damit auch dessen Geschwindigkeit und Beschleunigung) ein Potential darstellt, während die Kräfte, die auf den Körper einwirken, als Flussgrössen angesehen werden. • Das Inertialsystem definiert somit die Potentialgrössen und setzt sie zu null (entsprechend dem elektrischen Potential beim elektrischen Erdknoten). z q= y x 17. November, 2004 x y z q=0 qd = der(q) = 0 qdd = der(qd) = 0 Anfang Präsentation

Mechanische Konnektoren connector Frame Position r 0[3] "Abstand des Frames vom Inertialsystem"; Real S[3, 3] "Transformationsmatrix des Frames zum Inertialsystem"; Velocity v[3] "Absolute Geschwindigkeit des Frames"; Angular. Velocity w[3] "Absolute Winkelgeschwindigkeit des Frames"; Acceleration a[3] "Absolute Beschleunigung des Frames"; Angular. Acceleration z[3] "Absolute Winkelbeschleunigung des Frames"; flow Force f[3] "Am Frame angreifende Kraft"; flow Torque t[3] "Am Frame angreifendes Drehmoment"; end Frame; Wegen der Vorzeichenkonventionen muss immer ein ungefülltes Ausgangsframe ( ) zu einem gefüllten Eingangsframe ( ) verbunden werden. 17. November, 2004 Anfang Präsentation

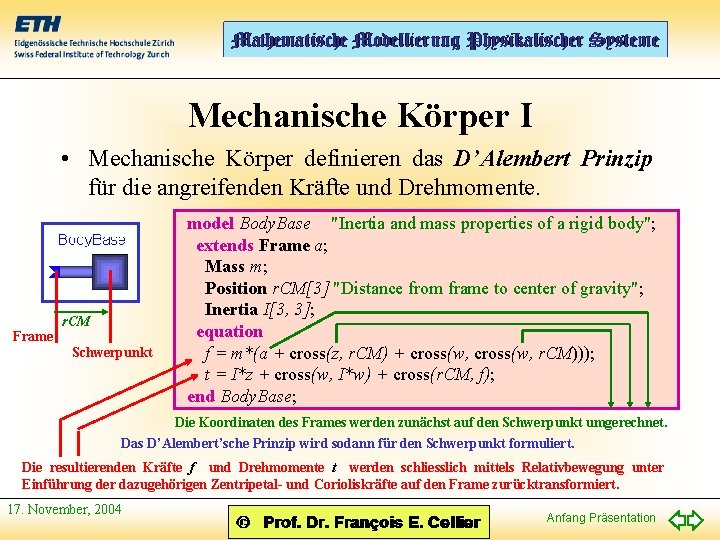
Mechanische Körper I • Mechanische Körper definieren das D’Alembert Prinzip für die angreifenden Kräfte und Drehmomente. Frame r. CM Schwerpunkt model Body. Base "Inertia and mass properties of a rigid body"; extends Frame a; Mass m; Position r. CM[3] "Distance from frame to center of gravity"; Inertia I[3, 3]; equation f = m*(a + cross(z, r. CM) + cross(w, r. CM))); t = I*z + cross(w, I*w) + cross(r. CM, f); end Body. Base; Die Koordinaten des Frames werden zunächst auf den Schwerpunkt umgerechnet. Das D’Alembert’sche Prinzip wird sodann für den Schwerpunkt formuliert. Die resultierenden Kräfte f und Drehmomente t werden schliesslich mittels Relativbewegung unter Einführung der dazugehörigen Zentripetal- und Corioliskräfte auf den Frame zurücktransformiert. 17. November, 2004 Anfang Präsentation

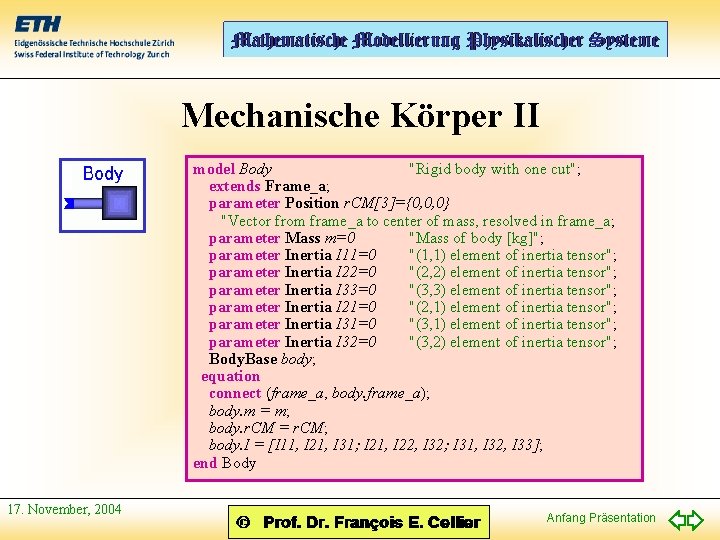
Mechanische Körper II model Body "Rigid body with one cut"; extends Frame_a; parameter Position r. CM[3]={0, 0, 0} "Vector from frame_a to center of mass, resolved in frame_a; parameter Mass m=0 "Mass of body [kg]"; parameter Inertia I 11=0 "(1, 1) element of inertia tensor"; parameter Inertia I 22=0 "(2, 2) element of inertia tensor"; parameter Inertia I 33=0 "(3, 3) element of inertia tensor"; parameter Inertia I 21=0 "(2, 1) element of inertia tensor"; parameter Inertia I 31=0 "(3, 1) element of inertia tensor"; parameter Inertia I 32=0 "(3, 2) element of inertia tensor"; Body. Base body; equation connect (frame_a, body. frame_a); body. m = m; body. r. CM = r. CM; body. I = [I 11, I 21, I 31; I 21, I 22, I 32; I 31, I 32, I 33]; end Body 17. November, 2004 Anfang Präsentation

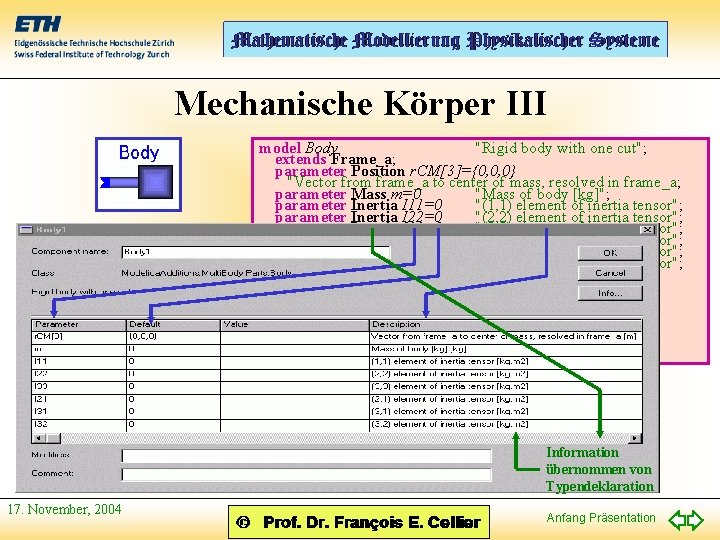
Mechanische Körper III model Body "Rigid body with one cut"; extends Frame_a; parameter Position r. CM[3]={0, 0, 0} "Vector from frame_a to center of mass, resolved in frame_a; parameter Mass m=0 "Mass of body [kg]"; parameter Inertia I 11=0 "(1, 1) element of inertia tensor"; parameter Inertia I 22=0 "(2, 2) element of inertia tensor"; parameter Inertia I 33=0 "(3, 3) element of inertia tensor"; parameter Inertia I 21=0 "(2, 1) element of inertia tensor"; parameter Inertia I 31=0 "(3, 1) element of inertia tensor"; parameter Inertia I 32=0 "(3, 2) element of inertia tensor"; Body. Base body; equation connect (frame_a, body. frame_a); body. m = m; body. r. CM = r. CM; body. I = [I 11, I 21, I 31; I 21, I 22, I 32; I 31, I 32, I 33]; end Body Information übernommen von Typendeklaration 17. November, 2004 Anfang Präsentation

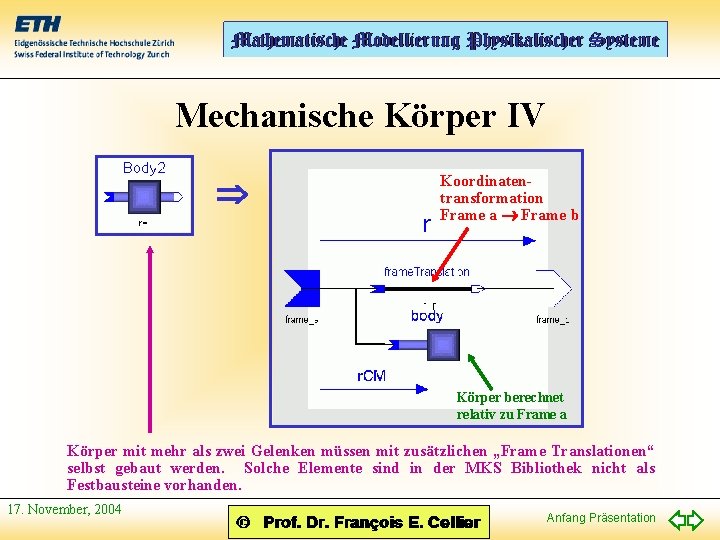
Mechanische Körper IV Koordinatentransformation Frame a Frame b Körper berechnet relativ zu Frame a Körper mit mehr als zwei Gelenken müssen mit zusätzlichen „Frame Translationen“ selbst gebaut werden. Solche Elemente sind in der MKS Bibliothek nicht als Festbausteine vorhanden. 17. November, 2004 Anfang Präsentation

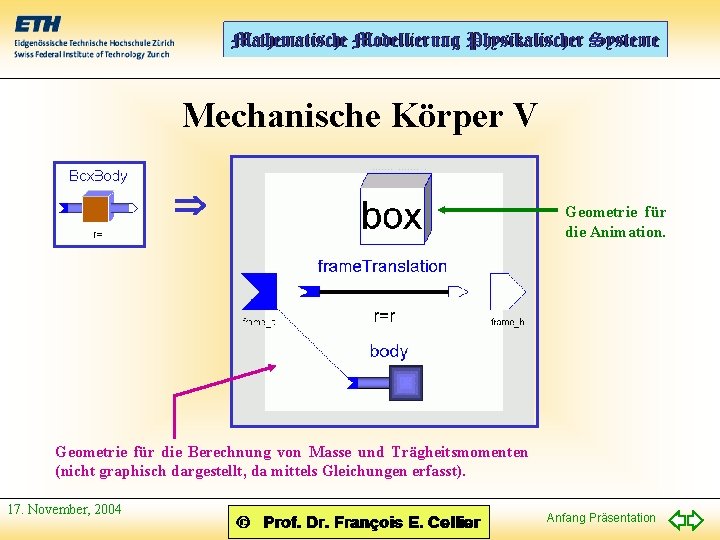
Mechanische Körper V Geometrie für die Animation. Geometrie für die Berechnung von Masse und Trägheitsmomenten (nicht graphisch dargestellt, da mittels Gleichungen erfasst). 17. November, 2004 Anfang Präsentation

Mechanische Körper VI model Box. Body "Rigid body with box shape (also used for animation)" extends Multi. Body. Interfaces. Two. Tree. Frames; parameter SIunits. Position r[3]={0. 1, 0, 0} "Vector from frame_a to frame_b, resolved in frame_a"; parameter SIunits. Position r 0[3]={0, 0, 0} "Vector from frame_a to left box plane, resolved in frame_a"; parameter SIunits. Position Length. Direction[3]=r - r 0 "Vector in length direction, resolved in frame_a"; parameter SIunits. Position Width. Direction[3]={0, 1, 0} "Vector in width direction, resolved in frame_a"; parameter SIunits. Length=(sqrt((r - r 0)*(r - r 0))) "Length of box"; parameter SIunits. Length Width=0. 1 "Width of box"; parameter SIunits. Length Height=0. 1 "Height of box"; parameter SIunits. Length Inner. Width=0 "Width of inner box surface"; parameter SIunits. Length Inner. Height=0 "Height of inner box surface"; parameter Real rho=7. 7 "Density of box material [g/cm^3]"; parameter Real Material[4]={1, 0, 0, 0. 5} "Color and specular coefficient"; SIunits. Mass mo, mi; Real Sbox[3, 3]; SIunits. Length l, w, h, wi, hi; Frame. Translation frame. Translation(r=r); Multi. Body. Interfaces. Body. Base body; Visual. Shape box (Shape="box", r 0=r 0, Length. Direction=Length. Direction, Width. Direction=Width. Direction, Length=Length, Width=Width, Height=Height, Material=Material); 17. November, 2004 Anfang Präsentation

Mechanische Körper VII equation connect (body. frame_a, frame_a); connect (frame_a, frame. Translation. frame_a); connect (frame. Translation. frame_b, frame_b); box. S = Sa; box. r = r 0 a; box. Sshape = Sbox; l = Length; w = Width; h = Height; wi = Inner. Width; hi = Inner. Height; /*Mass properties of box*/ mo = 1000*rho*l*w*h; mi = 1000*rho*l*wi*hi; body. m = mo - mi; body. r. CM = r 0 + l/2*box. n. Length; body. I = Sbox*diagonal({mo*(w*w + h*h) - mi*(wi*wi + hi*hi), mo*(l*l + h*h) - mi*(l*l + hi*hi), mo*(l*l + w*w) - mi*(l*l + wi*wi)}/12)*transpose(Sbox); end Box. Body 17. November, 2004 Anfang Präsentation

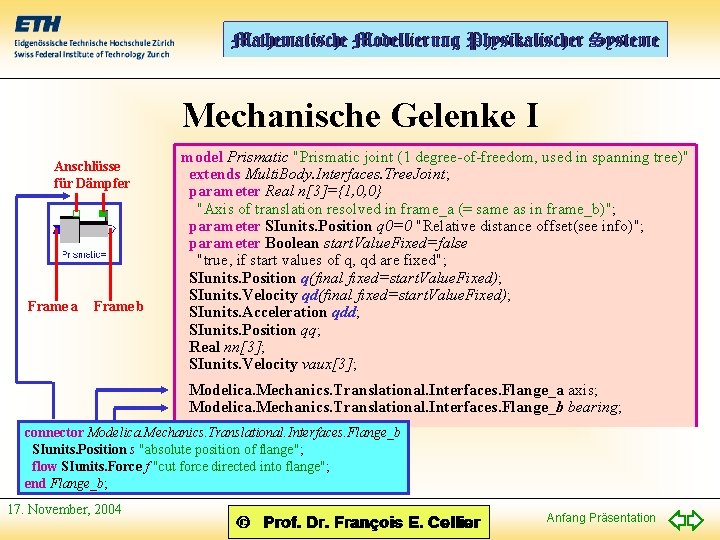
Mechanische Gelenke I Anschlüsse für Dämpfer Frame a Frame b model Prismatic "Prismatic joint (1 degree-of-freedom, used in spanning tree)" extends Multi. Body. Interfaces. Tree. Joint; parameter Real n[3]={1, 0, 0} "Axis of translation resolved in frame_a (= same as in frame_b)"; parameter SIunits. Position q 0=0 "Relative distance offset(see info)"; parameter Boolean start. Value. Fixed=false "true, if start values of q, qd are fixed"; SIunits. Position q(final fixed=start. Value. Fixed); SIunits. Velocity qd(final fixed=start. Value. Fixed); SIunits. Acceleration qdd; SIunits. Position qq; Real nn[3]; SIunits. Velocity vaux[3]; Modelica. Mechanics. Translational. Interfaces. Flange_a axis; Modelica. Mechanics. Translational. Interfaces. Flange_b bearing; connector Modelica. Mechanics. Translational. Interfaces. Flange_b SIunits. Position s "absolute position of flange"; flow SIunits. Force f "cut force directed into flange"; end Flange_b; 17. November, 2004 Anfang Präsentation

Mechanische Gelenke II equation axis. s = q; bearing. s = 0; // define states qd = der(q); qdd = der(qd); /*normalize axis vector*/ nn = n/sqrt(n*n); /*kinematic quantities*/ S_rel = identity(3); qq = q - q 0; r_rela = nn*qq; v_rela = nn*qd; a_rela = nn*qdd; w_rela = zeros(3); z_rela = zeros(3); 17. November, 2004 /* Transform the kinematic quantities from frame_a to frame_b and the force and torque acting at frame_b to frame_a (= general equations of a "Tree. Joint" specialized to this class). */ Sb = Sa; r 0 b = r 0 a + Sa*r_rela; vaux = cross(wa, r_rela); vb = va + v_rela + vaux; wb = wa; ab = aa + a_rela + cross(za, r_rela) + cross(wa, vaux + 2*v_rela); zb = za; fa = fb; ta = tb + cross(r_rela, fa); // d'Alemberts principle axis. f = nn*fb; end Prismatic Anfang Präsentation

Kausalitäten I • Die Kausalität der Gleichungen hängt ab vom gestellten Problem. • Beim direkten Problem (dem Simulationsproblem) sind die Kräfte und Drehmomente gegeben, während die Bewegung gesucht wird. • Beim inversen Problem (dem Planungsproblem) sind die gewünschten Bewegungen vorbestimmt, während die Kräfte und Drehmomente, die eingesetzt werden müssen, um die gewünschten Bewegungen zu erzielen, gesucht sind. 17. November, 2004 Anfang Präsentation

Kausalitäten II • Die Effizienz des erzeugten Codes hängt sehr stark von der Formulierung der Gleichungen ab. Kleine Änderungen der Formulierung können die Effizienz so verändern, dass die Anzahl resultierender Gleichungen am Ende entweder linear mit der Anzahl Körper steigt oder mit deren vierter Potenz. • Aus diesem Grund verlässt sich die MKS Bibliothek nicht auf die automatische Umwandlung der Gleichungen unter Verwendung des Pantelides Algorithmus und der Heuristiken zur Ermittlung kleiner Sätze von Schnitt-variablen. 17. November, 2004 Anfang Präsentation

Kausalitäten III • Die Matrizenschreibweise, die bisher verwendet wurde, ist zwar sehr elegant und kompakt und darum gut geeignet für den Unterhalt der MBS Bibliothek, sie eignet sich aber nicht für das automatische Umformen der Gleichungen. • Aus diesem Grund werden in Modelica alle Matrizengleichungen vor der Ermittlung der Kausalität symbolisch expandiert. 17. November, 2004 Anfang Präsentation

Ein Beispiel I 17. November, 2004 Anfang Präsentation

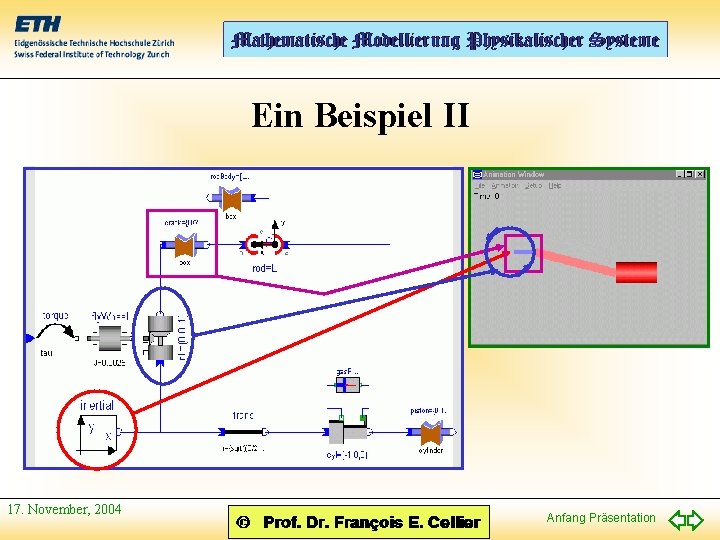
Ein Beispiel II 17. November, 2004 Anfang Präsentation

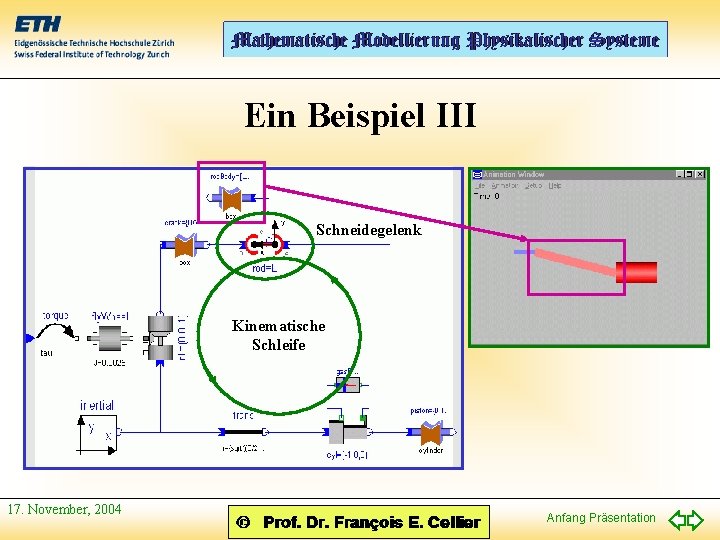
Ein Beispiel III Schneidegelenk Kinematische Schleife 17. November, 2004 Anfang Präsentation

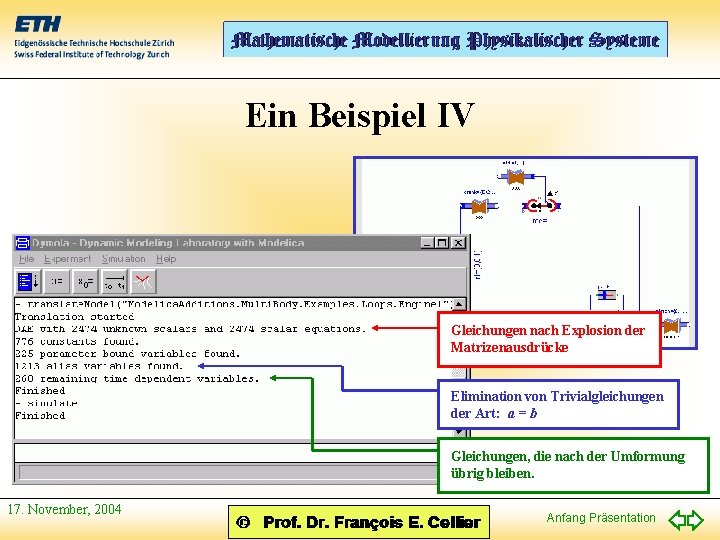
Ein Beispiel IV Gleichungen nach Explosion der Matrizenausdrücke Elimination von Trivialgleichungen der Art: a = b Gleichungen, die nach der Umformung übrig bleiben. 17. November, 2004 Anfang Präsentation

Ein Beispiel V 17. November, 2004 Anfang Präsentation

Referenzen • Otter, M. , H. Elmqvist, and F. E. Cellier (1996), “Modeling of Multibody Systems with the Object. Oriented Modeling Language Dymola, ” J. Nonlinear Dynamics, 9(1), pp. 91 -112. 17. November, 2004 Anfang Präsentation