Modelli dinamici di reattori ideali CORSO DI DINAMICA

Modelli dinamici di reattori ideali CORSO DI DINAMICA E CONTROLLO DEI SISTEMI E PROCESSI ENERGETICI A. A. 2016 -2017

Bilancio di materia � Il punto di partenza è il bilancio di materia per ogni reagente (o prodotto). Quando la composizione all’interno del reattore è uniforme (indipendente dalla posizione) il bilancio può essere eseguito per l’intero reattore; se la composizione non è uniforme il bilancio viene eseguito per un elemento infinitesimo di volume. velocità di ingresso del reagente nell’element o di volume = velocità di uscita del reagente dall’element o di volume + velocità di scomparsa del reagente per la reazione chimica nell’element o di volume + velocità di accumulo del reagente nell’element o di volume

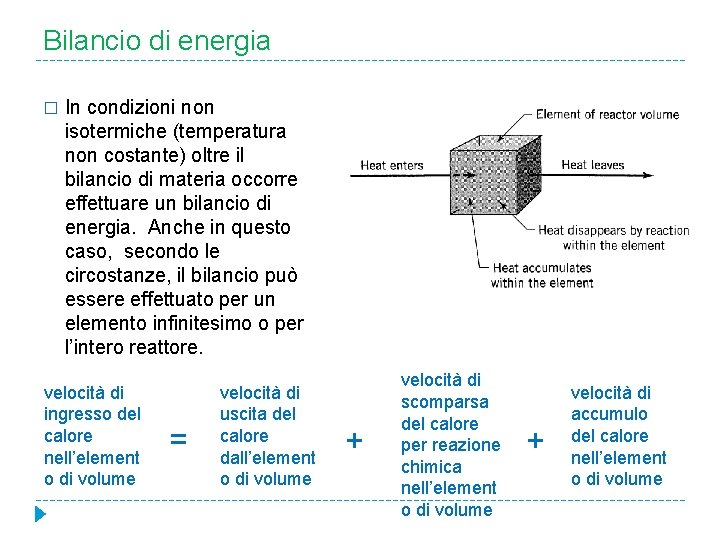
Bilancio di energia � In condizioni non isotermiche (temperatura non costante) oltre il bilancio di materia occorre effettuare un bilancio di energia. Anche in questo caso, secondo le circostanze, il bilancio può essere effettuato per un elemento infinitesimo o per l’intero reattore. velocità di ingresso del calore nell’element o di volume = velocità di uscita del calore dall’element o di volume + velocità di scomparsa del calore per reazione chimica nell’element o di volume + velocità di accumulo del calore nell’element o di volume

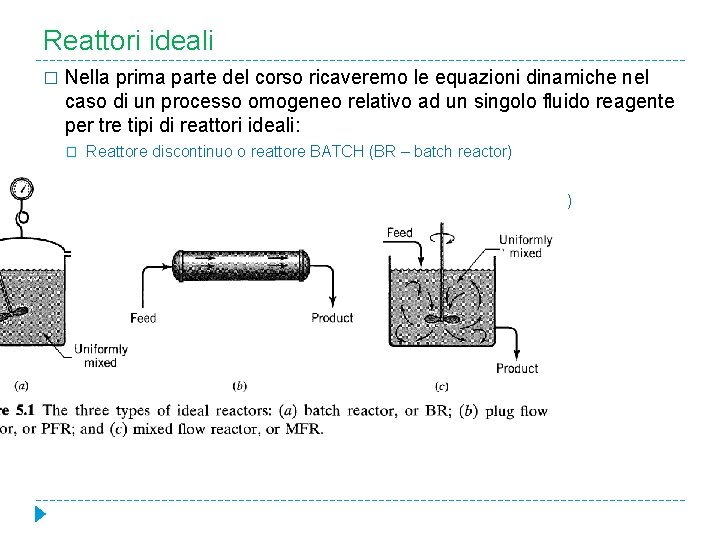
Reattori ideali � Nella prima parte del corso ricaveremo le equazioni dinamiche nel caso di un processo omogeneo relativo ad un singolo fluido reagente per tre tipi di reattori ideali: � Reattore discontinuo o reattore BATCH (BR – batch reactor) � Reattore con flusso a pistone (PFR – plug flow reactor) � Reattore a mescolamento (CSTR – continuously stirred tank reactor)

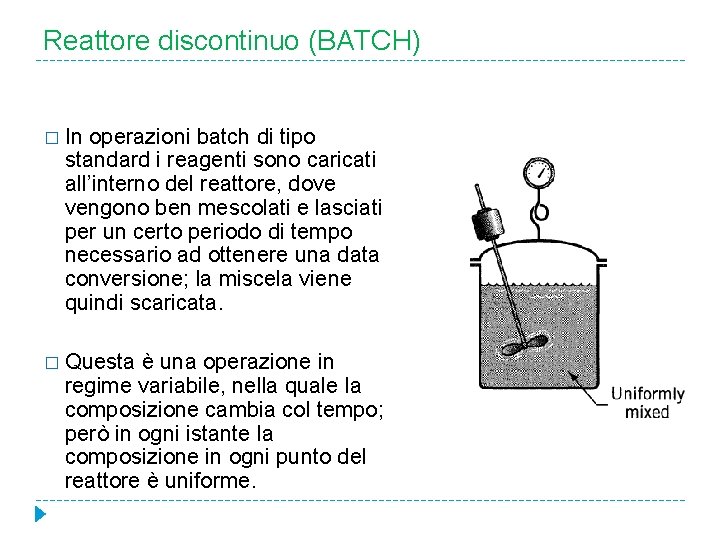
Reattore discontinuo (BATCH) � In operazioni batch di tipo standard i reagenti sono caricati all’interno del reattore, dove vengono ben mescolati e lasciati per un certo periodo di tempo necessario ad ottenere una data conversione; la miscela viene quindi scaricata. � Questa è una operazione in regime variabile, nella quale la composizione cambia col tempo; però in ogni istante la composizione in ogni punto del reattore è uniforme.

Reattore discontinuo alimentato (fed-BATCH) � In operazioni fed-BATCH i reagenti sono caricati A PIÙ RIPRESE nel reattore, dove vengono ben mescolati e lasciati per un certo periodo di tempo necessario ad ottenere una data conversione; la miscela viene quindi scaricata. � Questa è una operazione in regime variabile, nella quale la composizione cambia col tempo, SIA per effetto della reazione chimica SIA per effetto di successive alimentazioni. In ogni istante la composizione in ogni punto del reattore è uniforme.

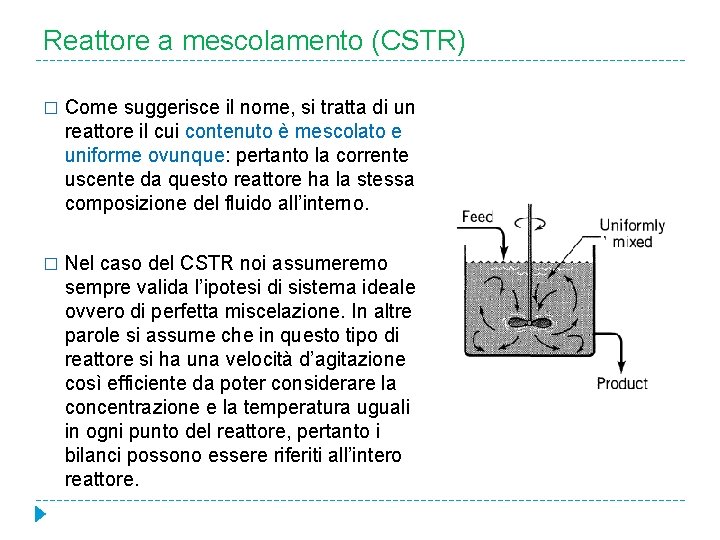
Reattore a mescolamento (CSTR) � Come suggerisce il nome, si tratta di un reattore il cui contenuto è mescolato e uniforme ovunque: pertanto la corrente uscente da questo reattore ha la stessa composizione del fluido all’interno. � Nel caso del CSTR noi assumeremo sempre valida l’ipotesi di sistema ideale ovvero di perfetta miscelazione. In altre parole si assume che in questo tipo di reattore si ha una velocità d’agitazione così efficiente da poter considerare la concentrazione e la temperatura uguali in ogni punto del reattore, pertanto i bilanci possono essere riferiti all’intero reattore.

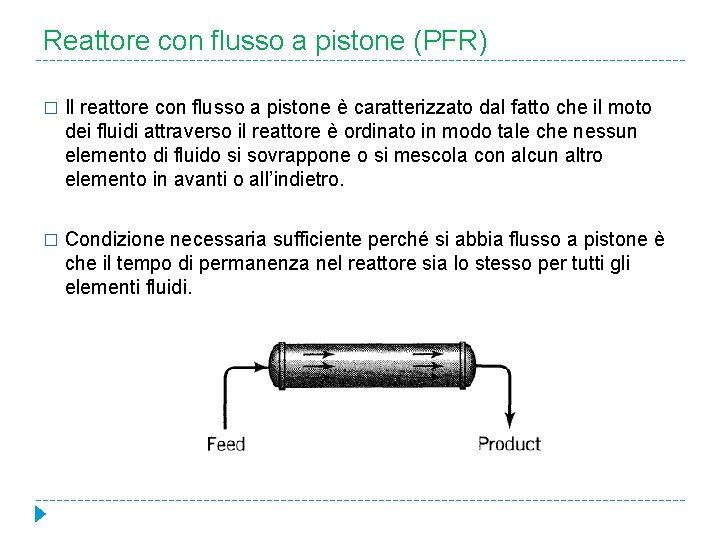
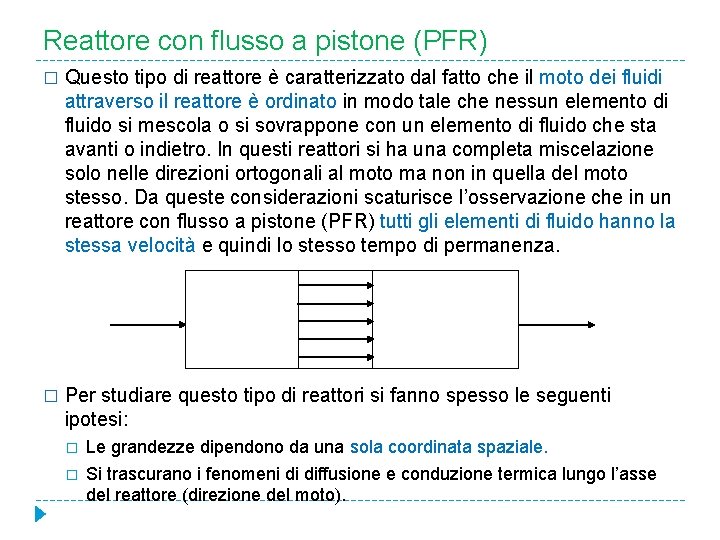
Reattore con flusso a pistone (PFR) � Il reattore con flusso a pistone è caratterizzato dal fatto che il moto dei fluidi attraverso il reattore è ordinato in modo tale che nessun elemento di fluido si sovrappone o si mescola con alcun altro elemento in avanti o all’indietro. � Condizione necessaria sufficiente perché si abbia flusso a pistone è che il tempo di permanenza nel reattore sia lo stesso per tutti gli elementi fluidi.

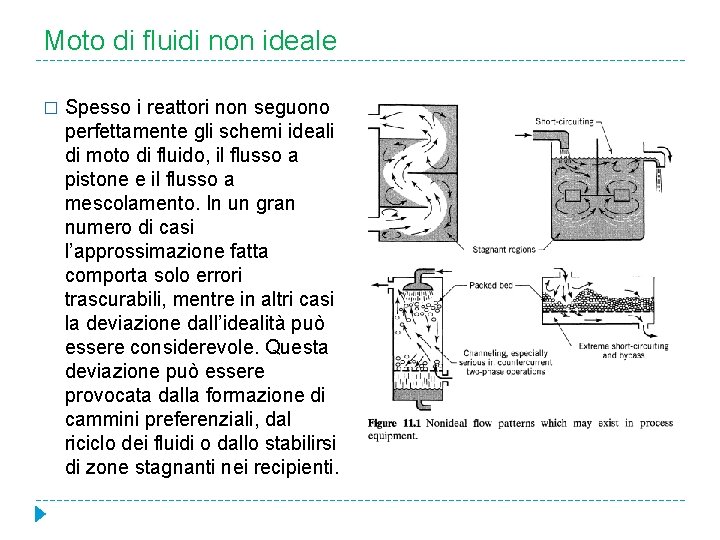
Moto di fluidi non ideale � Spesso i reattori non seguono perfettamente gli schemi ideali di moto di fluido, il flusso a pistone e il flusso a mescolamento. In un gran numero di casi l’approssimazione fatta comporta solo errori trascurabili, mentre in altri casi la deviazione dall’idealità può essere considerevole. Questa deviazione può essere provocata dalla formazione di cammini preferenziali, dal riciclo dei fluidi o dallo stabilirsi di zone stagnanti nei recipienti.

Reattori eterogenei

Reattore a mescolamento CSTR

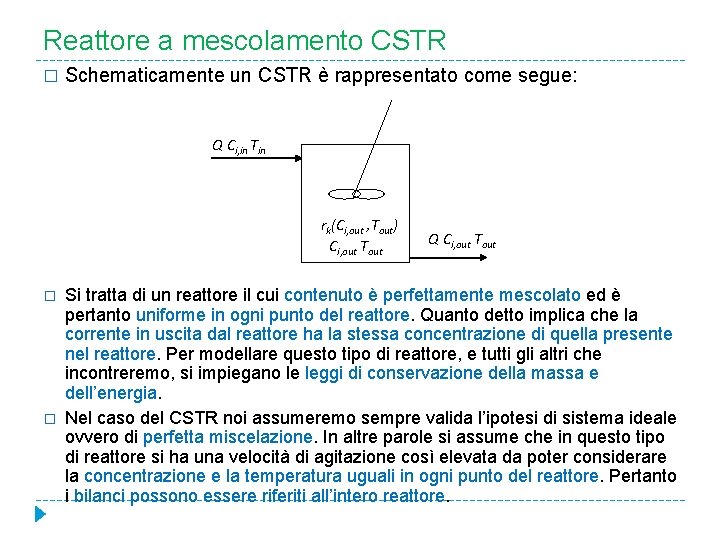
Reattore a mescolamento CSTR � Schematicamente un CSTR è rappresentato come segue: Q Ci, in Tin rk(Ci, out , Tout) Ci, out Tout � � Q Ci, out Tout Si tratta di un reattore il cui contenuto è perfettamente mescolato ed è pertanto uniforme in ogni punto del reattore. Quanto detto implica che la corrente in uscita dal reattore ha la stessa concentrazione di quella presente nel reattore. Per modellare questo tipo di reattore, e tutti gli altri che incontreremo, si impiegano le leggi di conservazione della massa e dell’energia. Nel caso del CSTR noi assumeremo sempre valida l’ipotesi di sistema ideale ovvero di perfetta miscelazione. In altre parole si assume che in questo tipo di reattore si ha una velocità di agitazione così elevata da poter considerare la concentrazione e la temperatura uguali in ogni punto del reattore. Pertanto i bilanci possono essere riferiti all’intero reattore.

CSTR isotermo in regime stazionario (1) � Per semplicità assumiamo, per il momento, che la temperatura è costante lungo il processo: � Se la temperatura è costante vuol dire che la temperatura in uscita del reattore, che ricordiamo essere uguale – per un CSTR – a quella presente nel reattore, coincide con quella in ingresso. � Per modellare un CSTR ideale ed isotermo bisogna quindi scrivere solo bilanci di materia: q. tà entrante = q. tà uscente + q. tà che scompare per reazione + q. tà accumulata =0

CSTR isotermo in regime stazionario (2) � Detta r(C) la velocità di reazione di un generico processo in condizioni isoterme (T= costante) il bilancio per un CSTR in condizioni stazionarie può essere scritto come segue: = Massa entrante per unità di tempo. Con il simbolo Q si è inteso indicare la portata volumetrica alimentata al reattore = Massa uscente per unità di tempo. = Massa reagita per unità di tempo. � Con il simbolo V si è inteso indicare il volume del fluido reagente contenuto nel reattore. Pertanto si ha: Il rapporto V/Q ha le dimensioni di un tempo e rappresenta il tempo di residenza del sistema. Ovvero esprime il tempo che (mediamente) il fluido trascorre nel reattore. Questo tempo lo indicheremo sempre con .

CSTR isotermo in regime stazionario (3) � L’equazione: descrive il bilancio di materia per un reattore continuo a perfetta miscelazione (CSTR) in condizioni stazionarie, temperatura costante (processo isotermo) e per un generico processo. � Il grado di conversione per una reazione può essere definito come segue: da cui: � Per com’è definita, x è una grandezza sempre positiva e 1, e rappresenta il grado d’avanzamento di una reazione. � Riferendosi ad un reagente si ha (non si è avuta reazione, la concentrazione del reagente in uscita dal reattore è uguale a quella in ingresso); (si è convertito tutto il reagente alimentato al reattore, in altre parole, si è avuto il massimo della conversione).

CSTR isotermo in regime stazionario (4) � In termini di grado di conversione, l’equazione di bilancio può essere riscritta come segue: � Nel caso di una reazione con cinetica del primo ordine si ha e quindi la funzione assume l’espressione: � Quindi l’equazione di bilancio essere scritta come segue: da cui: definiamo ora il numero adimensonale: che prende il nome di numero di Damköhler.

CSTR isotermo in regime stazionario (5) � La conversione ottenuta sarà quindi pari a: � Per una reazione di ordine qualsiasi il numero di Damköhler è definito come: � Attraverso il numero adimensionale di Damköhler (Da) sono confrontati due tempi caratteristici del sistema: il tempo di residenza ed il tempo di reazione . � È importante osservare che un problema reattoristico ha senso fin tanto che Da ha un valore prossimo ad uno. Infatti se Da è molto più grande di 1 allora il tempo di residenza è molto più grande del tempo caratteristico della reazione, e quindi la reazione è quasi esaurita o si è molto vicini all’equilibrio. In altre parole il reattore è sovradimensionato rispetto al processo che s’intende condurre. Al contrario se Da è molto minore di 1, il reattore risulta sottoutilizzato: occorre lasciare che la reazione vada ancora avanti se si vuole sfruttare la potenzialità del reattore.

Esercizio 1 � Scegliere quale tra le tre configurazioni reattoristiche è la più conveniente: 1) V=50 l, Q=2. 5 l/h, k=5. 5 h-1 2) V=1 l, Q=2. 5 l/h, k=5. 5 h-1 3) V=5 l, Q=150 l/h, k=5. 5 h-1 � In tutti e tre i casi proposti impiegare una cinetica del primo ordine (k. C). Confrontare le conversioni ottenute con le tre configurazioni reattoristiche. � Usando l’espressioni: � Otteniamo:

Esercizio 2 (1)

Esercizio 2 (2)

Cascata di CSTR (1) Una serie di reattori funziona meglio di un reattore unico a parità di condizioni (volume totale e portata) perché la reazione avviene a velocità diverse – e più alte – in funzione della concentrazione del reagente che si stabilisce in ciascun reattore, che è sempre più alta di quella del reattore finale. � In prima analisi, per semplicità, si considera la cascata di due soli reattori. Schematicamente si può rappresentare come segue: � C 0 C 1 C 2 � Si considera il caso di due reattori di volume uguale attraversati dalla stessa portata di fluido. L’uscita del primo reattore è l’ingresso del secondo. La reazione è la stessa nei due reattori ed è un processo isotermo del primo ordine.

Cascata di CSTR (2) � Detti ed i gradi di conversione riferiti alle rispettive concentrazioni in ingresso, calcolando le concentrazioni in uscita dai due reattori si ottiene: da cui: � Con le precedenti ipotesi si può affermare che il numero di Damköhler per i due reattori è uguale e che quindi, dato che lo è anche il grado di conversione, perciò x 1=x 2=x e quindi si ha: � L’analisi può estendersi ad n reattori uguali in serie, ottenendo:

Cascata di CSTR (3) � Inoltre, nelle ipotesi precedenti si dimostra che il grado di conversione della serie di n reattori è migliore di quello di un unico reattore con volume pari a quello della somma degli n reattori. Difatti si ha: e, introdotto (grado di conversione per l’intero sistema di n reattori) si ha: � Preso invece un reattore unico di volume pari alla somma dei volumi della serie di reattori, il corrispondente numero di Damköhler è legato a quello del singolo reattore della serie dalla ovvia relazione: � Si ha quindi, per il grado di conversione nel reattore unico, l’espressione:

Cascata di CSTR (4) � Non è difficile dimostrare che è sempre minore di . Ad esempio, si consideri il caso . Occorre far vedere che: e difatti, con facili calcoli si perviene all’espressione: che è sempre verificata. � L’equazione (*) ci consente di esprimere il grado di conversione della cascata di n CSTR uguali in funzione del grado di conversione del singolo reattore. Difatti: e quindi:

Esempio 1 � Vtot=1 l, Q=2. 5 l/h, k=5. 5 h-1 =0. 4 h, Da=2. 2, x=0. 6875 n=1: xn=x=0. 6875 � n=2: xn=1 -(1/(1+Da))2=0. 9023 � n=3: xn=1 -(1/(1+Da))3=0. 9694 � n=4: xn=1 -(1/(1+Da))4=0. 9904 � n=5: xn=1 -(1/(1+Da))5=0. 9970 � n=6: xn=1 -(1/(1+Da))6=0. 9990 � n=7: xn=1 -(1/(1+Da))7=0. 9997 � n=8: xn=1 -(1/(1+Da))8=0. 9999 �… � n=29: xn=1 -(1/(1+Da))29=1. 0000 �

CSTR isotermo in regime transitorio (1) � Scriviamo il bilancio di materia come al solito: q. tà entrante = q. tà uscente + q. tà che scompare per reazione + q. tà accumulata dove è il tempo dimensionale. Se il volume e la portata sono costanti, introduciamo come prima il tempo di residenza τ = V/Q ed inoltre definiamo il tempo adimensionale per scrivere: che si ottiene applicando la regola di derivazione delle funzione composte. Dalla definizione di tempo adimensionale: In generale, se la concentrazione in ingresso varia nel tempo, la definizione di grado di conversione va riscritta rispetto ad un valore costante di riferimento per la concentrazione. Questa procedura sarà adottata per il reattore non isotermo in regime transitorio.

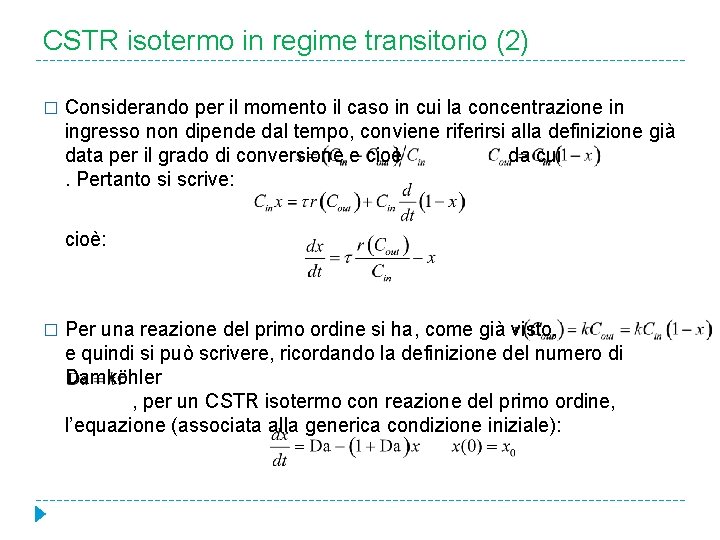
CSTR isotermo in regime transitorio (2) � Considerando per il momento il caso in cui la concentrazione in ingresso non dipende dal tempo, conviene riferirsi alla definizione già data per il grado di conversione e cioè da cui . Pertanto si scrive: cioè: � Per una reazione del primo ordine si ha, come già visto, e quindi si può scrivere, ricordando la definizione del numero di Damköhler , per un CSTR isotermo con reazione del primo ordine, l’equazione (associata alla generica condizione iniziale):

CSTR isotermo in regime transitorio (3) � Si scrive immediatamente la soluzione analitica: in cui si riconosce a fattor comune la soluzione asintotica per t ; cioè, posto: si scrive: Si vede che la soluzione è così espressa come la soluzione asintotica moltiplicata per 1+ il transitorio. CSTR isotermo, reazione del primo ordine: grado di conversione in funzione del tempo al variare di Da.

CSTR isotermo in regime transitorio (4) � Nel caso di reazione globale isoterma del secondo ordine si ha , da cui: e cioè:

CSTR non isotermo in regime stazionario (1) Se non è più possibile trascurare le variazioni di temperatura per effetto della reazione l’equazione di bilancio di massa non è più sufficiente da sola a modellare un CSTR ideale. � Infatti ricordando che la velocità di reazione dipende dalla concentrazione e dalla temperatura la dovrebbe essere riscritta come segue: � = 0 (poiché l’energia Quando il sistema non può essere considerato isotermo occorre totale si conserva) = 0 (sistema affiancare al bilancio di materia anche un bilancio d’energia: stazionario) q. tà entrante = q. tà uscente + q. tà distrutta + q. tà accumulata � Nelle quantità entranti e uscenti sono comprese sia le quantità legate alle correnti entranti ed uscenti, sia l’energia scambiata nel modo calore attraverso i confini del sistema, sia il lavoro meccanico. Se il lavoro meccanico è uguale a zero ed il sistema è adiabatico, il bilancio d’energia può essere scritto come segue: �

CSTR non isotermo in regime stazionario (2) � Dove è la portata entalpica entrante, data dal prodotto di portata massica entrante per entalpia specifica per unità di massa della miscela entrante. Per miscele ideali l’entalpia della miscela si esprime come: e dove è la portata entalpica uscente, data dal prodotto di portata massica uscente (uguale a quella entrante per regime stazionario) per entalpia specifica per unità di massa della miscela uscente, espressa come: dove è la frazione di massa della specie i (massa della specie i divisa per la massa totale). � In termini specifici, dato che la portata massica è uguale fra ingresso e uscita, si ha:

CSTR non isotermo in regime stazionario (3) � L’entalpia specifica per unità di massa della specie i si scrive: in cui è l’entalpia di formazione per unità di massa della specie i valutata alla temperatura di riferimento e è il calore specifico a pressione costante per unità di massa della specie i. Il calore specifico è funzione delle temperatura. Sostituendo nelle espressioni dell’entalpia di ingresso e di uscita della miscela si ha:

CSTR non isotermo in regime stazionario (4) � Per semplicità si supponga che i valori medi integrali dei calori specifici a pressione costante siano costanti ed uguali per tutte le specie. In questa ipotesi, sostituendo nel bilancio di energia si ottiene: da cui: ossia: dove: è l’energia termica liberata per effetto delle reazioni chimiche avvengono nel reattore ed è diversa da zero se la composizione della miscela cambia tra ingresso e uscita per effetto della reazione chimica e se vi è una variazione netta non nulla nella entalpia di formazione tra miscela di reagenti e miscela di prodotti.

CSTR non isotermo in regime stazionario (5) � Si definisce entalpia di reazione e si indica con la variazione di entalpia fra reagenti e prodotti di una reazione chimica, per conversione completa di una miscela stechiometrica di reagenti puri che avviene a temperatura e pressione costanti ovvero riportate allo stato standard. L’entalpia di reazione si calcola facilmente dalle entalpie di formazione dei reagenti e dei prodotti ed è tabellata per le reazioni più comuni con riferimento ad una mole di uno dei reagenti.

CSTR non isotermo in regime stazionario (6) � Nel caso di una sola reazione chimica che avviene in un reattore in flusso in regime stazionario, l’energia termica liberata sarà quindi uguale all’entalpia di reazione (riferita ad una mole di reagente) moltiplicata per le moli di reagente convertite, cioè per la concentrazione di reagente nella corrente in ingresso, , moltiplicata per il grado di conversione x raggiunto, cambiata di segno. In queste ipotesi, e sfruttando la definizione del grado di conversione, il bilancio d’energia, per unità di volume, può essere scritto come segue: dove si ricorda che si è supposto il sistema adiabatico e senza scambi di energia nel modo lavoro attraverso i confini. La quantità: rappresenta il massimo incremento di temperatura ottenibile per effetto della reazione chimica per conversione completa (Delta T adiabatico).

CSTR non isotermo in regime stazionario (7) � In corrispondenza di un valore x del grado di conversione si avrà quindi: ovvero, posto � Detta la velocità di reazione in funzione di composizione e temperatura, la legge di Arrhenius si esprime come: e, utilizzando (*) si ha: , si scrive:

CSTR non isotermo in regime stazionario (8) � Sostituendo l’espressione di k (costante di velocità di reazione) nella per una reazione del primo ordine, cioè con , si ottiene: che si trasforma facilmente, introdotto il nuovo parametro adimensionale , in: che è infine una sola equazione nella x. In questa espressione si riconosce che, per ossia per reazione in cui non vi è conversione di energia potenziale chimica in energia termica (e quindi, nelle ipotesi fatte, reazione isoterma) il secondo esponenziale è =1. Pertanto l’espressione si riduce a: che restituisce quella del reattore isotermo.

CSTR non isotermo in regime stazionario (9) � Il prodotto: è di fatto la costante di velocità di reazione k introdotta per la reazione isoterma del primo ordine, da cui la definizione adottata per il numero di Damköhler, , in questo caso, coerente con quella del reattore isotermo. � l’espressione che fornisce il grado di conversione x in regime stazionario è: � Nelle ipotesi fatte, esiste una relazione lineare fra la temperatura ed il grado di conversione. Se definiamo la temperatura adimensionale come: ed assumiamo quale la temperatura in ingresso al reattore, si ricava:

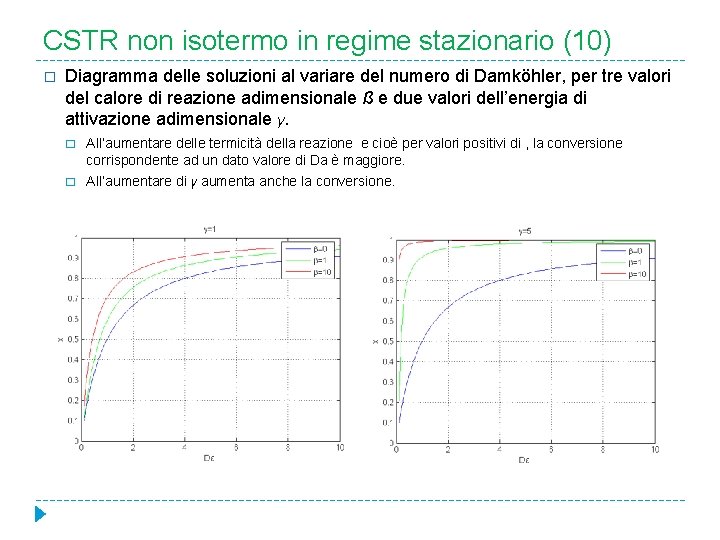
CSTR non isotermo in regime stazionario (10) � Diagramma delle soluzioni al variare del numero di Damköhler, per tre valori del calore di reazione adimensionale ß e due valori dell’energia di attivazione adimensionale γ. � All’aumentare delle termicità della reazione e cioè per valori positivi di , la conversione corrispondente ad un dato valore di Da è maggiore. � All’aumentare di γ aumenta anche la conversione.

CSTR non isotermo in regime transitorio caso non adiabatico (1) � Analogamente a quanto fatto per il CSTR ideale in condizioni isoterme, scriviamo l’equazione di bilancio di materia per un CSTR non isotermo non stazionario con singola reazione: � Se il volume e la portata sono costanti, introduciamo come prima il tempo di residenza ed inoltre definiamo il tempo adimensionale per scrivere: � In questo caso (regime transitorio), in cui i valori in ingresso di temperatura e concentrazione possono variare nel tempo, è opportuno introdurre valori arbitrari per le grandezze di riferimento. Definiamo quindi da cui e, in particolare, . La (*) si può scrivere quindi: cioè:

CSTR non isotermo in regime transitorio caso non adiabatico (2) � Per reazione del primo ordine si ha: e quindi: � Se la reazione segue la legge di Arrhenius per la dipendenza dalla temperatura, si ha:

CSTR non isotermo in regime transitorio caso non adiabatico (3) � L’equazione di bilancio di energia si scrive come: In questa equazione U è il coefficiente di scambio termico (energia scambiata per unità di superficie, di tempo e per grado Kelvin), supposto costante, S è l’area della superficie esterna del reattore, è la temperatura esterna al reattore (non necessariamente uguale alla temperatura di ingresso . Il termine rappresenta la quantità di energia che “scompare” nell’unità di tempo per effetto della reazione chimica ed è ovviamente proporzionale alla quantità di materia reagente che “scompare” nell’unità di tempo. Se il volume V, la portata Q, la densità ρ ed il calore specifico sono costanti, introduciamo come prima il tempo di residenza ed inoltre definiamo il tempo adimensionale per scrivere:

CSTR non isotermo in regime transitorio caso non adiabatico (4) � Definiamo l’entalpia di reazione adimensionale: e la temperatura adimensionale, come prima: dove al denominatore con si fa riferimento al valore massimo dell’incremento di temperatura raggiungibile nel reattore, in condizioni adiabatiche e per conversione totale a partire da una concentrazione di reagente uguale a quella di riferimento. � Esplicitando si ha: e anche, ovviamente:

CSTR non isotermo in regime transitorio caso non adiabatico (5) � Sostituendo nel’equazione di bilancio si ha: � Si considera qui il caso di reazione del primo ordine, in cui , da cui: e, dividendo tutto per e moltiplicando tutto per : Sia infine (coefficiente di scambio termico adimensionale) e riordiniamo per scrivere l’equazione di bilancio dell’energia in forma:

CSTR non isotermo in regime transitorio caso non adiabatico (6) � Se la reazione segue la legge di Arrhenius per la dipendenza dalla temperatura, si ha: dove: e abbiamo definito anche:

CSTR non isotermo in regime transitorio caso non adiabatico (7) � Riportiamo l’equazione di bilancio di materia e quindi le due equazioni si scrivono come: � Il parametro dipende dal tempo di residenza e pertanto, se il numero di Damkohler varia per effetto della variazione del tempo di residenza (portata al reattore), varierà anch’esso proporzionalmente. Allora conviene esplicitare la dipendenza da di ponendo: con , da cui la nuova espressione per il sistema di equazioni: associate alle condizioni iniziali:

CSTR non isotermo in regime transitorio caso adiabatico (1) � Se il reattore è adiabatico (niente perdite attraverso le pareti) si ha =0 e quindi le due equazioni si scrivono come: � Esse possono essere combinate per dare: � Si faccia l’ipotesi di lavoro che esista qualche soluzione tale che . In questo caso e perciò, se (condizioni in ingresso) e (condizioni iniziali) l’equazione: rappresenta l’equazione di bilancio transitorio di materia, associata alla generica condizione iniziale .

CSTR non isotermo in regime transitorio caso adiabatico (2) � Essa è sufficiente a determinare, da sola, lo stato del reattore, poiché appunto . Si noti che, per , ossia reazione isoterma, l’equazione restituisce quella scritta, per l’appunto, per il transitorio di un CSTR isotermo:

Comportamento stazionario non adiabatico � Ponendo nelle (*) si ottiene il modello per il caso stazionario non adiabatico:

Reattore discontinuo BATCH

BATCH isotermo a volume costante (1) � Si tratta di un reattore non continuo, BATCH, per il quale non c’è nessuna portata entrante e nessuna portata uscente. Schematicamente è rappresentato come segue: � In questo tipo di operazioni, i reagenti sono caricati all’interno del reattore dove sono continuamente mescolati e lasciati reagire per un tempo necessario ad ottenere una data conversione. La composizione e la temperatura (caso non isotermo) cambiano con il tempo all’interno del reattore e, per l’ipotesi di perfetta miscelazione, sono uguali in ogni punto del reattore. Non ci sono quindi variabili spaziali e le grandezze dipenderanno soltanto dal tempo.

BATCH isotermo a volume costante (2) � Assumiamo per semplicità che il processo che si vuole modellare possa essere considerato isotermo (temperatura costante). In questo caso le concentrazioni sono le incognite, che sono rappresentate come funzioni del tempo. � Per determinare l’andamento delle concentrazioni all’interno del reattore nel tempo bisogna scrivere un bilancio di materia. Per ricavare le equazioni che modellano un reattore isotermo di tipo BATCH effettuiamo un bilancio tra un generico tempo ed un tempo . Al tempo il reagente presente nel reattore è: � Al tempo � La quantità di reagente presente al tempo è diversa da quella presente nel reattore al tempo perché in questo intervallo di tempo parte del reagente si è consumato per effetto della reazione. il reagente presente nel reattore sarà:

BATCH isotermo a volume costante (3) � Detta r la velocità di reazione, espressa in moli per unità di volume e di tempo, funzione della concentrazione del reagente, la quantità di reagente consumato per effetto della reazione nell’intervallo di tempo è: � Raggruppando i termini, l’equazione di bilancio per un reattore BATCH isotermo può essere espressa come segue: � Il termine si espande in serie di Taylor arrestata al primo termine, pertanto il bilancio (*) può essere scritto come segue:

BATCH isotermo a volume costante (4) � L’equazione di bilancio di materia per un reattore BATCH è espressa quindi da un’equazione differenziale ordinaria del primo ordine. Per chiudere il problema bisogna, pertanto, specificare anche una condizione iniziale. Questa può essere rappresentata dal valore della concentrazione all’interno del reattore al tempo zero, in altre parole al tempo al quale ha inizio il processo. Se si introduce il tempo adimensionale , l’equazione diventa: � In termini di grado di conversione essere riscritta come segue: , l’equazione di bilancio può

BATCH isotermo a volume costante (5) � L’equazioni di bilancio possono essere impiegate per ricavare il tempo necessario per ottenere un dato grado di conversione e viceversa. Esse sono “a variabili separabili” e pertanto si integrano immediatamente: � Si ponga t 0=0 e si prenda in esame il caso di una reazione del primo ordine: � Allora, se si sceglie � Dalla (*) si ha: , l’equazione di bilancio di materia diventa:

BATCH isotermo a volume costante (6) � Se introduciamo il numero di Damköhler all’espressione: perveniamo � Si può osservare come per una reazione del primo ordine il risultato non dipenda dalla concentrazione iniziale.

Caso di reazione del ordine n≠ 1 � Nel caso che la reazione n≠ 1) del tipo: sia irreversibile e di ordine n (con si ha: � L’equazione di bilancio è quindi: � L’equazione costitutiva del reattore batch si ricava quindi così: dove:

Legge di stato dei gas perfetti � Un gas ideale rispetta la legge dei gas perfetti: dove: p – il pressione del gas V – il volume occupato dal gas n – le moli del gas R – la costante universale dei gas (nel SI R=8, 314472 J/(mol K)) T – la temperatura espressa in Kelvin � La mole è definita come la quantità di sostanza che contiene un numero di unità interagenti (atomi, molecole, ioni, radicali, elettroni, fotoni, ) pari al numero degli atomi presenti in 12 grammi di carbonio-12 (ed è pari a 6, 02214179(30) 1023 - numero di Avogadro)

BATCH isotermo a volume variabile (1) � Consideriamo ora il caso del volume variabile. Dato che il volume varia per effetto della reazione bisogna, nel bilancio, tenere in conto anche la dipendenza del volume dal tempo, e pertanto: e quindi: � L’equazione (*) è stata scritta nell’ipotesi di temperatura costante e quindi la variazione di volume è legata esclusivamente alla variazione della concentrazione che avviene all’interno del reattore per effetto della reazione: . Per il teorema sulla derivazione delle funzioni composte si ha: Il termine scritto fra parentesi nell’equazione (**) rappresenta il coefficiente di dilatazione cubica del sistema. Questo coefficiente esprime appunto come varia il volume del sistema al variare della concentrazione. L’equazione (**) può essere scritta in una forma più semplice, se si introduce la seguente variabile:

BATCH isotermo a volume variabile (2) � Derivando rispetto al tempo i membri della (***) ed introducendo il tempo adimensionale, si ha: e pertanto la (*) può essere riscritta come segue: � Questa espressione è molto comoda nel caso che si disponga di un’equazione costitutiva che descrive le variazioni del volume con la conversione del sistema: in tal caso si può ottenere un’equazione nella sola incognita . Se il volume varia linearmente con la conversione, cioè la (*) diviene:

BATCH isotermo a volume variabile (3) � In combinazione con l’espressione: si ricava il legame fra ed x: � Per una reazione del primo ordine, si ha: � Poniamo e riconosciamo che e, per il problema di progetto: , da cui:

BATCH isotermo a volume variabile (4) � Quest’equazione, ancora una volta, consente di determinare il tempo necessario per ottenere un dato grado di conversione o viceversa. Nell’esempio, per una reazione del primo ordine: e, ricordando che :

Esercizio 1 � Determinare il tempo di reazione tf necessario per avere una conversione xf desiderata nel caso che la reazione gassosa sia irreversibile e di ordine 1 (cioè ) ed avvenga in un reattore BATCH a volume variabile. � Determiniamo innanzitutto il valore di nell’espressione � Se tutto il componente A reagisce per formare B, e quindi per x=1, avremo il raddoppio del volume dei gas (da una mole se ne sono formate due) e quindi: � Applichiamo la formula: � Se xf=0. 5 tf=0. 6931, xf=0. 99 tf= 4. 6052, xf=1. 0 tf= .

BATCH non isotermo (1) � Se non è più possibile trascurare le variazioni di temperatura per effetto della reazione, l’equazione di bilancio di materia non sarà più sufficiente da sola a modellare un reattore BATCH � Scriviamo l’equazione non stazionaria di bilancio di materia per un BATCH non isotermo con singola reazione: � Se il volume è costante: � Ricordando che il grado di conversione è definito come da cui si scrive: cioè:

BATCH non isotermo (2) � Per una reazione del primo ordine si ha, come già visto: e quindi si può scrivere: � Se la reazione segue la legge di Arrhenius per la dipendenza dalla temperatura, si ha:

BATCH non isotermo (3) � Quando il sistema non può essere considerato isotermo occorre affiancare al bilancio di materia anche un bilancio d’energia. Vale sempre, come per ogni grandezza conservata, la relazione: quantità entrante = quantità uscente + quantità che scompare per reazione + quantità accumulata che nel caso in esame si scrive come: dove: QP - (quantità uscente) è l’energia che il sistema perde attraverso le pareti del reattore per raffreddamento ad opera dell’ambiente - è la quantità che scompare per reazione, cioè la quantità prodotta presa con il segno meno (ricordiamo che reazioni esotermiche hanno negativo) - è la quantità accumulata, dove cp è il calore specifico a pressione costante su base massica, mentre è il tempo dimensionale. � La perdita QP si esprime come:

BATCH non isotermo (4) � Per rendere adimensionale l’equazione definiamo: e la temperatura adimensionale: dove è la massima temperatura raggiungibile dal reattore, in condizioni adiabatiche e per conversione unitaria (quindi varia tra zero e uno). � Definiamo il tempo adimensionale � Sostituendo in: si ha: posto : .

BATCH non isotermo (5) ; . � Si considera qui il caso di reazione del primo ordine, in cui e supponiamo che la dipendenza dalla temperatura sia di tipo Arrhenius, cioè: che diventa: che conviene mettere nella forma dove � Si scelga infine quale tempo di riferimento . Riordinando, l’equazione di bilancio dell’energia prende la forma: � L’equazione di bilancio di materia è: � Ad esse sono associate le condizioni iniziali .

BATCH non isotermo caso adiabatico � Se il reattore è adiabatico (niente perdite attraverso le pareti) si ha pertanto l’equazione di bilancio dell’energia si riduce a: e � L’equazione di bilancio di materia è: � Si vede che i secondi membri sono uguali e perciò, se allora , quindi il reattore è compiutamente descritto dalla sola equazione differenziale: che rappresenta l’equazione di bilancio di materia, associata alla condizione iniziale . Essa è sufficiente a determinare, da sola, lo stato del reattore. Si noti che, per , ossia reazione isoterma, l’equazione restituisce quella scritta, per l’appunto, per il funzionamento di un reattore BATCH isotermo:

Esempio: BATCH non isotermo non adiabatico (1) � Il caso non adiabatico, con reazione del primo ordine e legge di Arrhenius per la dipendenza dalla temperatura della velocità di reazione, è retto dalle seguenti equazioni e relative condizioni iniziali:

Esempio: BATCH non isotermo non adiabatico (2) � Per risolvere il problema numericamente si può applicare un metodo di Eulero. In forma esplicita, il metodo genera le seguenti formule: � Il metodo di Eulero implicito produce invece le seguenti equazioni: cioè: Tale sistema va risolto ad ogni passo di tempo con un metodo iterativo, tipicamente Newton-Raphson.

Esempio: BATCH non isotermo non adiabatico (3) � Ai fini di una migliore stabilità, senza dover risolvere un sistema non lineare, conviene ricorrere ad un metodo di Eulero semi-implicito, ossia: (trattiamo in implicito la parte lineare e in esplicito termine non lineare) da cui, posto :

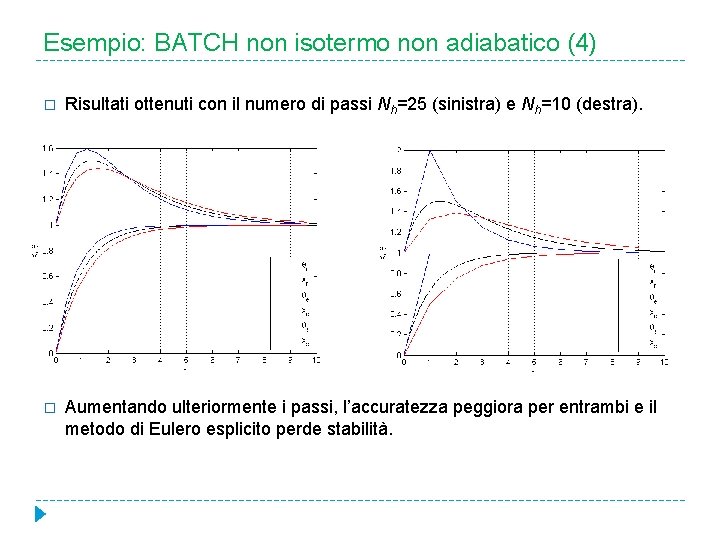
Esempio: BATCH non isotermo non adiabatico (4) � Risultati ottenuti con il numero di passi Nh=25 (sinistra) e Nh=10 (destra). � Aumentando ulteriormente i passi, l’accuratezza peggiora per entrambi e il metodo di Eulero esplicito perde stabilità.

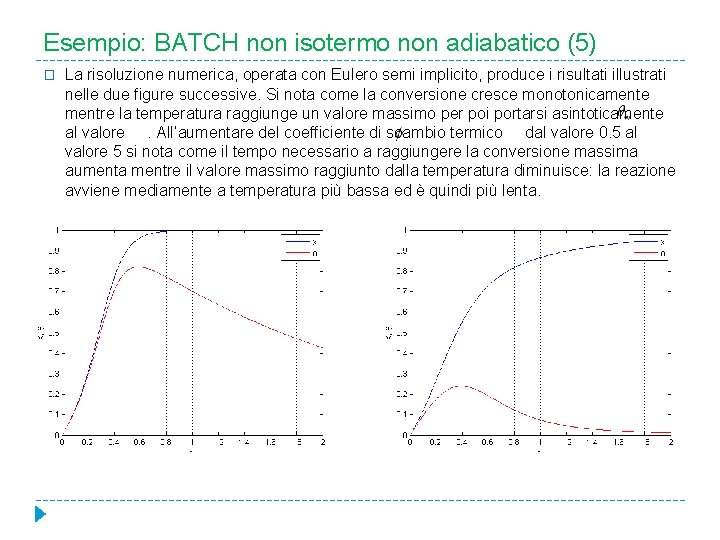
Esempio: BATCH non isotermo non adiabatico (5) � La risoluzione numerica, operata con Eulero semi implicito, produce i risultati illustrati nelle due figure successive. Si nota come la conversione cresce monotonicamente mentre la temperatura raggiunge un valore massimo per poi portarsi asintoticamente al valore . All’aumentare del coefficiente di scambio termico dal valore 0. 5 al valore 5 si nota come il tempo necessario a raggiungere la conversione massima aumenta mentre il valore massimo raggiunto dalla temperatura diminuisce: la reazione avviene mediamente a temperatura più bassa ed è quindi più lenta.

Resa e selettività � Il rendimento (o resa) è il rapporto tra la quantità di prodotto formato e quella di reagente iniziale consumato: � Si definisce selettività rispetto al reagente il rapporto tra gli equivalenti di prodotto formato e quella di reagente consumato (prodotto totale formato): � Per esempio per la rete di reazioni: la selettività rispetto C è:

Esempio 1 � Si immagina che in un reattore avvengano le seguenti due reazioni del primo ordine: � Si suppone che le costanti di velocità delle due reazioni dipendano dalla temperatura secondo la legge di Arrhenius: � La selettività rispetto B è:

Esempio 2

BATCH non isotermo, due reazioni in parallelo (1) � Si immagina che in un reattore avvengano le seguenti due reazioni del primo ordine: � Si suppone che le costanti di velocità delle due reazioni dipendano dalla temperatura secondo la legge di Arrhenius: � Si devono perciò scrivere tre equazioni di bilancio, una per la specie A una per la specie B e una per la specie C. Per la specie A l’equazione di bilancio contiene due termini di generazione (consumo): � Se le reazioni sono del primo ordine, avremo:

BATCH non isotermo, due reazioni in parallelo (2) � Per la specie B e per la specie C il termine di generazione è uno solo: � Occorre affiancare ai bilanci di materia anche un bilancio d’energia, che in questo caso tiene conto del contributo di entrambe le reazioni: dove: Q - (quantità uscente) è l’energia che esce dal sistema attraverso le pareti del reattore per raffreddamento ad opera dell’ambiente - è la quantità che scompare per reazione - è la quantità accumulata, dove cp è il calore specifico a pressione costante su base massica, mentre è il tempo dimensionale

BATCH non isotermo, due reazioni in parallelo (3) � Conviene scrivere il sistema di quattro equazioni come segue: con le relative condizioni iniziali: � Si nota come le equazioni di bilancio per i prodotti B e C siano disaccoppiate dalle equazioni di bilancio per il reagente A e per l’energia. Si può in linea di principio perciò procedere con la risoluzione accoppiata di queste ultime due equazioni e risolvere poi le equazioni per i prodotti addirittura una per una separatamente una volta note la concentrazione di A e la temperatura nel tempo.

BATCH non isotermo, due reazioni in parallelo (4) , � Introduciamo le frazioni molari: la temperatura adimensionale: � Prendiamo come tempo di riferimento e introduciamo il parametro . Consideriamo per semplicità al momento solo reazioni equimolari, per cui . Si ha pertanto , e , con . Inoltre si ha . Definiamo i seguenti parametri adimensionali: � Sostituendo nelle equazioni di bilancio si ottiene:

BATCH non isotermo, due reazioni in parallelo (5) � Il sistema insieme con le condizioni iniziali: si può risolvere con un metodo numerico per problemi di valori iniziali. Si nota che per valori diversi delle costanti di velocità di reazione il reagente A ovviamente si trasformerà in proporzioni disuguali in B e C. La dipendenza dalla temperatura si può sfruttare per ottenere una selezione fra B e C.

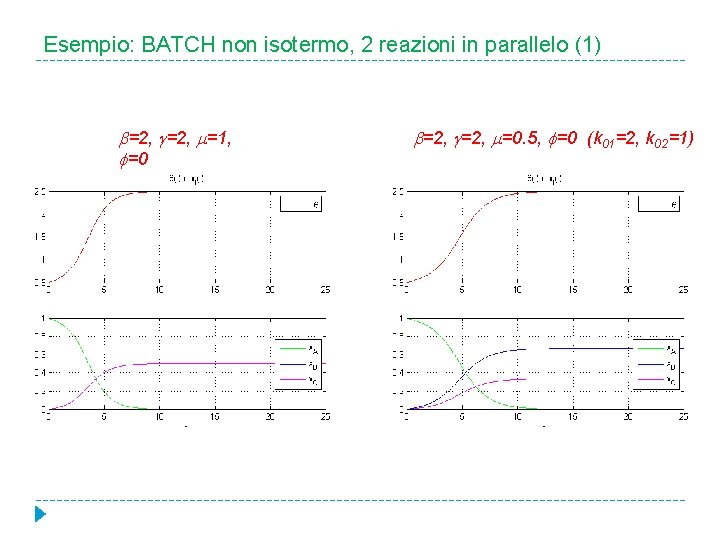
Esempio: BATCH non isotermo, 2 reazioni in parallelo (1) =2, =1, =0 =2, =0. 5, =0 (k 01=2, k 02=1)

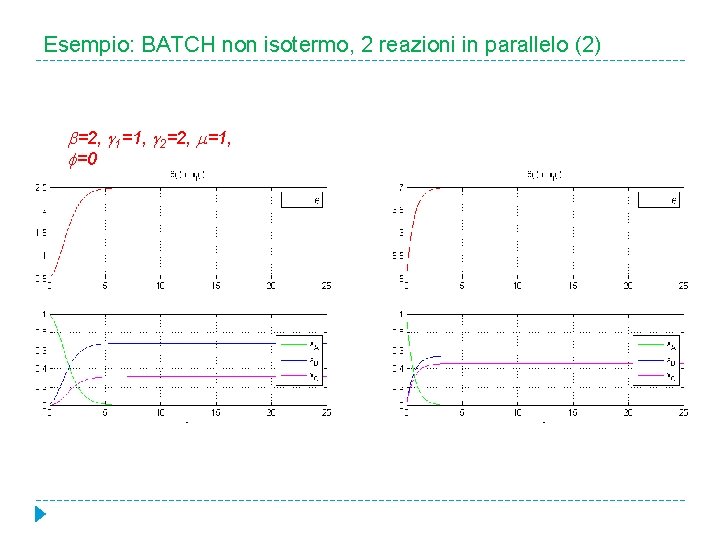
Esempio: BATCH non isotermo, 2 reazioni in parallelo (2) =2, 1=1, 2=2, =1, =0

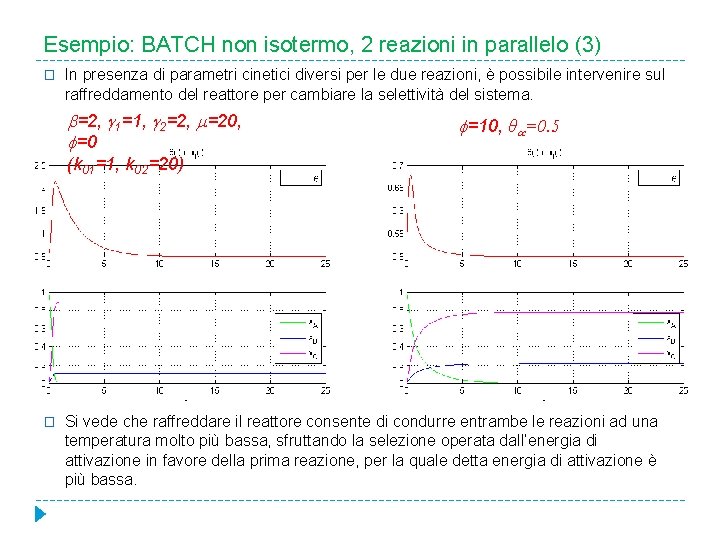
Esempio: BATCH non isotermo, 2 reazioni in parallelo (3) � In presenza di parametri cinetici diversi per le due reazioni, è possibile intervenire sul raffreddamento del reattore per cambiare la selettività del sistema. =2, 1=1, 2=2, =20, =0 =10, θ =0. 5 (k 01=1, k 02=20) � Si vede che raffreddare il reattore consente di condurre entrambe le reazioni ad una temperatura molto più bassa, sfruttando la selezione operata dall’energia di attivazione in favore della prima reazione, per la quale detta energia di attivazione è più bassa.

BATCH non isotermo, due reazioni in serie (1) � Si immagina che in un reattore avvengano le seguenti due reazioni del primo ordine: � Si suppone che le costanti di velocità delle due reazioni dipendano dalla temperatura secondo la legge di Arrhenius: � Si devono perciò scrivere due equazioni di bilancio, una per la specie A ed un’altra per la specie B (la specie C si può ricavare da una relazione algebrica). Per la specie A l’equazione di bilancio è: � Per la specie B il termine di generazione si compone di due quantità: quella che rappresenta la generazione a partire da A secondo la prima reazione, più quella che rappresenta la scomparsa per effetto della seconda reazione:

BATCH non isotermo, due reazioni in serie (2) � Occorre affiancare ai bilanci di materia anche un bilancio d’energia, che in questo caso tiene conto del contributo di entrambe le reazioni: � Conviene scrivere il sistema di tre equazioni come segue: con le relative condizioni iniziali: � La concentrazione della specie C si potrà calcolare in un secondo momento, note che siano T e CB , dalla equazione (disaccoppiata dalle altre):

BATCH non isotermo, due reazioni in serie (3) , � Introduciamo le frazioni molari: la temperatura adimensionale: � Prendiamo come tempo di riferimento e introduciamo il parametro . Consideriamo per semplicità al momento solo reazioni equimolari, per cui . Si ha pertanto , e , con . Inoltre si ha . Definiamo i seguenti parametri adimensionali: � Sostituendo nelle equazioni di bilancio si ottiene:

BATCH non isotermo, due reazioni in serie (4) � Il sistema insieme con le condizioni iniziali: si può risolvere con un metodo numerico per problemi di valori iniziali.

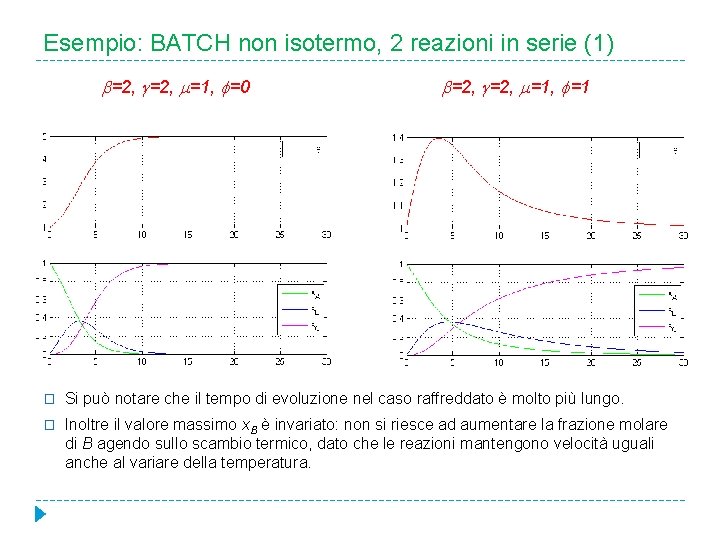
Esempio: BATCH non isotermo, 2 reazioni in serie (1) =2, =1, =0 =2, =1, =1 � Si può notare che il tempo di evoluzione nel caso raffreddato è molto più lungo. � Inoltre il valore massimo x. B è invariato: non si riesce ad aumentare la frazione molare di B agendo sullo scambio termico, dato che le reazioni mantengono velocità uguali anche al variare della temperatura.

Esempio: BATCH non isotermo, 2 reazioni in serie (2) 1=10, 2=0, =5, =0. 1, =0 � � 1=10, 2=0, =5, =0. 1, =0. 3 Il tempo di evoluzione nel caso raffreddato è solo lievemente più lungo; ciò dovuto alla termicità elevata della prima reazione e quindi alla elevata velocità di reazione che si mantiene tale anche per reattore raffreddato. Il valore massimo di x. B non è cambiato, però è più agevole l’esercizio del reattore per raccogliere prodotto ad alto contenuto di B, dato che il raffreddamento “congela” la composizione in corrispondenza del valore massimo raggiunto da x. B.

Reattore con flusso a pistone PFR

Reattore con flusso a pistone (PFR) � Questo tipo di reattore è caratterizzato dal fatto che il moto dei fluidi attraverso il reattore è ordinato in modo tale che nessun elemento di fluido si mescola o si sovrappone con un elemento di fluido che sta avanti o indietro. In questi reattori si ha una completa miscelazione solo nelle direzioni ortogonali al moto ma non in quella del moto stesso. Da queste considerazioni scaturisce l’osservazione che in un reattore con flusso a pistone (PFR) tutti gli elementi di fluido hanno la stessa velocità e quindi lo stesso tempo di permanenza. � Per studiare questo tipo di reattori si fanno spesso le seguenti ipotesi: � � Le grandezze dipendono da una sola coordinata spaziale. Si trascurano i fenomeni di diffusione e conduzione termica lungo l’asse del reattore (direzione del moto).

Flusso a pistone con dispersione � Consideriamo il flusso a pistone di un fluido a cui venga sovrapposto un certo grado di retromiscelazione o intermiscelazione, la cui grandezza sia indipendente dalla posizione nel recipiente. Questa condizione comporta che non si hanno zone stagnanti o fenomeni notevoli di by-pass o di cortocirculazione; questo caso prende nome di modello di flusso a pistone disperso o modello di dispersione.

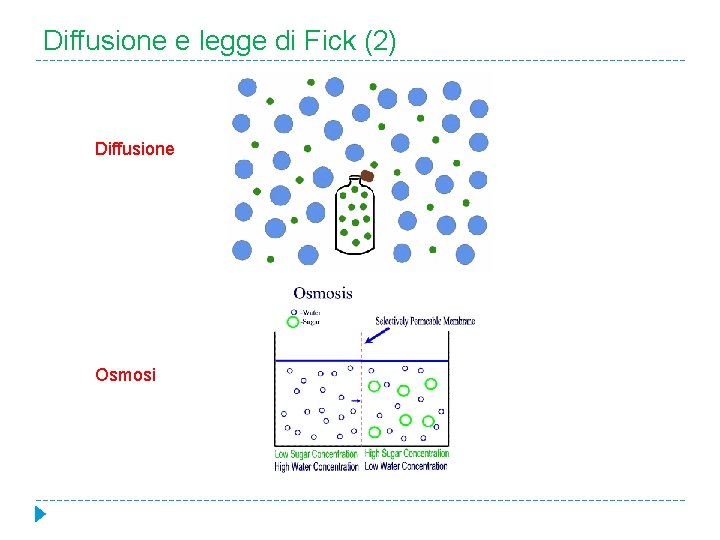
Diffusione e legge di Fick (1) � Poiché il processo di mescolamento comporta un ridistribuzione della materia e poiché questo si ripete un gran numero di volte durante il moto del fluido attraverso il recipiente, possiamo considerare che questi disturbi siano di tipo statistico, in un certo senso come nel caso della diffusione molecolare. Per quest’ultimo fenomeno , l’equazione differenziale nella direzione x è data dalla seconda legge di Fick: in cui D, coefficiente di diffusione molecolare, è il solo parametro che caratteriza il processo. In modo analogo possiamo considerare che tutti i contributi alla retromiscelazione del fluido che si muove nella direzione x possano essere descritti da una espressione simile, in cui il parametro D, che prende nome di coefficiente di dispersione longitudinale o assiale, caratterizza da solo il grado di retromiscelazione durante il flusso. (prima legge di Fick: , dove J è flusso lungo x).

Diffusione e legge di Fick (2) Diffusione Osmosi

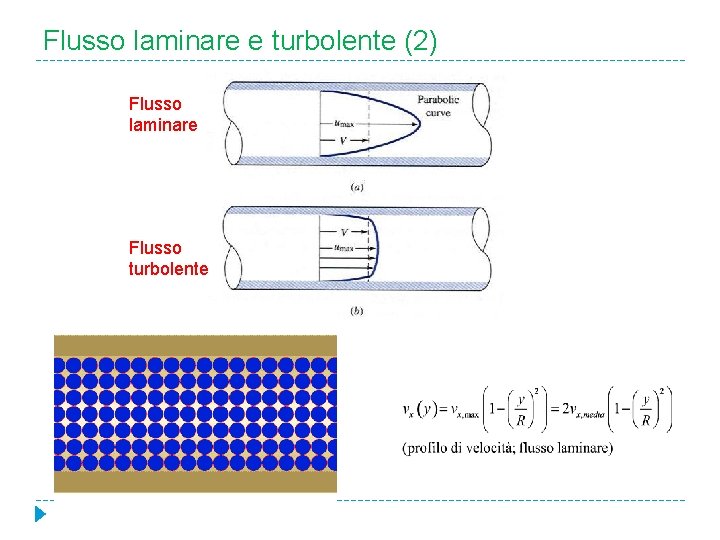
Flusso laminare e turbolente (1) � Numero di Reynolds: dove U – la velocità del fluido, - la viscosità dinamica, - la densità del fluido, L – diametro del tubo. � Flusso turbolente per Re≥ 3000.

Flusso laminare e turbolente (2) Flusso laminare Flusso turbolente

PRF isotermo in regime stazionario (1) � Indicando con z la distanza dall’imbocco del reattore, vogliamo determinare la funzione C(z). Il sistema di riferimento per cui scriveremo il bilancio sarà caratterizzato da un intervallo differenziale dz mentre per il tempo di osservazione possiamo considerare un intervallo finito ( t). z z+dz z � Detta Q la portata volumetrica in alimentazione al sistema, allora Q t rappresenta il volume entrato nel sistema attraverso la sezione S del reattore nell’intervallo di tempo t. � QC(z) t rappresenta la quantità della specie che si sta bilanciando (in moli) entrante nel sistema attraverso la sezione di ingresso nell’intervallo di tempo t, per effetto del moto complessivo del fluido attraverso il reattore (termine convettivo). Queste moli in parte reagiscono (e quindi scompaiono) ed in parte escono dal sistema. Le moli uscenti per convezione sono QC(z+dz) t mentre quelle che scompaiono per reazione nell’intervallo di tempo considerato sono pari a .

PRF isotermo in regime stazionario (2) � Non facciamo ipotesi sulla trascurabilità della diffusione assiale e procediamo a ricavare l’equazione completa. Il flusso di materia, anche se il fluido fosse fermo, non sarebbe nullo, per effetto della diffusione molecolare (legge di Fick). Il flusso diffusivo, per unità di superficie e di tempo, è proporzionale al gradiente di concentrazione. � Detto D il coefficiente di diffusione, il contributo entrante nel sistema in corrispondenza dell’ascissa z nel tempo t è pari a mentre il contributo uscente in corrispondenza dell’ascissa è pari a . � Raggruppando i termini si ottiene la seguente equazione di bilancio: Moli entranti per convenzion e Moli entranti per diffusione Moli uscenti per convezione Moli uscenti per diffusione Moli che scompaiono per reazione

PRF isotermo in regime stazionario (3) � Dividendo tutto per t ed espandendo in serie di Taylor termini uscenti e troncando ai termini del primo ordine: e sostituendo nel (*) si ha: si ottiene il seguente bilancio:

PFR isotermo in regime stazionario (4) � Per valutare l’importanza relativa dei tre termini dell’equazione di bilancio è opportuno operare una adimensionalizzazione. Prendiamo una lunghezza caratteristica zc, ed una concentrazione caratteristica Cc, per esempio C 0. Definiamo quindi le seguenti grandezze adimensionali: da cui: e inoltre:

PFR isotermo in regime stazionario (5) � Sostituendo nell’equazione di bilancio si ha: � Cioè, con qualche manipolazione: � Una possibile scelta per la lunghezza di riferimento potrebbe essere ad esempio: in modo che:

PFR isotermo in regime stazionario (6) � In questo caso si avrebbe: che si può scrivere come: dove il numero di Péclet con velocità del fluido lungo il reattore. L’approccio più classico prevede però la scelta della lunghezza L del reattore quale lunghezza di riferimento, cioè zc=L, da cui: � Nell’equazione riconosciamo il tempo di residenza dato che SL è il volume del reattore tubolare e, quindi, ricordando la definizione generale del numero di Damkohler scriviamo: � Osservando l’equazione si può dire che, se la velocità della corrente è relativamente grande, Pe è grande e così il termine di derivata seconda (termine diffusivo) è trascurabile.

PFR isotermo in regime stazionario (7) � Così l’equazione di governo si riduce a: � La (*) esprime l’equazione di bilancio di materia per un reattore PFR ideale in condizioni stazionarie isoterme e nell’ipotesi di volume costante. La reazione avviene con velocità dipendente dalla sola x, grado di conversione (locale). Separando le variabili all’interno della (*) ed integrando ambo i membri si ha: � Comunemente, l’equazione (**) si trova scritta in termini dimensionali, più espressivi in termini delle variabili di progetto e di esercizio: Si può osservare che per qualunque tipo di reattore in flusso le equazioni costitutive mettono in relazione la velocità di reazione, il grado di avanzamento della reazione, il volume del reattore e la portata di alimentazione e, pertanto, ciascuna di queste quattro quantità può essere ricavata conoscendo le altre tre.

PFR isotermo in regime transitorio (1) � Si può scrivere direttamente il bilancio transitorio per l’elementino di spessore dz: dove è stato aggiunto l’accumulo che si ottiene nell’intervallo di tempo finito CSdz. � Come per il modello stazionario, si possono espandere in serie di Taylor termini all’uscita e, dividendo tutto per t e passando al limite per t→ 0, con qualche manipolazione si ottiene: (in rosso il termine di accumulo, aggiunto rispetto al modello stazionario) a cui sono associate le condizioni al contorno e la condizione iniziale:

PFR isotermo in regime transitorio (2) � Per passare alla formulazione adimensionale del modello, prendiamo un tempo caratteristico tc, una lunghezza caratteristica zc ed una concentrazione caratteristica Cc, per esempio C 0. Definiamo quindi le seguenti grandezze adimensionali: da cui: � Sostituendo nell’equazione di bilancio si ha:

PFR isotermo in regime transitorio (3) � Cioè, con qualche manipolazione: � È possibile, con opportuna scelta delle grandezze di riferimento, generare un modello adimensionale universale e privo di parametri a meno del numero di Péclet. Scegliendo quale tempo di riferimento il tempo di residenza (in modo che ) e quale lunghezza di riferimento (in modo che e ricordando la definizione del numero di Peclet � ), si ha: Pertanto, se Pe è grande, il termine di derivata seconda (termine diffusivo) è trascurabile. Ciò accade nella maggior parte dei casi e così l’equazione di governo, corredata delle condizioni al contorno ed iniziale, si riduce a:

PFR isotermo in regime transitorio (4) � Una scelta più comune per la lunghezza di riferimento è, come visto per il modello stazionario, quella di L lunghezza del reattore. Con questa scelta (zc=L), e scegliendo quale tempo di riferimento il tempo di residenza (in modo che ) la (*) diventa: dove, come in precedenza, . Vale anche qui il discorso secondo cui, quando Peclet è grande, l’equazione si semplifica in: a cui si associano le condizioni al contorno ed iniziali:

PFR non isotermo in regime transitorio (1) � Detto DT il coefficiente di diffusione termica, il contributo entrante nel sistema in corrispondenza dell’ascissa z nel tempo t è pari a mentre il contributo uscente in corrispondenza dell’ascissa è pari a . � Raggruppando i termini si ottiene la seguente equazione di bilancio: Energia entrante per convezione entrante per diffusione Energia uscente per diffusione uscente attraverso le pareti Quantità che scompare per reazione uscente per convezione Quantità accumulata

PFR non isotermo in regime transitorio (2) � Il rapporto è la lunghezza (o perimetro) della circonferenza esterna del tubo cilindrico che moltiplicato per dz fornisce l’area della superficie di scambio d. A; infatti si ha: � Come nei casi precedenti, usando l’espansione in serie di Taylor, dividendo tutto per t e dz, e passando al limite per t→ 0 si ottiene: a cui sono associate le condizioni al contorno e la condizione iniziale:

PFR non isotermo in regime transitorio (3) � Per passare alla formulazione adimensionale del modello, prendiamo un tempo caratteristico tc, una lunghezza caratteristica zc ed una concentrazione caratteristica Cc, per esempio C 0. Definiamo quindi le seguenti grandezze adimensionali: � Sostituendo nell’equazione di bilancio si ha:

PFR non isotermo in regime transitorio (4) � cioè: � È possibile, con opportuna scelta delle grandezze di riferimento, generare un modello adimensionale universale e privo di parametri a meno del numero di Péclet. 1) si scelga quale tempo di riferimento il tempo di residenza (in modo che ) 2) si scelga quale lunghezza di riferimento (in modo che ) 3) si introduca la definizione del numero di Peclet termico

PFR non isotermo in regime transitorio (4) � si ha: dove: � Pertanto, se Pe. T è grande, il termine di derivata seconda (termine diffusivo) è trascurabile. Ciò accade nella maggior parte dei casi e così l’equazione di governo, corredata delle condizioni al contorno ed iniziale, si riduce a:

PFR non isotermo in regime transitorio (6) � Una scelta più comune per la lunghezza di riferimento è, come visto per il modello stazionario, quella di L lunghezza del reattore. Con questa scelta (zc=L), e scegliendo quale tempo di riferimento il tempo di residenza (in modo che ) la (*) diventa: dove, come in precedenza, . Vale anche qui il discorso secondo cui, quando Peclet è grande, l’equazione si semplifica in: a cui si associano le condizioni al contorno ed iniziali:

PRF non isotermo in regime transitorio (7) � Riportiamo l’equazione di bilancio di materia e quindi le due equazioni si scrivono come: con relative condizioni al contorno ed iniziali:

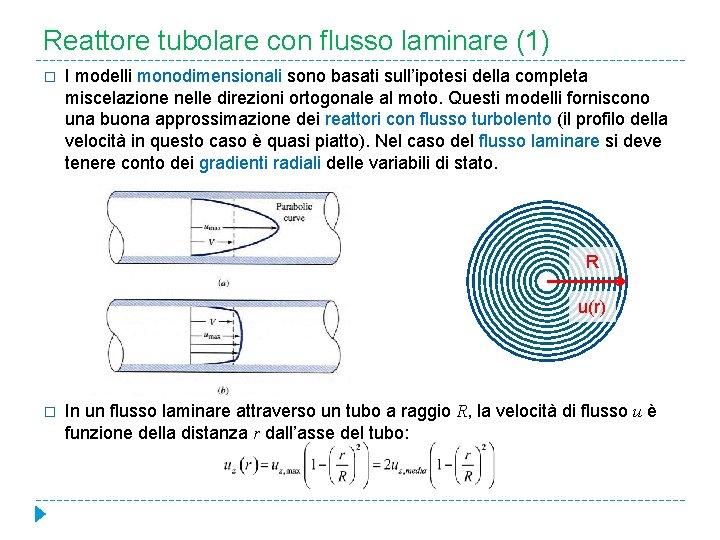
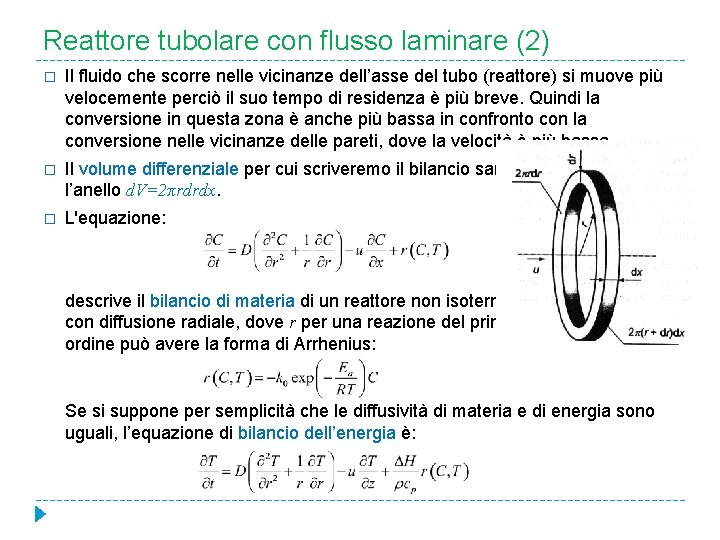
Reattore tubolare con flusso laminare (1) � I modelli monodimensionali sono basati sull’ipotesi della completa miscelazione nelle direzioni ortogonale al moto. Questi modelli forniscono una buona approssimazione dei reattori con flusso turbolento (il profilo della velocità in questo caso è quasi piatto). Nel caso del flusso laminare si deve tenere conto dei gradienti radiali delle variabili di stato. R u(r) � In un flusso laminare attraverso un tubo a raggio R, la velocità di flusso u è funzione della distanza r dall’asse del tubo:

Reattore tubolare con flusso laminare (2) � Il fluido che scorre nelle vicinanze dell’asse del tubo (reattore) si muove più velocemente perciò il suo tempo di residenza è più breve. Quindi la conversione in questa zona è anche più bassa in confronto con la conversione nelle vicinanze delle pareti, dove la velocità è più bassa. � Il volume differenziale per cui scriveremo il bilancio sarà l’anello d. V=2πrdrdx. � L'equazione: descrive il bilancio di materia di un reattore non isotermo con diffusione radiale, dove r per una reazione del primo ordine può avere la forma di Arrhenius: Se si suppone per semplicità che le diffusività di materia e di energia sono uguali, l’equazione di bilancio dell’energia è: