Modeliranje dinamike sustava Prostor stanja Studeni 2013 Modeliranje

Modeliranje dinamike sustava Prostor stanja Studeni 2013

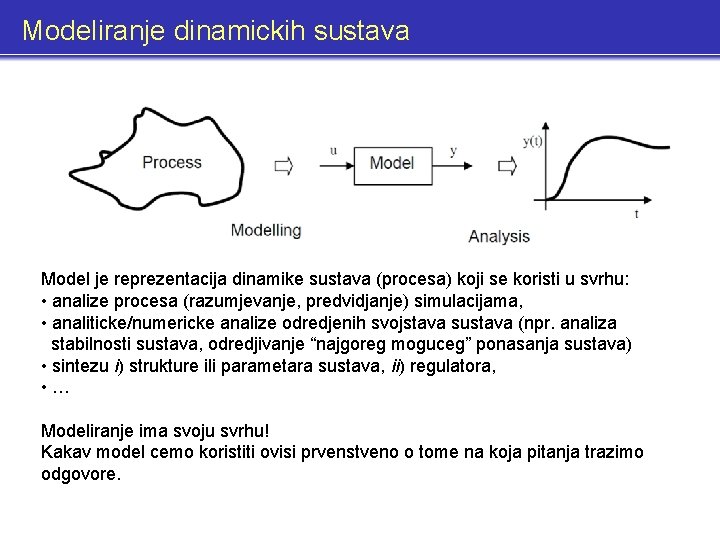
Modeliranje dinamickih sustava Model je reprezentacija dinamike sustava (procesa) koji se koristi u svrhu: • analize procesa (razumjevanje, predvidjanje) simulacijama, • analiticke/numericke analize odredjenih svojstava sustava (npr. analiza stabilnosti sustava, odredjivanje “najgoreg moguceg” ponasanja sustava) • sintezu i) strukture ili parametara sustava, ii) regulatora, • … Modeliranje ima svoju svrhu! Kakav model cemo koristiti ovisi prvenstveno o tome na koja pitanja trazimo odgovore.

Modeliranje dinamickih sustava Matematicki modeli – opis sustava jednadzbama 1) Algebarske jednadzbe -“trenutan” odnos medju varijablama (f=k q sila u opruzi) 2) Differencijalne jednadzbe -Važno je vremensko ponašanje varijabli - Stvari se ne dešavaju trenutno (imaju memoriju, spremike (energije), “za promjenu treba vremena”) Primjeri: - glavobolja ne nestaje odmah cim uzmemo aspirin - kondenzator se moze isprazniti spajanjem otpornika – ali ne trenutno - stiskanjem pedale gasa postize se veca brzina – ali ne trenutno - temperatura u sobi ne naraste isti tren kad smo ukljucili grijanje - investicije ne nose trenutnu zaradu, vec ovaj proces ima svoju dinamiku Za dinamicke sustave ima smisla pitati “u kojem su trenutno stanju”? U sirem smislu, i ucenje je dinamicki proces…

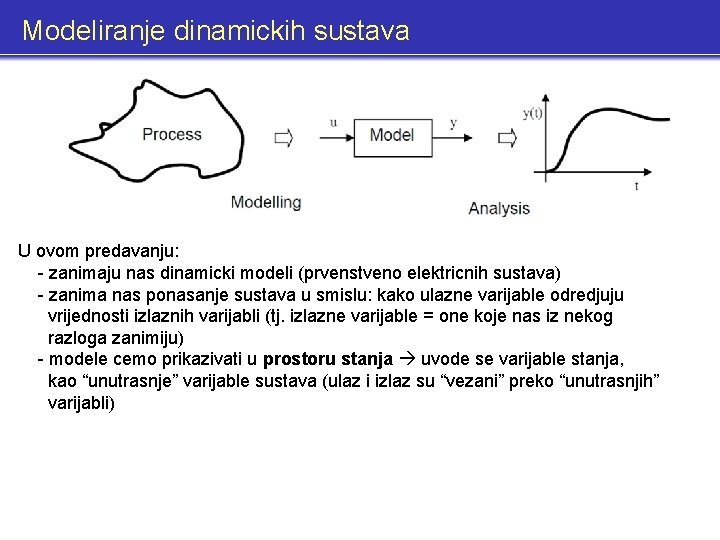
Modeliranje dinamickih sustava U ovom predavanju: - zanimaju nas dinamicki modeli (prvenstveno elektricnih sustava) - zanima nas ponasanje sustava u smislu: kako ulazne varijable odredjuju vrijednosti izlaznih varijabli (tj. izlazne varijable = one koje nas iz nekog razloga zanimiju) - modele cemo prikazivati u prostoru stanja uvode se varijable stanja, kao “unutrasnje” varijable sustava (ulaz i izlaz su “vezani” preko “unutrasnjih” varijabli)

Modeliranje dinamickih sustava “Nasljeđe mehaničara” (povijesno): Kepler, Newton: gibanje planeta, gravitacija, Newtonovi aksiomi Jedan od trijmufa Newtonove mahanike: gibanje planeta moze se predvidjeti uz poznavanje trenutnih polozaja i brzina (to je dovoljno informacija za proracunati buducnost, a sve sto trebamo znati o proslosti “sadrzano je” u polozajima i brzinama. ) Napomena: ovdje se radi o autonomnom sustavu; nema vanjskih pobuda (ulaza)

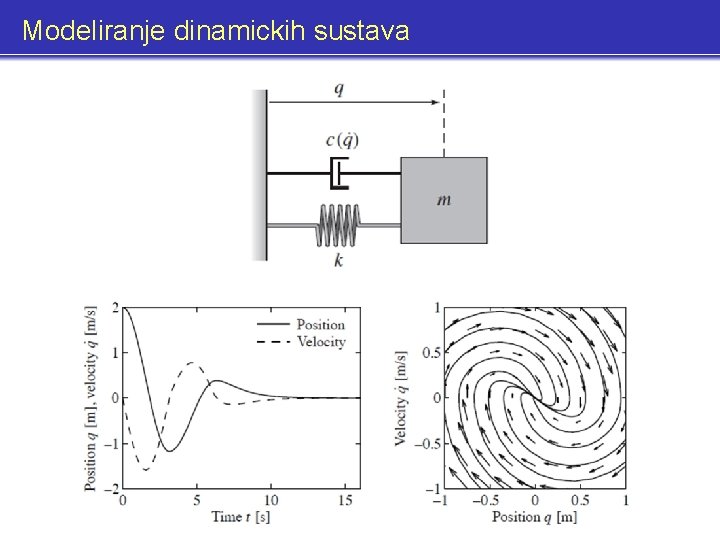
Modeliranje dinamickih sustava fazni portret (phase portrait) Stanje sustava (vektor stanja sustava; varijable stanje sustava): = skup svih varijabli koje potpuno definiraju gibanje sustava (koje su dovoljne za prdvidjanje buducnosti sustava) Za sustava sa gornje slike: Skup svih mogucih vrijednosti vektora stanja: prostor stanja

Modeliranje dinamickih sustava

Modeliranje dinamickih sustava fazni portret (phase portrait) Autonoman sustav: Neautonoman sustav (ima vanjske ulaze; vanjske pobude, poremecaje):

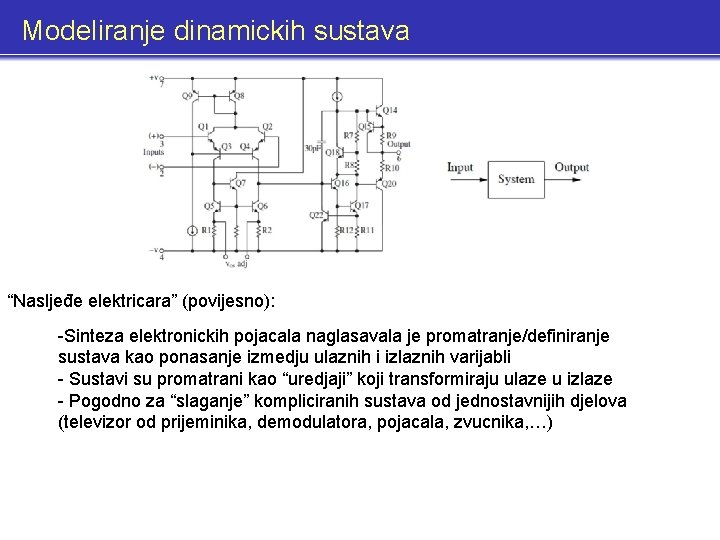
Modeliranje dinamickih sustava “Nasljeđe elektricara” (povijesno): -Sinteza elektronickih pojacala naglasavala je promatranje/definiranje sustava kao ponasanje izmedju ulaznih i izlaznih varijabli - Sustavi su promatrani kao “uredjaji” koji transformiraju ulaze u izlaze - Pogodno za “slaganje” kompliciranih sustava od jednostavnijih djelova (televizor od prijeminika, demodulatora, pojacala, zvucnika, …)

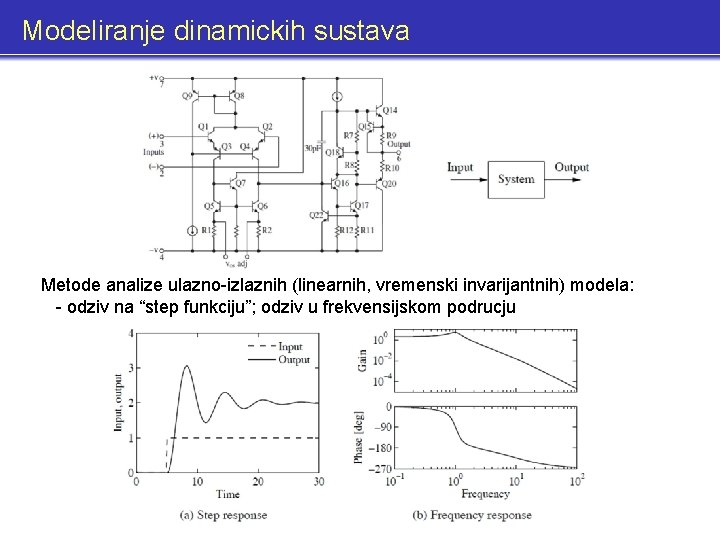
Modeliranje dinamickih sustava Metode analize ulazno-izlaznih (linearnih, vremenski invarijantnih) modela: - odziv na “step funkciju”; odziv u frekvensijskom podrucju

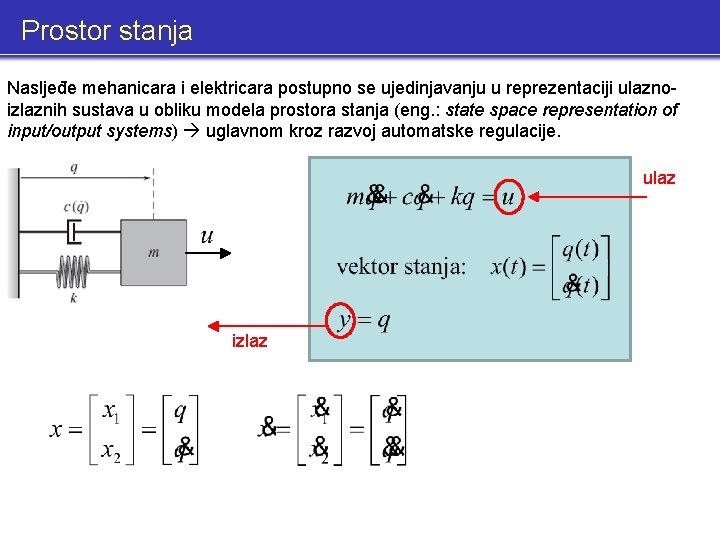
Prostor stanja Nasljeđe mehanicara i elektricara postupno se ujedinjavanju u reprezentaciji ulaznoizlaznih sustava u obliku modela prostora stanja (eng. : state space representation of input/output systems) uglavnom kroz razvoj automatske regulacije. ulaz izlaz

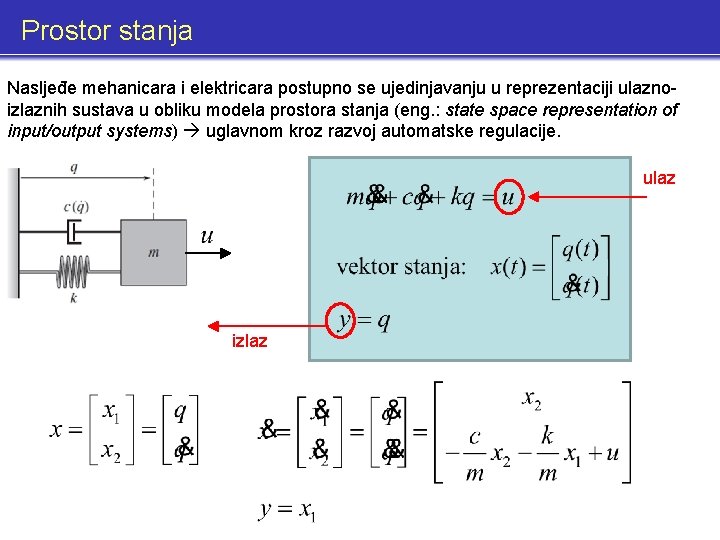
Prostor stanja Nasljeđe mehanicara i elektricara postupno se ujedinjavanju u reprezentaciji ulaznoizlaznih sustava u obliku modela prostora stanja (eng. : state space representation of input/output systems) uglavnom kroz razvoj automatske regulacije. ulaz izlaz

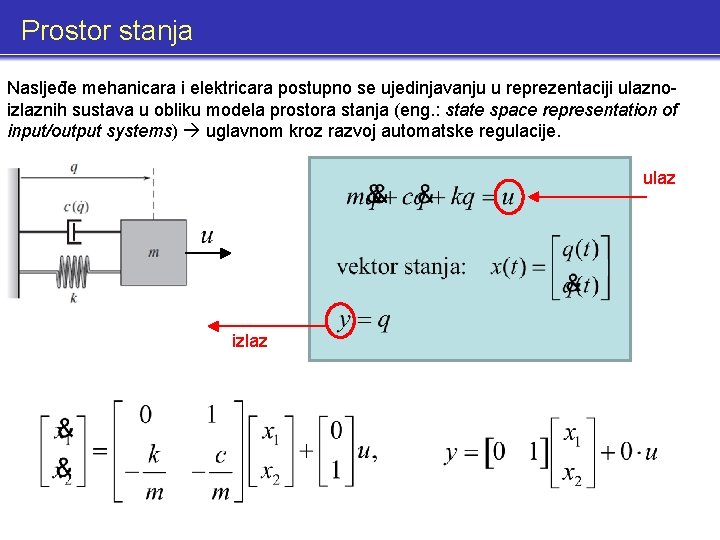
Prostor stanja Nasljeđe mehanicara i elektricara postupno se ujedinjavanju u reprezentaciji ulaznoizlaznih sustava u obliku modela prostora stanja (eng. : state space representation of input/output systems) uglavnom kroz razvoj automatske regulacije. ulaz izlaz

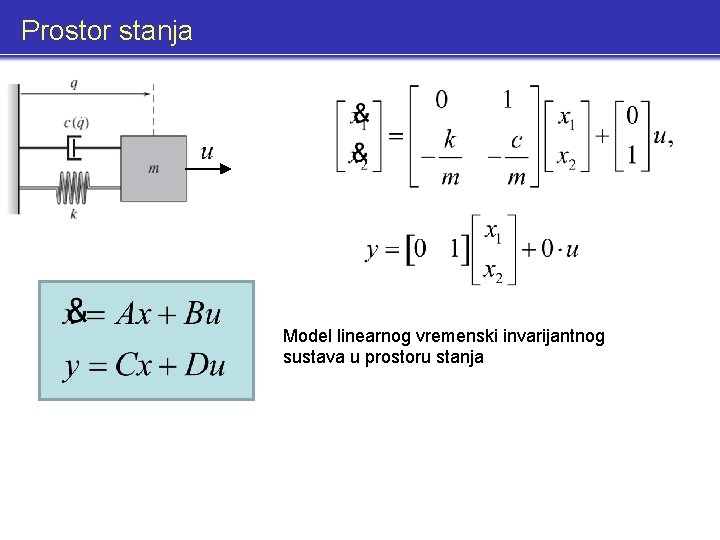
Prostor stanja Model linearnog vremenski invarijantnog sustava u prostoru stanja

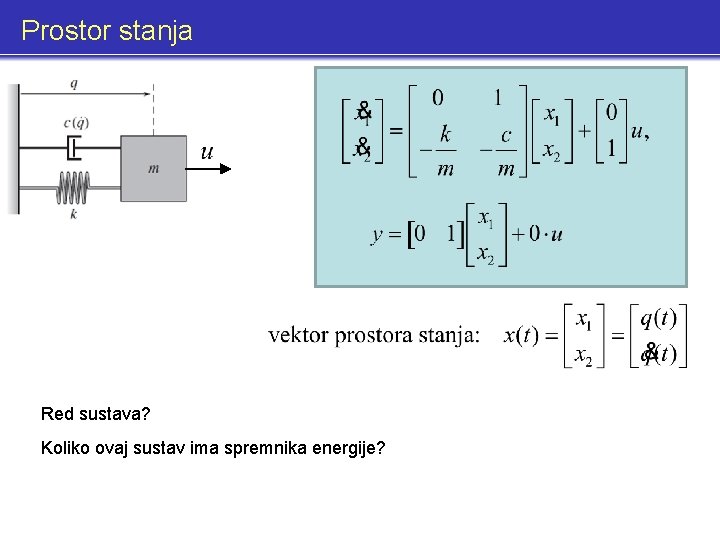
Prostor stanja Model linearnog vremenski invarijantnog sustava u prostoru stanja Model linearnog vremenski promjenjvog sustava u prostoru stanja Model nelinearnog sustava u prostoru stanja = vektor prostora stanja = red sustava

Prostor stanja Red sustava? Koliko ovaj sustav ima spremnika energije?

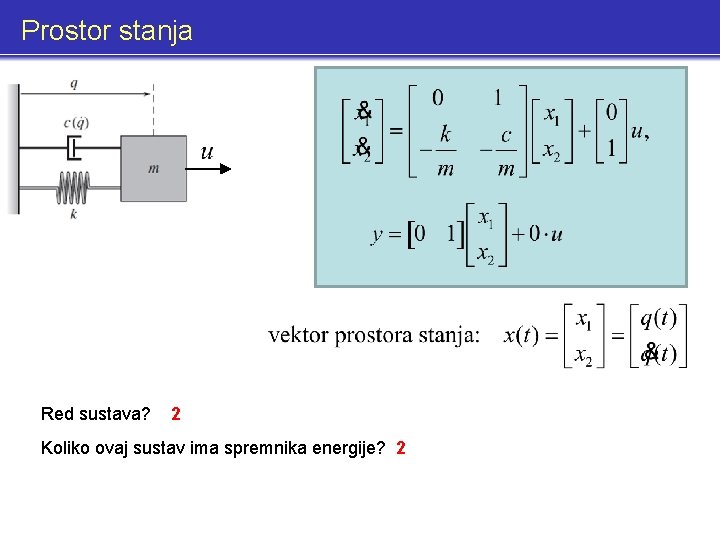
Prostor stanja Red sustava? 2 Koliko ovaj sustav ima spremnika energije? 2

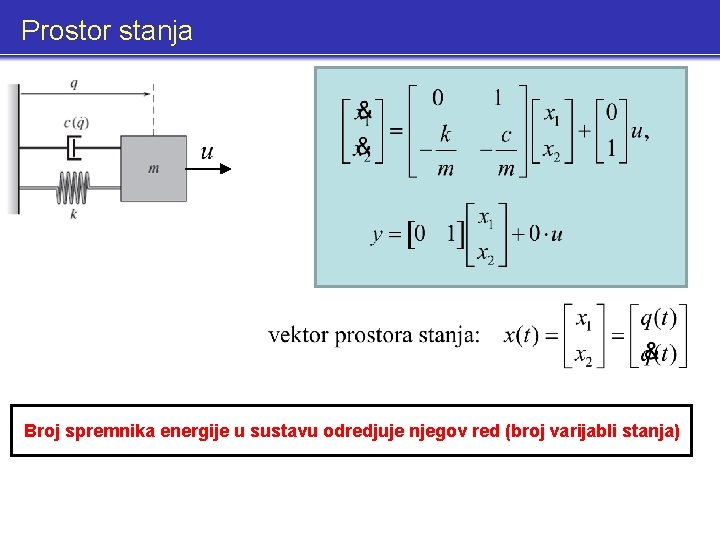
Prostor stanja

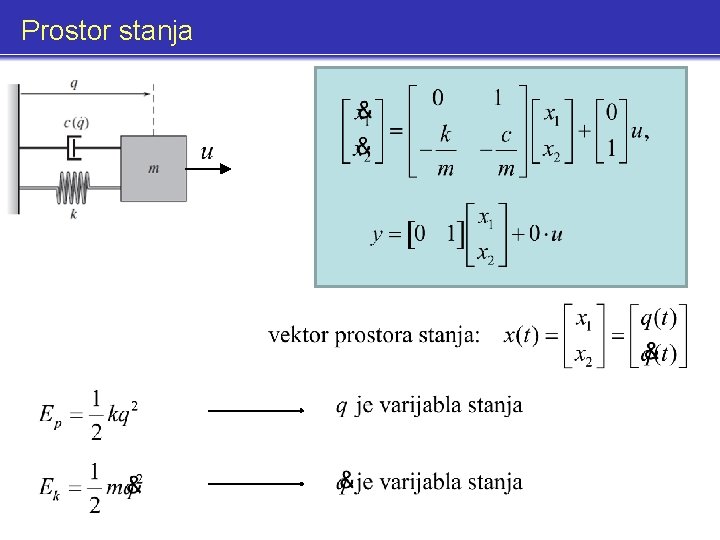
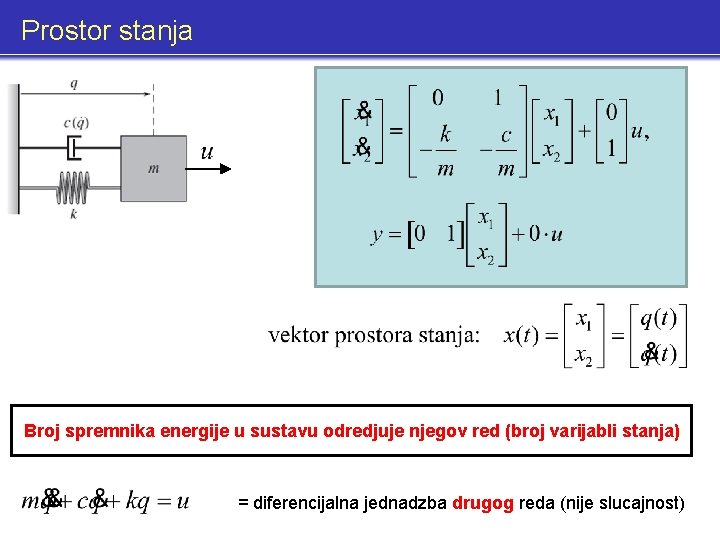
Prostor stanja Broj spremnika energije u sustavu odredjuje njegov red (broj varijabli stanja)

Prostor stanja Broj spremnika energije u sustavu odredjuje njegov red (broj varijabli stanja) = diferencijalna jednadzba drugog reda (nije slucajnost)

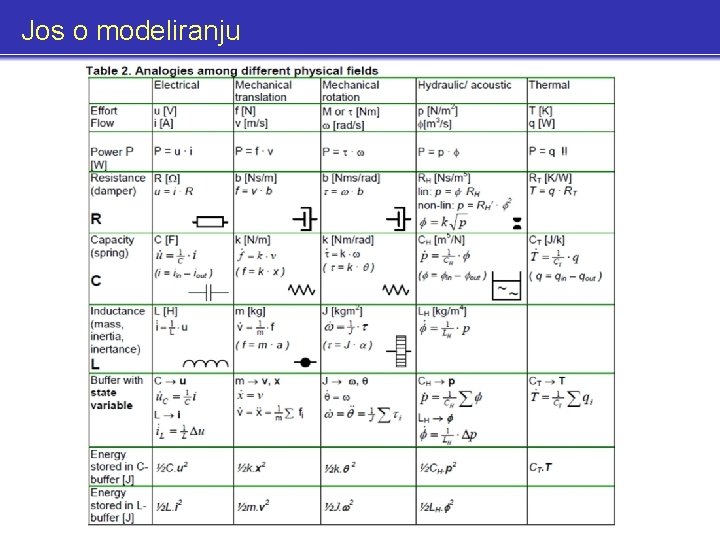
Jos o modeliranju

Jos o modeliranju

Jos o modeliranju

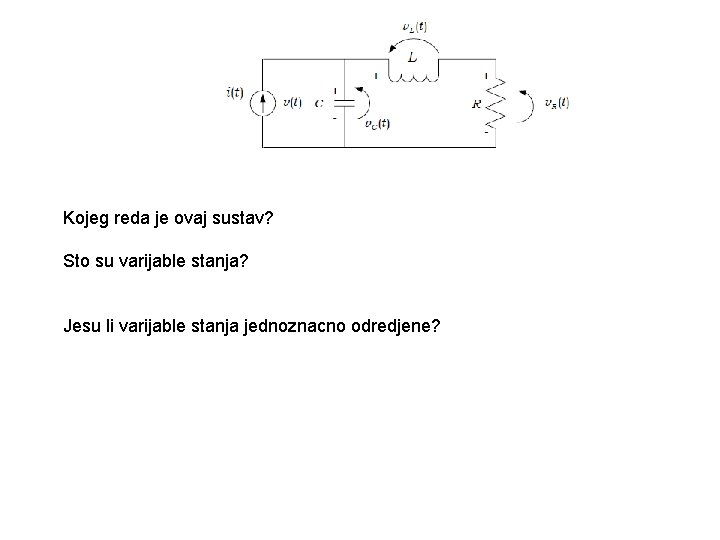
Kojeg reda je ovaj sustav? Sto su varijable stanja? Jesu li varijable stanja jednoznacno odredjene?

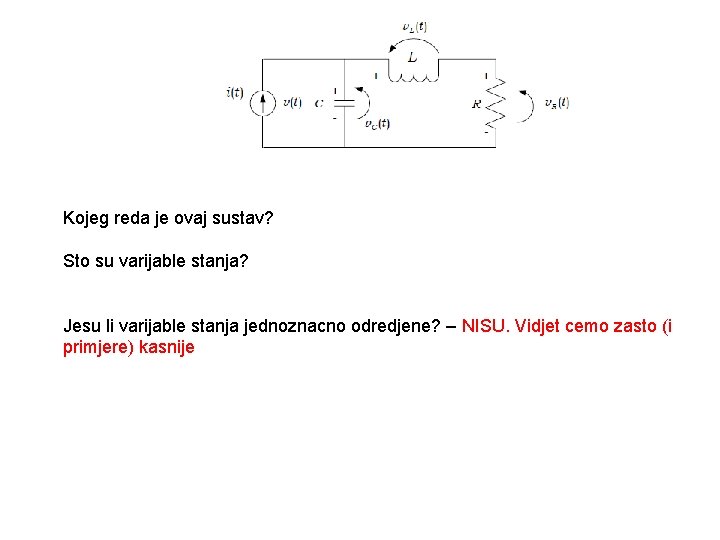
Kojeg reda je ovaj sustav? Sto su varijable stanja? Jesu li varijable stanja jednoznacno odredjene? – NISU. Vidjet cemo zasto (i primjere) kasnije

Jos o modeliranju

Modeliranje dinamickih sustava (mehatronika) • R resistance • L inductance • J moment of inertia • B mechanical damping

Modeliranje dinamickih sustava (mehatronika) • R resistance • L inductance • J moment of inertia • B mechanical damping

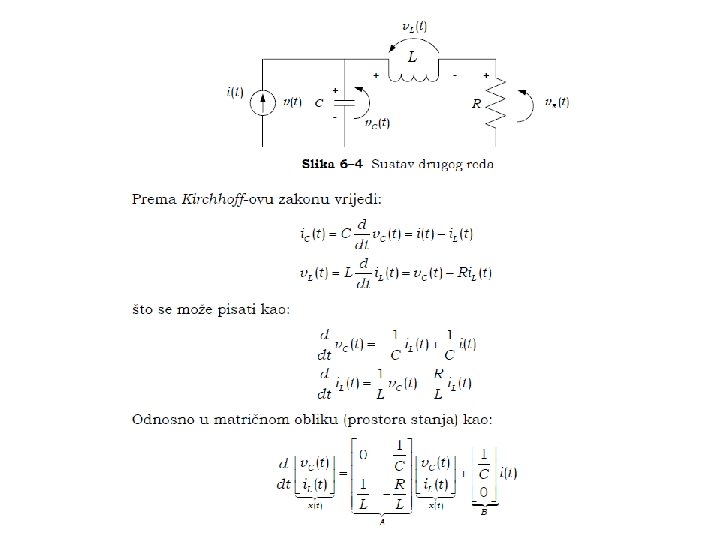
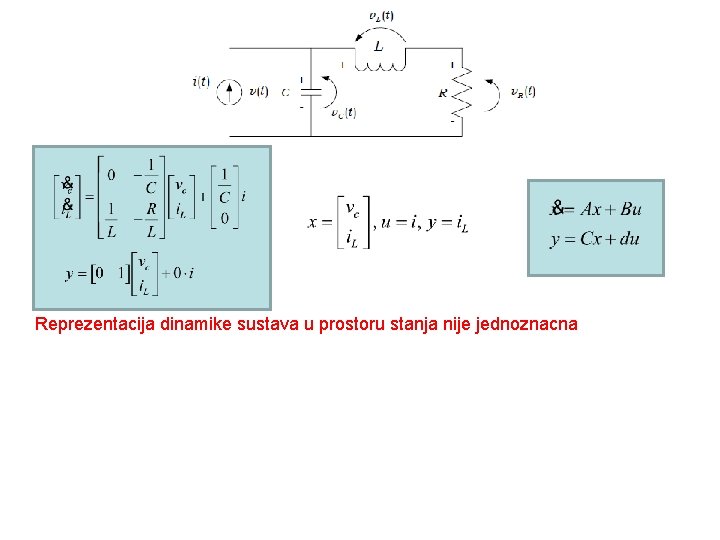
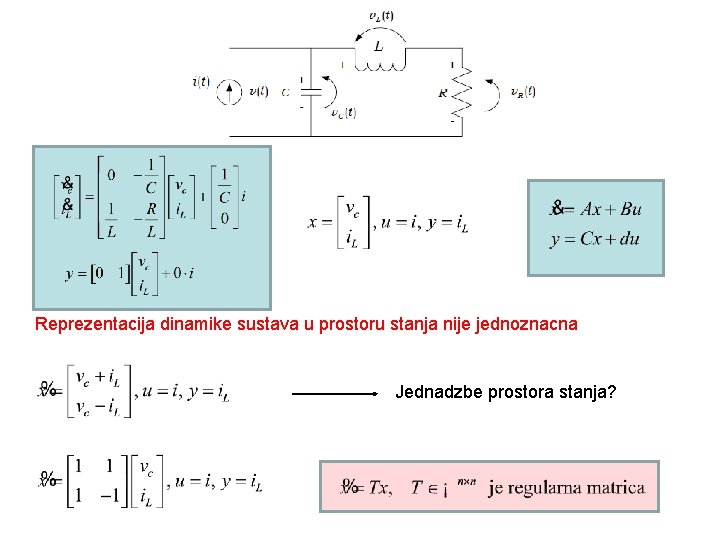
Reprezentacija dinamike sustava u prostoru stanja nije jednoznacna

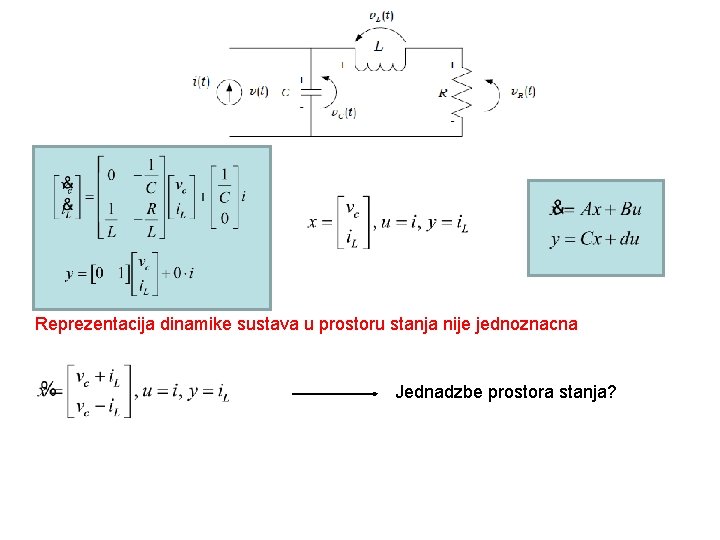
Reprezentacija dinamike sustava u prostoru stanja nije jednoznacna Jednadzbe prostora stanja?

Reprezentacija dinamike sustava u prostoru stanja nije jednoznacna Jednadzbe prostora stanja?

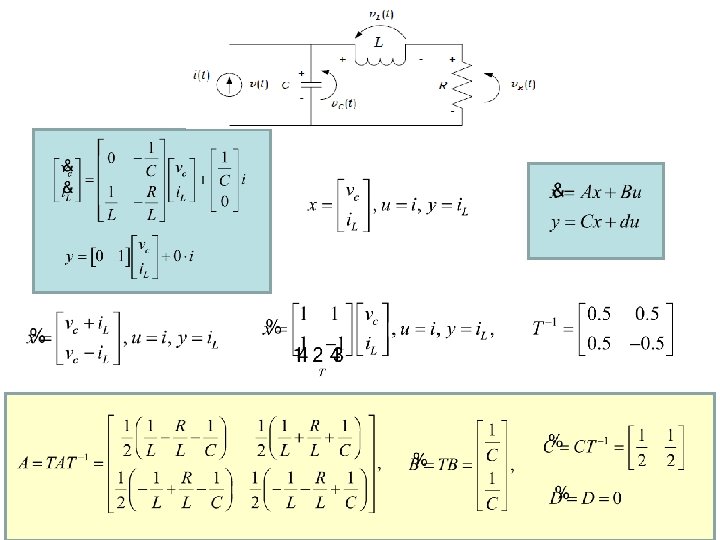
Reprezentacija dinamike sustava u prostoru stanja nije jednoznacna

Reprezentacija dinamike sustava u prostoru stanja nije jednoznacna

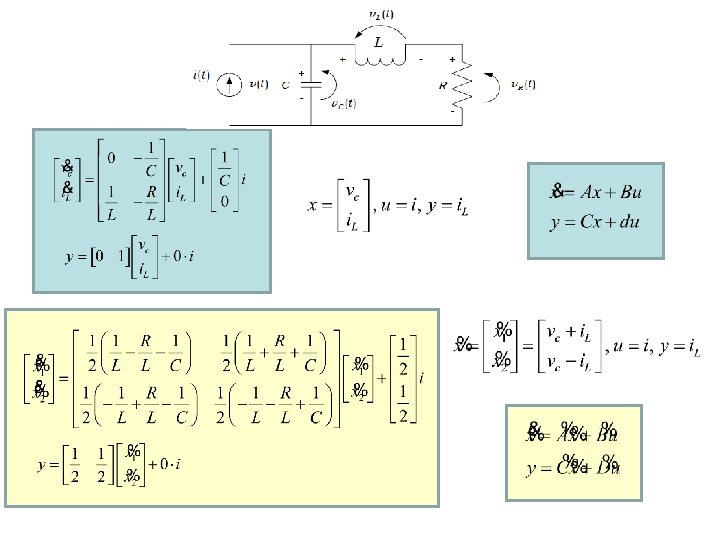
Reprezentacija dinamike sustava u prostoru stanja nije jednoznacna

Reprezentacija dinamike sustava u prostoru stanja nije jednoznacna

Reprezentacija dinamike sustava u prostoru stanja nije jednoznacna

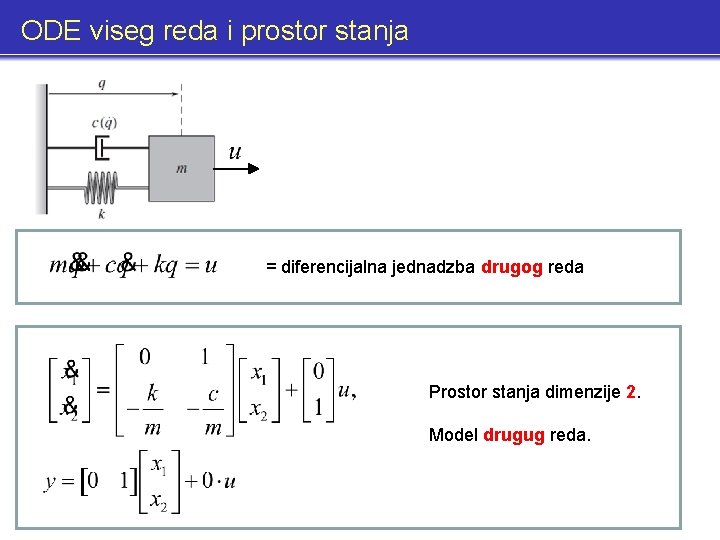
ODE viseg reda i prostor stanja = diferencijalna jednadzba drugog reda Prostor stanja dimenzije 2. Model drugug reda.

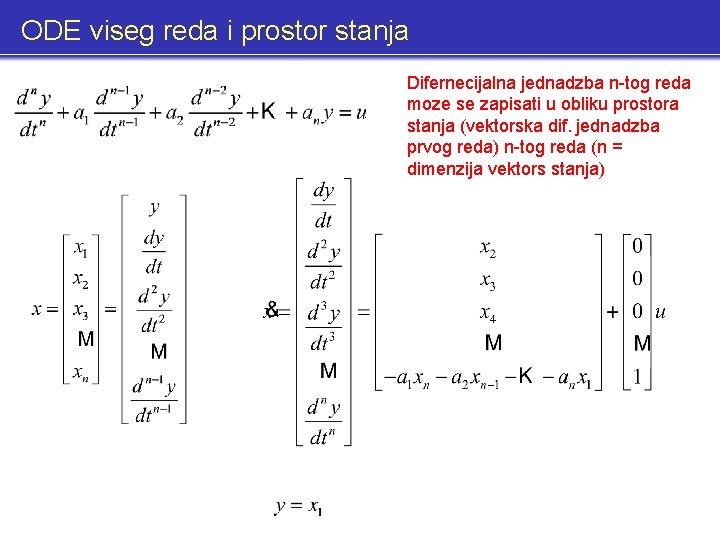
ODE viseg reda i prostor stanja Difernecijalna jednadzba n-tog reda moze se zapisati u obliku prostora stanja (vektorska dif. jednadzba prvog reda) n-tog reda (n = dimenzija vektors stanja)

ODE viseg reda i prostor stanja Difernecijalna jednadzba n-tog reda moze se zapisati u obliku prostora stanja (vektorska dif. jednadzba prvog reda) n-tog reda (n = dimenzija vektors stanja)

Primjer

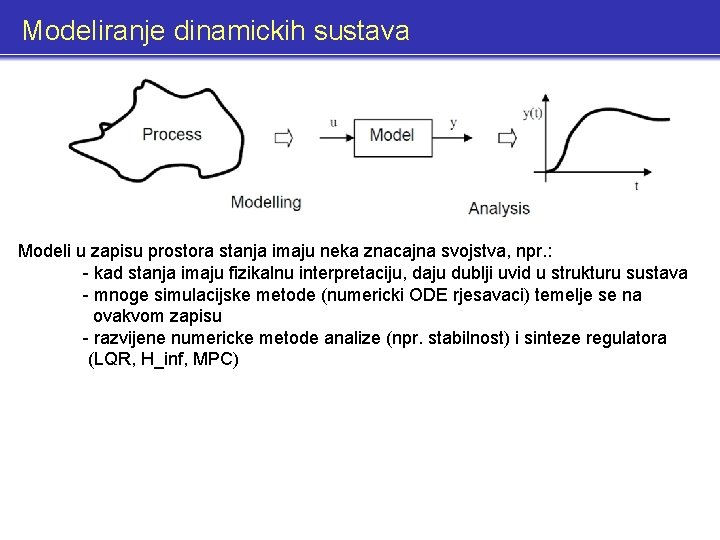
Modeliranje dinamickih sustava Modeli u zapisu prostora stanja imaju neka znacajna svojstva, npr. : - kad stanja imaju fizikalnu interpretaciju, daju dublji uvid u strukturu sustava - mnoge simulacijske metode (numericki ODE rjesavaci) temelje se na ovakvom zapisu - razvijene numericke metode analize (npr. stabilnost) i sinteze regulatora (LQR, H_inf, MPC)