Modeling with Differential Equations Dr Jeff Morgan Department

Modeling with Differential Equations Dr. Jeff Morgan Department of Mathematics University of Houston jmorgan@math. uh. edu

Shameless Advertisement • Houston Area Calculus Teachers Association – http: //www. Houston. ACT. org • Houston Area Teachers of Statistics – http: //www. Houston. ATS. org • Online practice AP Calculus and Statistics Exams – April and May 2009. See the links above. • UH High School Mathematics Contest – http: //mathcontest. uh. edu • teach. HOUSTON – http: //teach. HOUSTON. uh. edu • Online Masters in Mathematics http: //www. math. uh. edu/Matweb/grad_mam. htm

Goals • Create a mathematical model for the motion of a cart along an arbitrary roller coaster track lying in the xy plane, subject to gravity in the -y direction. • Examine the specific case of a circular track, and build an animation of the motion. • Consider the added complexity of a spring loaded roller coaster model, and modify the mathematical model. • Determine whethere is a spring loaded model on which the speed of the cart would always be constant. • Modify the spring model to incorporate a bungee cord.

A Review of Projection and Component u u v v

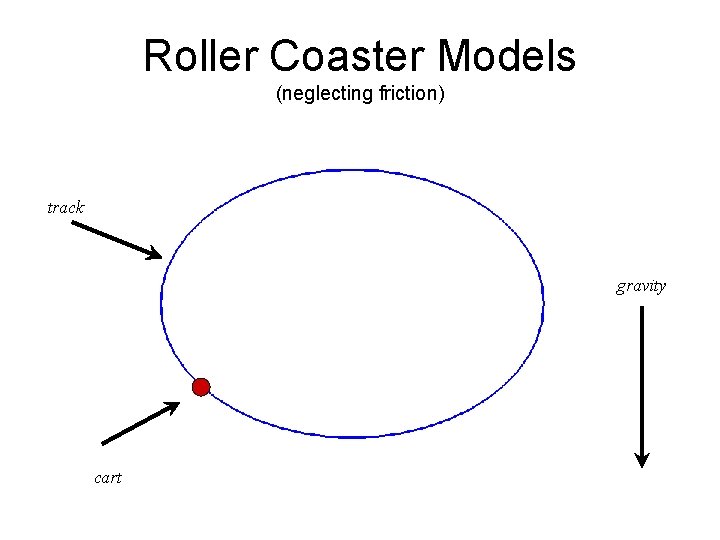
Roller Coaster Models (neglecting friction) track gravity cart

Creating the Mathematical Model

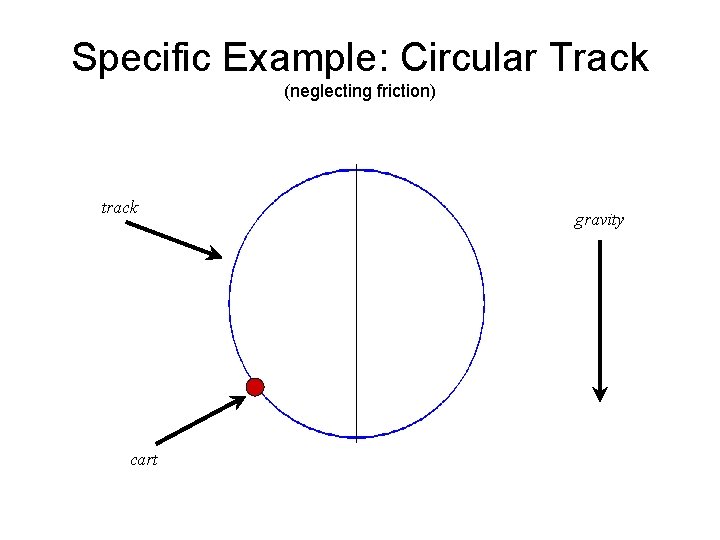
Specific Example: Circular Track (neglecting friction) track cart gravity

Process • • • Write Model Equations. Solve using Winplot. Export data to Excel. Fit Data. Animate the motion in Winplot.

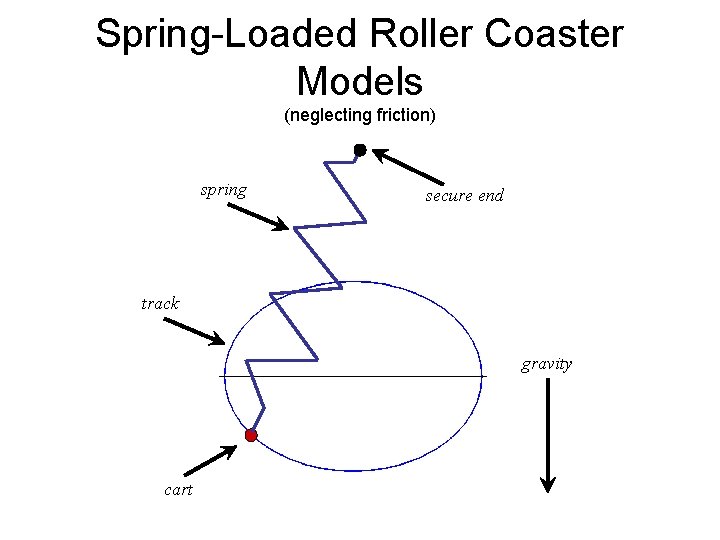
Spring-Loaded Roller Coaster Models (neglecting friction) spring secure end track gravity cart

Creating the Mathematical Model

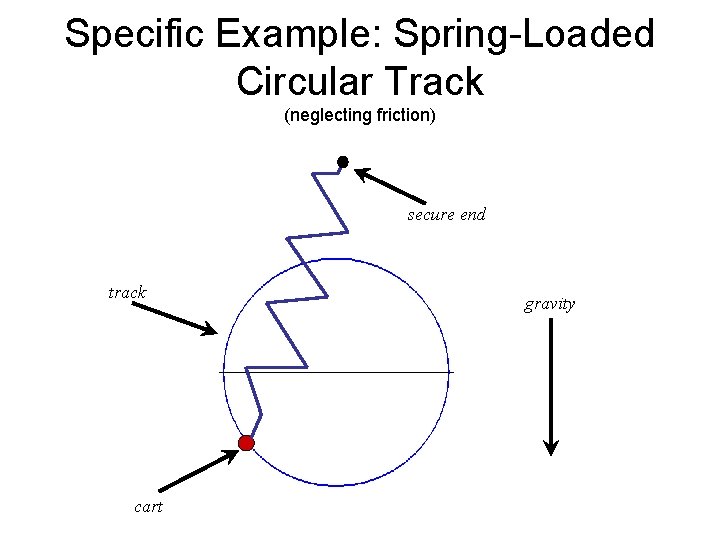
Specific Example: Spring-Loaded Circular Track (neglecting friction) secure end track cart gravity

Process • Write Model Equations. • Explore using Winplot. • Discuss animating the motion.

Exploration: Determine whethere a spring-loaded roller track so that the speed of the cart along the track is always constant.

Exploration: How will the model change if we use a bungee cord instead of a spring?

An Important Example: Displacement (meters) Force (Newtons) . 01. 02 . 21. 42 . 03. 05. 06. 08. 10. 13. 16. 18. 21. 25 . 63. 83 1. 0 1. 3 1. 5 1. 7 1. 9 2. 1 2. 3 2. 5

Exploration: Determine whethere a bungee coaster roller track so that the speed of the cart along the track is always constant.