Modeling Transformation Overview n 2 D Transformation Basic

Modeling Transformation

Overview n 2 D Transformation Ø Basic 2 D transformations Ø Matrix representation Ø Matrix Composition n 3 D Transformation Ø Basic 3 D transformations Ø Same as 2 D n Transformation Hierarchies Ø Scene graphs Ø Ray casting
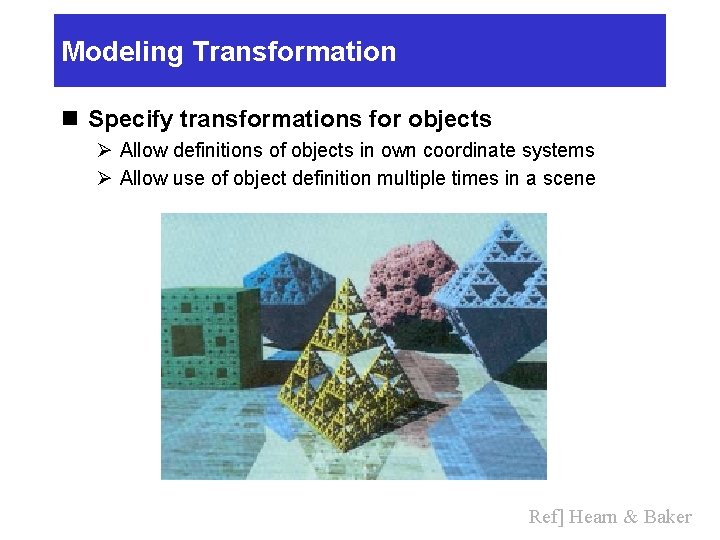
Modeling Transformation n Specify transformations for objects Ø Allow definitions of objects in own coordinate systems Ø Allow use of object definition multiple times in a scene Ref] Hearn & Baker
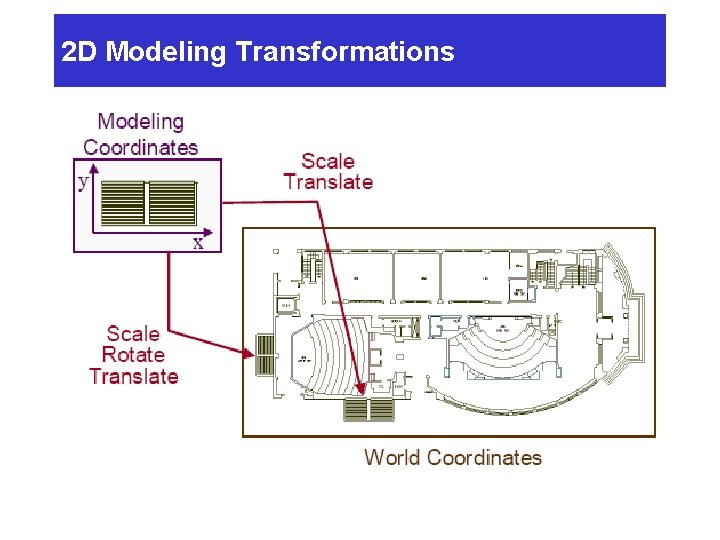
2 D Modeling Transformations
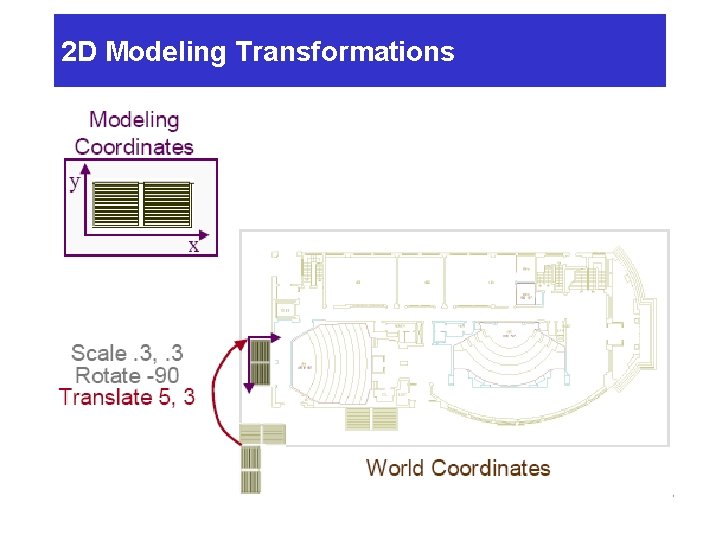
2 D Modeling Transformations
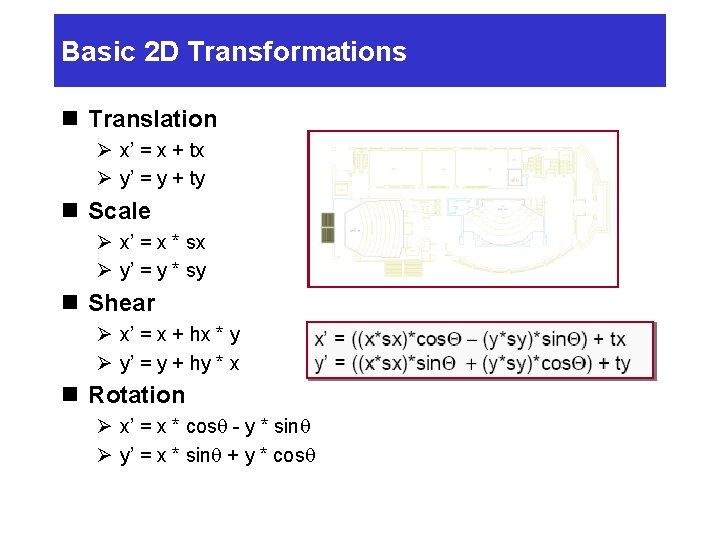
Basic 2 D Transformations n Translation Ø x’ = x + tx Ø y’ = y + ty n Scale Ø x’ = x * sx Ø y’ = y * sy n Shear Ø x’ = x + hx * y Ø y’ = y + hy * x n Rotation Ø x’ = x * cosq - y * sinq Ø y’ = x * sinq + y * cosq

Matrix Representation n Represent 2 D transformation by a matrix n Multiply matrix by column vector Ø Apply transformation to point

Matrix Representation n Transformations combined by multiplication Ø Matrices are a convenient and efficient way to represent a sequence of transformations

2 x 2 Matrices n What types of transformations can be represented with a 2 x 2 matrix? Ø 2 D Identity Ø 2 D Scale around (0, 0)

2 x 2 Matrices n What types of transformations can be represented with a 2 x 2 matrix? Ø 2 D Rotate around (0, 0) Ø 2 D Shear shx = 2

2 x 2 Matrices n What types of transformations can be represented with a 2 x 2 matrix? Ø 2 D Mirror (=Reflection) over Y axis Ø 2 D Mirror over (0, 0)

2 x 2 Matrices n What types of transformations can be represented with a 2 x 2 matrix? Ø 2 D Translation ? NO! Only linear 2 D transformation can be presented with a 2 x 2 matrix

Linear Transformations n Linear transformations are combinations of … Ø Ø Scale Rotation Shear Mirror (=Reflection) n Properties of linear transformations Ø Ø Ø Satisfies: Origin maps to origin Lines map to lines Parallel line remain parallel Ratios are preserved Closed under composition

2 D Translation n 2 D Translation represented by a 3 x 3 matrix Ø Point represented with homogeneous coordinate

Homogeneous Coordinates n Add a 3 rd coordinate to every 2 D point Ø (x, y, w) represents a point at location (x/w, y/w) Ø (x, y, 0) represents a point at infinity Ø (0, 0, 0) is not allowed
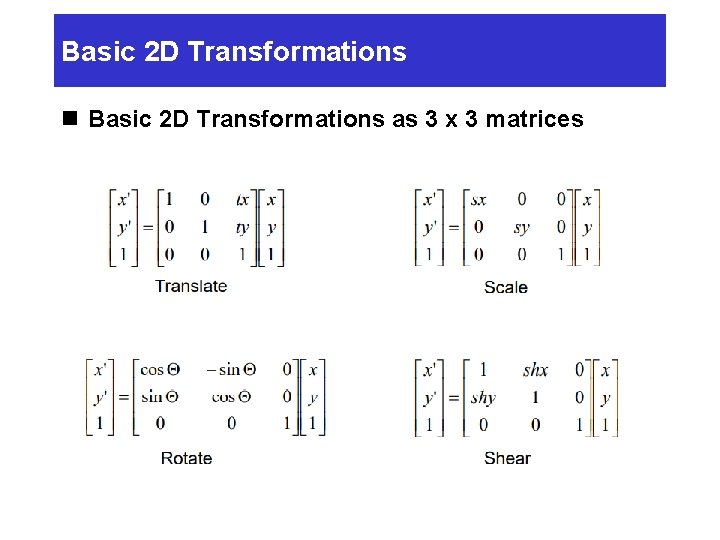
Basic 2 D Transformations n Basic 2 D Transformations as 3 x 3 matrices
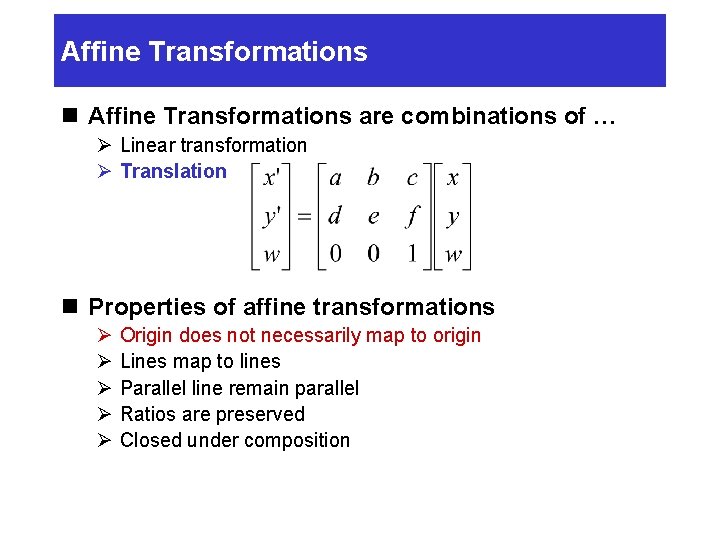
Affine Transformations n Affine Transformations are combinations of … Ø Linear transformation Ø Translation n Properties of affine transformations Ø Ø Ø Origin does not necessarily map to origin Lines map to lines Parallel line remain parallel Ratios are preserved Closed under composition
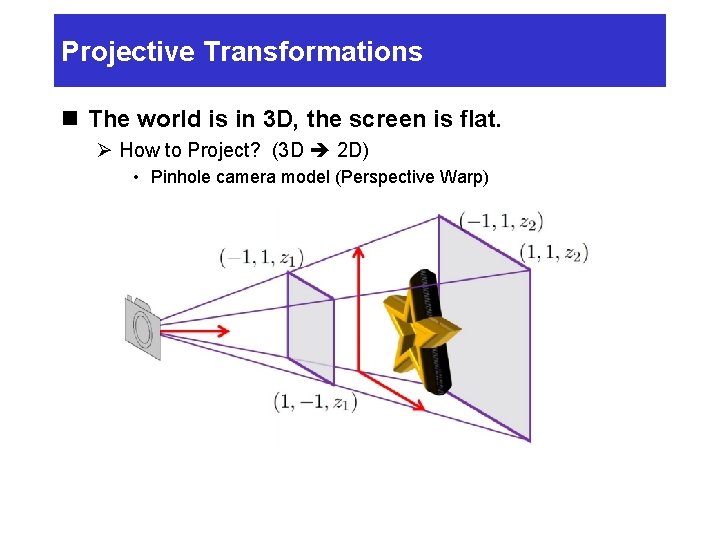
Projective Transformations n The world is in 3 D, the screen is flat. Ø How to Project? (3 D 2 D) • Pinhole camera model (Perspective Warp)

Projective Transformations n Perspective warp in art

Projective Transformations n Projective Transformations … Ø Affine transformation Ø Projective warps n Properties of projective transformations Ø Ø Ø Origin does not necessarily map to origin Lines map to lines Parallel line do not necessarily remain parallel Ratios are not preserved Closed under composition
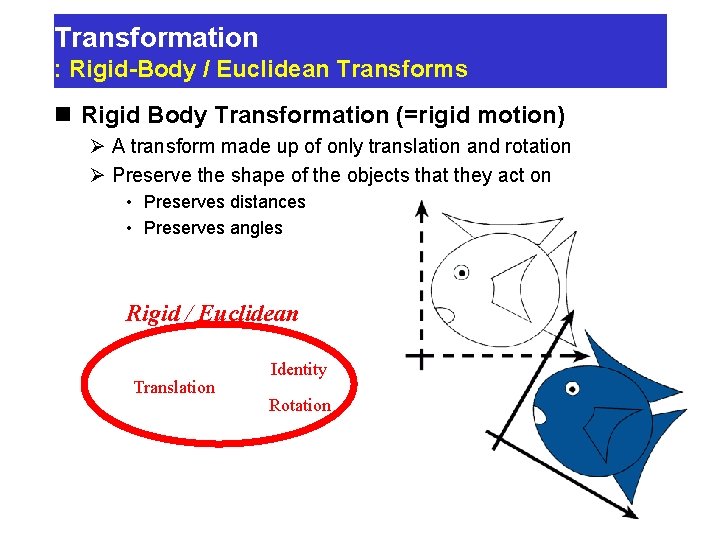
Transformation : Rigid-Body / Euclidean Transforms n Rigid Body Transformation (=rigid motion) Ø A transform made up of only translation and rotation Ø Preserve the shape of the objects that they act on • Preserves distances • Preserves angles Rigid / Euclidean Translation Identity Rotation
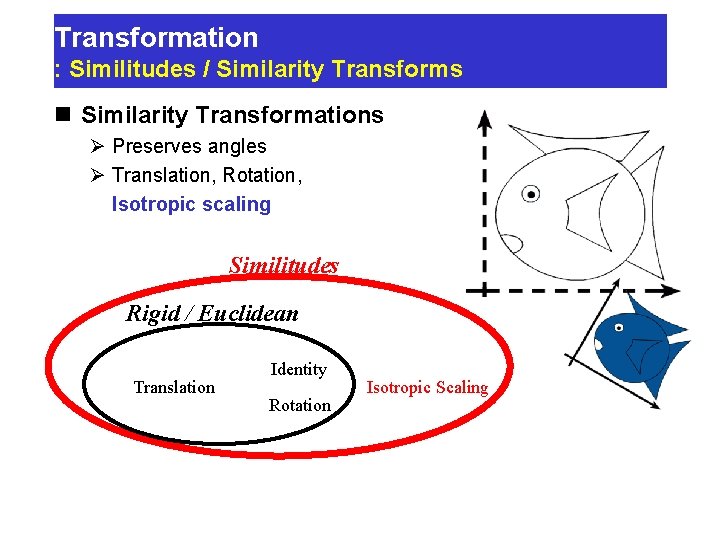
Transformation : Similitudes / Similarity Transforms n Similarity Transformations Ø Preserves angles Ø Translation, Rotation, Isotropic scaling Similitudes Rigid / Euclidean Translation Identity Rotation Isotropic Scaling
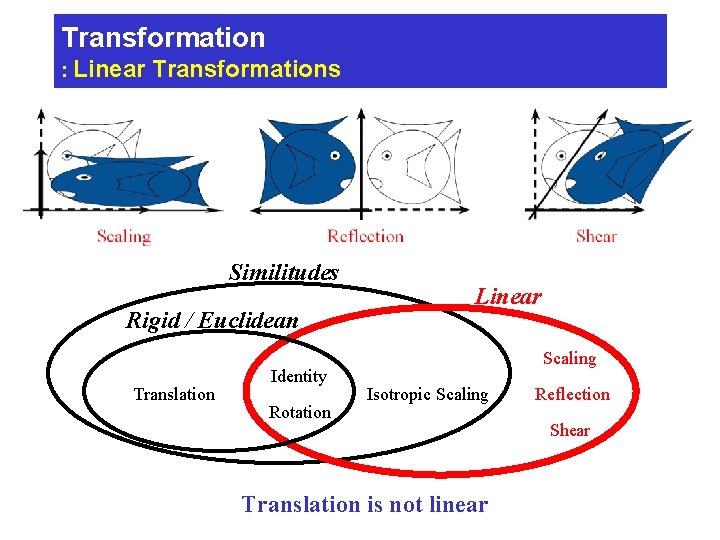
Transformation : Linear Transformations Similitudes Rigid / Euclidean Translation Identity Rotation Linear Scaling Isotropic Scaling Translation is not linear Reflection Shear
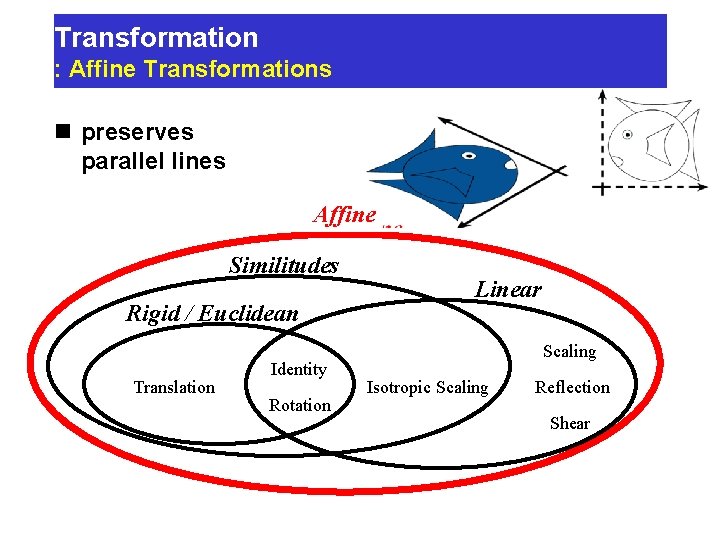
Transformation : Affine Transformations n preserves parallel lines Affine Similitudes Rigid / Euclidean Translation Identity Rotation Linear Scaling Isotropic Scaling Reflection Shear
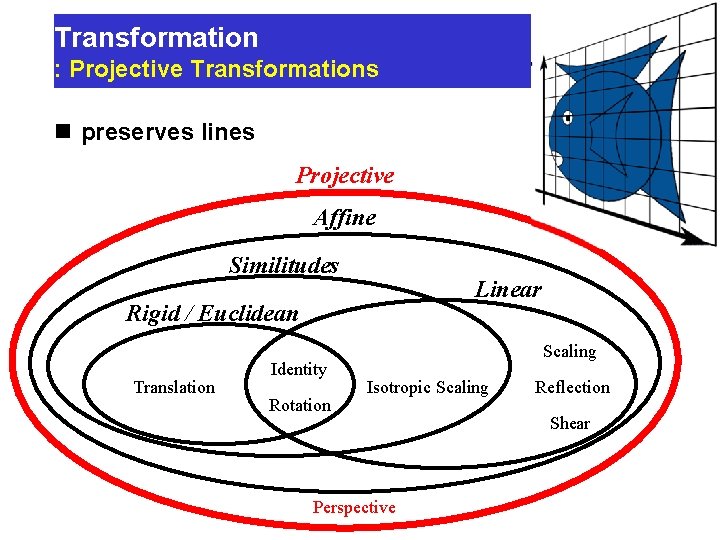
Transformation : Projective Transformations n preserves lines Projective Affine Similitudes Linear Rigid / Euclidean Translation Identity Rotation Scaling Isotropic Scaling Perspective Reflection Shear
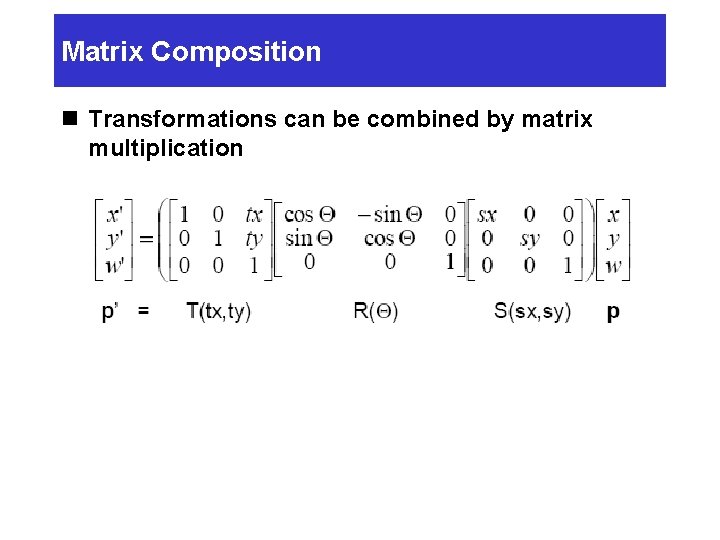
Matrix Composition n Transformations can be combined by matrix multiplication

Matrix Composition n Matrices are a convenient and efficient way to represent a sequence of transformations Ø General purpose representations Ø Hardware matrix multiply Ø Efficiency with premultiplication

Matrix Composition n Be aware: order of transformations matter Ø Matrix multiplication is not commutative “Global” “Local”
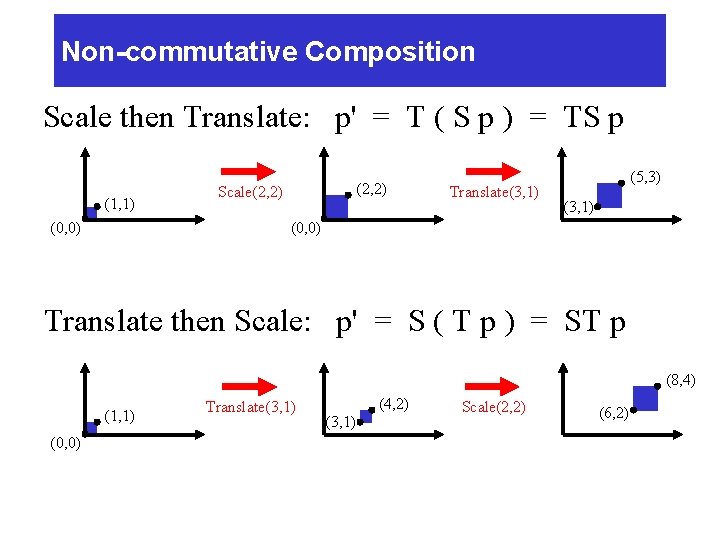
Non-commutative Composition Scale then Translate: p' = T ( S p ) = TS p (1, 1) (2, 2) Scale(2, 2) Translate(3, 1) (5, 3) (3, 1) (0, 0) Translate then Scale: p' = S ( T p ) = ST p (8, 4) (1, 1) (0, 0) Translate(3, 1) (4, 2) (3, 1) Scale(2, 2) (6, 2)
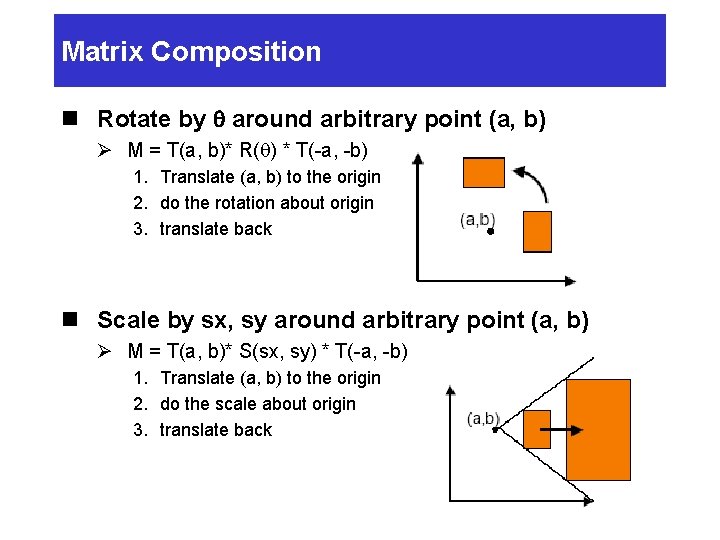
Matrix Composition n Rotate by q around arbitrary point (a, b) Ø M = T(a, b)* R(q) * T(-a, -b) 1. Translate (a, b) to the origin 2. do the rotation about origin 3. translate back n Scale by sx, sy around arbitrary point (a, b) Ø M = T(a, b)* S(sx, sy) * T(-a, -b) 1. Translate (a, b) to the origin 2. do the scale about origin 3. translate back
Transformation Game

Overview n 2 D Transformation Ø Basic 2 D transformations Ø Matrix representation Ø Matrix Composition n 3 D Transformation Ø Basic 3 D transformations Ø Same as 2 D n Transformation Hierarchies Ø Scene graphs Ø Ray casting
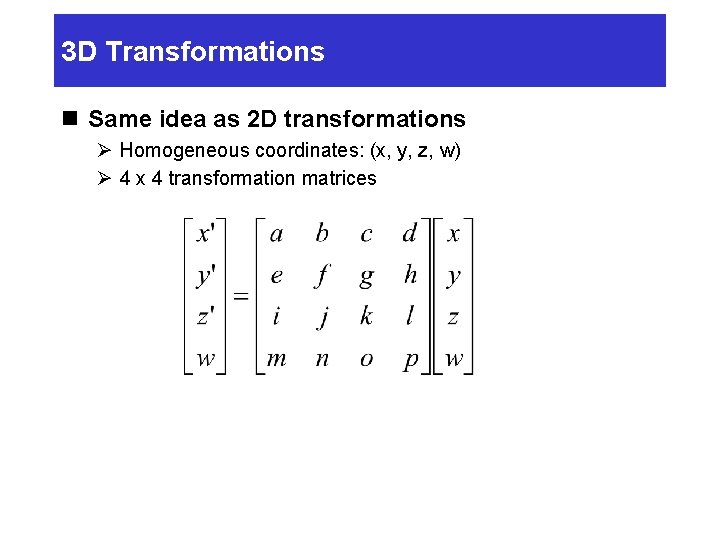
3 D Transformations n Same idea as 2 D transformations Ø Homogeneous coordinates: (x, y, z, w) Ø 4 x 4 transformation matrices
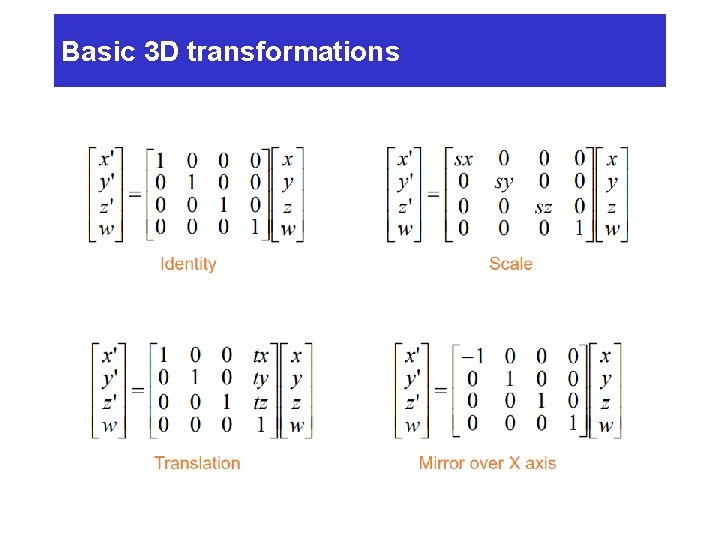
Basic 3 D transformations
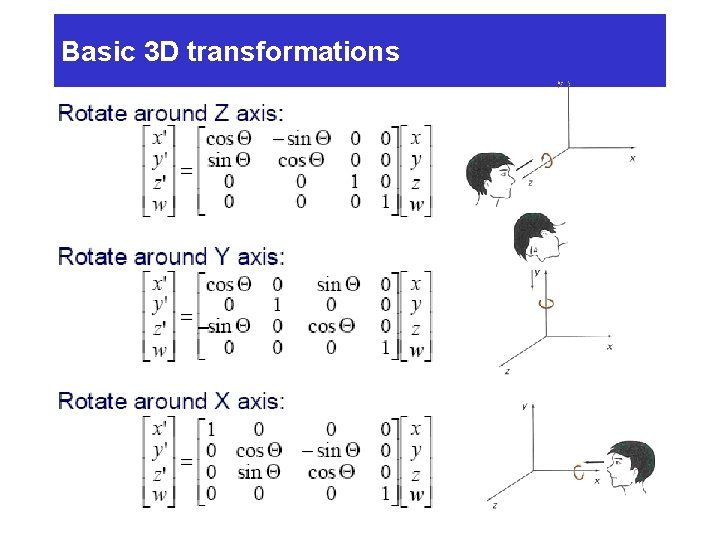
Basic 3 D transformations -
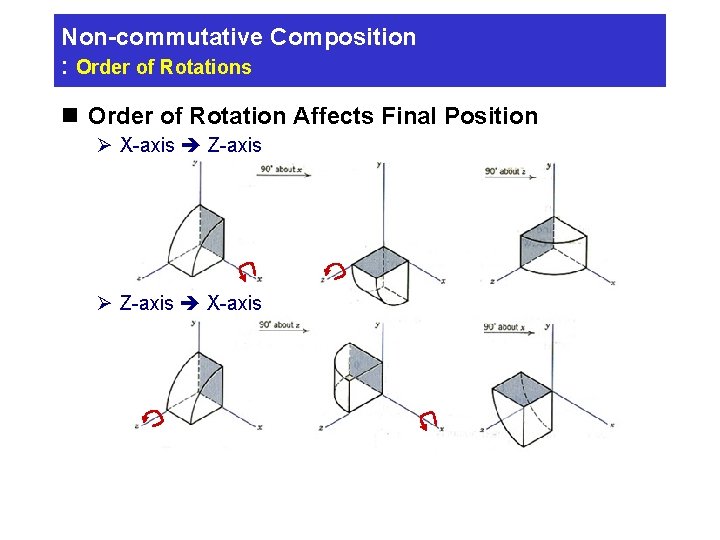
Non-commutative Composition : Order of Rotations n Order of Rotation Affects Final Position Ø X-axis Z-axis Ø Z-axis X-axis

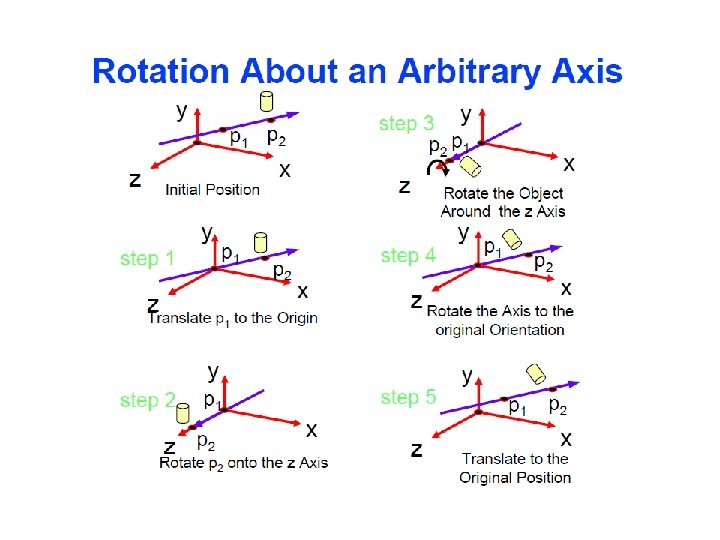
Matrix Composition : Rotations in space n Rotation about an Arbitrary Axis Ø Rotate about some arbitrary a through angle 1. Rotate about the z axis through an angle – The axis a lies in the yz plane 2. Rotate about the x axis through an angle – The axis a coincident with the z axis 3. Rotate about the a axis through – Same as a rotation about the now coincident z axis 4. Reverse the second rotation about the x axis 5. Reverse the first rotation about the z axis – Returning the axis a to its original position z a y x
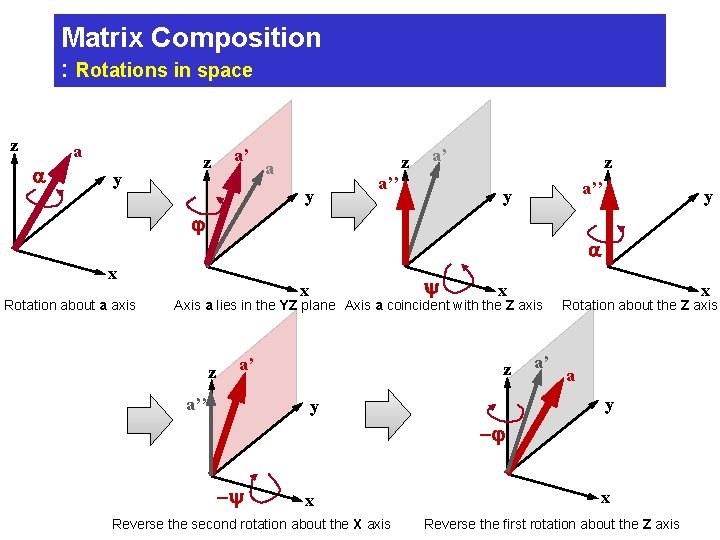
Matrix Composition : Rotations in space z a a y z a’ z a y a’ a’’ z a’’ y y j a x Rotation about a axis y x x Axis a lies in the YZ plane Axis a coincident with the Z axis z a’ a’’ z a’ x Rotation about the Z axis a y y -j -y x Reverse the second rotation about the X axis x Reverse the first rotation about the Z axis
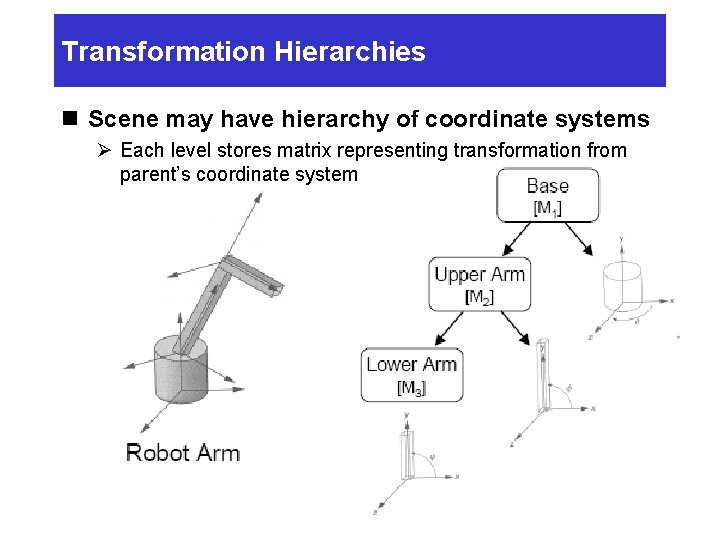
Transformation Hierarchies n Scene may have hierarchy of coordinate systems Ø Each level stores matrix representing transformation from parent’s coordinate system
![Transformation Example 1 Ref] Princeton University Transformation Example 1 Ref] Princeton University](http://slidetodoc.com/presentation_image_h/2e811a46d7e6d1e3ae64fd4d449865e5/image-41.jpg)
Transformation Example 1 Ref] Princeton University
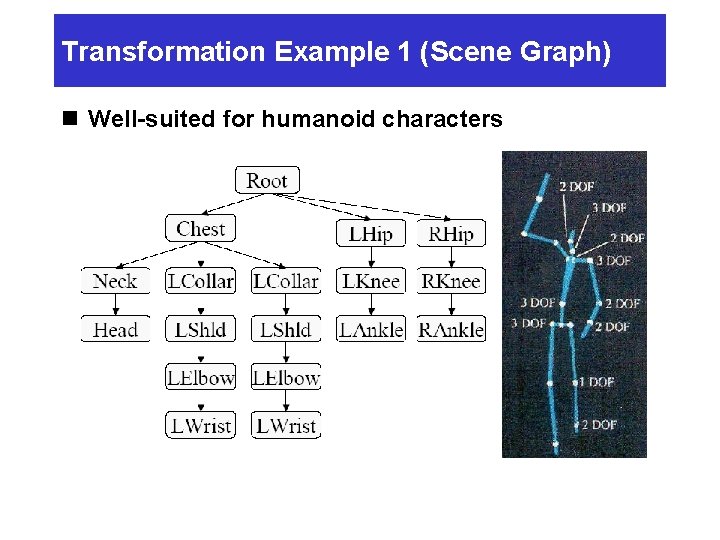
Transformation Example 1 (Scene Graph) n Well-suited for humanoid characters
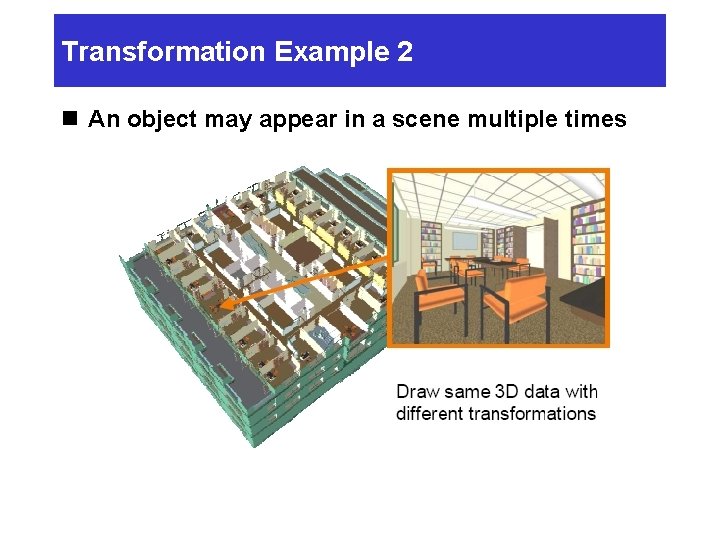
Transformation Example 2 n An object may appear in a scene multiple times
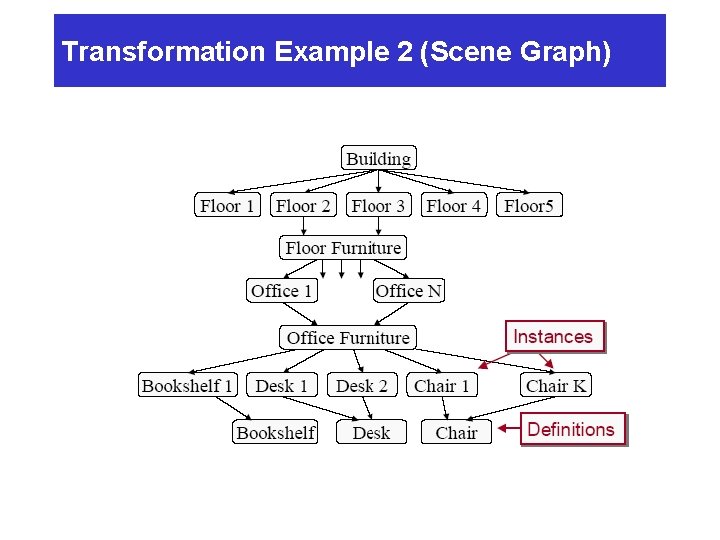
Transformation Example 2 (Scene Graph)

Summary n Coordinate systems Ø World coordinates Ø Modeling coordinates n Representations of 3 D modeling transformations Ø 4 x 4 Matrices • Scale, rotate, translate, shear, projections, etc. • Not arbitrary warps n Composition of 3 D transformations Ø Matrix multiplication (order matters) Ø Transformation hierarchies
- Slides: 45