Modeling the relation between intensity justnoticeable difference and

Modeling the relation between intensity just-noticeable difference and loudness for pure tones and wideband noise J. B. Allen and S. T. Neely J. Acoust. Soc. Am. 102(6): 3628 -4646

Assumptions & concepts • Φ-domain and Ψ-domain variables: intensity and loudness • Fechner: intensity-loudness growth transformation by counting number of loudness JNDs between two intensities • Fletcher’s neural excitation pattern model of loudness • Intensity JND is physical correlate of uncertainty in the loudness

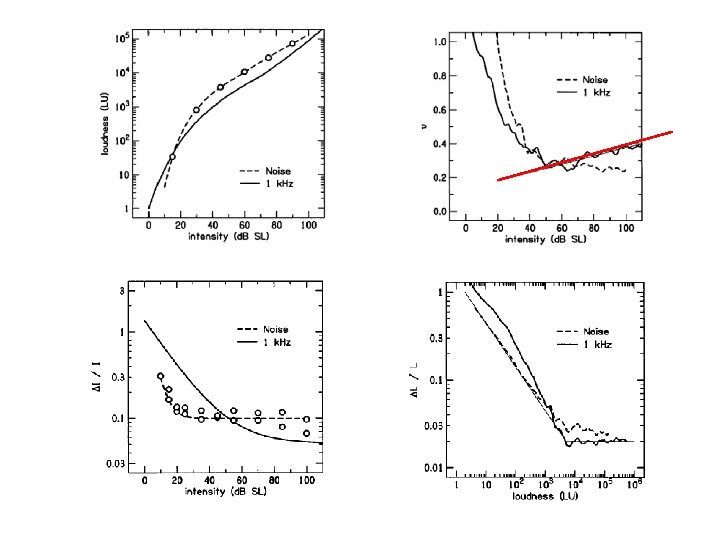
Loudness • Loudness is the Ψ intensity – Depends on stimulus conditions: type of signal, duration, frequency – A loudness scale (e. g. sone) has a reference intensity, frequency, and duration that defines L=1 • A&N introduce single-trial loudness – Mean of single-trial loudness (μL): loudness – Standard deviation of same (σL): loudness JND – μL/σL: SNRL (loudness signal-to-noise ratio) • SNRL(place) is the same for tones and noise!

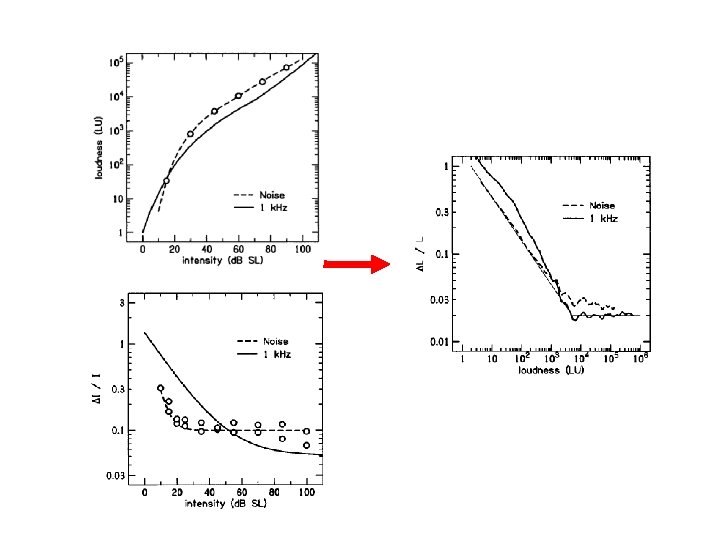
Data used • Tones – Riesz (1928): JND with AM tones – Fletcher and Munson (1933): loudness growth • Wideband noise – Miller (1947): JND and loudness growth

Key ideas used • Fechner: loudness growth function can be obtained by counting JNDs • Fletcher: sum of neural spike rate determines loudness • Siebert: loudness JND is determined by Poisson noise • Hellmann and Hellmann: – Poisson Internal Noise model – Relation between intensity- and loudness-JND via loudness growth function

Definitions • Intensity of masker + probe • Intensity JND (masker = scaled probe) • Signal detection theory

Derived definitions (1) • Weber fraction • Loudness JND (small-JND approximation) • Loudness SNR assuming that

Derived definitions (2) • Counting JNDs (Fechner) The number of JNDs must be the same regardless of the domain

Weber’s Law • J is independent of I – Not true for pure tones (“near miss to Weber’s Law”) – True for wideband noise Weber’s Law is “approximately” true

Fechner’s Postulate • ΔL is constant Fechner JND counting formula • Marry Weber and Fechner Weber-Fechner Law Fechner’s Postulate is not true, so the Weber-Fechner Law is also not true

Poisson noise • Neural spike count determines loudness • Spike rate is a Poisson process • Poisson noise determines loudness JND Poisson Internal Noise PIN model

PIN model • Hellmann and Hellman (1990) propose based on PIN model PIN JND counting formula

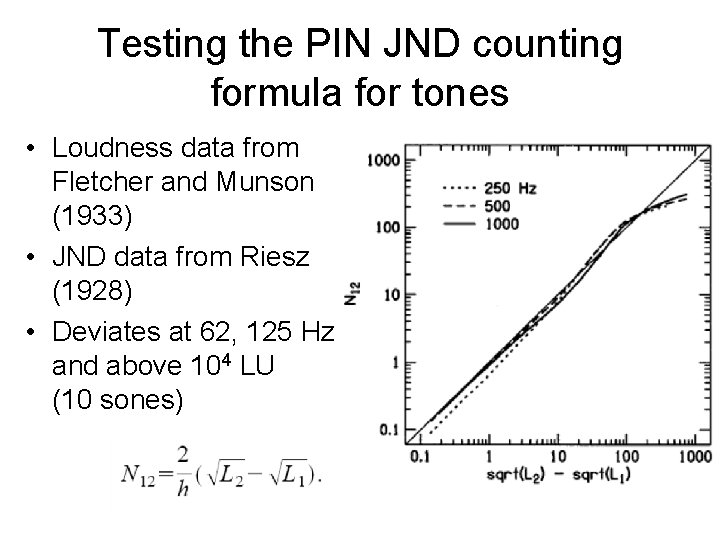
Testing the PIN JND counting formula for tones • Loudness data from Fletcher and Munson (1933) • JND data from Riesz (1928) • Deviates at 62, 125 Hz and above 104 LU (10 sones)

Single-trial loudness with PIN • The PIN model is consistent with • Because we get i. e. , the mean of the single-trial loudness L is proportional to the variance of the single -trial loudness This is what we would expect for a Poisson process, consistent with Siebert

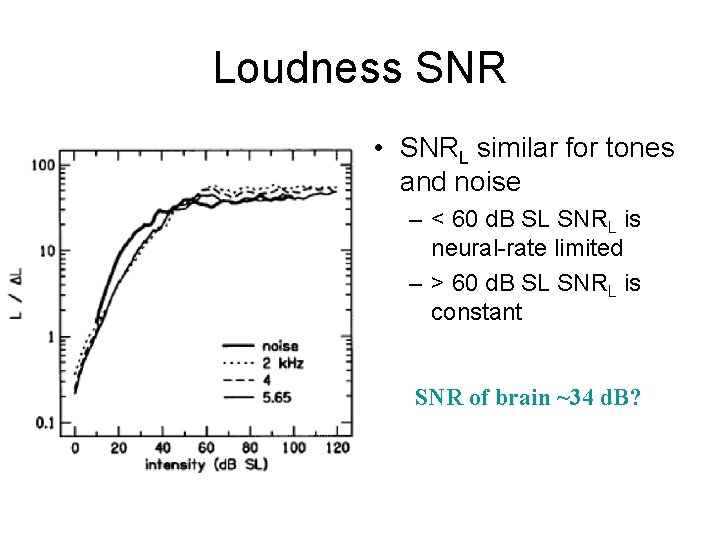
Loudness SNR • SNRL similar for tones and noise – < 60 d. B SL SNRL is neural-rate limited – > 60 d. B SL SNRL is constant SNR of brain ~34 d. B?

SPIN model • Summary equation for ΔL/L Saturated Poisson Internal Noise model • Use SPIN model to derive Weber fraction

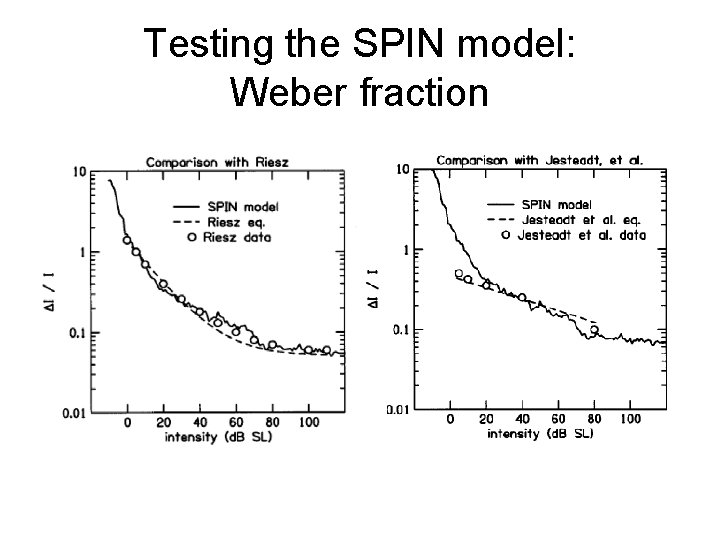
Testing the SPIN model: Weber fraction

Model of loudness coding • Fletcher’s neural excitation pattern model proposed that summation of total spike activity accounts for loudness • Since neural discharge is a Poisson process, Fletcher’s model predicts loudness JND for tones and noise (up to about 60 d. B SL)

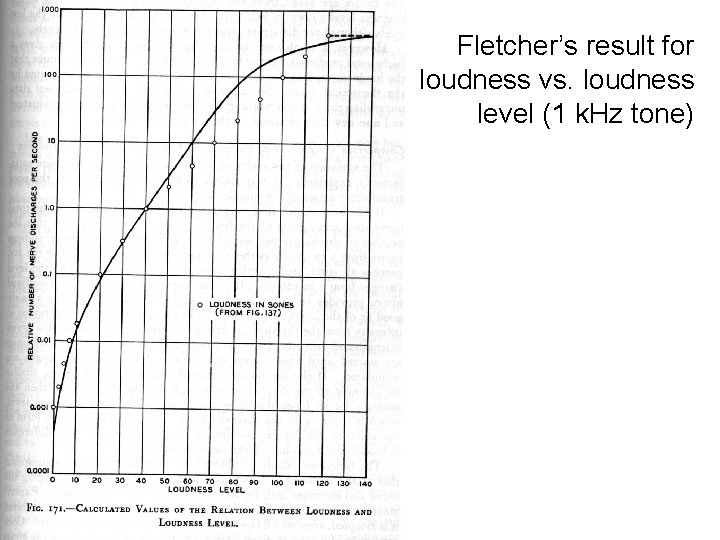
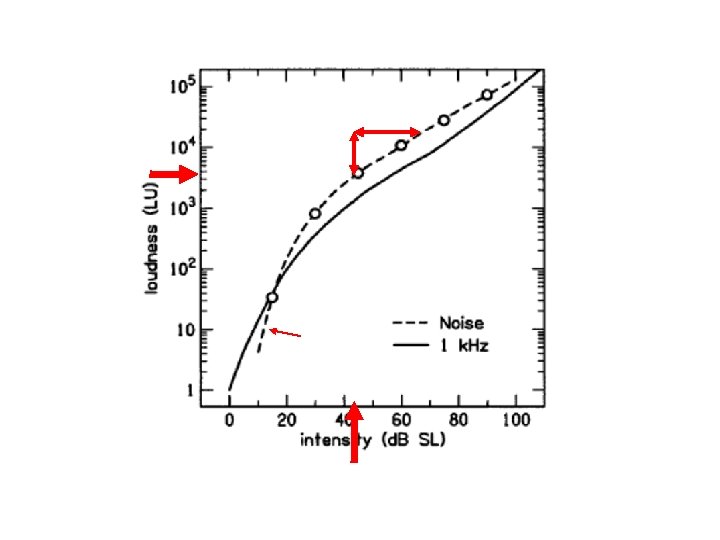
Fletcher’s result for loudness vs. loudness level (1 k. Hz tone)