Modeling Techniques Deterministic A deterministic model is one



- Slides: 8

Modeling Techniques Deterministic : A deterministic model is one in which every set of variable states is uniquely determined by parameters in the model and by sets of previous states of these variables Probabilistic or Stochastic: In probabilistic model, randomness is present, and variable states are not described by unique values, but rather by probability distributions. Markov process is commonly used probabilistic technique.

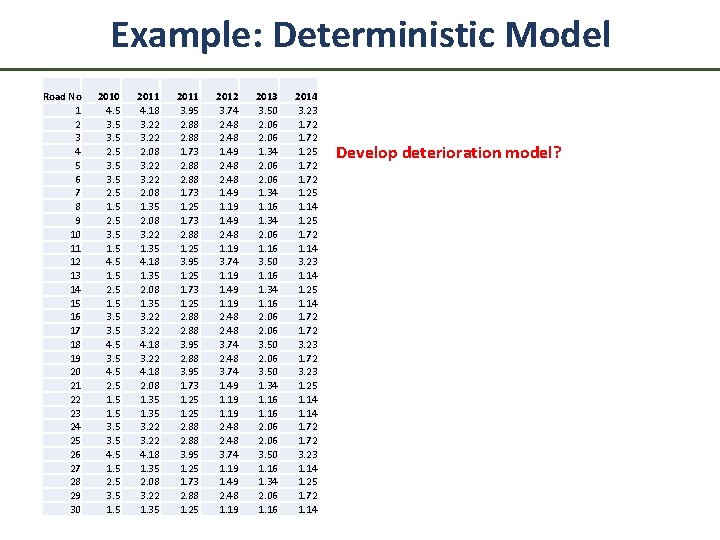
Example: Deterministic Model Road No 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 2010 4. 5 3. 5 2. 5 1. 5 2. 5 3. 5 1. 5 4. 5 1. 5 2. 5 1. 5 3. 5 4. 5 1. 5 2. 5 3. 5 1. 5 2011 4. 18 3. 22 2. 08 1. 35 2. 08 3. 22 1. 35 4. 18 1. 35 2. 08 1. 35 3. 22 4. 18 2. 08 1. 35 3. 22 4. 18 1. 35 2. 08 3. 22 1. 35 2011 3. 95 2. 88 1. 73 1. 25 1. 73 2. 88 1. 25 3. 95 1. 25 1. 73 1. 25 2. 88 3. 95 1. 25 1. 73 2. 88 1. 25 2012 3. 74 2. 48 1. 49 1. 19 1. 49 2. 48 1. 19 3. 74 1. 19 1. 49 1. 19 2. 48 3. 74 1. 19 1. 49 2. 48 1. 19 2013 3. 50 2. 06 1. 34 1. 16 1. 34 2. 06 1. 16 3. 50 1. 16 1. 34 1. 16 2. 06 3. 50 1. 16 1. 34 2. 06 1. 16 2014 3. 23 1. 72 1. 25 1. 14 1. 25 1. 72 1. 14 3. 23 1. 14 1. 25 1. 14 1. 72 3. 23 1. 14 1. 25 1. 72 1. 14 Develop deterioration model?

Markovian Probabilistic Process Step 1: Summary Database Step 2: Transition Matrix Step 3: Transition Probability Matrix

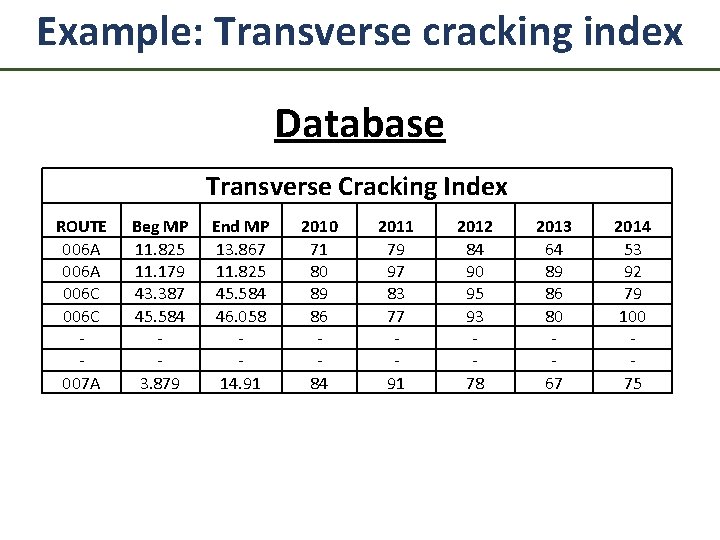
Example: Transverse cracking index Database Transverse Cracking Index ROUTE 006 A 006 C 007 A Beg MP 11. 825 11. 179 43. 387 45. 584 3. 879 End MP 13. 867 11. 825 45. 584 46. 058 14. 91 2010 71 80 89 86 84 2011 79 97 83 77 91 2012 84 90 95 93 78 2013 64 89 86 80 67 2014 53 92 79 100 75

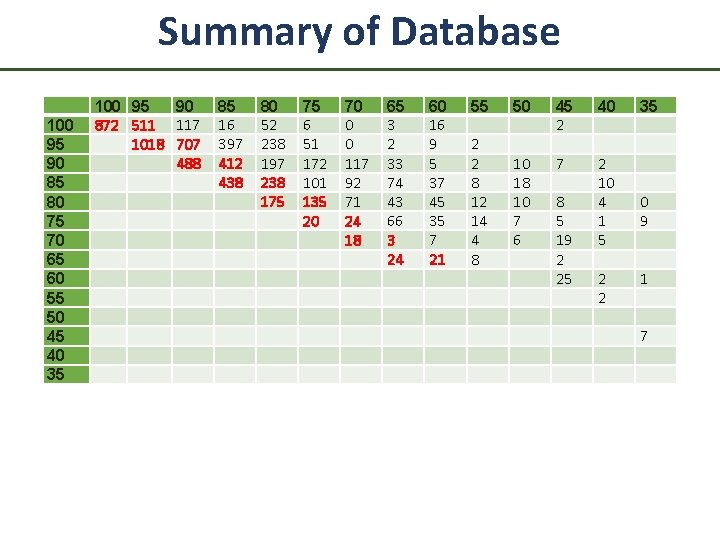
Summary of Database 100 95 90 85 80 75 70 65 60 55 50 45 40 35 100 95 90 872 511 117 1018 707 488 85 16 397 412 438 80 52 238 197 238 175 75 6 51 172 101 135 20 70 0 0 117 92 71 24 18 65 3 2 33 74 43 66 3 24 60 16 9 5 37 45 35 7 21 55 50 40 2 2 8 12 14 4 8 45 2 10 18 10 7 6 7 2 10 4 1 5 8 5 19 2 25 2 2 35 0 9 1 7

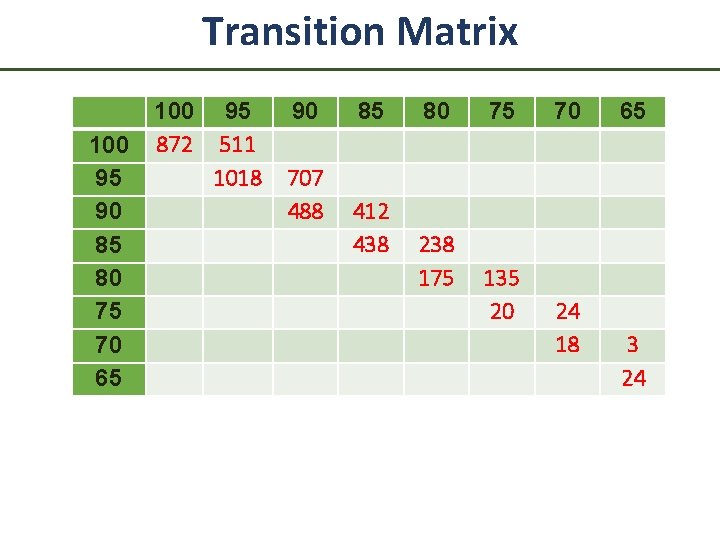
Transition Matrix 100 95 90 85 80 75 70 65 100 872 95 511 1018 90 707 488 85 412 438 80 238 175 75 135 20 70 24 18 65 3 24

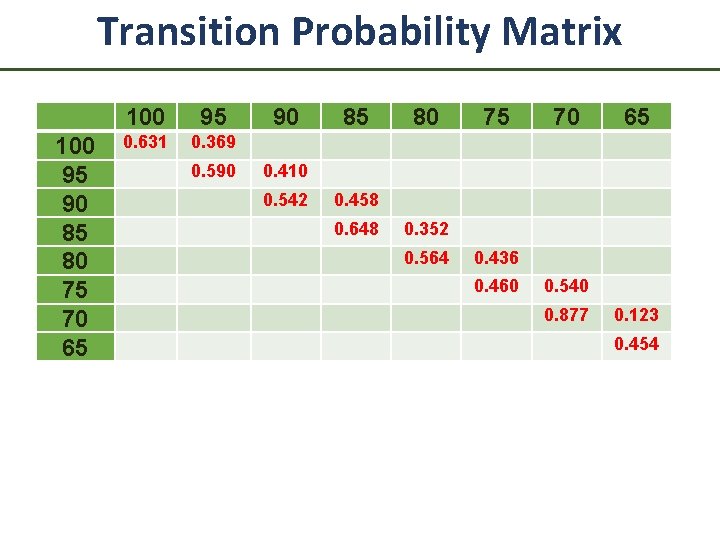
Transition Probability Matrix 100 95 90 85 80 75 70 65 100 95 0. 631 0. 369 0. 590 90 85 80 75 70 65 0. 410 0. 542 0. 458 0. 648 0. 352 0. 564 0. 436 0. 460 0. 540 0. 877 0. 123 0. 454
