Modeling Student Benefits from Illustrations and Graphs Michael

Modeling Student Benefits from Illustrations and Graphs Michael Lipschultz Diane Litman Intelligent Tutoring Systems Conference (2014)

Motivation • Best representation varies – Gender – Knowledge – Skills • Identify situations when illustrations or graphs improved learning gains – Future: adapt to students/situations 2

Data • Prior study – Problem-solving + post-problem discussion – Saw either illustrations only or graphs only – Pretest & Post-test – to measure learning gains – 29 subjects: 2, 042 data points • Features: – Student information] – Student skill – Domain information – Contextual information 3

Modeling with Stepwise Regression 1. Stepwise Linear Regression • Postscore = terms + prescore • terms: representation*(tutoring context) representation*partition*rule – Illustration*(Pre. Score=High)*(Response. Time=Fast) – For high pretesters, when Response. Time=Fast, show illustrations – Binary features • Keeps only predictive terms 4

Modeling with Stepwise Regression Algorithm 1. Stepwise Linear Regression 2. Identify Problematic Rules – (Potentially) Mutually Exclusive – Non-Adaptive 3. Handle Problematic Rules – Remove Lesser Rule in Pair 4. Relearn Model – Regular Regression 5

Modeling the Best Representation: Experiment • Model Types – Baseline: just show one kind (illustration) – 1 Factor: 1 Tutoring Context factor in term – 2 Factors: Partition data along 1 variable • High pretesters vs. Low pretesters – 3 Factors: Partition along 2 variables 6

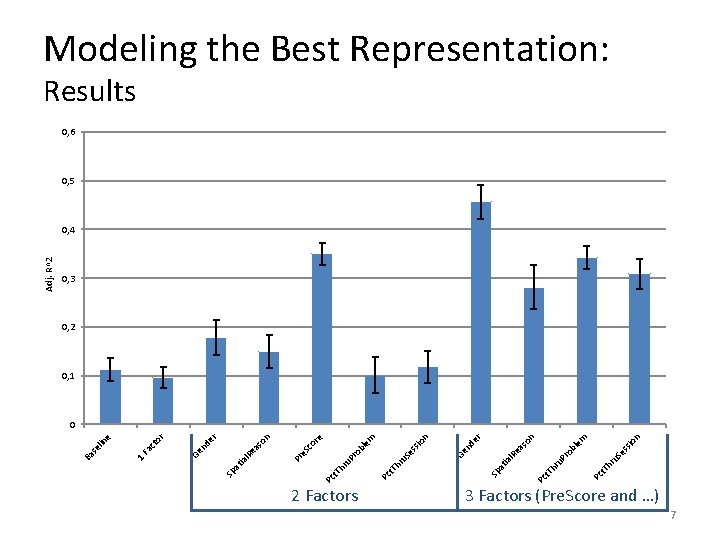
2 Factors n n ss io em bl ro hr u. S e t. T Pc u. P Pc t. T hr so ea l. R ia Sp at nd er n ss io Ge e em bl ro hr u. S e t. T Pc u. P Pc t. T hr co r e. S Pr n so ea l. R ia Sp at nd er r ct o Fa Ge 1 in e se l Ba Adj. R^2 Modeling the Best Representation: Results 0, 6 0, 5 0, 4 0, 3 0, 2 0, 1 0 3 Factors (Pre. Score and …) 7

Modeling the Best Representation: Pre. Score Model High Pretesters (n=11) Low Pretesters (n=18) 1. If few correct answers during walk throughs or reflection dialogues, show graphs 2. If many correct answers during session, show illustrations 3. If later in tutoring, show illustrations 4. If few correct answers in problem, show graphs 1. If many correct answers during session, show illustrations 2. If few correct answers in problem, show illustrations 3. If later in tutoring, show illustrations 8

Interpreting the Model Pre. Score*Gender Females (n=8) High Pretesters 1. If few correct answers in walk throughs or reflections, show graphs 2. If many correct answers in session or problem, show illustrations 3. If early in problem or session, show graphs (n=9) Low Pretesters 1. If many correct answers in session, show graphs 2. If early in session, show illustrations 3. If many correct answers in problem, show illustrations 4. If early in problem, show illustrations 5. If few correct answers in reflections, show illustrations Males (n=3) 1. If few correct in reflections, show illustrations 2. If many correct in session, show illustrations 3. If few correct in walk throughs, show illustrations (n=9) 1. If few correct answers in walk throughs or reflections, show illustrations 2. If many correct answers in session, show illustrations 3. If early in session or problem, show graphs 4. If many correct answers in problem, show illustrations 9

Conclusion • Developed modeling technique – Unknown gold standard – Handles “problematic” rules • 5 models outperform baseline – Possible to model benefit • Partitioning Useful: Pre. Score & Gender 10

Future Work • Empirical Evaluation of Model – currently working on – Is adapting visual representation helpful? • Develop method of selecting partition features – Partial correlation with postscore (covars=existing partitions)? • Does modeling algorithm transfer to other tasks? • Compare performance to Reinforcement Learning 11

Thank you